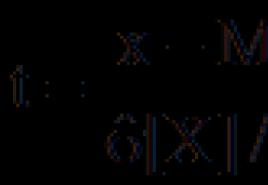Kā paplašināt kubu summu. Saīsinātās reizināšanas formulas

Iepriekšējās nodarbībās mēs apsvērām divus veidus, kā faktorizēt polinomu: kopējā faktora izņemšanu no iekavām un grupēšanas metodi.

Šajā nodarbībā mēs aplūkosim citu veidu, kā faktorizēt polinomu izmantojot saīsinātās reizināšanas formulas.

Mēs iesakām katru formulu uzrakstīt vismaz 12 reizes. Lai labāk iegaumētu, pierakstiet sev visas saīsinātās reizināšanas formulas uz mazas krāpšanās lapas.

Atgādiniet, kā izskatās kubu atšķirības formula.

a 3 − b 3 = (a − b) (a 2 + ab + b 2)

Kubu atšķirības formulu nav ļoti viegli atcerēties, tāpēc iesakām izmantot īpašu veidu, kā to atcerēties.

Ir svarīgi saprast, ka darbojas arī jebkura saīsināta reizināšanas formula otrā puse.

(a – b) (a 2 + ab + b 2) = a 3 - b 3

Apsveriet piemēru. Ir nepieciešams faktorizēt kubu starpību.

Ņemiet vērā, ka "27a 3" ir "(3a) 3", kas nozīmē, ka kubu starpības formulai "a" vietā mēs izmantojam "3a".

Mēs izmantojam kubu atšķirības formulu. “a 3” vietā mums ir “27a 3”, un “b 3” vietā, kā formulā, ir “b 3”.

Kuba starpības piemērošana apgrieztā veidā

Apskatīsim citu piemēru. Polinomu reizinājums ir jāpārvērš kubu starpībā, izmantojot saīsināto reizināšanas formulu.

Lūdzu, ņemiet vērā, ka polinomu reizinājums “(x − 1) (x 2 + x + 1)” atgādina kubu starpības formulas labo pusi, tikai “a” vietā ir “x”, un "b" vieta ir "1".

Attiecībā uz “(x − 1)(x 2 + x + 1)” mēs izmantojam formulu kubu atšķirībai pretējā virzienā.

Apskatīsim sarežģītāku piemēru. Ir nepieciešams vienkāršot polinomu reizinājumu.

Ja salīdzinām "(y 2 − 1)(y 4 + y 2 + 1)" ar kubu starpības formulas labo pusi
« a 3 − b 3 = (a − b) (a 2 + ab + b 2)”, tad jūs varat saprast, ka “a” vietā no pirmās iekavas ir “y 2”, bet “b” vietā ir “1”.

Saīsinātās reizināšanas formulas (FSU) tiek izmantotas skaitļu un izteiksmju paaugstināšanai un reizināšanai. Bieži vien šīs formulas ļauj veikt aprēķinus kompaktāk un ātrāk.

Šajā rakstā mēs uzskaitīsim galvenās saīsinātās reizināšanas formulas, sagrupēsim tās tabulā, apsvērsim šo formulu izmantošanas piemērus, kā arī pakavēsimies pie saīsināto reizināšanas formulu pierādīšanas principiem.

Pirmo reizi FSU tēma tiek aplūkota kursa "Algebra" ietvaros 7. klasei. Zemāk ir 7 pamata formulas.

Saīsinātās reizināšanas formulas

1. summas kvadrāta formula: a + b 2 = a 2 + 2 a b + b 2
2. starpības kvadrātveida formula: a - b 2 \u003d a 2 - 2 a b + b 2
3. summas kuba formula: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
4. atšķirības kuba formula: a - b 3 \u003d a 3 - 3 a 2 b + 3 a b 2 - b 3
5. kvadrātu atšķirības formula: a 2 - b 2 \u003d a - b a + b
6. kubu summas formula: a 3 + b 3 \u003d a + b a 2 - a b + b 2
7. kuba starpības formula: a 3 - b 3 \u003d a - b a 2 + a b + b 2

Burti a, b, c šajās izteiksmēs var būt jebkuri cipari, mainīgie vai izteiksmes. Lietošanas ērtībai septiņas pamatformulas labāk iemācīties no galvas. Mēs tos apkopojam tabulā un sniedzam tālāk, apvelkot tos ar lodziņu.

Pirmās četras formulas ļauj aprēķināt attiecīgi divu izteiksmju summas vai starpības kvadrātu vai kubu.

Piektā formula aprēķina izteiksmju kvadrātu starpību, reizinot to summu un starpību.

Sestā un septītā formula ir attiecīgi izteiksmju summas un starpības reizinājums ar starpības nepilno kvadrātu un summas nepilnīgo kvadrātu.

Saīsināto reizināšanas formulu dažreiz sauc arī par saīsinātajām reizināšanas identitātēm. Tas nav pārsteidzoši, jo katra vienlīdzība ir identitāte.

Izlemjot praktiski piemēri bieži izmanto saīsinātas reizināšanas formulas ar pārkārtotām kreiso un labo daļu. Tas ir īpaši ērti, ja tiek ņemts vērā polinoms.

Papildu saīsinātās reizināšanas formulas

Mēs neaprobežosimies tikai ar 7. klases kursu algebrā un pievienosim vēl dažas formulas mūsu FSU tabulai.

Pirmkārt, apsveriet Ņūtona binominālo formulu.

a + b n = C n 0 a n + C n 1 a n - 1 b + C n 2 a n - 2 b 2 + . . + C n n - 1 a b n - 1 + C n n b n

Šeit C n k ir binomiālie koeficienti, kas atrodas Paskāla trijstūra rindā n. Binomiālos koeficientus aprēķina pēc formulas:

C nk = n ! k! · (n - k) ! = n (n - 1) (n - 2) . . (n - (k - 1)) k !

Kā redzat, starpības un summas kvadrāta un kuba FSU ir īpašs Ņūtona binominālās formulas gadījums attiecīgi n=2 un n=3.

Bet ko darīt, ja summā ir vairāk nekā divi termini, kas jāpaaugstina līdz pakāpēm? Noderēs trīs, četru vai vairāk terminu summas kvadrāta formula.

a 1 + a 2 +. . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n - 1 a n

Vēl viena formula, kas var noderēt, ir divu terminu n-tās pakāpes atšķirības formula.

a n - b n = a - b a n - 1 + a n - 2 b + a n - 3 b 2 + . . + a 2 b n - 2 + b n - 1

Šo formulu parasti iedala divās formulās – attiecīgi pāra un nepāra grādiem.

Pāra eksponentiem 2m:

a 2 m - b 2 m = a 2 - b 2 a 2 m - 2 + a 2 m - 4 b 2 + a 2 m - 6 b 4 + . . + b 2 m - 2

Nepāra eksponentiem 2m+1:

a 2 m + 1 - b 2 m + 1 = a 2 - b 2 a 2 m + a 2 m - 1 b + a 2 m - 2 b 2 + . . + b 2 m

Formulas kvadrātu atšķirībai un kubu atšķirībai, jūs uzminējāt, ir šīs formulas īpašie gadījumi attiecīgi n = 2 un n = 3. Kubu starpībai b arī tiek aizstāts ar - b .

Kā lasīt saīsinātās reizināšanas formulas?

Katrai formulai dosim atbilstošos formulējumus, bet vispirms apskatīsim formulu lasīšanas principu. Vienkāršākais veids, kā to izdarīt, ir izmantot piemēru. Ņemsim pašu pirmo formulu divu skaitļu summas kvadrātam.

a + b 2 = a 2 + 2 a b + b 2 .

Viņi saka: divu izteiksmju a un b summas kvadrāts ir vienāds ar pirmās izteiksmes kvadrāta summu, divreiz izteiksmju reizinājumu un otrās izteiksmes kvadrātu.

Visas pārējās formulas tiek lasītas līdzīgi. Kvadrātveida starpībai a - b 2 \u003d a 2 - 2 a b + b 2 mēs rakstām:

divu izteiksmju a un b starpības kvadrāts ir vienāds ar šo izteiksmju kvadrātu summu, no kuras atņemtas divkāršs pirmās un otrās izteiksmes reizinājums.

Nolasīsim formulu a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3. Divu izteiksmju a un b summas kubs ir vienāds ar šo izteiksmju kubu summu, trīs reizes ar pirmās un otrās izteiksmes kvadrāta reizinājumu un trīs reizes ar otrās izteiksmes kvadrāta reizinājumu. un pirmā izteiksme.

Mēs turpinām lasīt kubu atšķirības formulu a - b 3 \u003d a 3 - 3 a 2 b + 3 a b 2 - b 3. Divu izteiksmju a un b starpības kubs ir vienāds ar pirmās izteiksmes kubu mīnus trīs reizes pirmās izteiksmes un otrās izteiksmes kvadrāts, plus trīs reizes otrās izteiksmes un pirmās izteiksmes kvadrāts, atskaitot kubu no otrās izteiksmes.

Piektā formula a 2 - b 2 \u003d a - b a + b (kvadrātu starpība) skan šādi: divu izteiksmju kvadrātu starpība ir vienāda ar starpības un abu izteiksmju summas reizinājumu.

Ērtības labad tādas izteiksmes kā a 2 + a b + b 2 un a 2 - a b + b 2 attiecīgi sauc par summas nepilno kvadrātu un starpības nepilno kvadrātu.

Paturot to prātā, kubu summas un starpības formulas tiek lasītas šādi:

Divu izteiksmju kubu summa ir vienāda ar šo izteiksmju summas un to starpības nepilnā kvadrāta reizinājumu.

Divu izteiksmju kubu starpība ir vienāda ar šo izteiksmju starpības reizinājumu ar to summas nepilno kvadrātu.

FSU pierādījums

FSU pierādīšana ir pavisam vienkārša. Pamatojoties uz reizināšanas īpašībām, mēs veiksim iekavās esošo formulu daļu reizināšanu.

Piemēram, apsveriet starpības kvadrāta formulu.

a - b 2 \u003d a 2 - 2 a b + b 2.

Lai izteiksmi paaugstinātu līdz otrajai pakāpei, izteiksme ir jāreizina pati ar sevi.

a - b 2 \u003d a - b a - b.

Izvērsīsim iekavas:

a - b a - b \u003d a 2 - a b - b a + b 2 \u003d a 2 - 2 a b + b 2.

Formula ir pierādīta. Pārējie FSO ir pierādīti līdzīgi.

FSO pielietojuma piemēri

Saīsināto reizināšanas formulu izmantošanas mērķis ir ātri un īsa reizināšana un izteicienu paaugstināšana līdz pilnvarām. Tomēr tā nav visa FSO darbības joma. Tos plaši izmanto izteiksmju samazināšanai, daļskaitļu samazināšanai, polinomu faktoringam. Sniegsim piemērus.

Piemērs 1. FSO

Vienkāršosim izteiksmi 9 y - (1 + 3 y) 2 .

Pielietojiet kvadrātu summas formulu un iegūstiet:

9 g - (1 + 3 g) 2 = 9 g - (1 + 6 g + 9 g 2) = 9 g - 1 - 6 g - 9 g 2 = 3 g - 1 - 9 g 2

2. piemērs. FSO

Samaziniet daļu 8 x 3 - z 6 4 x 2 - z 4 .

Mēs pamanām, ka izteiksme skaitītājā ir kubu starpība, bet saucējā - kvadrātu atšķirība.

8 x 3 - z 6 4 x 2 - z 4 \u003d 2 x - z (4 x 2 + 2 x z + z 4) 2 x - z 2 x + z.

Mēs samazinām un iegūstam:

8 x 3 - z 6 4 x 2 - z 4 = (4 x 2 + 2 x z + z 4) 2 x + z

FSU palīdz arī aprēķināt izteiksmju vērtības. Galvenais ir prast pamanīt, kur piemērot formulu. Parādīsim to ar piemēru.

Apvienosim kvadrātā skaitli 79. Apgrūtinošu aprēķinu vietā mēs rakstām:

79 = 80 - 1 ; 79 2 = 80 - 1 2 = 6400 - 160 + 1 = 6241 .

Šķiet, ka sarežģīts aprēķins tika veikts ātri, izmantojot tikai saīsinātas reizināšanas formulas un reizināšanas tabulu.

Cits svarīgs punkts- binoma kvadrāta izvēle. Izteiksmi 4 x 2 + 4 x - 3 var pārvērst par 2 x 2 + 2 2 x 1 + 1 2 - 4 = 2 x + 1 2 - 4 . Šādas transformācijas tiek plaši izmantotas integrācijā.

Ja pamanāt tekstā kļūdu, lūdzu, iezīmējiet to un nospiediet Ctrl+Enter

Saīsinātās reizināšanas formulas.

Saīsinātās reizināšanas formulu izpēte: summas kvadrāts un divu izteiksmju starpības kvadrāts; divu izteiksmju kvadrātu atšķirība; divu izteiksmju summas kubs un starpības kubs; divu izteiksmju kubu summas un atšķirības.

Saīsināto reizināšanas formulu pielietojums, risinot piemērus.

Lai vienkāršotu izteiksmes, faktorizētu polinomus un samazinātu polinomus līdz standarta formai, tiek izmantotas saīsinātas reizināšanas formulas. Saīsinātās reizināšanas formulas, kas jāzina no galvas.

Ļaujiet a, b R. Tad:

1. Divu izteiksmju summas kvadrāts ir pirmās izteiksmes kvadrāts plus divkāršs pirmās izteiksmes reizinājums un otrais plus otrās izteiksmes kvadrāts.

(a + b) 2 = a 2 + 2ab + b 2

2. Divu izteiksmju starpības kvadrāts ir pirmās izteiksmes kvadrāts mīnus divreiz pirmās izteiksmes reizinājums un otrais plus otrās izteiksmes kvadrāts.

(a - b) 2 = a 2 - 2ab + b 2

3. Kvadrātu atšķirība divas izteiksmes ir vienādas ar šo izteiksmju un to summas starpības reizinājumu.

a 2 - b 2 \u003d (a - b) (a + b)

4. summas kubs no divām izteiksmēm ir vienāds ar pirmās izteiksmes kubu plus trīs reizes pirmās izteiksmes kvadrāts reizināts ar otro plus trīs reizes pirmās izteiksmes reizinājums ar otrās izteiksmes kvadrātu plus otrās izteiksmes kubs.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. atšķirības kubs no divām izteiksmēm ir vienāds ar pirmās izteiksmes kubu, no kura trīs reizes atņemts pirmās izteiksmes kvadrāta reizinājums un otrās plus trīs reizes pirmās izteiksmes reizinājums un otrās izteiksmes kvadrāts mīnus otrās izteiksmes kubs.

(a - b) 3 = a 3 - 3a 2 b + 3ab 2 - b 3

6. Kubu summa divas izteiksmes ir vienādas ar pirmās un otrās izteiksmes summas reizinājumu ar šo izteiksmju starpības nepilno kvadrātu.

a 3 + b 3 \u003d (a + b) (a 2 - ab + b 2)

7. Kubu atšķirība no divām izteiksmēm ir vienāds ar pirmās un otrās izteiksmes starpības reizinājumu ar šo izteiksmju summas nepilno kvadrātu.

a 3 - b 3 \u003d (a - b) (a 2 + ab + b 2)

Saīsināto reizināšanas formulu pielietojums, risinot piemērus.

1. piemērs

Aprēķināt

a) Izmantojot formulu divu izteiksmju summas kvadrātam, mēs iegūstam

(40+1) 2 = 40 2 + 2 40 1 + 1 2 = 1600 + 80 + 1 = 1681

b) Izmantojot formulu divu izteiksmju starpības kvadrātā, iegūstam

98 2 \u003d (100 - 2) 2 \u003d 100 2 - 2 100 2 + 2 2 \u003d 10000 - 400 + 4 = 9604

2. piemērs

Aprēķināt

Izmantojot formulu divu izteiksmju kvadrātu starpībai, iegūstam

3. piemērs

Vienkāršojiet izteiksmi

(x - y) 2 + (x + y) 2

Mēs izmantojam formulas summas kvadrātam un divu izteiksmju starpības kvadrātam

(x - y) 2 + (x + y) 2 \u003d x 2 - 2xy + y 2 + x 2 + 2xy + y 2 \u003d 2x 2 + 2y 2

Saīsinātās reizināšanas formulas vienā tabulā:

(a + b) 2 = a 2 + 2ab + b 2
(a - b) 2 = a 2 - 2ab + b 2
a 2 - b 2 = (a - b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a - b) 3 = a 3 - 3a 2 b + 3ab 2 - b 3
a 3 + b 3 \u003d (a + b) (a 2 - ab + b 2)
a 3 - b 3 \u003d (a - b) (a 2 + ab + b 2)

Kvadrātu atšķirība

Mēs iegūstam kvadrātu $a^2-b^2$ atšķirības formulu.

Lai to izdarītu, atcerieties šādu noteikumu:

Ja izteiksmei pievieno jebkuru monomu un atņem to pašu monomu, tad iegūstam pareizo identitāti.

Pievienosim izteiksmei un atņemsim no tās monomu $ab$:

Kopumā mēs iegūstam:

Tas ir, divu monomālu kvadrātu starpība ir vienāda ar to starpības un summas reizinājumu.

1. piemērs

Izteikt kā $(4x)^2-y^2$ reizinājumu

\[(4x)^2-y^2=((2x))^2-y^2\]

\[((2x))^2-y^2=\kreisais(2x-y\labais)(2x+y)\]

Kubu summa

Mēs iegūstam formulu kubu summai $a^3+b^3$.

Izņemsim no iekavām izplatītākos faktorus:

Izņemsim $\left(a+b\right)$ no iekavām:

Kopumā mēs iegūstam:

Tas nozīmē, ka divu monomālu kubu summa ir vienāda ar to summas reizinājumu ar to starpības nepilno kvadrātu.

2. piemērs

Izteikt kā produktu $(8x)^3+y^3$

Šo izteiksmi var pārrakstīt šādā formā:

\[(8x)^3+y^3=((2x))^3+y^3\]

Izmantojot kvadrātu starpības formulu, mēs iegūstam:

\[((2x))^3+y^3=\left(2x+y\right)(4x^2-2xy+y^2)\]

Kubu atšķirība

Mēs iegūstam kubu atšķirības formulu $a^3-b^3$.

Lai to izdarītu, mēs izmantosim to pašu noteikumu, kas minēts iepriekš.

Pievienosim izteiksmei un atņemsim no tās monomālus $a^2b\ un\ (ab)^2$:

Izņemsim no iekavām izplatītākos faktorus:

Izņemsim $\left(a-b\right)$ no iekavām:

Kopumā mēs iegūstam:

Tas ir, divu monomālu kubu starpība ir vienāda ar to starpības reizinājumu ar to summas nepilno kvadrātu.

3. piemērs

Izteikt kā $(8x)^3-y^3$ reizinājumu

Šo izteiksmi var pārrakstīt šādā formā:

\[(8x)^3-y^3=((2x))^3-y^3\]

Izmantojot kvadrātu starpības formulu, mēs iegūstam:

\[((2x))^3-y^3=\kreisais(2x-y\labais)(4x^2+2xy+y^2)\]

Uzdevumu piemērs kvadrātu starpības un kubu summas un starpības formulu izmantošanai

4. piemērs

Pavairot.

a) $((a+5))^2-9$

c) $-x^3+\frac(1)(27)$

Risinājums:

a) $((a+5))^2-9$

\[(((a+5))^2-9=(a+5))^2-3^2\]

Izmantojot kvadrātu starpības formulu, mēs iegūstam:

\[((a+5))^2-3^2=\left(a+5-3\right)\left(a+5+3\right)=\left(a+2\right)(a +8)\]

Rakstīsim šo izteiksmi šādā formā:

Pielietosim kubu kubu formulu:

c) $-x^3+\frac(1)(27)$

Rakstīsim šo izteiksmi šādā formā:

\[-x^3+\frac(1)(27)=(\left(\frac(1)(3)\right))^3-x^3\]

Pielietosim kubu kubu formulu:

\[(\left(\frac(1)(3)\right))^3-x^3=\left(\frac(1)(3)-x\right)\left(\frac(1)( 9)+\frac(x)(3)+x^2\right)\]

Samazinātas reizināšanas formulas vai kārtulas tiek izmantotas aritmētikā un, konkrētāk, algebrā, lai paātrinātu lielu algebrisko izteiksmju aprēķināšanas procesu. Pašas formulas ir atvasinātas no esošajiem noteikumiem algebrā vairāku polinomu reizināšanai.

Šo formulu izmantošana nodrošina diezgan ātru dažādu matemātisku problēmu risinājumu, kā arī palīdz vienkāršot izteiksmes. Algebrisko pārveidojumu noteikumi ļauj veikt dažas manipulācijas ar izteiksmēm, pēc kurām jūs varat iegūt izteiksmi vienādības kreisajā pusē, kas atrodas labajā pusē, vai pārveidot vienādības labo pusi (lai iegūtu izteiksmi kreisajā pusē aiz vienādības zīmes).

Ir ērti zināt formulas, ko izmanto saīsinātai reizināšanai ar atmiņu, jo tās bieži izmanto uzdevumu un vienādojumu risināšanā. Galvenās šajā sarakstā iekļautās formulas un to nosaukumi ir norādīti zemāk.

summas kvadrāts

Lai aprēķinātu summas kvadrātu, jāatrod summa, kas sastāv no pirmā vārda kvadrāta, pirmā un otrā reizinājuma divkāršās reizinājuma un otrā locekļa kvadrāta. Izteiksmes veidā šis noteikums tiek uzrakstīts šādi: (a + c)² = a² + 2ac + c².

Atšķirības kvadrāts

Lai aprēķinātu starpības kvadrātu, jāaprēķina summa, kas sastāv no pirmā skaitļa kvadrāta, pirmā skaitļa divreiz reizinājuma ar otro (ņemts ar pretējo zīmi) un otrā skaitļa kvadrāta. Izteiksmes veidā šis noteikums izskatās šādi: (a - c)² \u003d a² - 2ac + c².

Kvadrātu atšķirība

Formula divu skaitļu starpības kvadrātā ir vienāda ar šo skaitļu un to starpības summas reizinājumu. Izteiksmes veidā šis noteikums izskatās šādi: a² - c² \u003d (a + c) (a - c).

summas kubs

Lai aprēķinātu divu terminu summas kubu, ir jāaprēķina summa, kas sastāv no pirmā vārda kuba, trīskāršot pirmā un otrā vārda kvadrāta reizinājumu, no pirmā vārda trīskāršās reizinājuma un otrais kvadrāts, un otrā termiņa kubs. Izteiksmes veidā šis noteikums izskatās šādi: (a + c)³ \u003d a³ + 3a²c + 3ac² + c³.

Kubu summa

Saskaņā ar formulu tas ir vienāds ar šo terminu summas un to starpības nepilnīgā kvadrāta reizinājumu. Izteiksmes veidā šis noteikums izskatās šādi: a³ + c³ \u003d (a + c) (a² - ac + c²).

Piemērs. Ir jāaprēķina figūras tilpums, kas veidojas, pievienojot divus kubus. Ir zināmi tikai to sānu lielumi.

Ja sānu vērtības ir mazas, tad ir viegli veikt aprēķinus.

Ja malu garumi ir izteikti apgrūtinošos skaitļos, tad šajā gadījumā ir vieglāk piemērot formulu "Kubu summa", kas ievērojami vienkāršos aprēķinus.

atšķirības kubs

Kubiskās starpības izteiksme izklausās šādi: kā pirmā vārda trešās pakāpes summu trīskāršojiet pirmā vārda kvadrāta negatīvo reizinājumu ar otro, trīskāršojiet pirmā vārda reizinājumu ar otrā vārda kvadrātu. , un otrā termina negatīvais kubs. Matemātiskas izteiksmes veidā atšķirības kubs izskatās šādi: (a - c)³ \u003d a³ - 3a²c + 3ac² - c³.

Kubu atšķirība

Kubu starpības formula no kubu summas atšķiras tikai ar vienu zīmi. Tādējādi kubu starpība ir formula, kas vienāda ar šo skaitļu starpības reizinājumu ar to nepilno summas kvadrātu. Formā kubu atšķirība izskatās šādi: a 3 - c 3 \u003d (a - c) (a 2 + ac + c 2).

Piemērs. Ir jāaprēķina figūras tilpums, kas paliks pēc atņemšanas no zilā kuba tilpuma tilpuma skaitlis dzeltens, kas arī ir kubs. Ir zināms tikai maza un liela kuba malas izmērs.

Ja sānu vērtības ir mazas, tad aprēķini ir diezgan vienkārši. Un, ja malu garumi ir izteikti nozīmīgos skaitļos, tad ir vērts izmantot formulu ar nosaukumu "Kubu atšķirība" (vai "Atšķirības kubs"), kas ievērojami vienkāršos aprēķinus.