Vienādojums kopējos diferenciālos. Vienādojums kopējos diferenciāļos Pārbaudiet, vai dotā izteiksme ir kopējā diferenciāle

Problēmas izklāsts divdimensiju gadījumā

Vairāku mainīgo funkcijas rekonstrukcija no tās kopējās atšķirības

9.1. Problēmas izklāsts divdimensiju gadījumā. 72

9.2. Risinājuma apraksts. 72

Šis ir viens no otrā veida līklīnijas integrāļa lietojumiem.

Divu mainīgo funkcijas kopējās diferenciāļa izteiksme ir dota:

Atrodiet funkciju.

1. Tā kā ne katra formas izteiksme ir kādas funkcijas pilnīgs diferenciālis U(x,y), tad ir jāpārbauda uzdevuma formulējuma pareizība, tas ir, jāpārbauda nepieciešamais un pietiekams nosacījums kopējai diferenciālai, kas 2 mainīgo funkcijai ir formā . Šis nosacījums izriet no apgalvojumu (2) un (3) līdzvērtības iepriekšējās sadaļas teorēmā. Ja norādītais nosacījums ir izpildīts, tad problēmai ir risinājums, tas ir, funkcija U(x,y) var atjaunot; ja nosacījums nav izpildīts, problēmai nav risinājuma, tas ir, funkciju nevar atjaunot.

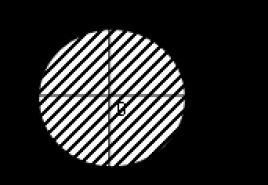
2. Funkciju var atrast no tās kopējā diferenciāļa, piemēram, izmantojot otrā veida līklīniju integrāli, aprēķinot to no līnijas, kas savieno fiksētu punktu ( x 0 ,y 0) un mainīgais punkts ( x;y) (Rīsi. 18):

Tādējādi tiek iegūts, ka kopējās diferenciāles otrā veida līknes integrālis dU(x,y) ir vienāds ar starpību starp funkcijas vērtībām U(x,y) integrācijas līnijas beigu un sākuma punktos.

Zinot šo rezultātu tagad, mums ir jāaizstāj dU izliektajā integrāļa izteiksmē un aprēķiniet integrāli pa lauzto līniju ( ACB), ņemot vērā tā neatkarību no integrācijas līnijas formas:

ieslēgts ( A.C.): ieslēgts ( ZA) :

(1)

Tādējādi ir iegūta formula, ar kuras palīdzību no tās kopējās diferenciāles tiek atjaunota 2 mainīgo funkcija.

3. Ir iespējams atjaunot funkciju no tās kopējās diferenciālās tikai līdz konstantam termiņam, jo d(U+ const) = dU. Tāpēc uzdevuma risināšanas rezultātā iegūstam funkciju kopumu, kas viena no otras atšķiras ar nemainīgu termiņu.

Piemēri (divu mainīgo funkcijas rekonstrukcija no tās kopējās atšķirības)

1. Atrast U(x,y), Ja dU = (x 2 – y 2)dx – 2xydy.

Mēs pārbaudām divu mainīgo funkcijas kopējās atšķirības nosacījumu:

Pilnīgs diferenciāļa nosacījums ir izpildīts, kas nozīmē funkciju U(x,y) var atjaunot.

Pārbaudiet: – taisnība.

Atbilde: U(x,y) = x 3 /3 – xy 2 + C.

2. Atrodiet tādu funkciju, ka

Mēs pārbaudām nepieciešamos un pietiekamos nosacījumus trīs mainīgo funkcijas pilnīgai diferenciālai: , , , ja ir dota izteiksme.

Atrisināmajā problēmā

visi nosacījumi pilnīgam diferenciālam ir izpildīti, tāpēc funkciju var atjaunot (problēma ir pareizi formulēta).

Mēs atjaunosim funkciju, izmantojot otrā veida līklīniju integrāli, aprēķinot to pa noteiktu līniju, kas savieno fiksēto punktu un mainīgo punktu, jo

(šī vienādība tiek iegūta tāpat kā divdimensiju gadījumā).

No otras puses, otrā veida līknes integrālis no kopējās diferenciāles nav atkarīgs no integrācijas taisnes formas, tāpēc to visvieglāk ir aprēķināt pa lauztu līniju, kas sastāv no koordinātu asīm paralēliem segmentiem. Šajā gadījumā kā fiksētu punktu var vienkārši ņemt punktu ar konkrētām skaitliskām koordinātām, uzraugot tikai to, lai šajā punktā un visā integrācijas līnijā tiktu izpildīts līklīnijas integrāļa pastāvēšanas nosacījums (tas ir, lai funkcijas un ir nepārtrauktas). Ņemot vērā šo piezīmi, šajā uzdevumā kā fiksētu punktu varam ņemt, piemēram, punktu M 0. Tad mums būs uz katras lauztās līnijas saites

10.2. Pirmā veida virsmas integrāļa aprēķins. 79

10.3. Daži pirmā veida virsmas integrāļa pielietojumi. 81

Var gadīties, ka diferenciālvienādojuma kreisā puse

ir kādas funkcijas kopējā atšķirība:

un tāpēc vienādojums (7) iegūst formu .

Ja funkcija ir (7) vienādojuma risinājums, tad , un tāpēc

kur ir konstante un otrādi, ja kāda funkcija galīgo vienādojumu (8) pārvērš par identitāti, tad, diferencējot iegūto identitāti, iegūstam , un tāpēc , kur ir patvaļīga konstante, ir oriģināla vispārējais integrālis vienādojums.

Ja ir norādītas sākotnējās vērtības, tad konstante tiek noteikta no (8) un

ir vēlamais daļējais integrālis. Ja punktā , tad vienādojums (9) ir definēts kā netieša funkcija .

Lai vienādojuma (7) kreisā puse būtu kādas funkcijas pilnīgs diferenciālis, ir nepieciešams un pietiekami, ka

Ja šis Eilera noteiktais nosacījums ir izpildīts, tad vienādojumu (7) var viegli integrēt. Tiešām, . Citā pusē, . Tāpēc

Aprēķinot integrāli, lielums tiek uzskatīts par konstanti, tāpēc tā ir patvaļīga funkcija. Lai noteiktu funkciju, mēs diferencējam atrasto funkciju attiecībā pret un, tā kā , iegūstam

No šī vienādojuma mēs nosakām un, integrējot, atrodam .

Kā jūs zināt no kursa matemātiskā analīze, pat vienkāršāk, jūs varat definēt funkciju pēc tās kopējās diferenciāļa, ņemot līknes integrāli starp noteiktu punktu un punktu ar mainīgām koordinātām jebkurā ceļā:

Visbiežāk kā integrācijas ceļu ir ērti ņemt lauztu līniju, kas sastāv no divām saitēm paralēli koordinātu asīm; šajā gadījumā

Piemērs. .

Vienādojuma kreisā puse ir kādas funkcijas kopējā diferenciāle, jo

Tāpēc vispārējam integrālim ir forma

Funkcijas definēšanai var izmantot citu metodi:

Mēs izvēlamies, piemēram, koordinātu sākumpunktu kā sākumpunktu un lauztu līniju kā integrācijas ceļu. Tad

un vispārējam integrālim ir forma

Kas sakrīt ar iepriekšējo rezultātu, kas noved pie kopsaucēja.

Dažos gadījumos, kad (7) vienādojuma kreisā puse nav pilnīgs diferenciālis, ir viegli izvēlēties funkciju, pēc kuras reizināšanas (7) vienādojuma kreisā puse pārvēršas par pilnīgu diferenciāli. Šo funkciju sauc integrējošais faktors. Ņemiet vērā, ka reizināšana ar integrējošo koeficientu var novest pie nevajadzīgu daļēju risinājumu parādīšanās, kas šo koeficientu pārvērš līdz nullei.

Piemērs. .

Acīmredzot pēc reizināšanas ar koeficientu kreisā puse pārvēršas par kopējo diferenciāli. Patiešām, pēc reizināšanas ar mēs iegūstam

vai, integrējot, . Reizinot ar 2 un pastiprinot, mēs iegūstam .

Protams, ne vienmēr integrējošais faktors tiek izvēlēts tik vienkārši. Vispārīgā gadījumā, lai atrastu integrējošo faktoru, ir jāizvēlas vismaz viens vienādojuma daļējs atrisinājums parciālos atvasinājumos vai izvērstā veidā, kas nav identiski nulle

kas pēc dalīšanas ar un dažu terminu pārcelšanas uz citu vienādības daļu tiek reducēta līdz formai

Vispārīgā gadījumā šī daļējā diferenciālvienādojuma integrēšana nekādā ziņā nav vienkāršāks uzdevums kā sākotnējā vienādojuma integrēšana, taču dažos gadījumos konkrēta (11) vienādojuma risinājuma izvēle nav grūta.

Turklāt, ņemot vērā, ka integrējošais faktors ir tikai viena argumenta funkcija (piemēram, tā ir funkcija tikai vai tikai , vai funkcija tikai , vai tikai utt.), var viegli integrēt vienādojumu (11) un norāda nosacījumus, kādos pastāv aplūkojamā tipa integrējošais faktors. Tas identificē vienādojumu klases, kurām var viegli atrast integrējošo faktoru.

Piemēram, atradīsim nosacījumus, kādos vienādojumam ir integrējošais faktors, kas ir atkarīgs tikai no , t.i. . Šajā gadījumā vienādojums (11) ir vienkāršots un iegūst formu , no kurienes, ņemot vērā nepārtraukta funkcija no , mēs saņemam

Ja ir funkcija tikai no , tad integrējošais faktors, kas ir atkarīgs tikai no , pastāv un ir vienāds ar (12), pretējā gadījumā formas integrējošais faktors nepastāv.

Nosacījums par integrējošā faktora pastāvēšanu atkarībā tikai no tiek izpildīts, piemēram, par lineārais vienādojums vai . Patiešām, un tāpēc . Pilnīgi līdzīgi var atrast nosacījumus formas integrējošo faktoru pastāvēšanai utt.

Piemērs. Vai vienādojumam ir formas integrējošais faktors?

Apzīmēsim . Vienādojums (11) pie ieņem formu , no kurienes vai

Lai pastāvētu noteikta veida integrējošais faktors, ir nepieciešams un, pieņemot nepārtrauktības pieņēmumu, pietiekami, lai tas būtu tikai funkcija. Tāpēc šajā gadījumā integrējošais faktors pastāv un ir vienāds ar (13). Kad saņemam. Reizinot sākotnējo vienādojumu ar , mēs to reducējam līdz formai

Integrējot, mēs iegūstam , un pēc potenciācijas mums būs vai polārajās koordinātēs - logaritmisko spirāļu saime.

Piemērs. Atrodiet spoguļa formu, kas paralēli noteiktam virzienam atspoguļo visus starus, kas izplūst no noteiktā punkta.

Novietosim koordinātu sākumpunktu dotajā punktā un virzīsim abscisu asi paralēli uzdevuma nosacījumos norādītajam virzienam. Ļaujiet staram krist uz spoguļa punktā . Apskatīsim spoguļa daļu plaknē, kas iet caur abscisu asi un punktu . Nozīmēsim pieskare aplūkojamās spoguļa virsmas griezumam punktā . Kopš staru kūļa krišanas leņķa vienāds ar leņķi atspulgs, tad trīsstūris ir vienādsānu. Tāpēc

Iegūtais viendabīgais vienādojums ir viegli integrējams, mainot mainīgos, bet vēl vienkāršāk, atbrīvojoties no saucējā iracionalitātes, to pārrakstīt formā . Šim vienādojumam ir acīmredzams integrējošais faktors , , , (parabolu saime).

Šo uzdevumu var atrisināt vēl vienkāršāk koordinātēs un , kur , un vajadzīgo virsmu griezuma vienādojums iegūst formu .

Ir iespējams pierādīt integrējoša faktora esamību vai, kas ir tas pats, nulles atrisinājuma esamību daļējam diferenciālvienādojumam (11) kādā jomā, ja funkcijām un ir nepārtraukti atvasinājumi un vismaz viens no šiem. funkcijas nepazūd. Tāpēc integrējošā faktora metodi var uzskatīt par vispārīga metode integrējot vienādojumus formas , tomēr integrējošā faktora atrašanas grūtības dēļ šo metodi visbiežāk izmanto gadījumos, kad integrējošais faktors ir acīmredzams.

Parādīts, kā atpazīt diferenciālvienādojums pilnos diferenciālos. Ir dotas metodes tās risināšanai. Ir dots piemērs vienādojuma risināšanai kopējos diferenciāļos divos veidos.

Saturs

Ievads

Pirmās kārtas diferenciālvienādojums kopējos diferenciāļos ir vienādojums ar šādu formu:
(1) ,
kur vienādojuma kreisā puse ir kādas funkcijas U kopējā diferenciāle (x, y) no mainīgajiem x, y:
.
Kurā .

Ja tiek atrasta šāda funkcija U (x, y), tad vienādojums iegūst šādu formu:
dU (x, y) = 0.
Tās vispārējais integrālis ir:
U (x, y) = C,
kur C ir konstante.

Ja pirmās kārtas diferenciālvienādojums ir uzrakstīts tā atvasinājuma izteiksmē:
,
tad to ir viegli ieviest formā (1) . Lai to izdarītu, reiziniet vienādojumu ar dx. Tad .
(1) .

Rezultātā mēs iegūstam vienādojumu, kas izteikts ar diferenciāļiem:

Diferenciālvienādojuma īpašība kopējos diferenciāļos (1) Lai vienādojums
(2) .

bija vienādojums kopējos diferenciālos, tas ir nepieciešams un pietiekams, lai attiecība pastāvētu:

Pierādījums Turklāt mēs pieņemam, ka visas pierādījumā izmantotās funkcijas ir definētas un tām ir atbilstoši atvasinājumi dažos mainīgo x un y vērtību diapazonos. Punkts x 0, g 0

arī pieder šai zonai..
Pierādīsim nosacījuma (2) nepieciešamību (1) Ļaujiet vienādojuma kreisajai pusei (x, y):
.
ir kādas funkcijas U diferenciālis
;
.
Tad
;
.
Tā kā otrais atvasinājums nav atkarīgs no diferenciācijas kārtības, tad (2) No tā izriet, ka .

Nepieciešamības nosacījums.
pierādīts. (2) :
(2) .
Pierādīsim nosacījuma (2) pietiekamību (x, y) Lai nosacījums ir izpildīts
.
Parādīsim, ka ir iespējams atrast šādu funkciju U (x, y) ka tā atšķirība ir:
(3) ;
(4) .
Tas nozīmē, ka pastāv šāda funkcija U (3) , kas apmierina vienādojumus: 0 Atradīsim šādu funkciju. Integrēsim vienādojumu
;
;
(5) .
ar x no x (2) :

.
uz x, pieņemot, ka y ir konstante: (4) Mēs atšķiram attiecībā pret y, pieņemot, ka x ir konstante un tiek piemērota
.
Vienādojums 0 tiks izpildīts, ja
;
;
.
Integrēt virs y no y (5) :
(6) .
rotaļlieta:
.
Aizstāt iekšā

Tātad, mēs esam atraduši funkciju, kuras diferenciālis (6) Pietiekamība ir pierādīta. Formulā,U (x, y)(x 0, y 0) Turklāt mēs pieņemam, ka visas pierādījumā izmantotās funkcijas ir definētas un tām ir atbilstoši atvasinājumi dažos mainīgo x un y vērtību diapazonos. Punkts x ir konstante - funkcijas U vērtība

punktā x

. Tam var piešķirt jebkuru vērtību.
(1) .
Kā atpazīt diferenciālvienādojumu kopējos diferenciāļos (2) :
(2) .
Ja tas ir spēkā, tad šis vienādojums ir kopējos diferenciālos. Ja nē, tad tas nav kopējais diferenciālvienādojums.

Piemērs

Pārbaudiet, vai vienādojums ir kopējos diferenciālos:
.

Šeit
, .
Mēs atšķiram attiecībā pret y, ņemot vērā x konstanti:


.
Atšķirsim


.
Tāpēc ka:
,
tad dotais vienādojums ir summāros diferenciālos.

Kopējo diferenciāļu diferenciālvienādojumu risināšanas metodes

Secīgās diferenciālās ekstrakcijas metode

Lielākā daļa vienkārša metode vienādojuma atrisināšana kopējos diferenciāļos ir diferenciāļa secīgas atlases metode. Lai to izdarītu, mēs izmantojam diferenciācijas formulas, kas rakstītas diferenciālā formā:
du ± dv = d (u ± v);
v du + u dv = d (uv);
;
.
Šajās formulās u un v ir patvaļīgas izteiksmes, ko veido jebkura mainīgo kombinācija.

1. piemērs

Atrisiniet vienādojumu:
.

Iepriekš mēs noskaidrojām, ka šis vienādojums ir kopējos diferenciālos. Pārveidosim to:
(P1) .
Mēs atrisinām vienādojumu, secīgi izolējot diferenciāli.
;
;
;
;

.
Integrēt virs y no y (P1):
;
.

Secīgās integrācijas metode

Šajā metodē mēs meklējam funkciju U (x, y), kas apmierina vienādojumus:
(3) ;
(4) .

Integrēsim vienādojumu (3) x, ņemot vērā y konstantu:
.
Šeit φ (y)- patvaļīga y funkcija, kas ir jānosaka. Tā ir integrācijas konstante. Aizstāt vienādojumā (4) :
.
No šejienes:
.
Integrējot, mēs atrodam φ (y) un tādējādi U (x, y).

2. piemērs

Atrisiniet vienādojumu kopējos diferenciālos:
.

Iepriekš mēs noskaidrojām, ka šis vienādojums ir kopējos diferenciālos. Ieviesīsim šādu apzīmējumu:
, .
Meklēju funkciju U (x, y), kuras diferenciālis ir vienādojuma kreisā puse:
.
Pēc tam:
(3) ;
(4) .
Integrēsim vienādojumu (3) x, ņemot vērā y konstantu:
(P2)
.
Atšķirt attiecībā uz y:

.
Aizstāsim (4) :
;
.
Integrēsim:
.
Aizstāsim (P2):

.
Vienādojuma vispārējais integrālis:
U (x, y) = konst.
Mēs apvienojam divas konstantes vienā.

Integrācijas pa līkni metode

Funkcija U, ko nosaka attiecība:
dU = p (x, y) dx + q(x, y) dy,
var atrast, integrējot šo vienādojumu pa līkni, kas savieno punktus Formulā Un (x, y):
(7) .
Tāpēc ka
(8) ,
tad integrālis ir atkarīgs tikai no sākuma koordinātām Formulā un galīgs (x, y) punktu un nav atkarīgs no līknes formas. No (7) Un (8) mēs atradām:
(9) .
Šeit x 0 un y 0 - pastāvīgs. Tāpēc U Formulā- arī nemainīgs.

Šādas U definīcijas piemērs tika iegūts pierādījumā:
(6) .
Šeit integrācija tiek veikta vispirms segmentā, paralēli asij y, no punkta (x 0 , y 0 ) līdz punktam (x 0, y). Pēc tam tiek veikta integrācija pa segmentu, kas ir paralēls x asij no punkta (x 0, y) līdz punktam (x, y) .

Vispārīgāk, jums ir jāattēlo līknes vienādojums, kas savieno punktus (x 0 , y 0 ) Un (x, y) parametru formā:
x 1 = s(t 1); y 1 = r(t 1);
x 0 = s(t 0); y 0 = r(t 0);
x = s (t); y = r (t);
un integrēt pa t 1 no t 0 uz t.

Vienkāršākais veids, kā veikt integrāciju, ir segmenta savienojuma punkti (x 0 , y 0 ) Un (x, y). Šajā gadījumā:
x 1 = x 0 + (x - x 0) t 1; y 1 = y 0 + (y - y 0) t 1;
t 0 = 0 ; t = 1 ;
dx 1 = (x - x 0) dt 1; dy 1 = (y - y 0) dt 1.
Pēc aizstāšanas mēs iegūstam integrāli virs t of 0 pirms tam 1 .
Šī metode tomēr rada diezgan apgrūtinošus aprēķinus.

Atsauces:
V.V. Stepanovs, Diferenciālvienādojumu kurss, "LKI", 2015.

Diferenciāls sauc par formas vienādojumu

P(x,y)dx + J(x,y)dy = 0 ,

kur kreisā puse ir divu mainīgo jebkuras funkcijas kopējā diferenciāle.

Apzīmēsim divu mainīgo nezināmo funkciju (tas ir jāatrod, risinot vienādojumus kopējos diferenciāļos) F un mēs pie tā drīz atgriezīsimies.

Pirmā lieta, kas jums jāpievērš uzmanība, ir tāda, ka vienādojuma labajā pusē ir jābūt nullei, un zīmei, kas savieno divus vārdus kreisajā pusē, jābūt plusam.

Otrkārt, ir jāievēro zināma vienlīdzība, kas apstiprina, ka šis diferenciālvienādojums ir vienādojums kopējos diferenciālos. Šī pārbaude ir obligāta algoritma sastāvdaļa vienādojumu risināšanai kopējos diferenciāļos (tas ir šīs nodarbības otrajā rindkopā), tāpēc funkcijas atrašanas process F diezgan darbietilpīgs, un ir svarīgi sākotnējā posmā pārliecināties, ka mēs netērējam laiku.

Tātad nezināmā funkcija, kas jāatrod, tiek apzīmēta ar F. Visu neatkarīgo mainīgo daļējo diferenciāļu summa dod kopējo diferenciāli. Tāpēc, ja vienādojums ir kopējais diferenciālvienādojums, vienādojuma kreisā puse ir daļējo diferenciāļu summa. Tad pēc definīcijas

dF = P(x,y)dx + J(x,y)dy .

Atcerēsimies formulu divu mainīgo funkcijas kopējās diferenciālas aprēķināšanai:

Atrisinot pēdējās divas vienādības, varam rakstīt

.

Mēs atšķiram pirmo vienādību attiecībā uz mainīgo “y”, otro - attiecībā uz mainīgo “x”:

.

kas ir nosacījums, lai dotais diferenciālvienādojums patiešām būtu pilnīgs diferenciālvienādojums.

Algoritms diferenciālvienādojumu risināšanai kopējos diferenciāļos

1. darbība. Pārliecinieties, vai vienādojums ir kopējais diferenciālvienādojums. Lai izteiksme bija kādas funkcijas kopējā atšķirība F(x, y) ir nepieciešams un pietiekams, lai . Citiem vārdiem sakot, jums ir jāņem daļējs atvasinājums attiecībā uz x un daļējais atvasinājums attiecībā uz y cits termins un, ja šie atvasinājumi ir vienādi, tad vienādojums ir kopējais diferenciālvienādojums.

2. darbība. Pierakstiet daļēju diferenciālvienādojumu sistēmu, kas veido funkciju F:

3. darbība. Integrējiet sistēmas pirmo vienādojumu - ar x (y F:

,
y.

Alternatīva iespēja (ja šādā veidā ir vieglāk atrast integrāli) ir integrēt sistēmas otro vienādojumu - ar y (x paliek konstante un tiek izņemta no integrāļa zīmes). Tādā veidā tiek atjaunota arī funkcija F:

,
kur ir vēl nezināma funkcija X.

4. darbība. 3. darbības rezultāts (atrasts vispārējais integrālis) tiek diferencēts ar y(alternatīvi - saskaņā ar x) un pielīdzina sistēmas otrajam vienādojumam:

,

un alternatīvā versijā - uz pirmo sistēmas vienādojumu:

.

No iegūtā vienādojuma mēs nosakām (alternatīvi)

5. darbība. 4. darbības rezultāts ir integrācija un atrašana (vai arī atrast).

6. darbība. Aizstāt 5. darbības rezultātu ar 3. darbības rezultātu — ar daļējas integrācijas atjaunoto funkciju F. Patvaļīga konstante C bieži rakstīts aiz vienādības zīmes - vienādojuma labajā pusē. Tā mēs iegūstam kopīgs lēmums diferenciālvienādojums kopējos diferenciāļos. Tam, kā jau minēts, ir forma F(x, y) = C.

Diferenciālvienādojumu atrisinājumu piemēri kopējos diferenciāļos

1. piemērs.

1. darbība. vienādojums kopējos diferenciāļos x viens termins izteiksmes kreisajā pusē

un daļējais atvasinājums attiecībā uz y cits termins
vienādojums kopējos diferenciāļos .

2. darbība. F:

3. darbība. Autors x (y paliek konstante un tiek izņemta no integrāļa zīmes). Tādējādi mēs atjaunojam funkciju F:

kur ir vēl nezināma funkcija y.

4. darbība. y

.

.

5. darbība.

6. darbība. F. Patvaļīga konstante C :
.

Kāda kļūda šeit, visticamāk, var rasties? Visizplatītākās kļūdas ir ņemt daļēju integrāli pār vienu no mainīgajiem funkciju reizinājuma parastajam integrālam un mēģināt integrēt pa daļām vai aizvietošanas mainīgo, kā arī ņemt divu faktoru daļējo atvasinājumu kā atvasinājumu funkciju reizinājumu un meklējiet atvasinājumu, izmantojot atbilstošo formulu.

Tas ir jāatceras: aprēķinot daļēju integrāli attiecībā pret vienu no mainīgajiem, otrs ir konstante un tiek izņemts no integrāļa zīmes, un, aprēķinot daļējo atvasinājumu attiecībā pret vienu no mainīgajiem, otrs ir arī konstante, un izteiksmes atvasinājums tiek atrasts kā “darbojošā” mainīgā atvasinājums, kas reizināts ar konstanti.

Starp vienādojumi kopējos diferenciāļos Nereti var atrast piemērus ar eksponenciālu funkciju. Šis ir nākamais piemērs. Tas ir ievērojams arī ar to, ka tā risinājumā tiek izmantota alternatīva iespēja.

2. piemērs. Atrisiniet diferenciālvienādojumu

.

1. darbība. Pārliecināsimies, ka vienādojums ir vienādojums kopējos diferenciāļos . Lai to izdarītu, mēs atrodam daļēju atvasinājumu attiecībā uz x viens termins izteiksmes kreisajā pusē

un daļējais atvasinājums attiecībā uz y cits termins
. Šie atvasinājumi ir vienādi, kas nozīmē, ka vienādojums ir vienādojums kopējos diferenciāļos .

2. darbība. Uzrakstīsim daļēju diferenciālvienādojumu sistēmu, kas veido funkciju F:

3. darbība. Integrēsim otro sistēmas vienādojumu - by y (x paliek konstante un tiek izņemta no integrāļa zīmes). Tādējādi mēs atjaunojam funkciju F:

kur ir vēl nezināma funkcija X.

4. darbība. Mēs atšķiram 3. darbības rezultātu (atrasts vispārējais integrālis) attiecībā uz X

un pielīdzina sistēmas pirmajam vienādojumam:

No iegūtā vienādojuma mēs nosakām:
.

5. darbība. Mēs integrējam 4. darbības rezultātu un atrodam:
.

6. darbība. Mēs aizstājam 5. darbības rezultātu ar 3. darbības rezultātu - funkciju, kas atjaunota ar daļēju integrāciju F. Patvaļīga konstante C rakstiet aiz vienādības zīmes. Tādējādi mēs iegūstam kopējo summu diferenciālvienādojuma atrisināšana kopējos diferenciāļos :
.

Nākamajā piemērā mēs atgriežamies no alternatīvas opcijas pie galvenās.

3. piemērs. Atrisiniet diferenciālvienādojumu

1. darbība. Pārliecināsimies, ka vienādojums ir vienādojums kopējos diferenciāļos . Lai to izdarītu, mēs atrodam daļēju atvasinājumu attiecībā uz y viens termins izteiksmes kreisajā pusē

un daļējais atvasinājums attiecībā uz x cits termins
. Šie atvasinājumi ir vienādi, kas nozīmē, ka vienādojums ir vienādojums kopējos diferenciāļos .

2. darbība. Uzrakstīsim daļēju diferenciālvienādojumu sistēmu, kas veido funkciju F:

3. darbība. Integrēsim pirmo sistēmas vienādojumu - Autors x (y paliek konstante un tiek izņemta no integrāļa zīmes). Tādējādi mēs atjaunojam funkciju F:

kur ir vēl nezināma funkcija y.

4. darbība. Mēs atšķiram 3. darbības rezultātu (atrasts vispārējais integrālis) attiecībā uz y

un pielīdzina sistēmas otrajam vienādojumam:

No iegūtā vienādojuma mēs nosakām:
.

5. darbība. Mēs integrējam 4. darbības rezultātu un atrodam:

6. darbība. Mēs aizstājam 5. darbības rezultātu ar 3. darbības rezultātu - funkciju, kas atjaunota ar daļēju integrāciju F. Patvaļīga konstante C rakstiet aiz vienādības zīmes. Tādējādi mēs iegūstam kopējo summu diferenciālvienādojuma atrisināšana kopējos diferenciāļos :
.

4. piemērs. Atrisiniet diferenciālvienādojumu

1. darbība. Pārliecināsimies, ka vienādojums ir vienādojums kopējos diferenciāļos . Lai to izdarītu, mēs atrodam daļēju atvasinājumu attiecībā uz y viens termins izteiksmes kreisajā pusē

un daļējais atvasinājums attiecībā uz x cits termins
. Šie atvasinājumi ir vienādi, kas nozīmē, ka vienādojums ir kopējais diferenciālvienādojums.

2. darbība. Uzrakstīsim daļēju diferenciālvienādojumu sistēmu, kas veido funkciju F:

3. darbība. Integrēsim pirmo sistēmas vienādojumu - Autors x (y paliek konstante un tiek izņemta no integrāļa zīmes). Tādējādi mēs atjaunojam funkciju F:

kur ir vēl nezināma funkcija y.

4. darbība. Mēs atšķiram 3. darbības rezultātu (atrasts vispārējais integrālis) attiecībā uz y

un pielīdzina sistēmas otrajam vienādojumam:

No iegūtā vienādojuma mēs nosakām:
.

5. darbība. Mēs integrējam 4. darbības rezultātu un atrodam:

6. darbība. Mēs aizstājam 5. darbības rezultātu ar 3. darbības rezultātu - funkciju, kas atjaunota ar daļēju integrāciju F. Patvaļīga konstante C rakstiet aiz vienādības zīmes. Tādējādi mēs iegūstam kopējo summu diferenciālvienādojuma atrisināšana kopējos diferenciāļos :
.

5. piemērs. Atrisiniet diferenciālvienādojumu

.

1. darbība. Pārliecināsimies, ka vienādojums ir vienādojums kopējos diferenciāļos . Lai to izdarītu, mēs atrodam daļēju atvasinājumu attiecībā uz y viens termins izteiksmes kreisajā pusē

un daļējais atvasinājums attiecībā uz x cits termins
. Šie atvasinājumi ir vienādi, kas nozīmē, ka vienādojums ir vienādojums kopējos diferenciāļos .

Šajā tēmā mēs aplūkosim funkcijas atjaunošanas metodi no tās kopējā diferenciāļa, sniegsim piemērus problēmām ar pilnīga analīze risinājumus.

Gadās, ka diferenciālvienādojumi (DE) formā P (x, y) d x + Q (x, y) d y = 0 kreisajā pusē var saturēt pilnīgus dažu funkciju diferenciāļus. Tad mēs varam atrast diferenciālvienādojuma vispārējo integrāli, ja vispirms rekonstruējam funkciju no tās kopējā diferenciāļa.

1. piemērs

Apsveriet vienādojumu P (x, y) d x + Q (x, y) d y = 0. Kreisajā pusē ir noteiktas funkcijas diferenciālis U(x, y) = 0. Lai to izdarītu, ir jāizpilda nosacījums ∂ P ∂ y ≡ ∂ Q ∂ x.

Funkcijas U (x, y) = 0 kopējā diferenciāļa forma ir d U = ∂ U ∂ x d x + ∂ U ∂ y d y. Ņemot vērā nosacījumu ∂ P ∂ y ≡ ∂ Q ∂ x mēs iegūstam:

P (x , y) d x + Q (x , y) d y = ∂ U ∂ x d x + ∂ U ∂ y d y

∂ U ∂ x = P (x, y) ∂ U ∂ y = Q (x, y)

Pārveidojot pirmo vienādojumu no iegūtās vienādojumu sistēmas, mēs varam iegūt:

U (x, y) = ∫ P (x, y) d x + φ (y)

Funkciju φ (y) varam atrast no iepriekš iegūtās sistēmas otrā vienādojuma:
∂ U (x, y) ∂ y = ∂ ∫ P (x, y) d x ∂ y + φ y " (y) = Q (x, y) ⇒ φ (y) = ∫ Q (x, y) - ∂ ∫ P (x , y) d x ∂ y d y

Tādā veidā mēs atradām vēlamo funkciju U (x, y) = 0.

2. piemērs

Atrodiet vispārīgo risinājumu diferenciālvienādojumam (x 2 - y 2) d x - 2 x y d y = 0.

Risinājums

P (x, y) = x 2 - y 2, Q (x, y) = - 2 x y

Pārbaudīsim, vai nosacījums ∂ P ∂ y ≡ ∂ Q ∂ x ir izpildīts:

∂ P ∂ y = ∂ (x 2 - y 2) ∂ y = - 2 y ∂ Q ∂ x = ∂ (- 2 x y) ∂ x = - 2 y

Mūsu nosacījums ir izpildīts.

Pamatojoties uz aprēķiniem, varam secināt, ka sākotnējā diferenciālvienādojuma kreisā puse ir kādas funkcijas U (x, y) = 0 kopējā diferenciāle. Mums ir jāatrod šī funkcija.

Tā kā (x 2 - y 2) d x - 2 x y d y ir funkcijas U (x, y) = 0 kopējā diferenciāle, tad

∂ U ∂ x = x 2 - y 2 ∂ U ∂ y = - 2 x y

Integrēsim sistēmas pirmo vienādojumu attiecībā pret x:

U (x, y) = ∫ (x 2 - y 2) d x + φ (y) = x 3 3 - x y 2 + φ (y)

Tagad mēs diferencējam iegūto rezultātu attiecībā uz y:

∂ U ∂ y = ∂ x 3 3 - x y 2 + φ (y) ∂ y = - 2 x y + φ y " (y)

Pārveidojot sistēmas otro vienādojumu, iegūstam: ∂ U ∂ y = - 2 x y . Tas nozīmē, ka
- 2 x y + φ y " (y) = - 2 x y φ y " (y) = 0 ⇒ φ (y) = ∫ 0 d x = C

kur C ir patvaļīga konstante.

Mēs iegūstam: U (x, y) = x 3 3 - x y 2 + φ (y) = x 3 3 - x y 2 + C. Sākotnējā vienādojuma vispārējais integrālis ir x 3 3 - x y 2 + C = 0.

Apskatīsim citu metodi funkcijas atrašanai, izmantojot zināmu kopējo diferenciāli. Tas ietver līklīnijas integrāļa izmantošanu no fiksēta punkta (x 0, y 0) līdz punktam ar mainīgām koordinātām (x, y):

U (x , y) = ∫ (x 0 , y 0) (x , y) P (x , y) d x + Q (x , y) d y + C

Šādos gadījumos integrāļa vērtība nekādā veidā nav atkarīga no integrācijas ceļa. Par integrācijas ceļu varam ņemt lauztu līniju, kuras saites atrodas paralēli koordinātu asīm.

3. piemērs

Atrodiet vispārīgo atrisinājumu diferenciālvienādojumam (y - y 2) d x + (x - 2 x y) d y = 0.

Risinājums

Pārbaudīsim, vai nosacījums ∂ P ∂ y ≡ ∂ Q ∂ x ir izpildīts:

∂ P ∂ y = ∂ (y - y 2) ∂ y = 1 - 2 y ∂ Q ∂ x = ∂ (x - 2 x y) ∂ x = 1 - 2 y

Izrādās, ka diferenciālvienādojuma kreiso pusi attēlo kādas funkcijas kopējā diferenciāle U (x, y) = 0. Lai atrastu šo funkciju, ir jāaprēķina punkta taisnes integrālis (1 ; 1) pirms tam (x, y). Ņemsim par integrācijas ceļu lauztu līniju, kuras posmi iet pa taisnu līniju y = 1 no punkta (1, 1) uz (x, 1) un pēc tam no punkta (x, 1) uz (x, y):

∫ (1 , 1) (x , y) y - y 2 d x + (x - 2 x y) d y = = ∫ (1 , 1) (x , 1) (y - y 2) d x + (x - 2 x y) ) d y + + ∫ (x , 1) (x , y) (y - y 2) d x + (x - 2 x y) d y = = ∫ 1 x (1 - 1 2) d x + ∫ 1 y (x - 2) x y) d y = (x y - x y 2) y 1 = = x y - x y 2 - (x 1 - x 1 2) = x y - x y 2

Mēs esam ieguvuši vispārīgu risinājumu diferenciālvienādojumam formā x y - x y 2 + C = 0.

4. piemērs

Nosakiet diferenciālvienādojuma y · cos x d x + sin 2 x d y = 0 vispārīgo risinājumu.

Risinājums

Pārbaudīsim, vai nosacījums ∂ P ∂ y ≡ ∂ Q ∂ x ir izpildīts.

Tā kā ∂ (y · cos x) ∂ y = cos x, ∂ (sin 2 x) ∂ x = 2 sin x · cos x, tad nosacījums netiks izpildīts. Tas nozīmē, ka diferenciālvienādojuma kreisā puse nav pilnīgs funkcijas diferenciālis. Šis ir diferenciālvienādojums ar atdalāmiem mainīgajiem, un tā risināšanai ir piemēroti citi risinājumi.

Ja pamanāt tekstā kļūdu, lūdzu, iezīmējiet to un nospiediet Ctrl+Enter