Prezentācija par tēmu: Atvasinājums. No atvasinājuma Atvasinājums ķīmijā radīšanas vēstures

Funkcijas atvasinājums GAPOU RO "RKTM" skolotāja Kolykhalina K.A. Argumenta inkrements, funkcijas palielinājums Lai x ir patvaļīgs punkts, kas atrodas kādā fiksēta punkta x0 tuvumā. Atšķirību x-x0 sauc par neatkarīgā mainīgā palielinājumu (vai argumenta pieaugumu) punktā x0 un apzīmē ar ∆x. ∆x = x – x0 – neatkarīgā mainīgā lieluma pieaugums. Funkcijas f pieaugums punktā x0 ir starpība starp funkcijas vērtībām patvaļīgā punktā un funkcijas vērtību fiksētā punktā. f(х) – f(х0)=f(х0+∆х) – f(х0) – funkcijas pieaugums f∆f=f(х0+∆х) – f(х0) Atvasinātās funkcijas y= atvasinājuma noteikšana f(x) punktā x =x0 sauc par funkcijas ∆y pieauguma attiecības robežu šajā punktā pret argumenta ∆x pieaugumu, jo argumenta pieaugumam ir tendence uz nulli. Atvasinājuma aprēķināšanas algoritms Funkcijas y= f(x) atvasinājumu var atrast pēc šādas shēmas: 1. Palielināsim ∆x≠0 līdz argumentam x un atrodam funkcijas y+∆y= f palielināto vērtību. (x+∆x). 2. Atrodiet funkcijas ∆y= f(x+∆x) - f(x) inkrementu. 3. Sastādiet relāciju 4. Atrodiet šīs attiecības robežu pie ∆x⇾0, t.i. (ja šis ierobežojums pastāv). Funkcijas atvasinājuma noteikšana dotajā punktā. Tās ģeometriskā nozīme

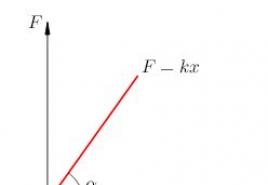
k - taisnas līnijas slīpums (sekants)

Pieskares

Atvasinājuma ģeometriskā nozīme

Funkcijas atvasinājums dotajā punktā ir vienāds ar pieskares slīpumu, kas novilkta funkcijas grafikam šajā punktā.

Atvasinājuma fiziskā nozīme 1. Materiāla daļiņas ātruma noteikšanas uzdevums Ļaujiet punktam pārvietoties pa kādu taisni saskaņā ar likumu s= s(t), kur s ir nobrauktais attālums, t ir laiks, un ir jāatrod punkta ātrums momentā t0 . Līdz brīdim t0 nobrauktais attālums ir s0 = s(t0), un līdz laikam (t0 +∆t) ceļš ir s0 + ∆s=s(t0 +∆t). Tad intervālam ∆t vidējais ātrums būs Jo mazāks ∆t, jo labāk vidējais ātrums raksturo punkta kustību momentā t0. Tāpēc zem punkta ātrums laikā t0 jāsaprot vidējā ātruma robeža intervālam no t0 līdz t0 +∆t, kad ∆t⇾0 , t.i. 2. ĶĪMISKĀS REAKCIJAS ĀTRUMA PROBLĒMAĻaujiet kādai vielai iekļūt ķīmiskā reakcijā. Šīs vielas Q daudzums reakcijas laikā mainās atkarībā no laika t un ir laika funkcija. Ļaujiet vielas daudzumam mainīties par ∆Q laikā ∆t, tad attiecība izteiks vidējo ķīmiskās reakcijas ātrumu laikā ∆t, un šīs attiecības robeža ir ķīmiskās reakcijas ātrums noteiktā laikā. laiks t.

3. RADIOAKTĪVĀS SABRAUŽES ĀTRUMA NOTEIKŠANAS PROBLĒMA

Ja m ir radioaktīvās vielas masa un t ir laiks, tad radioaktīvās sabrukšanas parādību laikā t, ja radioaktīvās vielas masa laika gaitā samazinās, raksturo funkcija m = m(t).

Vidējo samazinājuma ātrumu laikā ∆t izsaka ar attiecību

un momentānās samazināšanās ātrumu laikā t

Funkcijas atvasinājuma fiziskā nozīme noteiktā punktā

Pamatelementārfunkciju atvasinājumi Diferenciācijas pamatlikumi Pieņemsim u=u(x) un v=v(x) - diferencējamas funkcijas punktā x. 1) (u  v) = u  v 2) (uv) = uv +uv (cu) = cu 3) , ja v  0

Funkcijas atvasinājums punktā ir diferenciālrēķina pamatjēdziens. Tas raksturo funkcijas izmaiņu ātrumu norādītajā punktā. Atvasinājumu plaši izmanto, risinot vairākas matemātikas, fizikas un citu zinātņu problēmas, īpaši pētot dažādu procesu ātrumu.

Pamatdefinīcijas

Atvasinājums ir vienāds ar funkcijas pieauguma un argumenta pieauguma attiecības robežu ar nosacījumu, ka pēdējam ir tendence uz nulli:

$y^(\prime)\left(x_(0)\right)=\lim _(\Delta x \rightarrow 0) \frac(\Delta y)(\Delta x)$

Definīcija

Tiek izsaukta funkcija, kurai kādā brīdī ir ierobežots atvasinājums diferencējams noteiktā punktā. Atvasinājuma aprēķināšanas process tiek saukts funkciju diferenciācija.

Vēstures atsauce

Krievu terminu "funkcijas atvasinājums" pirmo reizi izmantoja krievu matemātiķis V.I. Viskovatovs (1780 - 1812).

Pieauguma (argumenta/funkcijas) apzīmējumu ar grieķu burtu $\Delta$ (delta) pirmo reizi izmantoja Šveices matemātiķis un mehāniķis Johans Bernulli (1667-1748). Diferenciāļa apzīmējums, atvasinājums $d x$ pieder vācu matemātiķim G.V. Leibnics (1646 - 1716). Laika atvasinājuma apzīmēšanas veids ar punktu virs burta - $\dot(x)$ - nāk no angļu matemātiķa, mehāniķa un fiziķa Īzaka Ņūtona (1642 - 1727). Īsais atvasinājuma apzīmējums ar triepienu - $f^(\prime)(x)$ - pieder franču matemātiķim, astronomam un mehāniķim J.L. Lagranžs (1736 - 1813), kuru viņš ieviesa 1797. gadā. Daļēja atvasinājuma simbolu $\frac(\partial)(\partial x)$ savos darbos aktīvi izmantoja vācu matemātiķis Karls G.Ya. Jacobi (1805 - 1051), un pēc tam izcilais vācu matemātiķis Karls T.W. Veierštrāss (1815 - 1897), lai gan šis apzīmējums jau agrāk ir sastapts vienā no franču matemātiķa A.M. Leģenda (1752 - 1833). Diferenciāļa operatora simbolu $\nabla$ izgudroja izcilais īru matemātiķis, mehāniķis un fiziķis W.R. Hamiltons (1805 - 1865) 1853. gadā, un nosaukumu "nabla" ierosināja angļu pašmācības zinātnieks, inženieris, matemātiķis un fiziķis Olivers Hevisids (1850 - 1925) 1892. gadā.

Matemātikas nozari, kas pēta funkciju atvasinājumus un to lietojumus, sauc par diferenciālrēķinu. Šis aprēķins radās, risinot uzdevumus līkņu pieskares zīmēšanai, kustības ātruma aprēķināšanai, funkcijas lielāko un mazāko vērtību atrašanai.

Vairākas diferenciālrēķina problēmas senatnē atrisināja Arhimēds, izstrādājot pieskares zīmēšanas metodi. Arhimēds uzcēla pieskares spirālei, kas nes viņa vārdu. Arhimēds (ap 287. – 212. g. p.m.ē.) – izcils zinātnieks. Daudzu matemātikas un mehānikas faktu un metožu pionieris, izcils inženieris.

Funkcijas izmaiņu ātruma atrašanas problēmu pirmais atrisināja Ņūtons. Funkcijas izmaiņu ātruma atrašanas problēmu pirmais atrisināja Ņūtons. Viņš funkciju nosauca par fluent, t.i. pašreizējā vērtība. Atvasinājums - plūsma ar un e th. Viņš funkciju nosauca par fluent, t.i. pašreizējā vērtība. Atvasinājums - plūsma ar un e th. Ņūtons nāca klajā ar atvasinājuma jēdzienu, pamatojoties uz mehānikas jautājumiem. Īzaks Ņūtons (1643 - 1722) - angļu fiziķis un matemātiķis.

Pamatojoties uz Fermā rezultātiem un dažiem citiem secinājumiem, Leibnics 1684. gadā publicēja pirmo rakstu par diferenciālrēķinu, kurā izklāstīti diferenciācijas pamatnoteikumi. Leibnics Gotfrīds Frīdrihs (1646 - 1716) - izcilais vācu zinātnieks, filozofs, matemātiķis, fiziķis, jurists, valodnieks

Atvasinājuma pielietojums: Atvasinājuma pielietojums: 1) Jauda ir darba atvasinājums attiecībā pret laiku P \u003d A "(t). 2) Strāvas stiprums ir lādiņa atvasinājums attiecībā pret laiku I \u003d g" ( t). 3) Spēks ir nobīdes darba F \u003d A "(x) atvasinājums. 4) Siltuma jauda ir siltuma daudzuma atvasinājums attiecībā pret temperatūru C \u003d Q" (t). 5) Spiediens ir spēka atvasinājums attiecībā pret laukumu P \u003d F "(S) 6) Apkārtmērs ir apļa laukuma atvasinājums gar rādiusu l env \u003d S" cr (R). 7) Darba ražīguma pieauguma temps ir darba ražīguma laika atvasinājums. 8) Akadēmiskie panākumi? Zināšanu izaugsmes atvasinājums.

Atvasinājuma pielietojums fizikā Uzdevums: Divi ķermeņi pārvietojas pa taisnu, attiecīgi, saskaņā ar likumiem: S 1 (t) \u003d 3,5t 2 - 5t + 10 un S 2 (t) \u003d 1,5t 2 + 3t -6. Kurā brīdī ķermeņu ātrumi būs vienādi? Uzdevums: divi ķermeņi pārvietojas attiecīgi taisnā līnijā saskaņā ar likumiem: S 1 (t) \u003d 3,5t 2 - 5t + 10 un S 2 (t) \u003d 1,5t 2 + 3t -6. Kurā brīdī ķermeņu ātrumi būs vienādi?

Atvasinājuma pielietojums ekonomikā Problēma: Uzņēmums mēnesī saražo X vienības kāda viendabīga produkta. Konstatēts, ka uzņēmuma finansiālo ietaupījumu atkarība no produkcijas apjoma tiek izteikta ar formulu Uzdevums: Uzņēmums mēnesī saražo X vienības kādu viendabīgu produktu. Konstatēts, ka uzņēmuma finanšu ietaupījumu atkarība no produkcijas apjoma tiek izteikta ar formulu Izpētīt uzņēmuma potenciālu. Izpētiet uzņēmuma potenciālu. 15

Atvasinājuma jēdziena vēsture

Funkcijas, robežas, atvasinājums un integrālis ir matemātiskās analīzes pamatjēdzieni, kas tiek pētīti vidusskolā. Un atvasinājuma jēdziens ir nesaraujami saistīts ar funkcijas jēdzienu.

Terminu "funkcija" pirmo reizi ierosināja vācu filozofs un matemātiķis, lai raksturotu dažādus segmentus, kas savieno noteiktas līknes punktus 1692. gadā. Pirmā funkcijas definīcija, kas vairs nebija saistīta ar ģeometriskiem attēlojumiem, tika formulēta 1718. gadā. Johana Bernulli audzēknis

1748. gadā precizēja funkcijas definīciju. Eileram tiek piešķirts simbola f(x) ieviešana, lai apzīmētu funkciju.

Stingru funkcijas robežas un nepārtrauktības definīciju 1823. gadā formulēja franču matemātiķis. Augustīns Luiss Košī . Funkcijas nepārtrauktības definīciju vēl agrāk formulēja čehu matemātiķis Bernards Bolcāno. Saskaņā ar šīm definīcijām, pamatojoties uz reālo skaitļu teoriju, tika veikts matemātiskās analīzes galveno noteikumu stingrs pamatojums.

Pirms diferenciālrēķina pieeju un pamatu atklāšanas bija franču matemātiķa un jurista darbs, kurš 1629. gadā ierosināja metodes lielāko un mazāko funkciju vērtību noteikšanai, pieskares zīmēšanai patvaļīgām līknēm un faktiski paļāvās uz atvasinājumu izmantošana. To veicināja arī darbs, kas izstrādāja koordinātu metodi un analītiskās ģeometrijas pamatus. Tikai 1666. gadā un nedaudz vēlāk viņi neatkarīgi viens no otra izveidoja diferenciālrēķina teoriju. Ņūtons nonāca pie atvasinājuma jēdziena, risinot momentānā ātruma uzdevumus un , - aplūkojot ģeometrisko uzdevumu par līknes pieskares zīmēšanu. un pētīja funkciju maksimumu un minimumu problēmu.

Integrāļa aprēķins un pati integrāļa jēdziens radās no nepieciešamības aprēķināt plaknes figūru laukumus un patvaļīgu ķermeņu tilpumus. Integrālrēķina idejas rodas seno matemātiķu darbos. Taču tas liecina par Eudoksa "izsmelšanas metodi", ko viņš vēlāk izmantoja 3. gadsimtā. BC e Šīs metodes būtība bija tāda, ka, lai aprēķinātu plakanas figūras laukumu un, palielinot daudzstūra malu skaitu, viņi atrada robežu, kurā tika novirzīti pakāpju figūru laukumi. Tomēr katram skaitlim limita aprēķins bija atkarīgs no īpašas tehnikas izvēles. Un neatrisināta palika problēma par vispārējo skaitļu laukumu un apjomu aprēķināšanas metodi. Arhimēds vēl nepārprotami nepiemēroja vispārējo robežas un integrāļa jēdzienu, lai gan šie jēdzieni tika izmantoti netieši.

17. gadsimtā , kurš atklāja planētu kustības likumus, pirmais mēģinājums attīstīt idejas tika veiksmīgi veikts. Keplers aprēķināja plaknes figūru laukumus un ķermeņu tilpumus, pamatojoties uz ideju par figūras un ķermeņa sadalīšanu bezgalīgā skaitā bezgalīgi mazām daļām. Papildinājuma rezultātā šīs daļas sastāvēja no figūras, kuras laukums ir zināms un ļauj mums aprēķināt vēlamās platības. Matemātikas vēsturē iegāja tā sauktais "Kavaljē princips", ar kura palīdzību tika aprēķināti laukumi un tilpumi. Šis princips vēlāk teorētiski tika pamatots ar integrālrēķina palīdzību.
Citu zinātnieku idejas kļuva par augsni, uz kuras Ņūtons un Leibnics atklāja integrālrēķinu. Integrālrēķina attīstība turpinājās daudz vēlāk Pafnutijs Ļvovičs Čebiševs izstrādāja veidus, kā integrēt dažas iracionālo funkciju klases.

Mūsdienu integrāļa definīcija kā integrāļa summu robeža ir saistīta ar Košī. Simbols