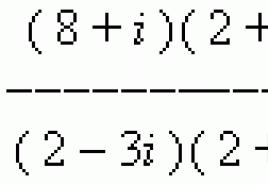Komplekso skaitļu teorija un piemēri. Kompleksie skaitļi
Kompleksie skaitļi
Iedomāts un kompleksie skaitļi. Abscisa un ordināta
kompleksais skaitlis. Konjugēt kompleksos skaitļus.
Darbības ar kompleksajiem skaitļiem. Ģeometriski
komplekso skaitļu attēlojums. sarežģīta plakne.
Kompleksa skaitļa modulis un arguments. trigonometrisks
kompleksā skaitļa forma. Operācijas ar kompleksu
cipari trigonometriskā formā. Moivre formula.
Pamatinformācija par iedomāts un kompleksie skaitļi ir doti sadaļā "Iedomātie un kompleksie skaitļi". Nepieciešamība pēc šiem jauna veida skaitļiem parādījās, risinot gadījuma kvadrātvienādojumus
D< 0 (здесь Dir kvadrātvienādojuma diskriminants). Ilgu laiku šie skaitļi neatrada fizisku pielietojumu, tāpēc tos sauca par "iedomātajiem" skaitļiem. Tomēr tagad tos ļoti plaši izmanto dažādās fizikas jomās.un tehnoloģija: elektrotehnika, hidro- un aerodinamika, elastības teorija utt.
Kompleksie skaitļi ir rakstīti šādi:a+bi. Šeit a un b – reāli skaitļi , a i – iedomātā vienība. e. i 2 = –1. Numurs a sauca abscisa, a b - ordinātakompleksais skaitlisa + b.Divi kompleksie skaitļia+bi un a-bi sauca konjugāts kompleksie skaitļi.
Galvenie līgumi:
1. Reālais skaitlis
avar rakstīt arī formākompleksais skaitlis:a + 0 i vai a - 0 i. Piemēram, ieraksti 5 + 0i un 5-0 inozīmē to pašu skaitli 5 .2. Komplekss skaitlis 0 + bisauca tīri iedomāts numuru. Ierakstīšanabinozīmē to pašu, ko 0 + bi.
3. Divi kompleksie skaitļia+bi unc+ditiek uzskatīti par vienādiem, jaa = c un b = d. Citādi kompleksie skaitļi nav vienādi.
Papildinājums. Komplekso skaitļu summaa+bi un c+disauc par komplekso skaitli (a+c ) + (b+d ) es .Pa šo ceļu, kad pievieno kompleksos skaitļus, to abscises un ordinātas pievieno atsevišķi.
Šī definīcija atbilst noteikumiem, kā rīkoties ar parastajiem polinomiem.
Atņemšana. Atšķirība starp diviem kompleksajiem skaitļiema+bi(samazināts) un c+di(atņemto) sauc par komplekso skaitli (a-c ) + (b-d ) es .
Pa šo ceļu, atņemot divus kompleksos skaitļus, to abscises un ordinātas tiek atņemtas atsevišķi.
Reizināšana. Komplekso skaitļu reizinājumsa+bi un c+di sauc par komplekso skaitli.
(ac-bd ) + (ad+bc ) es .Šī definīcija izriet no divām prasībām:
1) cipari a+bi un c+dijāreizina kā algebriski binomi,
2) numurs iir galvenais īpašums:i 2 = – 1.
PIEMĒRS ( a + bi )(a-bi) = a 2 +b 2 . Tāpēc strādāt
divi konjugēti kompleksie skaitļi ir vienādi ar reālo
pozitīvs skaitlis.
Divīzija. Sadaliet komplekso skaitlia+bi (dalāms) uz cituc+di(dalītājs) - nozīmē atrast trešo numurue + fi(tērzēšana), kas, reizinot ar dalītājuc+di, kā rezultātā tiek iegūta dividendea + b.
Ja dalītājs nav nulle, dalīšana vienmēr ir iespējama.
PIEMĒRS Atrast (8+i ) : (2 – 3 i) .
Risinājums. Pārrakstīsim šo attiecību kā daļskaitli:
Reizinot tā skaitītāju un saucēju ar 2 + 3i
UN pēc visu pārveidojumu veikšanas mēs iegūstam:

Komplekso skaitļu ģeometriskais attēlojums. Reālos skaitļus attēlo punkti uz skaitļu līnijas:
Šeit ir runa Anozīmē skaitli -3, punktsB ir skaitlis 2, un O- nulle. Turpretim kompleksos skaitļus attēlo punkti koordinātu plaknē. Šim nolūkam mēs izvēlamies taisnstūra (Dekarta) koordinātas ar vienādām skalām uz abām asīm. Tad kompleksais skaitlisa+bi tiks attēlots ar punktu P ar abscisu a un ordinātas b (skat. att.). Šo koordinātu sistēmu sauc sarežģīta plakne .

modulis komplekso skaitli sauc par vektora garumuOP, kas attēlo kompleksu skaitli uz koordinātas ( integrēta) lidmašīna. Kompleksā skaitļa modulisa+bi apzīmē ar | a+bi| vai vēstuli r
Nodarbības plāns.
1. Organizatoriskais moments.
2. Materiāla prezentācija.
3. Mājas darbs.
4. Nodarbības rezumēšana.
Nodarbību laikā
I. Organizatoriskais moments.
II. Materiāla prezentācija.
Motivācija.
Reālo skaitļu kopas paplašināšana sastāv no tā, ka reālajiem skaitļiem tiek pievienoti jauni (imaginārie) skaitļi. Šo skaitļu ieviešana ir saistīta ar neiespējamību iegūt sakni no negatīva skaitļa reālo skaitļu kopā.
Kompleksā skaitļa jēdziena ieviešana.
Iedomātos skaitļus, ar kuriem papildinām reālos skaitļus, raksta kā bi, kur i ir iedomātā vienība un i 2 = - 1.
Pamatojoties uz to, mēs iegūstam šādu kompleksā skaitļa definīciju.
Definīcija. Komplekss skaitlis ir formas izteiksme a+bi, kur a un b ir reāli skaitļi. Šajā gadījumā ir izpildīti šādi nosacījumi:
a) Divi kompleksie skaitļi a 1 + b 1 i un a 2 + b 2 i vienāds tad un tikai tad a 1 = a 2, b1=b2.
b) Komplekso skaitļu saskaitīšanu nosaka noteikums:
(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.
c) Komplekso skaitļu reizināšanu nosaka noteikums:
(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.
Kompleksa skaitļa algebriskā forma.
Kompleksā skaitļa ierakstīšana formā a+bi sauc par kompleksā skaitļa algebrisko formu, kur a- reālā daļa bi ir iedomātā daļa un b ir reāls skaitlis.
Komplekss skaitlis a+bi tiek uzskatīts par vienādu ar nulli, ja tā reālā un iedomātā daļa ir vienāda ar nulli: a=b=0
Komplekss skaitlis a+bi plkst b = 0 uzskatīts par reālu skaitli a: a + 0i = a.
Komplekss skaitlis a+bi plkst a = 0 sauc par tīri iedomātu un tiek apzīmēts bi: 0 + bi = bi.
Divi kompleksie skaitļi z = a + bi un = a – bi, kas atšķiras tikai ar iedomātās daļas zīmi, sauc par konjugātiem.
Darbības ar kompleksiem skaitļiem algebriskā formā.
Ar kompleksiem skaitļiem algebriskā formā var veikt šādas darbības.
1) Papildinājums.
Definīcija. Komplekso skaitļu summa z 1 = a 1 + b 1 i un z 2 = a 2 + b 2 i sauc par komplekso skaitli z, kuras reālā daļa ir vienāda ar reālo daļu summu z1 un z2, un iedomātā daļa ir skaitļu iedomāto daļu summa z1 un z2, tas ir z = (a 1 + a 2) + (b 1 + b 2) i.
Skaitļi z1 un z2 tiek saukti par terminiem.
Komplekso skaitļu saskaitīšanai ir šādas īpašības:
1º. Komutativitāte: z1 + z2 = z2 + z1.
2º. Asociativitāte: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).
3º. Komplekss skaitlis -a -bi sauc par pretstatu kompleksam skaitlim z = a + bi. Komplekss skaitlis, kas ir pretējs kompleksajam skaitlim z, apzīmēts -z. Komplekso skaitļu summa z un -z vienāds ar nulli: z + (-z) = 0
1. piemērs: Pievienot (3 - i) + (-1 + 2i).
(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
2) Atņemšana.
Definīcija. Atņemt no kompleksā skaitļa z1 kompleksais skaitlis z2 z, kas z + z 2 = z 1.
Teorēma. Komplekso skaitļu atšķirība pastāv un turklāt ir unikāla.
2. piemērs: atņemt (4 - 2i) - (-3 + 2i).
(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 - 4i.
3) Reizināšana.
Definīcija. Komplekso skaitļu reizinājums z 1 =a 1 + b 1 i un z 2 \u003d a 2 + b 2 i sauc par komplekso skaitli z, ko nosaka vienlīdzība: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1) i.
Skaitļi z1 un z2 sauc par faktoriem.
Komplekso skaitļu reizināšanai ir šādas īpašības:
1º. Komutativitāte: z 1 z 2 = z 2 z 1.
2º. Asociativitāte: (z 1 z 2) z 3 = z 1 (z 2 z 3)
3º. Reizināšanas sadalījums attiecībā uz saskaitīšanu:
(z 1 + z 2) z 3 \u003d z 1 z 3 + z 2 z 3.
4º. z \u003d (a + bi) (a - bi) \u003d a 2 + b 2 ir reāls skaitlis.
Praksē komplekso skaitļu reizināšanu veic saskaņā ar noteikumu, ka summa tiek reizināta ar summu un reālās un iedomātās daļas tiek atdalītas.
Nākamajā piemērā apsveriet komplekso skaitļu reizināšanu divos veidos: ar noteikumu un reizinot summu ar summu.
3. piemērs: reiziniet (2 + 3i) (5–7i).
1 veids. (2 + 3i) (5 - 7i) = (2 × 5 - 3 × (- 7)) + (2 × (- 7) + 3 × 5)i = = (10 + 21) + (- 14 + 15) )i = 31 + i.
2 virzienu. (2 + 3i) (5 - 7i) = 2 × 5 + 2 × (- 7i) + 3i × 5 + 3i × (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.
4) Sadalījums.
Definīcija. Sadaliet komplekso skaitli z1 uz kompleksu skaitli z2, nozīmē atrast šādu kompleksu skaitli z, kas z z 2 = z 1.
Teorēma. Komplekso skaitļu koeficients pastāv un ir unikāls, ja z2 ≠ 0 + 0i.
Praksē komplekso skaitļu koeficientu nosaka, reizinot skaitītāju un saucēju ar saucēja konjugātu.
Ļaujiet z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, tad



 .
.
Nākamajā piemērā mēs veicam dalīšanu pēc formulas un reizināšanas likumu ar saucēja konjugātu.
Piemērs 4. Atrodiet koeficientu  .
.
5) Paaugstināšana līdz pozitīvam veselam skaitlim.
a) Iedomātās vienotības spēki.
Izmantojot vienlīdzības priekšrocības i 2 \u003d -1, ir viegli definēt jebkuru iedomātās vienības pozitīvu veselu skaitļu jaudu. Mums ir:
i 3 \u003d i 2 i \u003d -i,
i 4 \u003d i 2 i 2 \u003d 1,
i 5 \u003d i 4 i \u003d i,
i 6 \u003d i 4 i 2 \u003d -1,
i 7 \u003d i 5 i 2 \u003d -i,
i 8 = i 6 i 2 = 1 utt.
Tas parāda, ka grādu vērtības es n, kur n- pozitīvs vesels skaitlis, kas periodiski atkārtojas, kad rādītājs palielinās par 4 .
Tāpēc, lai palielinātu skaitu i uz pozitīva vesela skaitļa pakāpju, dala eksponentu ar 4 un uzcelt i pakāpei, kuras eksponents ir dalījuma atlikums.
5. piemērs Aprēķiniet: (i 36 + i 17) i 23.
i 36 = (i 4) 9 = 1 9 = 1,
i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 i = i.
i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 i 3 = - i.
(i 36 + i 17) i 23 \u003d (1 + i) (- i) \u003d - i + 1 \u003d 1 - i.
b) Kompleksā skaitļa palielināšana līdz pozitīvam veselam skaitļa pakāpēm tiek veikta saskaņā ar likumu par binoma palielināšanu līdz atbilstošajam pakāpēm, jo tas ir īpašs identisku komplekso faktoru reizināšanas gadījums.
6. piemērs Aprēķiniet: (4 + 2i) 3
(4 + 2i) 3 = 4 3 + 3 × 4 2 × 2i + 3 × 4 × (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.
Kompleksie skaitļi ir minimāls mums pazīstamo reālo skaitļu kopas paplašinājums. To būtiskā atšķirība ir tāda, ka parādās elements, kas kvadrātā dod -1, t.i. es, vai .
Jebkurš komplekss skaitlis sastāv no divām daļām: reāls un iedomāts:
Tādējādi ir skaidrs, ka reālo skaitļu kopa sakrīt ar komplekso skaitļu kopu ar nulles iedomāto daļu.
Vispopulārākais komplekso skaitļu kopas modelis ir parastā plakne. Katra punkta pirmā koordināte būs tā reālā daļa, bet otrā - iedomātā. Tad pašu komplekso skaitļu loma būs vektoriem ar sākumu punktā (0,0).
Operācijas ar kompleksajiem skaitļiem.
Faktiski, ja ņemam vērā komplekso skaitļu kopas modeli, ir intuitīvi skaidrs, ka divu komplekso skaitļu saskaitīšana (atņemšana) un reizināšana tiek veikta tāpat kā atbilstošās darbības ar vektoriem. Turklāt mēs domājam vektoru krustojumu, jo šīs darbības rezultāts atkal ir vektors.
1.1 Papildinājums.
(Kā redzat, šī darbība precīzi atbilst )
1.2. Atņemšana, līdzīgi tiek veikta saskaņā ar šādu noteikumu:
2. Reizināšana.

3. Sadalījums.
To definē vienkārši kā reizināšanas apgriezto darbību.

trigonometriskā forma.
Kompleksā skaitļa z modulis ir šāds lielums:
 ,
,
ir skaidrs, ka tas atkal ir vienkārši vektora (a, b) modulis (garums).
Visbiežāk kompleksā skaitļa modulis tiek apzīmēts kā ρ.
Izrādās, ka
z = ρ(cosφ+isinφ).

Sekojošais tieši izriet no kompleksā skaitļa rakstīšanas trigonometriskās formas. formulas :
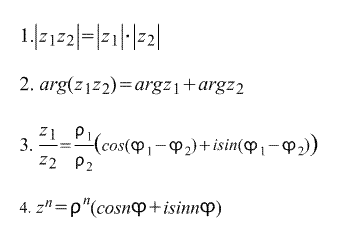
Pēdējā formula tiek saukta De Moivre formula. Formula ir iegūta tieši no tā. kompleksa skaitļa n-tā sakne:

tātad kompleksajam skaitlim z ir n-tās saknes.