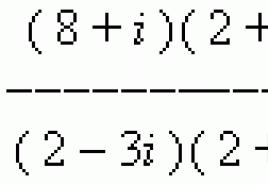Atrodiet leņķi starp diviem. Leņķis starp līnijām plaknē
Oi-oi-oi-oi... nu slinki, it kā teikumu pie sevis nolasītu =) Tomēr tad palīdzēs atslābums, jo īpaši tāpēc, ka šodien nopirku piemērotus aksesuārus. Tāpēc pāriesim pie pirmās sadaļas, es ceru, ka līdz raksta beigām es saglabāšu jautru noskaņojumu.
Divu taisnu līniju savstarpēja izkārtošanās
Gadījums, kad zāle dzied līdzi korī. Divas rindas var:
1) sērkociņš;
2) būt paralēli: ;
3) vai krustojas vienā punktā: .
Palīdzība manekeniem : lūdzu atcerieties krustojuma matemātisko zīmi , tā notiks ļoti bieži. Ieraksts nozīmē, ka līnija krustojas ar līniju punktā.
Kā noteikt divu līniju relatīvo stāvokli?
Sāksim ar pirmo gadījumu:
Divas līnijas sakrīt tad un tikai tad, ja to attiecīgie koeficienti ir proporcionāli, tas ir, ir tāds skaitlis "lambda", ka vienādības
Aplūkosim taisnes un no atbilstošajiem koeficientiem sastādīsim trīs vienādojumus: . No katra vienādojuma izriet, ka tāpēc šīs līnijas sakrīt.
Patiešām, ja visi vienādojuma koeficienti 
reizinot ar -1 (mainiet zīmes) un samazinot visus vienādojuma koeficientus ar 2, iegūstat to pašu vienādojumu: .
Otrais gadījums, kad līnijas ir paralēlas:
Divas taisnes ir paralēlas tad un tikai tad, ja to koeficienti pie mainīgajiem ir proporcionāli: 
, bet.
Piemēram, apsveriet divas taisnas līnijas. Mēs pārbaudām atbilstošo koeficientu proporcionalitāti mainīgajiem lielumiem: 
Tomēr ir skaidrs, ka.
Un trešais gadījums, kad līnijas krustojas:
Divas taisnes krustojas tad un tikai tad, ja to mainīgo koeficienti NAV proporcionāli, proti, NAV tādas "lambdas" vērtības, lai vienādības tiktu izpildītas 
Tātad taisnām līnijām mēs izveidosim sistēmu: 
No pirmā vienādojuma izriet, ka , un no otrā vienādojuma: , tātad, sistēma ir nekonsekventa(nav risinājumu). Tādējādi koeficienti pie mainīgajiem nav proporcionāli.
Secinājums: līnijas krustojas
Praktiskos uzdevumos var izmantot tikko aplūkoto risinājuma shēmu. Starp citu, tas ir ļoti līdzīgs vektoru kolinearitātes pārbaudes algoritmam, kuru mēs aplūkojām nodarbībā. Vektoru lineārās (ne)atkarības jēdziens. Vektoru pamats. Bet ir arī civilizētāka pakete:
1. piemērs
Uzziniet līniju relatīvo novietojumu: 
Risinājums pamatojoties uz taisnu līniju virzīšanas vektoru izpēti:
a) No vienādojumiem atrodam līniju virziena vektorus: 
.
, tāpēc vektori nav kolineāri un līnijas krustojas.
Katram gadījumam krustojumā nolikšu akmeni ar rādītājiem:
Pārējie lec pāri akmenim un seko tālāk, taisni uz Kaščeju bezmirstīgo =)
b) Atrodiet līniju virziena vektorus: 
Līnijām ir vienāds virziena vektors, kas nozīmē, ka tās ir paralēlas vai vienādas. Šeit determinants nav nepieciešams.
Acīmredzot nezināmo koeficienti ir proporcionāli, savukārt .
Noskaidrosim, vai vienlīdzība ir patiesa: 
Pa šo ceļu,
c) Atrodiet līniju virziena vektorus: 
Aprēķināsim determinantu, kas sastāv no šo vektoru koordinātām: 
, tāpēc virziena vektori ir kolineāri. Līnijas ir paralēlas vai sakrīt.
Proporcionalitātes koeficientu "lambda" ir viegli redzēt tieši no kolineāro virzienu vektoru attiecības. Tomēr to var atrast arī, izmantojot pašu vienādojumu koeficientus: 
.
Tagad noskaidrosim, vai vienlīdzība ir patiesa. Abi bezmaksas nosacījumi ir nulle, tāpēc:
Iegūtā vērtība apmierina šo vienādojumu (jebkurš skaitlis parasti to apmierina).
Tādējādi līnijas sakrīt.
Atbilde:
Ļoti drīz jūs iemācīsities (vai pat jau esat iemācījušies) atrisināt apdomāto problēmu verbāli burtiski dažu sekunžu laikā. Šajā sakarā es neredzu iemeslu piedāvāt kaut ko neatkarīgam risinājumam, labāk ir ielikt vēl vienu svarīgu ķieģeļu ģeometriskajā pamatnē:
Kā novilkt līniju, kas ir paralēla noteiktajai?
Par šī vienkāršākā uzdevuma nezināšanu Lakstīgala Laupītājs bargi soda.
2. piemērs
Taisni dod vienādojums . Uzrakstiet vienādojumu paralēlai taisnei, kas iet caur punktu.
Risinājums: Nezināmo rindu apzīmē ar burtu . Ko par to saka nosacījums? Līnija iet caur punktu. Un, ja taisnes ir paralēlas, tad ir acīmredzams, ka taisnes "ce" virzošais vektors ir piemērots arī taisnes "de" konstruēšanai.
Mēs izņemam virziena vektoru no vienādojuma:
Atbilde:
Piemēra ģeometrija izskatās vienkārša: 
Analītiskā pārbaude sastāv no šādām darbībām:
1) Pārbaudām, vai līnijām ir vienāds virziena vektors (ja taisnes vienādojums nav pareizi vienkāršots, tad vektori būs kolineāri).
2) Pārbaudiet, vai punkts apmierina iegūto vienādojumu.
Analītiskā pārbaude vairumā gadījumu ir viegli izdarāma mutiski. Apskatiet divus vienādojumus, un daudzi no jums ātri sapratīs, kā līnijas ir paralēlas bez zīmējuma.
Piemēri pašrisināšanai šodien būs radoši. Jo jums joprojām ir jāsacenšas ar Baba Yagu, un viņa, jūs zināt, ir visu veidu mīklu cienītāja.
3. piemērs
Uzrakstiet vienādojumu taisnei, kas iet caur punktu, kas ir paralēls taisnei if
Ir racionāls un ne pārāk racionāls risinājums. Īsākais ceļš ir nodarbības beigās.
Nedaudz pastrādājām ar paralēlām līnijām un pie tām atgriezīsimies vēlāk. Sakrītošo līniju gadījums ir maz interesants, tāpēc apskatīsim problēmu, kas jums ir labi zināma no skolas mācību programmas:
Kā atrast divu līniju krustošanās punktu?
Ja taisni 
krustojas punktā , tad tā koordinātas ir risinājums lineāro vienādojumu sistēmas 
Kā atrast līniju krustošanās punktu? Atrisiniet sistēmu.
Lūk, jums divu lineāru vienādojumu sistēmas ar diviem nezināmiem ģeometriskā nozīme ir divas plaknes krustojošas (visbiežāk) taisnes.
4. piemērs
Atrodiet līniju krustošanās punktu
Risinājums: Ir divi risināšanas veidi – grafiskais un analītiskais.
Grafiskais veids ir vienkārši uzzīmēt dotās līnijas un tieši no zīmējuma uzzināt krustošanās punktu: 
Šeit ir mūsu punkts: . Lai pārbaudītu, tās koordinātas jāievieto katrā taisnes vienādojumā, tām ir jāiekļaujas gan tur, gan tur. Citiem vārdiem sakot, punkta koordinātas ir sistēmas risinājums. Faktiski mēs apsvērām grafisku risinājumu lineāro vienādojumu sistēmas ar diviem vienādojumiem, diviem nezināmiem.
Grafiskā metode, protams, nav slikta, taču ir manāmi trūkumi. Nē, runa nav par to, ka septītklasnieki šādi izlemj, bet gan par to, ka pareiza un PRECĪZA zīmējuma uztaisīšana prasīs laiku. Turklāt dažas līnijas nav tik vienkārši konstruējamas, un pats krustošanās punkts var būt kaut kur trīsdesmitajā valstībā ārpus piezīmju grāmatiņas lapas.
Tāpēc krustošanās punktu lietderīgāk ir meklēt ar analītisko metodi. Atrisināsim sistēmu: 
Sistēmas risināšanai tika izmantota vienādojumu termiskās saskaitīšanas metode. Lai attīstītu attiecīgās prasmes, apmeklējiet nodarbību Kā atrisināt vienādojumu sistēmu?
Atbilde:
Pārbaude ir triviāla – krustojuma punkta koordinātām jāapmierina katrs sistēmas vienādojums.
5. piemērs
Atrodiet līniju krustošanās punktu, ja tās krustojas.
Šis ir “dari pats” piemērs. Uzdevumu var ērti sadalīt vairākos posmos. Stāvokļa analīze liecina, ka ir nepieciešams:
1) Uzrakstiet taisnas līnijas vienādojumu.
2) Uzrakstiet taisnes vienādojumu.
3) Noskaidro līniju relatīvo novietojumu.
4) Ja līnijas krustojas, tad atrodiet krustošanās punktu.
Darbības algoritma izstrāde ir raksturīga daudzām ģeometriskām problēmām, un es vairākkārt pievērsīšos tam.
Pilns risinājums un atbilde apmācības beigās:
Apavu pāris vēl nav nolietots, jo tikām pie otrās nodarbības sadaļas:
Perpendikulāras līnijas. Attālums no punkta līdz līnijai.
Leņķis starp līnijām
Sāksim ar tipisku un ļoti svarīgu uzdevumu. Pirmajā daļā mēs iemācījāmies izveidot taisni paralēli dotajai, un tagad būda uz vistu kājām pagriezīsies par 90 grādiem:
Kā novilkt līniju, kas ir perpendikulāra noteiktai?
6. piemērs
Taisni dod vienādojums . Uzrakstiet vienādojumu perpendikulārai taisnei, kas iet caur punktu.
Risinājums: Ir zināms, ka . Būtu jauki atrast taisnes virziena vektoru. Tā kā līnijas ir perpendikulāras, triks ir vienkāršs:
No vienādojuma “noņemam” normālvektoru: , kas būs taisnes virzošais vektors.
Mēs veidojam taisnas līnijas vienādojumu ar punktu un virziena vektoru:
Atbilde: 
Izvērsim ģeometrisko skici:
Hmm... Oranžas debesis, oranža jūra, oranžs kamielis.
Risinājuma analītiskā pārbaude:
1) Izvelciet no vienādojumiem virziena vektorus 
un ar palīdzību vektoru punktu reizinājums secinām, ka taisnes patiešām ir perpendikulāras: .
Starp citu, jūs varat izmantot parastos vektorus, tas ir vēl vienkāršāk.
2) Pārbaudiet, vai punkts apmierina iegūto vienādojumu 
.
Pārbaudi atkal ir viegli veikt mutiski.
7. piemērs
Atrodiet perpendikulāru līniju krustpunktu, ja vienādojums ir zināms 
un punkts.
Šis ir “dari pats” piemērs. Uzdevumā ir vairākas darbības, tāpēc ir ērti sakārtot risinājumu pa punktam.
Mūsu aizraujošais ceļojums turpinās:
Attālums no punkta līdz līnijai
Mūsu priekšā ir taisna upes josla, un mūsu uzdevums ir sasniegt to visīsākajā ceļā. Šķēršļu nav, un optimālākais maršruts būs kustība pa perpendikulu. Tas ir, attālums no punkta līdz līnijai ir perpendikulāra segmenta garums.
Attālums ģeometrijā tradicionāli tiek apzīmēts ar grieķu burtu "ro", piemēram: - attālums no punkta "em" līdz taisnei "de".
Attālums no punkta līdz līnijai 
tiek izteikts ar formulu
8. piemērs
Atrodiet attālumu no punkta līdz līnijai 
Risinājums: viss, kas jums nepieciešams, ir rūpīgi aizstāt skaitļus formulā un veikt aprēķinus:
Atbilde: 
Izpildīsim zīmējumu: 
Atrastais attālums no punkta līdz līnijai ir tieši sarkanā segmenta garums. Ja uz rūtainā papīra veido zīmējumu mērogā 1 vienība. \u003d 1 cm (2 šūnas), tad attālumu var izmērīt ar parastu lineālu.
Apsveriet citu uzdevumu saskaņā ar to pašu zīmējumu:
Uzdevums ir atrast punkta koordinātas, kas ir simetrisks punktam attiecībā pret taisni 
. Ierosinu darbības veikt patstāvīgi, tomēr risinājuma algoritmu izklāstīšu ar starprezultātiem:
1) Atrodiet taisni, kas ir perpendikulāra taisnei.
2) Atrodiet līniju krustošanās punktu: 
.
Abas darbības ir detalizēti apspriestas šajā nodarbībā.
3) Punkts ir segmenta viduspunkts. Mēs zinām vidus un viena gala koordinātas. Autors formulas segmenta vidusdaļas koordinātām atrast.
Nebūs lieki pārbaudīt, vai arī attālums ir vienāds ar 2,2 vienībām.
Šeit var rasties grūtības aprēķinos, bet tornī ļoti palīdz mikrokalkulators, kas ļauj saskaitīt parastās daļskaitļus. Daudzas reizes esmu ieteikusi un ieteikšu vēlreiz.
Kā atrast attālumu starp divām paralēlām līnijām?
9. piemērs
Atrodiet attālumu starp divām paralēlām līnijām
Šis ir vēl viens neatkarīga risinājuma piemērs. Neliels mājiens: ir bezgala daudz veidu, kā atrisināt. Apspriešana nodarbības beigās, bet labāk pamēģini uzminēt pats, manuprāt, tev izdevās labi izkliedēt savu atjautību.
Leņķis starp divām līnijām
Neatkarīgi no stūra, tad aploda: 
Ģeometrijā leņķis starp divām taisnēm tiek ņemts par MAZĀKO leņķi, no kura automātiski izriet, ka tas nevar būt neass. Attēlā sarkanā loka norādītais leņķis netiek uzskatīts par leņķi starp krustojošām līnijām. Un tā “zaļais” kaimiņš vai pretēji orientēts sārtināts stūrītis.
Ja līnijas ir perpendikulāras, par leņķi starp tām var uzskatīt jebkuru no 4 leņķiem.
Kā atšķiras leņķi? Orientēšanās. Pirmkārt, stūra "ritināšanas" virziens ir ļoti svarīgs. Otrkārt, negatīvi orientētu leņķi raksta ar mīnusa zīmi, piemēram, ja .
Kāpēc es to teicu? Šķiet, ka var iztikt ar ierasto leņķa jēdzienu. Fakts ir tāds, ka formulās, pēc kurām mēs atradīsim leņķus, var viegli iegūt negatīvu rezultātu, un tam nevajadzētu jūs pārsteigt. Leņķis ar mīnusa zīmi nav sliktāks, un tam ir ļoti specifiska ģeometriskā nozīme. Negatīvā leņķa zīmējumā obligāti jānorāda tā orientācija (pulksteņrādītāja virzienā) ar bultiņu.
Kā atrast leņķi starp divām līnijām? Ir divas darba formulas:
10. piemērs
Atrodiet leņķi starp līnijām
Risinājums un Pirmā metode
Apsveriet divas taisnas līnijas, kas dotas ar vienādojumiem vispārīgā formā: 
Ja taisni nav perpendikulāri, tad orientēts leņķi starp tiem var aprēķināt, izmantojot formulu: 
Pievērsīsim īpašu uzmanību saucējam - tieši tā skalārais produkts taisnu līniju virziena vektori:
Ja , tad formulas saucējs pazūd, un vektori būs ortogonāli un līnijas būs perpendikulāras. Tāpēc formulējumā tika izteikta atruna par līniju neperpendikularitāti.
Pamatojoties uz iepriekš minēto, risinājums ir ērti formalizēts divos posmos:
1) Aprēķiniet taisnu līniju virzīšanas vektoru skalāro reizinājumu:
tāpēc līnijas nav perpendikulāras.
2) Mēs atrodam leņķi starp līnijām pēc formulas:
Izmantojot apgriezto funkciju, ir viegli atrast pašu leņķi. Šajā gadījumā mēs izmantojam loka tangensa dīvainību (sk. Elementāro funkciju grafiki un īpašības):
Atbilde: 
Atbildē mēs norādām precīzu vērtību, kā arī aptuveno vērtību (vēlams gan grādos, gan radiānos), kas aprēķināta, izmantojot kalkulatoru.
Nu, mīnuss, tik mīnuss, tas ir labi. Šeit ir ģeometriska ilustrācija: 
Nav pārsteidzoši, ka leņķis izrādījās negatīvas orientācijas, jo uzdevuma stāvoklī pirmais skaitlis ir taisna līnija un tieši no tās sākās leņķa “vērpšanās”.
Ja jūs patiešām vēlaties iegūt pozitīvu leņķi, jums ir jāmaina taisnās līnijas, tas ir, jāņem koeficienti no otrā vienādojuma 
, un ņemt koeficientus no pirmā vienādojuma . Īsāk sakot, jums jāsāk ar tiešo 
.
Injekcija φ vispārīgie vienādojumi A 1 x + B 1 y + C 1 = 0 un A 2 x + B 2 y + C 2 = 0, aprēķina pēc formulas:
Injekcija φ starp divām taisnām līnijām kanoniskie vienādojumi(x-x 1) / m 1 \u003d (y-y 1) / n 1 un (x-x 2) / m 2 \u003d (y-y 2) / n 2, aprēķina pēc formulas:
Attālums no punkta līdz līnijai
Katru plakni telpā var attēlot kā lineāru vienādojumu, ko sauc vispārējais vienādojums lidmašīna
Īpaši gadījumi.
o Ja vienādojumā (8), tad plakne iet caur sākuma punktu.
o Ar (,) plakne ir attiecīgi paralēla asij (ass, ass).
o Kad (,) plakne ir paralēla plaknei (plakne, plakne).
Risinājums: izmantojiet (7)
Atbilde: plaknes vispārējais vienādojums.
Piemērs.
Plakne taisnstūra koordinātu sistēmā Oxyz tiek dota ar plaknes vispārīgo vienādojumu 
. Pierakstiet visu normālo vektoru koordinātas šajā plaknē.
Mēs zinām, ka mainīgo x, y un z koeficienti plaknes vispārējā vienādojumā ir atbilstošās šīs plaknes normālā vektora koordinātas. Tāpēc dotās plaknes normālvektors 
ir koordinātas. Visu normālo vektoru kopu var dot kā.
Uzrakstiet plaknes vienādojumu, ja taisnstūra koordinātu sistēmā Oxyz telpā tā iet caur punktu 
, a 
ir šīs plaknes normālais vektors.
Mēs piedāvājam divus šīs problēmas risinājumus.
No tā stāvokļa, kāds mums ir. Mēs aizstājam šos datus plaknes, kas iet caur punktu, vispārējā vienādojumā:
Uzrakstiet vispārīgo vienādojumu plaknei, kas ir paralēla koordinātu plaknei Oyz un iet caur punktu 
.
Plakni, kas ir paralēla koordinātu plaknei Oyz, var dot ar vispārīgu nepilnīgu formas plaknes vienādojumu. Kopš punkta 
pieder plaknei pēc nosacījuma, tad šī punkta koordinātēm ir jāapmierina plaknes vienādojums, tas ir, vienādībai ir jābūt patiesai. No šejienes mēs atrodam. Tādējādi vēlamajam vienādojumam ir forma.
Risinājums. Vektora reizinājums pēc definīcijas 10.26 ir ortogonāls vektoriem p un q. Tāpēc tas ir ortogonāls vēlamajai plaknei, un vektoru var uzskatīt par tā normālo vektoru. Atrodiet vektora n koordinātas:
tas ir 
. Izmantojot formulu (11.1), iegūstam
Atverot iekavas šajā vienādojumā, mēs nonākam pie galīgās atbildes.
Atbilde: 
.
Pārrakstīsim normālo vektoru formā un atradīsim tā garumu:
Saskaņā ar iepriekš minēto:
Atbilde: 
Paralēlām plaknēm ir vienāds normāls vektors. 1) No vienādojuma atrodam plaknes normālo vektoru:.
2) Plaknes vienādojumu veidojam pēc punkta un normālvektora: 
Atbilde:
Plaknes vektora vienādojums telpā
Plaknes parametriskais vienādojums telpā
Vienādojums plaknei, kas iet caur noteiktu punktu perpendikulāri noteiktam vektoram
Dota taisnstūra Dekarta koordinātu sistēma trīsdimensiju telpā. Formulēsim šādu problēmu:
Uzrakstiet vienādojumu plaknei, kas iet caur noteiktu punktu M(x 0, y 0, z 0) perpendikulāri dotajam vektoram n = ( A, B, C} .
Risinājums. Ļaujiet P(x, y, z) ir patvaļīgs punkts telpā. Punkts P pieder plaknei tad un tikai tad, ja vektors MP = {x − x 0, y − y 0, z − z 0) ortogonāli vektoram n = {A, B, C) (1. att.).
Uzrakstījis ortogonalitātes nosacījumu šiem vektoriem (n, MP) = 0 koordinātu formā, mēs iegūstam:
|
A(x − x 0) + B(y − y 0) + C(z − z 0) = 0 |
Plaknes vienādojums ar trim punktiem
Vektora formā
Koordinātās
Plakņu savstarpēja izkārtošanās telpā
ir divu plakņu vispārīgie vienādojumi. Pēc tam:
1) ja 
, tad plaknes sakrīt;
2) ja 
, tad plaknes ir paralēlas;
3) ja vai , tad plaknes krustojas un vienādojumu sistēma
(6)
ir doto plakņu krustošanās līnijas vienādojumi.
|
Risinājums: Mēs sastādām taisnās līnijas kanoniskos vienādojumus pēc formulas: Atbilde: |
Mēs ņemam iegūtos vienādojumus un garīgi “nospiežam”, piemēram, kreiso gabalu: . Tagad mēs pielīdzinām šo gabalu uz jebkuru numuru(atcerieties, ka jau bija nulle), piemēram, pret vienu: . Tā kā , tad pārējiem diviem "gabaliem" arī jābūt vienādiem ar vienu. Būtībā jums ir jāatrisina sistēma: |
Uzrakstiet parametru vienādojumus šādām rindām: 
Risinājums: Līnijas ir dotas ar kanoniskiem vienādojumiem un pirmajā posmā jāatrod kāds punkts, kas pieder pie taisnes un tās virziena vektora.
a) No vienādojumiem 
noņemt punktu un virziena vektoru: . Jūs varat izvēlēties citu punktu (kā to izdarīt, ir aprakstīts iepriekš), taču labāk ir izvēlēties visredzamāko. Starp citu, lai izvairītos no kļūdām, vienmēr vienādojumos aizstājiet tās koordinātas.
Sastādām šīs taisnes parametriskos vienādojumus: 
Parametrisko vienādojumu ērtība ir tāda, ka ar to palīdzību ir ļoti viegli atrast citus līnijas punktus. Piemēram, atradīsim punktu, kura koordinātas, teiksim, atbilst parametra vērtībai: 
Tādējādi: b) Aplūkosim kanoniskos vienādojumus 
. Punkta izvēle šeit ir vienkārša, bet mānīga: (uzmanieties, lai nesajauktu koordinātas!!!). Kā izvilkt virzošo vektoru? Varat spekulēt, kam šī līnija ir paralēla, vai arī varat izmantot vienkāršu formālu triku: proporcija ir “Y” un “Z”, tāpēc mēs rakstām virziena vektoru un atlikušajā vietā ievietojam nulli: .
Mēs sastādām taisnās līnijas parametriskos vienādojumus: 
c) Pārrakstīsim vienādojumus formā , tas ir, "Z" var būt jebkas. Un ja ir, tad ļaujiet, piemēram, . Tādējādi punkts pieder šai līnijai. Lai atrastu virziena vektoru, mēs izmantojam šādu formālu tehniku: sākotnējos vienādojumos ir "x" un "y", un virziena vektorā šajās vietās mēs rakstām nulles: . Atlikušajā vietā mēs ievietojam vienība: . Viena vietā derēs jebkurš skaitlis, izņemot nulli.
Mēs rakstām taisnās līnijas parametriskos vienādojumus: 
a. Dotas divas taisnes.Šīs līnijas, kā norādīts 1. nodaļā, veido dažādus pozitīvos un negatīvos leņķus, kas var būt gan akūti, gan neasi. Zinot vienu no šiem leņķiem, mēs varam viegli atrast jebkuru citu.
Starp citu, visiem šiem leņķiem pieskares skaitliskā vērtība ir vienāda, atšķirība var būt tikai zīmē
Līniju vienādojumi. Skaitļi ir pirmās un otrās taisnes virzošo vektoru projekcijas.Leņķis starp šiem vektoriem ir vienāds ar vienu no taisnes veidotajiem leņķiem. Tāpēc problēma tiek samazināta līdz leņķa noteikšanai starp vektoriem, mēs iegūstam
Vienkāršības labad varam vienoties par leņķi starp divām taisnēm, lai saprastu akūtu pozitīvu leņķi (kā, piemēram, 53. att.).
Tad šī leņķa tangensa vienmēr būs pozitīva. Tātad, ja formulas (1) labajā pusē tiek iegūta mīnusa zīme, tad tā ir jāatmet, t.i., jāsaglabā tikai absolūtā vērtība.
Piemērs. Nosakiet leņķi starp līnijām
Pēc formulas (1) mums ir
Ar. Ja norādīts, kura no leņķa malām ir tā sākums un kura beigas, tad, vienmēr skaitot leņķa virzienu pretēji pulksteņrādītāja virzienam, no formulām (1) varam izvilkt ko vairāk. Kā tas ir viegli redzams no att. 53 formulas (1) labajā pusē iegūtā zīme norādīs, kurš leņķis - akūts vai strups - veido otro līniju ar pirmo.
(Tiešām, no 53. attēla redzams, ka leņķis starp pirmo un otro virziena vektoru ir vai nu vienāds ar vēlamo leņķi starp līnijām, vai arī atšķiras no tā par ±180°.)
d. Ja taisnes ir paralēlas, tad paralēli ir arī to virziena vektori.Piemērojot divu vektoru paralēlisma nosacījumu, iegūstam!
Tas ir nepieciešams un pietiekams nosacījums, lai divas līnijas būtu paralēlas.
Piemērs. Tieša
ir paralēli, jo
e. Ja taisnes ir perpendikulāras, tad arī to virziena vektori ir perpendikulāri. Piemērojot divu vektoru perpendikulitātes nosacījumu, iegūstam divu taisnes perpendikulitātes nosacījumu, proti
Piemērs. Tieša
perpendikulāri, jo
Saistībā ar paralēlisma un perpendikularitātes nosacījumiem atrisināsim šādas divas problēmas.
f. Caur punktu novelciet līniju, kas ir paralēla noteiktai taisnei
Lēmums tiek pieņemts šādi. Tā kā vēlamā taisne ir paralēla dotajai, tad tās virziena vektoram varam ņemt to pašu, ko dotajai taisnei, ti, vektoru ar projekcijām A un B. Un tad tiks uzrakstīts vajadzīgās taisnes vienādojums formā (1. §)
Piemērs. Taisnes līnijas vienādojums, kas iet caur punktu (1; 3), kas ir paralēls taisnei
būs nākamais!
g. Novelciet līniju caur punktu, kas ir perpendikulārs dotajai līnijai
Šeit vairs neder ņemt vektoru ar projekcijām A un kā virzošo vektoru, bet ir jāuzvar tam perpendikulārs vektors. Tāpēc šī vektora projekcijas ir jāizvēlas saskaņā ar nosacījumu, ka abi vektori ir perpendikulāri, t.i., saskaņā ar nosacījumu
Šo nosacījumu var izpildīt bezgalīgi daudzos veidos, jo šeit ir viens vienādojums ar diviem nezināmajiem.Bet vienkāršākais veids ir to pieņemt.Tad vajadzīgās taisnes vienādojums tiks ierakstīts formā
Piemērs. Taisnes vienādojums, kas iet caur punktu (-7; 2) perpendikulārā taisnē
būs sekojošs (pēc otrās formulas)!
h. Gadījumā, ja līnijas ir dotas ar formas vienādojumiem
pārrakstot šos vienādojumus savādāk, mums ir
Definīcija. Ja divām līnijām ir dots y = k 1 x + b 1 , y = k 2 x + b 2 , tad akūto leņķi starp šīm līnijām definēs kā
Divas taisnes ir paralēlas, ja k 1 = k 2 . Divas taisnes ir perpendikulāras, ja k 1 = -1/ k 2 .
Teorēma. Taisnes līnijas Ax + Vy + C \u003d 0 un A 1 x + B 1 y + C 1 \u003d 0 ir paralēlas, ja koeficienti A 1 \u003d λA, B 1 \u003d λB ir proporcionāli. Ja arī С 1 = λС, tad līnijas sakrīt. Divu taisnu krustpunkta koordinātas tiek atrastas kā šo taisnu vienādojumu sistēmas risinājums.
Taisnes vienādojums, kas iet caur noteiktu punktu
Perpendikulāri šai līnijai
Definīcija. Taisni, kas iet caur punktu M 1 (x 1, y 1) un ir perpendikulāra taisnei y \u003d kx + b, attēlo vienādojums:
Attālums no punkta līdz līnijai
Teorēma. Ja ir dots punkts M(x 0, y 0), tad attālums līdz līnijai Ax + Vy + C \u003d 0 tiek definēts kā
.
Pierādījums. Pieņemsim, ka punkts M 1 (x 1, y 1) ir pamats perpendikulam, kas nomests no punkta M uz doto taisni. Tad attālums starp punktiem M un M 1:
(1)
Koordinātas x 1 un y 1 var atrast kā vienādojumu sistēmas risinājumu:
Otrais sistēmas vienādojums ir taisnes vienādojums, kas iet caur doto punktu M 0 perpendikulāri noteiktai taisnei. Ja mēs pārveidosim pirmo sistēmas vienādojumu formā:
A(x - x 0) + B(y - y 0) + Ax 0 + Ar 0 + C = 0,
tad, atrisinot, mēs iegūstam:
Aizvietojot šīs izteiksmes vienādojumā (1), mēs atrodam:
Teorēma ir pierādīta.
Piemērs. Nosakiet leņķi starp līnijām: y = -3 x + 7; y = 2 x + 1.
k 1 \u003d -3; k2 = 2; tgφ = 
; φ= p /4.
Piemērs. Parādiet, ka taisnes 3x - 5y + 7 = 0 un 10x + 6y - 3 = 0 ir perpendikulāras.
Risinājums. Mēs atrodam: k 1 \u003d 3/5, k 2 \u003d -5/3, k 1 * k 2 \u003d -1, tāpēc līnijas ir perpendikulāras.
Piemērs. Dotas trijstūra A(0; 1), B (6; 5), C (12; -1) virsotnes. Atrodiet augstuma vienādojumu, kas novilkts no virsotnes C.
Risinājums. Mēs atrodam malas AB vienādojumu: 
; 4 x = 6 y - 6;
2x – 3y + 3 = 0;
Vēlamais augstuma vienādojums ir: Ax + By + C = 0 vai y = kx + b. k = . Tad y = . Jo augstums iet caur punktu C, tad tā koordinātas atbilst šim vienādojumam: 
kur b = 17. Kopā: . 
Atbilde: 3x + 2y - 34 = 0.
Taisnes vienādojums, kas iet caur noteiktu punktu noteiktā virzienā. Taisnes līnijas vienādojums, kas iet caur diviem dotiem punktiem. Leņķis starp divām līnijām. Divu taisnes paralēlisma un perpendikulitātes nosacījums. Divu taisnju krustpunkta noteikšana
1. Taisnes vienādojums, kas iet caur noteiktu punktu A(x 1 , y 1) noteiktā virzienā, ko nosaka slīpums k,
y - y 1 = k(x - x 1). (1)
Šis vienādojums definē līniju zīmuli, kas iet caur punktu A(x 1 , y 1), ko sauc par stara centru.
2. Taisnas līnijas vienādojums, kas iet caur diviem punktiem: A(x 1 , y 1) un B(x 2 , y 2) ir rakstīts šādi:
Taisnes līnijas slīpumu, kas iet caur diviem dotajiem punktiem, nosaka pēc formulas
3. Leņķis starp taisnām līnijām A un B ir leņķis, par kādu jāpagriež pirmā taisne A ap šo līniju krustpunktu pretēji pulksteņrādītāja virzienam, līdz tas sakrīt ar otro līniju B. Ja ar slīpuma vienādojumiem dotas divas taisnes
y = k 1 x + B 1 ,
y = k 2 x + B 2 , (4)
tad leņķi starp tiem nosaka pēc formulas
Jāņem vērā, ka daļas skaitītājā pirmās taisnes slīpums tiek atņemts no otrās taisnes slīpuma.
Ja taisnes vienādojumi ir doti vispārīgā formā
A 1 x + B 1 y + C 1 = 0,
A 2 x + B 2 y + C 2 = 0, (6)
leņķi starp tiem nosaka pēc formulas
4. Divu līniju paralēlisma nosacījumi:
a) Ja taisnes ir dotas vienādojumos (4) ar slīpumu, tad nepieciešamais un pietiekams nosacījums to paralēlismam ir to slīpumu vienādība:
k 1 = k 2 . (8)
b) Gadījumā, ja taisnes ir dotas ar vienādojumiem vispārīgā formā (6), to paralēlismam nepieciešamais un pietiekams nosacījums ir tas, ka koeficienti pie atbilstošajām strāvas koordinātām to vienādojumos ir proporcionāli, t.i.
5. Divu līniju perpendikulitātes nosacījumi:
a) Gadījumā, ja taisnes ir dotas vienādojumos (4) ar slīpumu, nepieciešamais un pietiekams nosacījums to perpendikularitātei ir, ka to slīpumi ir apgriezti pēc lieluma un pretējas pēc zīmes, t.i.
Šo nosacījumu var ierakstīt arī formā
k 1 k 2 = -1. (11)
b) Ja taisnu vienādojumi ir doti vispārīgā formā (6), tad to perpendikulitātes nosacījums (nepieciešams un pietiekams) ir izpildīt vienādību
A 1 A 2 + B 1 B 2 = 0. (12)
6. Divu taisnu krustpunkta koordinātas tiek atrastas, atrisinot vienādojumu sistēmu (6). Līnijas (6) krustojas tad un tikai tad
1. Uzrakstiet vienādojumus taisnēm, kas iet caur punktu M, no kurām viena ir paralēla, bet otra ir perpendikulāra dotajai taisnei l.
\(\blacktriangleright\) Divstūra leņķis ir leņķis, ko veido divas pusplaknes un taisne \(a\) , kas ir to kopējā robeža.
\(\blacktriangleright\) Lai atrastu leņķi starp plaknēm \(\xi\) un \(\pi\) , jāatrod lineārais leņķis pikants vai taisni) no divšķautņu leņķa, ko veido plaknes \(\xi\) un \(\pi\):
1. darbība: pieņemsim \(\xi\cap\pi=a\) (plakņu krustošanās līnija). Plaknē \(\xi\) atzīmējam patvaļīgu punktu \(F\) un uzzīmējam \(FA\perp a\) ;
2. darbība: uzzīmējiet \(FG\perp \pi\) ;
3. solis: saskaņā ar TTP (\(FG\) - perpendikulāri, \(FA\) - slīpi, \(AG\) - projekcija) mums ir: \(AG\perp a\) ;
4. solis: leņķi \(\angle FAG\) sauc par divskaldņa leņķa lineāro leņķi, ko veido plaknes \(\xi\) un \(\pi\) .
Ņemiet vērā, ka trīsstūris \(AG\) ir taisnleņķa trīsstūris.
Ņemiet vērā arī to, ka plakne \(AFG\), kas konstruēta šādā veidā, ir perpendikulāra abām plaknēm \(\xi\) un \(\pi\) . Tāpēc to var teikt citā veidā: leņķis starp plaknēm\(\xi\) un \(\pi\) ir leņķis starp divām krustojošām līnijām \(c\in \xi\) un \(b\in\pi\), kas veido plakni, kas ir perpendikulāra \(\xi\ ) un \(\pi\) .
1. uzdevums #2875
Uzdevuma līmenis: grūtāks nekā eksāmens
Dota četrstūra piramīda, kuras visas malas ir vienādas un pamatne ir kvadrāts. Atrodiet \(6\cos \alpha\) , kur \(\alpha\) ir leņķis starp blakus esošajām sānu malām.
Pieņemsim, ka \(SABCD\) ir dota piramīda (\(S\) ir virsotne), kuras malas ir vienādas ar \(a\) . Tāpēc visas sānu malas ir vienādi vienādmalu trīsstūri. Atrodiet leņķi starp skaldnēm \(SAD\) un \(SCD\) .
Uzzīmēsim \(CH\perp SD\) . Jo \(\trijstūris SAD=\trijstūris SCD\), tad \(AH\) būs arī augstums \(\trīsstūris SAD\) . Tāpēc pēc definīcijas \(\angle AHC=\alpha\) ir lineārais divskaldnis leņķis starp skaldnēm \(SAD\) un \(SCD\) .
Tā kā bāze ir kvadrāts, tad \(AC=a\sqrt2\) . Ņemiet vērā arī to, ka \(CH=AH\) ir vienādmalu trīsstūra augstums ar malu \(a\) , tātad \(CH=AH=\frac(\sqrt3)2a\) .
Tad ar kosinusa teorēmu no \(\trijstūris AHC\): \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]
Atbilde: -2
2. uzdevums #2876
Uzdevuma līmenis: grūtāks nekā eksāmens
Plaknes \(\pi_1\) un \(\pi_2\) krustojas leņķī, kura kosinuss ir vienāds ar \(0,2\) . Plaknes \(\pi_2\) un \(\pi_3\) krustojas taisnā leņķī, un plakņu \(\pi_1\) un \(\pi_2\) krustošanās līnija ir paralēla plaknes \(\pi_2\) un \(\ pi_3\) . Atrodiet sinusu leņķim starp plaknēm \(\pi_1\) un \(\pi_3\) .
Lai \(\pi_1\) un \(\pi_2\) krustošanās līnija ir līnija \(a\) , \(\pi_2\) un \(\pi_3\) krustošanās līnija ir līnija \ (b\) , un krustojuma līnija \(\pi_3\) un \(\pi_1\) ir taisne \(c\) . Tā kā \(a\parallel b\) , tad \(c\parallel a\parallel b\) (saskaņā ar teorēmu no teorētiskās atsauces sadaļas "Ģeometrija telpā" \(\rightarrow\) "Ievads stereometrijā, paralēlisms”).
Atzīmējiet punktus \(A\in a, B\in b\) tā, lai \(AB\perp a, AB\perp b\) (tas ir iespējams, jo \(a\paralēlie b\) ). Atzīmējiet \(C\in c\), lai \(BC\perp c\) , tātad \(BC\perp b\) . Pēc tam \(AC\perp c\) un \(AC\perp a\) .
Patiešām, tā kā \(AB\perp b, BC\perp b\) , tad \(b\) ir perpendikulāra plaknei \(ABC\) . Tā kā \(c\parallel a\parallel b\) , tad arī līnijas \(a\) un \(c\) ir perpendikulāras plaknei \(ABC\) un līdz ar to jebkura līnija no šīs plaknes, jo īpaši, līnija \ (AC\) .
No tā izriet, ka \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\), \(\angle BCA=\angle (\pi_3, \pi_1)\). Izrādās, ka \(\trijstūris ABC\) ir taisnstūrveida, kas nozīmē \[\sin \angle BCA=\cos \angle BAC=0,2.\]
Atbilde: 0.2
3. uzdevums #2877
Uzdevuma līmenis: grūtāks nekā eksāmens
Dotas līnijas \(a, b, c\), kas krustojas vienā punktā, un leņķis starp jebkurām divām no tām ir vienāds ar \(60^\circ\) . Atrodiet \(\cos^(-1)\alpha\) , kur \(\alpha\) ir leņķis starp plakni, ko veido līnijas \(a\) un \(c\), un plakni, ko veido līnijas \(b\ ) un \(c\) . Sniedziet atbildi grādos.
Ļaujiet taisnēm krustoties punktā \(O\) . Tā kā leņķis starp jebkurām divām no tām ir vienāds ar \(60^\circ\) , tad visas trīs līnijas nevar atrasties vienā plaknē. Atzīmēsim punktu \(A\) uz līnijas \(a\) un uzzīmēsim \(AB\perp b\) un \(AC\perp c\) . Tad \(\trijstūris AOB=\trijstūris AOC\) kā taisnstūrveida hipotenūzā un akūtā leņķī. Tādējādi \(OB=OC\) un \(AB=AC\) .
Darīsim \(AH\perp (BOC)\) . Tad ar trīs perpendikulu teorēmu \(HC\perp c\) , \(HB\perp b\) . Kopš \(AB=AC\) , tad \(\trijstūris AHB=\trijstūris AHC\) kā taisnstūrveida gar hipotenūzu un kāju. Tāpēc \(HB=HC\) . Tādējādi \(OH\) ir leņķa \(BOC\) bisektrise (jo punkts \(H) atrodas vienādā attālumā no leņķa malām).
Ņemiet vērā, ka šādā veidā esam konstruējuši arī divskaldņa leņķa lineāro leņķi, ko veido plakne, ko veido taisnes \(a\) un \(c\), un plakne, ko veido līnijas \(b\) un \( c\) . Šis ir leņķis \(ACH\) .
Atradīsim šo stūrīti. Tā kā punktu \(A\) izvēlējāmies patvaļīgi, tad izvēlēsimies to tā, lai \(OA=2\) . Pēc tam taisnstūrveida formā \(\trīsstūris AOC\): \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ] Tā kā \(OH\) ir bisektrise, tad \(\angle HOC=30^\circ\) , tāpēc taisnstūrveida formā \(\trīsstūris HOC\): \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Pēc tam no taisnstūra \(\trijstūris ACH\): \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]
Atbilde: 3
4. uzdevums #2910
Uzdevuma līmenis: grūtāks nekā eksāmens
Plaknes \(\pi_1\) un \(\pi_2\) krustojas pa taisni \(l\) , kurā ir punkti \(M\) un \(N\) . Segmenti \(MA\) un \(MB\) ir perpendikulāri līnijai \(l\) un atrodas attiecīgi plaknēs \(\pi_1\) un \(\pi_2\) un \(MN = 15) \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Atrodiet \(3\cos\alpha\) , kur \(\alpha\) ir leņķis starp plaknēm \(\pi_1\) un \(\pi_2\) .
Trijstūris \(AMN\) ir taisnleņķis, \(AN^2 = AM^2 + MN^2\) , no kurienes \ Trijstūris \(BMN\) ir taisnleņķis, \(BN^2 = BM^2 + MN^2\) , no kurienes \ Mēs rakstām kosinusa teorēmu trijstūrim \(AMB\): \ Tad \ Tā kā leņķis \(\alpha\) starp plaknēm ir akūts leņķis un \(\angle AMB\) izrādījās neass, tad \(\cos\alpha=\dfrac5(12)\) . Tad \
Atbilde: 1.25
5. uzdevums #2911
Uzdevuma līmenis: grūtāks nekā eksāmens
\(ABCDA_1B_1C_1D_1\) ir paralēlskaldnis, \(ABCD\) ir kvadrāts ar malu \(a\) , punkts \(M\) ir pamats perpendikulam, kas nomests no punkta \(A_1\) uz plakni \ ((ABCD)\) , turklāt \(M\) ir kvadrāta \(ABCD\) diagonāļu krustpunkts. Ir zināms, ka \(A_1M = \dfrac(\sqrt(3))(2)a\). Atrodiet leņķi starp plaknēm \((ABCD)\) un \((AA_1B_1B)\) . Sniedziet atbildi grādos.
Mēs konstruējam \(MN\) perpendikulāri \(AB\), kā parādīts attēlā.
Tā kā \(ABCD\) ir kvadrāts ar malu \(a\) un \(MN\perp AB\) un \(BC\perp AB\) , tad \(MN\paralēli BC\) . Tā kā \(M\) ir kvadrāta diagonāļu krustpunkts, tad \(M\) ir \(AC\) viduspunkts, tāpēc \(MN\) ir viduslīnija un \(MN=\frac12BC=\frac(1)(2)a\).
\(MN\) ir \(A_1N\) projekcija uz plakni \((ABCD)\) , un \(MN\) ir perpendikulāra \(AB\) , tad, izmantojot trīs perpendikulu teorēmu, \( A_1N\) ir perpendikulāra \(AB \), un leņķis starp plaknēm \((ABCD)\) un \((AA_1B_1B)\) ir \(\angle A_1NM\) .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]
Atbilde: 60
6. uzdevums #1854
Uzdevuma līmenis: grūtāks nekā eksāmens
Kvadrātiņā \(ABCD\) : \(O\) ir diagonāļu krustošanās punkts; \(S\) neatrodas kvadrāta plaknē, \(SO \perp ABC\) . Atrodiet leņķi starp plaknēm \(ASD\) un \(ABC\), ja \(SO = 5\) un \(AB = 10\) .
Taisnstūra trīsstūri \(\trijstūris SAO\) un \(\trijstūris SDO\) ir vienādi divās malās un leņķis starp tiem (\(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = 90^\circ\); \(AO = DO\) , jo \(O\) ir kvadrāta diagonāļu krustpunkts, \(SO\) ir kopējā mala) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\trijstūris ASD\) ir vienādsānu. Punkts \(K\) ir \(AD\) viduspunkts, tad \(SK\) ir augstums trīsstūrī \(\trijstūris ASD\) un \(OK\) ir augstums trīsstūrī \ (AOD\) \(\ Rightarrow\) plakne \(SOK\) ir perpendikulāra plaknēm \(ASD\) un \(ABC\) \(\Rightarrow\) \(\angle SKO\) ir lineārs leņķis, kas vienāds līdz vajadzīgajam divskaldņa leņķim.
\(\trijstūris SKO\) : \(Labi = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\trijstūris SOK\) ir vienādsānu taisnstūra trīsstūris \(\Rightarrow\) \(\angle SKO = 45^\circ\) .
Atbilde: 45
7. uzdevums #1855
Uzdevuma līmenis: grūtāks nekā eksāmens
Kvadrātiņā \(ABCD\) : \(O\) ir diagonāļu krustošanās punkts; \(S\) neatrodas kvadrāta plaknē, \(SO \perp ABC\) . Atrodiet leņķi starp plaknēm \(ASD\) un \(BSC\), ja \(SO = 5\) un \(AB = 10\) .
Taisnstūra trīsstūri \(\trijstūris SAO\) , \(\trijstūris SDO\) , \(\trijstūris SOB\) un \(\trijstūris SOC\) ir vienādi divās malās un leņķis starp tiem (\(SO \perp ABC) \) \(\bultiņa pa labi\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\) , jo \(O\) ir kvadrāta diagonāļu krustpunkts, \(SO\) ir kopējā mala) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightbult\) \(\trijstūris ASD\) un \(\trijstūris BSC\) ir vienādsānu. Punkts \(K\) ir \(AD\) viduspunkts, tad \(SK\) ir augstums trīsstūrī \(\trijstūris ASD\) un \(OK\) ir augstums trīsstūrī \ (AOD\) \(\ bultiņa pa labi\) plakne \(SOK\) ir perpendikulāra plaknei \(ASD\) . Punkts \(L\) ir \(BC\) viduspunkts, tad \(SL\) ir augstums trīsstūrī \(\trijstūris BSC\) un \(OL\) ir augstums trīsstūrī \ (BOC\) \(\ bultiņa pa labi\) plakne \(SOL\) (aka plakne \(SOK\) ) ir perpendikulāra plaknei \(BSC\) . Tādējādi mēs iegūstam, ka \(\angle KSL\) ir lineārs leņķis, kas vienāds ar vēlamo divvirsmas leņķi.
\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Labā bultiņa\) \(OL = 5\) ; \(SK = SL\) - augstumi vienādsānu trīsstūros, ko var atrast, izmantojot Pitagora teorēmu: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). To var redzēt \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)' 90^\ circ\) .
Atbilde: 90
Studentu sagatavošana matemātikas eksāmenam, kā likums, sākas ar pamatformulu atkārtošanu, ieskaitot tās, kas ļauj noteikt leņķi starp plaknēm. Neskatoties uz to, ka šī ģeometrijas sadaļa ir pietiekami detalizēti apskatīta skolas mācību programmas ietvaros, daudziem absolventiem ir jāatkārto pamatmateriāls. Saprotot, kā atrast leņķi starp plaknēm, vidusskolēni uzdevuma risināšanas gaitā varēs ātri aprēķināt pareizo atbildi un rēķināties ar pienācīgu punktu skaitu, pamatojoties uz vienoto valsts eksāmenu.
Galvenās nianses
Lai jautājums par to, kā atrast divskaldņa leņķi, nesagādātu grūtības, iesakām sekot risinājuma algoritmam, kas palīdzēs tikt galā ar eksāmena uzdevumiem.
Vispirms jums ir jānosaka līnija, pa kuru plaknes krustojas.
Tad uz šīs līnijas jums jāizvēlas punkts un jānovelk divi perpendiķi tam.
Nākamais solis ir atrast diedrālā leņķa trigonometrisko funkciju, ko veido perpendikuli. Visērtāk to izdarīt, izmantojot iegūto trīsstūri, kura daļa ir stūris.
Atbilde būs leņķa vērtība vai tā trigonometriskā funkcija.
Sagatavošanās eksāmenam kopā ar Shkolkovo ir jūsu panākumu atslēga
Mācību procesā eksāmena nokārtošanas priekšvakarā daudzi studenti saskaras ar problēmu atrast definīcijas un formulas, kas ļauj aprēķināt leņķi starp 2 plaknēm. Skolas mācību grāmata ne vienmēr ir pie rokas tieši tad, kad tā ir vajadzīga. Un, lai atrastu nepieciešamās formulas un piemērus to pareizai pielietošanai, tostarp leņķa atrašanai starp plaknēm internetā, dažreiz jums ir jāpavada daudz laika.
Matemātikas portāls "Shkolkovo" piedāvā jaunu pieeju, gatavojoties valsts eksāmenam. Nodarbības mūsu vietnē palīdzēs studentiem pašiem noteikt vissarežģītākās sadaļas un aizpildīt nepilnības zināšanās.
Esam sagatavojuši un skaidri uzrādījuši visu nepieciešamo materiālu. Pamatdefinīcijas un formulas ir sniegtas sadaļā "Teorētiskā atsauce".
Lai labāk apgūtu materiālu, iesakām praktizēt arī atbilstošos vingrinājumus. Plašs dažādas sarežģītības pakāpes uzdevumu klāsts, piemēram, uz, ir parādīts sadaļā Katalogs. Visi uzdevumi satur detalizētu algoritmu pareizās atbildes atrašanai. Vietnes vingrinājumu saraksts tiek pastāvīgi papildināts un atjaunināts.
Praktizējoties problēmu risināšanā, kurās nepieciešams atrast leņķi starp divām plaknēm, studentiem ir iespēja tiešsaistē saglabāt jebkuru uzdevumu "Izlases". Pateicoties tam, viņi varēs atgriezties pie viņa nepieciešamo reižu skaitu un apspriest viņa risinājuma gaitu ar skolas skolotāju vai skolotāju.
