Methods for specifying a function - Knowledge Hypermarket. Concept of function

Specifying a function means specifying a rule that allows you to find for each argument value the corresponding function value. There are three main ways to specify functions: analytical, tabular and graphical.

Analytical method of specifying a function

is that the correspondence between and is given by formulas, for example,

Tabular method of specifying a function

The function can be specified using tables that indicate some variable values and the corresponding variable values. These tables can be obtained both directly from experience and with the help of certain mathematical calculations.

Graphical way to specify a function

In the practice of physical measurements, another method of specifying functions is used - graphical, in which the correspondence between the independent and dependent variables is specified using a graph, usually recorded with special instruments.

Implicit function assignment

Consideration of another way to specify a function, the so-called implicit function definition, is associated with the concept of an equation with two variables.

Consider the equation

Let there be a set such that for every number there is at least one number that satisfies the equation.

Let's denote one of these numbers by and put it in correspondence with the number . As a result, we obtain a function defined on the set and such that

In this case, they say that the function is specified implicitly by the equation. This equation specifies, generally speaking, not one, but a number of functions.

So, a function is called implicit if it is given by an equation with two variables that is unresolved with respect to . In contrast, a function defined by an equation with two variables, resolved with respect to , is called explicit.

The term “implicit function” does not reflect the nature of the functional dependence, but only the way it is specified. The same function can be specified both explicitly and implicitly. For example, functions

The main ways of specifying functions are given: explicit analytical; interval; parametric; implicit; specifying a function using a series; tabular; graphic. Examples of application of these methods

Content

An explicit analytical way to specify a function

At in an explicit way, the value of the function is determined by the formula representing the equation y = f (x). On the left side of this equation is the dependent variable y, and on the right is an expression made up of the independent variable x, constants, known functions and the operations of addition, subtraction, multiplication and division. Known functions are elementary functions and special functions, the values of which can be calculated using computer technology.

Here are some examples of explicitly specifying a function with an independent variable x and a dependent variable y:
;
;
.

Interval method of specifying a function

At interval method of specifying a function, the domain of definition is divided into several intervals, and the function is specified separately for each interval.

Here are some examples of the interval method of specifying a function:

Parametric method of specifying a function

At parametric method, a new variable is introduced, which is called a parameter. Next, set the values of x and y as a function of the parameter, using the explicit setting method:
(1)

Here are examples of the parametric way of specifying a function using the t parameter:

The advantage of the parametric method is that the same function can be specified in an infinite number of ways. For example, a function can be defined like this:

Or you can do this:

This freedom of choice, in some cases, allows you to use this method to solve equations (see “Differential equations that do not contain one of the variables”). The essence of the application is that we substitute two functions and instead of the variables x and y into the equation. Then we set one of them at our own discretion, so that the other can be determined from the resulting equation.

This method is also used to simplify calculations. For example, the dependence of the coordinates of the points of an ellipse with semi-axes a and b can be represented as follows:
.
In parametric form, this dependence can be given a simpler form:
.

Equations (1) are not the only way to specify a function parametrically. You can enter not one, but several parameters, connecting them with additional equations. For example, you can enter two parameters and . Then the function definition will look like this:

Here an additional equation appears that relates the parameters. If the number of parameters is n , then there must be n - 1 additional equations.

An example of the use of several parameters is presented on the page “Jacobi Differential Equation”. There the solution is sought in the following form:
(2) .
The result is a system of equations. To solve it, a fourth parameter t is introduced. After solving the system, three equations are obtained that relate the four parameters and .

Implicit way to specify a function

At in an implicit way, the value of the function is determined from the solution of the equation.

For example, the equation of an ellipse is:
(3) .
It's a simple equation. If we consider only the top part of the ellipse, , then we can express the variable y as a function of x in an explicit way:
(4) .
But even if it is possible to reduce (3) to an explicit way of specifying function (4), the latter formula is not always convenient to use. For example, to find the derivative, it is convenient to differentiate equation (3) rather than (4):
;
.

Setting a function nearby

An extremely important way to define a function is to series representation, composed of known functions. This method allows you to study a function using mathematical methods and calculate its values for applied problems.

The most common representation is to define a function using a power series. A number of functions are used:
.
The series with negative degrees is also used:
.
For example, the sine function has the following expansion:
(5) .
Such expansions are widely used in computing because they make it possible to reduce calculations to arithmetic operations.

As an illustration, let's calculate the value of the sine of 30° using expansion (5).
Converting degrees to radians:
.
We substitute in (5):

.

In mathematics, along with power series, expansions into trigonometric series in functions and , as well as in other special functions, are widely used. Using series, you can make approximate calculations of integrals, equations (differential, integral, partial derivatives) and study their solutions.

Tabular method of specifying a function

At tabular method of specifying a function we have a table that contains the values of the independent variable x and the corresponding values of the dependent variable y. The independent and dependent variables may have different notations, but we use x and y here. To determine the value of a function for a given value x, we use the table to find the value x closest to ours. After this, we determine the corresponding value of the dependent variable y.

To more accurately determine the value of the function, we assume that the function between two adjacent values of x is linear, that is, it has the following form:
.
Here are the function values found from the table, with the corresponding argument values.
Let's look at an example. Let us need to find the value of the function at . From the table we find:
.
Then

.
Exact value:
.
From this example it is clear that the use of linear approximation led to increased accuracy in determining the value of the function.

The tabular method is used in applied sciences. Before the development of computer technology, it was widely used in engineering and other calculations. Now the tabular method is used in statistics and experimental sciences for collecting and analyzing experimental data.

Graphical way to specify a function

At graphically, the value of the function is determined from a graph, the values of the independent variable are plotted along the abscissa axis, and the dependent variable is plotted along the ordinate axis.

The graphical method gives a visual representation of the behavior of the function. The results of a function study are often illustrated with a graph. From the graph you can determine the approximate value of the function. This allows you to use the graphical method in applied and engineering calculations.

Analytical method of specifying a function.

The most universal and powerful way. A function defined analytically this is the function that is given formulas. Actually, this is the whole explanation.) Functions that are familiar to everyone (I want to believe!), for example: y = 2x, or y = x 2 etc. and so on. are specified analytically.

By the way, not every formula can define a function. Not every formula meets the strict condition from the definition of a function. Namely - for every X there can only be one igrek. For example, in the formula y = ±x, For one values x=2, it turns out two y values: +2 and -2. This formula cannot define a unique function. As a rule, they don’t work with multi-valued functions in this branch of mathematics, in calculus.

What is good about the analytical way of specifying a function? Because if you have a formula, you know about the function All! You can make a sign. Build a graph. Explore this feature in full. Predict exactly where and how this function will behave. All mathematical analysis is based on this method of specifying functions. Let's say, taking a derivative of a table is extremely difficult...)

The analytical method is quite familiar and does not create problems. Perhaps there are some variations of this method that students encounter. I'm talking about parametric and implicit functions.) But such functions are in a special lesson.

Let's move on to less familiar ways of specifying a function.

Tabular method of specifying a function.

As the name suggests, this method is a simple sign. In this table, each x corresponds to ( is put in accordance) some meaning of the game. The first line contains the values of the argument. The second line contains the corresponding function values, for example:

Table 1.

x	- 3	- 1	0	2	3	4
y	5	2	- 4	- 1	6	5

Please pay attention! In this example, the game depends on X anyhow. I came up with this on purpose.) There is no pattern. It's okay, it happens. Means, exactly I have specified this specific function. Exactly I established a rule according to which an X turns into a Y.

You can make up another a plate containing a pattern. This sign will indicate other function, for example:

Table 2.

x	- 3	- 1	0	2	3	4
y	- 6	- 2	0	4	6	8

Did you catch the pattern? Here all the values of the game are obtained by multiplying x by two. Here is the first “tricky” question: can a function defined using Table 2 be considered a function y = 2x? Think for now, the answer will be below, in a graphical way. It's all very clear there.)

What's good tabular method of specifying a function? Yes, because you don’t need to count anything. Everything has already been calculated and written in the table.) But there is nothing more good. We don't know the value of the function for X's, which are not in the table. In this method, such x values are simply does not exist. By the way, this is a hint to a tricky question.) We cannot find out how the function behaves outside the table. We can't do anything. And the clarity of this method leaves much to be desired... The graphical method is good for clarity.

Graphical way to specify a function.

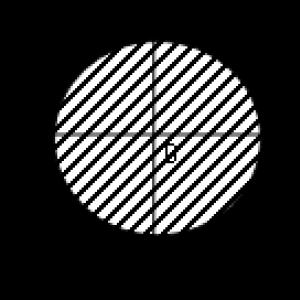
In this method, the function is represented by a graph. The argument (x) is plotted along the abscissa axis, and the function value (y) is plotted along the ordinate axis. According to the schedule, you can also choose any X and find the corresponding value at. The graph can be any, but... not just any one.) We work only with unambiguous functions. The definition of such a function clearly states: each X is put in accordance the only one at. One one game, not two, or three... For example, let's look at the circle graph:

A circle is like a circle... Why shouldn't it be the graph of a function? Let's find which game will correspond to the value of X, for example, 6? We move the cursor over the graph (or touch the drawing on the tablet), and... we see that this x corresponds two game meanings: y=2 and y=6.

Two and six! Therefore, such a graph will not be a graphical assignment of the function. On one x accounts for two game. This graph does not correspond to the definition of a function.

But if the unambiguity condition is met, the graph can be absolutely anything. For example:

This same crookedness is the law by which an X can be converted into a Y. Unambiguous. We wanted to know the meaning of the function for x = 4, For example. We need to find the four on the x-axis and see which game corresponds to this x. We move the mouse over the figure and see that the function value at For x=4 equals five. We don’t know what formula determines this transformation of an X into a Y. And it is not necessary. Everything is set by the schedule.

Now we can return to the “tricky” question about y=2x. Let's plot this function. Here he is:

Of course, when drawing this graph we did not take an infinite number of values X. We took several values and calculated y, made a sign - and everything is ready! The most literate people took only two values of X! And rightly so. For a straight line you don’t need more. Why the extra work?

But we knew for sure what x could be anyone. Integer, fractional, negative... Any. This is according to the formula y=2x it is seen. Therefore, we boldly connected the points on the graph with a solid line.

If the function is given to us by Table 2, then we will have to take the values of x only from the table. Because other X's (and Y's) are not given to us, and there is nowhere to get them. These values are not present in this function. The schedule will work out from points. We move the mouse over the figure and see the graph of the function specified in Table 2. I didn’t write the x-y values on the axes, you’ll figure it out, cell by cell?)

Here is the answer to the “tricky” question. Function specified by Table 2 and function y=2x - different.

The graphical method is good for its clarity. You can immediately see how the function behaves, where it increases. where it decreases. From the graph you can immediately find out some important characteristics of the function. And in the topic with derivatives, tasks with graphs are all over the place!

In general, analytical and graphical methods of defining a function go hand in hand. Working with the formula helps to build a graph. And the graph often suggests solutions that you wouldn’t even notice in the formula... We will be friends with graphs.)

Almost any student knows the three ways to define a function that we just looked at. But to the question: “And the fourth!?” - freezes thoroughly.)

There is such a way.

Verbal description of the function.

Yes Yes! The function can be quite unambiguously specified in words. The great and mighty Russian language is capable of a lot!) Let's say the function y=2x can be specified with the following verbal description: Each real value of the argument x is associated with its double value. Like this! The rule is established, the function is specified.

Moreover, you can verbally specify a function that is extremely difficult, if not impossible, to define using a formula. For example: Each value of the natural argument x is associated with the sum of the digits that make up the value of x. For example, if x=3, That y=3. If x=257, That y=2+5+7=14. And so on. It is problematic to write this down in a formula. But the sign is easy to make. And build a schedule. By the way, the graph looks funny...) Try it.

The method of verbal description is quite exotic. But sometimes it does. I brought it here to give you confidence in unexpected and unusual situations. You just need to understand the meaning of the words "function specified..." Here it is, this meaning:

If there is a law of one-to-one correspondence between X And at- that means there is a function. What law, in what form it is expressed - a formula, a tablet, a graph, words, songs, dances - does not change the essence of the matter. This law allows you to determine the corresponding value of the Y from the value of X. All.

Now we will apply this deep knowledge to some non-standard tasks.) As promised at the beginning of the lesson.

Exercise 1:

The function y = f(x) is given by Table 1:

Table 1.

Find the value of the function p(4), if p(x)= f(x) - g(x)

If you can’t understand what’s what at all, read the previous lesson “What is a function?” It is written very clearly about such letters and brackets.) And if only the tabular form confuses you, then we’ll sort it out here.

From the previous lesson it is clear that if, p(x) = f(x) - g(x), That p(4) = f(4) - g(4). Letters f And g means the rules according to which each X is assigned its own game. For each letter ( f And g) - yours rule. Which is given by the corresponding table.

Function value f(4) determined from Table 1. This will be 5. Function value g(4) determined according to Table 2. This will be 8. The most difficult thing remains.)

p(4) = 5 - 8 = -3

This is the correct answer.

Solve the inequality f(x) > 2

That's it! It is necessary to solve the inequality, which (in the usual form) is brilliantly absent! The only thing left to do is either give up the task or use your head. We choose the second and discuss.)

What does it mean to solve inequality? This means finding all the values of x at which the condition given to us is satisfied f(x) > 2. Those. all function values ( at) must be greater than two. And on our chart we have every game... And there are more twos, and less... And let’s, for clarity, draw a border along this two! We move the cursor over the drawing and see this border.

Strictly speaking, this boundary is the graph of the function y=2, but that's not the point. The important thing is that now the graph shows very clearly where, at what X's, function values, i.e. y, more than two. They are more X > 3. At X > 3 our whole function passes higher borders y=2. That's the solution. But it’s too early to turn off your head!) I still need to write down the answer...

The graph shows that our function does not extend left and right to infinity. The points at the ends of the graph indicate this. The function ends there. Therefore, in our inequality, all the X’s that go beyond the limits of the function have no meaning. For the function of these X's does not exist. And we, in fact, solve the inequality for the function...

The correct answer will be:

3 < X ≤ 6

Or, in another form:

X ∈ (3; 6]

Now everything is as it should be. Three is not included in the answer, because the original inequality is strict. And the six turns on, because and the function at six exists, and the inequality condition is satisfied. We have successfully solved an inequality that (in the usual form) does not exist...

This is how some knowledge and elementary logic saves you in non-standard cases.)

Analytical function assignment

Function %%y = f(x), x \in X%% is given in an explicit analytical way, if given a formula indicating the sequence of mathematical operations that must be performed with the argument %%x%% in order to obtain the value %%f(x)%% of this function.

Example

%% y = 2 x^2 + 3x + 5, x \in \mathbb(R)%%;
%% y = \frac(1)(x - 5), x \neq 5%%;
%% y = \sqrt(x), x \geq 0%%.

So, for example, in physics, with uniformly accelerated rectilinear motion, the speed of a body is determined by the formula %%v = v_0 + a t%%, and the formula for moving %%s%% of a body with uniformly accelerated motion over the time interval from %%0%% to %% t%% is written as: %% s = s_0 + v_0 t + \frac(a t^2)(2) %%.

Piecewise defined functions

Sometimes the function in question can be specified by several formulas that operate in different parts of its domain of definition, in which the argument of the function changes. For example: $$ y = \begin(cases) x ^ 2,~ if~x< 0, \\ \sqrt{x},~ если~x \geq 0. \end{cases} $$

Functions of this type are sometimes called composite or piecewise specified. An example of such a function is %%y = |x|%%

Function Domain

If a function is specified in an explicit analytical way using a formula, but the domain of definition of the function in the form of a set %%D%% is not specified, then by %%D%% we will always mean the set of values of the argument %%x%% for which this formula makes sense . So for the function %%y = x^2%% the domain of definition is the set %%D = \mathbb(R) = (-\infty, +\infty)%%, since the argument %%x%% can take any values on number line. And for the function %%y = \frac(1)(\sqrt(1 - x^2))%% the domain of definition will be the set of values %%x%% satisfying the inequality %%1 - x^2 > 0%%, t .e. %%D = (-1, 1)%%.

Advantages of explicitly specifying a function analytically

Note that the explicit analytical method of specifying a function is quite compact (the formula, as a rule, takes up little space), is easy to reproduce (the formula is not difficult to write) and is most suitable for performing mathematical operations and transformations on functions.

Some of these operations - algebraic (addition, multiplication, etc.) - are well known from the school mathematics course, others (differentiation, integration) will be studied in the future. However, this method is not always clear, since the nature of the function’s dependence on the argument is not always clear, and sometimes cumbersome calculations are required to find the function values (if they are necessary).

Implicit function assignment

Function %%y = f(x)%% defined in an implicit analytical way, if the relation $$F(x,y) = 0 is given, ~~~~~~~~~~(1)$$ connecting the values of the function %%y%% and the argument %%x%%. If you specify the values of the argument, then to find the value of %%y%% corresponding to a specific value of %%x%%, you need to solve the equation %%(1)%% for %%y%% at this specific value of %%x%%.

Given the value %%x%%, the equation %%(1)%% may have no solution or have more than one solution. In the first case, the specified value %%x%% does not belong to the domain of definition of the implicitly specified function, and in the second case it specifies multivalued function, which has more than one meaning for a given argument value.

Note that if the equation %%(1)%% can be explicitly resolved with respect to %%y = f(x)%%, then we obtain the same function, but already specified in an explicit analytical way. So, the equation %%x + y^5 - 1 = 0%%

and the equality %%y = \sqrt(1 - x)%% define the same function.

Parametric function specification

When the dependence of %%y%% on %%x%% is not given directly, but instead the dependences of both variables %%x%% and %%y%% on some third auxiliary variable %%t%% are given in the form

$$ \begin(cases) x = \varphi(t),\\ y = \psi(t), \end(cases) ~~~t \in T \subseteq \mathbb(R), ~~~~~ ~~~~~(2) $$what they talk about parametric method of specifying the function;

then the auxiliary variable %%t%% is called a parameter.

If it is possible to eliminate the parameter %%t%% from the equations %%(2)%%, then we arrive at a function defined by the explicit or implicit analytical dependence of %%y%% on %%x%%. For example, from the relations $$ \begin(cases) x = 2 t + 5, \\ y = 4 t + 12, \end(cases), ~~~t \in \mathbb(R), $$ except for the % parameter %t%% we obtain the dependence %%y = 2 x + 2%%, which defines a straight line in the %%xOy%% plane.

Graphic method

Example of a graphical function definition

The above examples show that the analytical method of specifying a function corresponds to its graphic image, which can be considered as a convenient and visual form of describing a function. Sometimes used graphic method specifying a function when the dependence of %%y%% on %%x%% is specified by a line on the plane %%xOy%%. However, despite all the clarity, it loses in accuracy, since the values of the argument and the corresponding function values can be obtained from the graph only approximately. The resulting error depends on the scale and accuracy of measurement of the abscissa and ordinate of individual points on the graph. In the future, we will assign the function graph only the role of illustrating the behavior of the function and therefore we will limit ourselves to constructing “sketches” of graphs that reflect the main features of the functions.

Tabular method

Note tabular method function assignments, when some argument values and the corresponding function values are placed in a table in a certain order. This is how well-known tables of trigonometric functions, tables of logarithms, etc. are constructed. The relationship between quantities measured in experimental studies, observations, and tests is usually presented in the form of a table.

The disadvantage of this method is that it is impossible to directly determine function values for argument values not included in the table. If there is confidence that the argument values not presented in the table belong to the domain of definition of the function in question, then the corresponding function values can be approximately calculated using interpolation and extrapolation.

Example

x	3	5.1	10	12.5
y	9	23	80	110

Algorithmic and verbal methods of specifying functions

The function can be set algorithmic(or software) in a way that is widely used in computer calculations.

Finally, it can be noted descriptive(or verbal) a way to specify a function, when the rule for matching the function values to the argument values is expressed in words.

For example, the function %%[x] = m~\forall (x \in )