Taisnas līnijas vienādojumam segmentos ir forma. Taisnas līnijas vienādojums segmentos - apraksts, piemēri, problēmu risināšana

Mēs turpinām pētīt sadaļu “Taisnes līnijas vienādojums plaknē” un šajā rakstā analizēsim tēmu “Taisnes līnijas vienādojums segmentos”. Secīgi aplūkosim taisnes vienādojuma formu nogriežņos, taisnes uzbūvi, ko dod šis vienādojums, pāreju no vispārējā taisnes vienādojuma uz taisnes vienādojumu posmos. Tam visam tiks pievienoti piemēri un problēmu risināšanas analīze.

Taisnstūra koordinātu sistēma O x y atrodas plaknē.

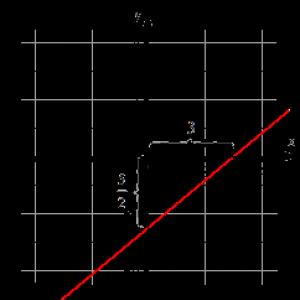
Taisni uz plaknes Dekarta koordinātu sistēmā O xy dod vienādojums formā xa + yb = 1 , kur a un b ir daži reāli skaitļi, kas nav nulle un kuru vērtības ir vienādas ar segmentu garumiem. nogriezta ar taisnu līniju uz asīm O x un O y . Segmentu garumi tiek ņemti vērā no koordinātu sākuma.

Kā mēs zinām, jebkura taisnei piederoša punkta koordinātas, kas norādītas ar taisnes vienādojumu, apmierina šīs taisnes vienādojumu. Punkti a , 0 un 0 , b pieder šai taisnei, jo a a + 0 b = 1 ⇔ 1 ≡ 1 un 0 a + b b = 1 ⇔ 1 ≡ 1 . Punkti a , 0 un b , 0 atrodas uz koordinātu asīm O x un O y un tiek noņemti no sākuma ar a un b vienībām. Virzienu, kurā vēlaties atlikt segmenta garumu, nosaka zīme, kas atrodas pirms cipariem a un b. Zīme “-” nozīmē, ka segmenta garums ir jāatzīmē koordinātu ass negatīvajā virzienā.

Izskaidrosim visu iepriekš minēto, shematiskā zīmējumā novietojot līnijas attiecībā pret fiksētu Dekarta koordinātu sistēmu O x y. Taisnes vienādojumu posmos x a + y b = 1 izmanto, lai izveidotu taisni Dekarta koordinātu sistēmā O x y . Lai to izdarītu, uz asīm jāatzīmē punkti a, 0 un b, 0 un pēc tam jāsavieno šie punkti ar līniju, izmantojot lineālu.

Zīmējumā parādīti gadījumi, kad skaitļiem a un b ir dažādas zīmes, un tāpēc segmentu garumi ir attēloti dažādos koordinātu asu virzienos.

Apsveriet piemēru.

1. piemērs

Taisni uzrāda taisnes vienādojums segmentos formā x 3 + y - 5 2 = 1 . Šo taisni nepieciešams uzbūvēt uz plaknes Dekarta koordinātu sistēmā O x y .

Risinājums

Izmantojot taisnes vienādojumu segmentos, mēs nosakām punktus, caur kuriem iet taisne. Tas ir 3 0 0 - 5 2 . Atzīmēsim tos un novelsim līniju.

Taisnes vispārīgā vienādojuma reducēšana uz taisnes vienādojumu segmentos

Pāreja no dotā taisnes vienādojuma uz taisnes vienādojumu segmentos atvieglo dažādu uzdevumu risināšanu. Ja ir pilns taisnes vispārīgais vienādojums, mēs varam iegūt taisnes vienādojumu segmentos.

Pilnīgajam plaknes taisnes vienādojumam ir forma A x + B y + C = 0, kur A, B un C nav vienādi ar nulli. Skaitli C pārnesam uz vienādības labo pusi, abas iegūtās vienādības daļas sadalām ar - C. Vienlaikus nosūtām uz saucējiem x un y koeficientus:

A x + B y + C = 0 ⇔ A x + B y = - C ⇔ ⇔ A - C x + B - C y = 1 ⇔ x - C A + y - C B = 1

Lai īstenotu pēdējo pāreju, mēs izmantojām vienādību p q = 1 q p , p ≠ 0, q ≠ 0.

Rezultātā esam veikuši pāreju no taisnes A x + B y + C = 0 vispārējā vienādojuma uz taisnes vienādojumu posmos xa + yb = 1 , kur a = - CA , b = - CB.

Apskatīsim šādu piemēru.

2. piemērs

Veiksim pāreju uz taisnes vienādojumu segmentos, kam ir taisnes vispārīgais vienādojums x - 7 y + 1 2 = 0 .

Risinājums

Mēs pārnesam vienu sekundi uz vienādības x - 7 y + 1 2 = 0 ⇔ x - 7 y = - 1 2 labo pusi.

Sadaliet abas vienādojuma puses ar - 1 2: x - 7 y = - 1 2 ⇔ 1 - 1 2 x - 7 - 1 2 y = 1 .

Pārveidosim iegūto vienādību vēlamajā formā: 1 - 1 2 x - 7 - 1 2 y = 1 ⇔ x - 1 2 + y 1 14 = 1 .

Mēs esam ieguvuši taisnas līnijas vienādojumu segmentos.

Atbilde: x - 1 2 + y 1 14 = 1

Gadījumos, kad taisne tiek dota ar kanonisku vai parametrisku taisnes vienādojumu plaknē, tad vispirms pārejam pie vispārīgā taisnes vienādojuma, bet pēc tam pie taisnes vienādojuma posmos.

Pārejot no taisnes vienādojuma segmentos un taisnes vispārīgā vienādojuma ir vienkāršs: mēs pārnesam vienību no taisnes vienādojuma labās puses formas xa + yb \u003d 1 segmentos uz kreiso pusi. pusē ar pretējo zīmi, mēs izvēlamies koeficientus nezināmo x un y priekšā.

x a + y b = 1 ⇔ x a + y b - 1 = 0 ⇔ 1 a x + 1 b y - 1 = 0

Iegūstam vispārīgo taisnes vienādojumu, no kura varam pāriet uz jebkuru citu plaknes taisnes vienādojuma formu. Mēs detalizēti analizējām pārejas procesu tēmā “Taisnes vispārējā vienādojuma reducēšana uz citiem taisnes vienādojuma veidiem”.

3. piemērs

Taisnas līnijas vienādojumam segmentos ir forma x 2 3 + y - 12 = 1. Ir nepieciešams uzrakstīt plaknē taisnes vispārīgo vienādojumu.

Risinājums

Tas darbojas saskaņā ar iepriekš aprakstīto algoritmu:

x 2 3 + y - 12 = 1 ⇔ 1 2 3 x + 1 - 12 y - 1 = 0 ⇔ ⇔ 3 2 x - 1 12 y - 1 = 0

Atbilde: 3 2 x - 1 12 y - 1 = 0

Ja pamanāt tekstā kļūdu, lūdzu, iezīmējiet to un nospiediet Ctrl+Enter

Taisnas līnijas vienādojums , kur a un b tiek izsaukti daži reāli skaitļi, kas nav nulles taisnas līnijas vienādojums segmentos. Šis nosaukums nav nejaušs, jo ir skaitļu absolūtās vērtības a un b vienāds ar to segmentu garumiem, kurus taisne nogriež uz koordinātu asīm Vērsis un Oy attiecīgi (segmenti tiek skaitīti no sākuma). Tādējādi taisnas līnijas vienādojums segmentos ļauj viegli izveidot šo taisni zīmējumā. Lai to izdarītu, plaknē atzīmējiet punktus ar koordinātām un taisnstūra koordinātu sistēmā, un izmantojiet lineālu, lai savienotu tos ar taisnu līniju.

Piemēram, izveidosim taisnu līniju, kas norādīta ar vienādojumu formas segmentos. Atzīmējiet punktus un savienojiet tos.

Sīkāku informāciju par šāda veida taisnes vienādojumu plaknē varat iegūt raksta vienādojumā par taisnēm segmentos.

Lapas augšdaļa

Darba beigas -

Šī tēma pieder:

Algebra un analītiskā ģeometrija. Matricas jēdziens, operācijas ar matricām un to īpašības

Matricas operāciju jēdziens ar matricām un to īpašības .. matrica ir taisnstūrveida tabula, kas sastāv no skaitļiem, kurus nevar .. un matricas pievienošana ir elementu darbība.

Ja jums ir nepieciešams papildu materiāls par šo tēmu vai jūs neatradāt to, ko meklējāt, mēs iesakām izmantot meklēšanu mūsu darbu datubāzē:

Ko darīsim ar saņemto materiālu:

Ja šis materiāls jums izrādījās noderīgs, varat to saglabāt savā lapā sociālajos tīklos:

čivināt

Visas tēmas šajā sadaļā:

Atšķirības definīcija
Atvasinājuma atrašanas darbību sauc par funkcijas diferenciāciju. Tiek uzskatīts, ka funkcija kādā brīdī ir diferencējama, ja tai tajā brīdī ir ierobežots atvasinājums, un

Diferenciācijas noteikums
Secinājums 1. Konstanto koeficientu var izņemt no atvasinājuma zīmes:

Atvasinājuma ģeometriskā nozīme. Pieskares vienādojums
Taisnas līnijas slīpuma leņķis y \u003d kx + b ir leņķis, ko mēra no pozīcijas

Funkcijas atvasinājuma ģeometriskā nozīme punktā
Apsveriet funkcijas y = f(x) grafika sekantu AB tā, lai punktiem A un B būtu attiecīgi koordinātes.

Risinājums
Funkcija ir definēta visiem reālajiem skaitļiem. Tā kā (-1; -3) ir saskares punkts, tad

Nepieciešamie nosacījumi ekstrēmam un pietiekami apstākļi ekstrēmam
Palielinošās funkcijas definīcija. Funkcija y = f(x) palielinās intervālā X, ja tāda ir

Pietiekami kritēriji funkcijas galējībai
Lai atrastu funkcijas maksimumus un minimumus, varat izmantot jebkuru no trim pietiekamajām ekstrēma zīmēm. Lai gan visizplatītākais un ērtākais ir pirmais no tiem.

Noteikta integrāļa pamatīpašības. Īpašība 1. Noteikta integrāļa atvasinājums attiecībā pret augšējo robežu ir vienāds ar integrandu, kurā mainīgā vietā ir integrēts

Ņūtona-Leibnica formula (ar pierādījumu)
Ņūtona-Leibnica formula. Lai funkcija y = f(x) ir nepārtraukta segmentā un F(x) ir viens no funkcijas antiatvasinājumiem šajā segmentā, tad

Dota kāda afīna koordinātu sistēma OXY.

Teorēma 2.1. Jebkurš taisns l koordinātu sistēma OX tiek dota ar formas lineāru vienādojumu

A x+ B y+ C = O, (1)

kur A, B, C R un A 2 + B 2 0. Un otrādi, jebkurš (1) formas vienādojums definē taisni.

Formas (1) vienādojums - taisnas līnijas vispārējais vienādojums .

Pieņemsim, ka vienādojumā (1) visi koeficienti A, B un C nav nulle. Tad

Ah-By=-C un .

Apzīmēsim -C/A=a, -C/B=b. gūt

-līnijas segmenta vienādojums .

Patiešām, skaitļi |a| un |b| norāda ar taisnu līniju nogriezto segmentu izmēru l attiecīgi uz OX un OY asīm.

Ļaujiet līnijai l ir dots ar vispārīgo vienādojumu (1) taisnstūra koordinātu sistēmā un ļaujiet punktiem M 1 (x 1, y 1) un M 2 (x 2, y 2) pieder. l. Tad

A x 1 + B plkst 1 + C = A X 2 + B plkst 2 + C, tas ir, A( x 1 -x 2) + B( plkst 1 -plkst 2) = 0.

Pēdējā vienādība nozīmē, ka vektors \u003d (A, B) ir ortogonāls vektoram \u003d (x 1 -x 2, y 1 -y 2). tie. Tiek izsaukts vektors (A, B). taisnes l normālvektors.

Apsveriet vektoru = (-B, A). Tad

A(-B)+BA=0. tie. ^ .

Tāpēc vektors \u003d (-B, A) ir pikanta virziena vektors l.

Taisnas līnijas parametriskie un kanoniskie vienādojumi

Taisnes līnijas vienādojums, kas iet caur diviem dotiem punktiem

Ļaujiet taisnei norādīt afīnās koordinātu sistēmā (0, X, Y) l, tā virziena vektors = (m,n) un punkts M 0 ( x 0 ,y 0) pieder l. Tad patvaļīgam punktam M ( x,plkst) no šīs rindas mums ir

un kopš tā laika .

Ja mēs iecelsim un

Punktu M un M 0 attiecīgi rādiusa vektori, tad

- taisnas līnijas vienādojums vektora formā.

jo =( X,plkst), =(X 0 ,plkst 0), tad

x= x 0 + mt,

y= y 0 + nt

- taisnas līnijas parametriskais vienādojums .

No tā izriet, ka

- taisnas līnijas kanoniskais vienādojums .

Visbeidzot, ja uz taisnas līnijas l divi punkti M 1 ( X 1 ,plkst 1) un

M2( x 2 ,plkst 2), tad vektors =( X 2 -X 1 ,y 2 -plkst 1) ir vadot taisnās līnijas vektors l. Tad

- vienādojums taisnei, kas iet caur diviem dotiem punktiem.

Divu taisnu līniju savstarpēja izkārtošanās.

Ļaujiet taisni l 1 un l 2 ir doti ar to vispārīgajiem vienādojumiem

l 1: A 1 X+ 1 plkst+ С 1 = 0, (1)

l 2: A 2 X+ B 2 plkst+ C 2 = 0.

Teorēma. Ļaujiet taisni l 1 un l 2 ir doti ar vienādojumu (1). Tad un tikai tad:

1) taisnes krustojas, ja nav tāda skaitļa λ, ka

A1 =λA2, B1 =λB2;

2) taisnes sakrīt, ja ir tāds skaitlis λ, ka

A1 =λA2, B1 =λB2, C1 =λC2;

3) taisnes ir atšķirīgas un paralēlas, ja ir tāds skaitlis λ, ka

A 1 \u003d λA 2, B 1 \u003d λB 2, C 1 λC 2.

taisnu līniju saišķis

Taisnu līniju ķekars ir visu līniju kopums plaknē, kas iet caur kādu punktu centrs staru kūlis.

Lai precizētu staru kūļa vienādojumu, pietiek zināt jebkuras divas taisnes l 1 un l 2, kas iet caur stara centru.

Ļaujiet līnijām afīnās koordinātu sistēmā l 1 un l 2 ir doti ar vienādojumiem

l 1:A1 x+B1 y+ C1 = 0,

l 2:A2 x+ B2 y+ C2 = 0.

Vienādojums:

A 1 x+B1 y+ С + λ (A 2 X+ B 2 y+ C) = 0

- līniju zīmuļa vienādojums, kas definēts ar vienādojumu l 1 un l 2.

Turpmāk ar koordinātu sistēmu mēs saprotam taisnstūra koordinātu sistēmu .

Divu taisnes paralēlisma un perpendikulitātes nosacījumi

Ļaujiet līnijām l 1 un l 2. ar to vispārīgajiem vienādojumiem; = (A 1 ,B 1), = (A 2 ,B 2) ir šo līniju normālie vektori; k 1 = tanα1, k 2 = tgα 2 – slīpuma koeficienti; =( m 1 ,n 1), (m 2 ,n 2) ir virziena vektori. Pēc tam tiešā veidā l 1 un l 2 ir paralēli tad un tikai tad, ja ir patiess viens no šiem nosacījumiem:

vai nu k 1 =k 2 vai .

Lai tagad ir taisni l 1 un l 2 ir perpendikulāri. Tad, protams, , tas ir, A 1 A 2 + B 1 B 2 = 0.

Ja taisni l 1 un l 2 ir attiecīgi doti ar vienādojumiem

l 1: plkst=k 1 x+ b 1 ,

l 2: plkst=k 2 x+ b 2 ,

tad tgα 2 = tg(90º+α) = .

No tā izriet, ka

Visbeidzot, ja un ir līniju virziena vektori, tad ^ , t.i.

m 1 m 2 + n 1 n 2 = 0

Pēdējā attiecība izsaka nepieciešamo un pietiekamo nosacījumu, lai divas plaknes būtu perpendikulāras.

Leņķis starp divām līnijām

Leņķī φ starp divām līnijām l 1 un l 2 mēs sapratīsim mazāko leņķi, caur kuru jāpagriež viena līnija, lai tā kļūtu paralēla citai līnijai vai sakristu ar to, tas ir, 0 £ φ £

Ļaujiet līnijas dot ar vispārīgiem vienādojumiem. Ir skaidrs, ka

cosφ=

Lai tagad ir taisni l 1 un l 2 ir doti vienādojumi ar slīpuma koeficientiem k 1 colla k 2 attiecīgi. Tad

Acīmredzot tas ir ( X-X 0) + B( plkst-plkst 0) + C( z-z 0) = 0

Atvērsim iekavas un apzīmēsim D \u003d -A x 0 - B plkst 0-C z 0 . gūt

A x+ B y+ C z+ D = 0 (*)

- vispārīgais plaknes vienādojums vai vispārīgais plaknes vienādojums.

Teorēma 3.1 Lineārais vienādojums (*) (A 2 +B 2 +C 2 ≠ 0) ir plaknes vienādojums un otrādi, jebkurš plaknes vienādojums ir lineārs.

1) D = 0, tad plakne iet caur sākuma punktu.

2) A \u003d 0, tad plakne ir paralēla OX asij

3) A \u003d 0, B \u003d 0, tad plakne ir paralēla OXY plaknei.

Lai visi vienādojuma koeficienti nav nulle.

- plaknes vienādojums segmentos. Skaitļi |a|, |b|, |c| norāda plaknes nogriezto segmentu izmērus uz koordinātu asīm.

Taisnas līnijas vienādojums segmentos

Ļaujiet dot taisnas līnijas vispārīgo vienādojumu:

Taisnes vienādojums segmentos, kur ir posmi, kurus taisne nogriež uz attiecīgajām koordinātu asīm.

Izveidojiet taisnu līniju, kas norādīta ar vispārējo vienādojumu:

No tā jūs varat izveidot šīs taisnes vienādojumu segmentos:

Taisnu līniju savstarpēja izkārtošanās plaknē.

1. paziņojums.

Līniju secībā un vienādojumos:

Sakritība, nepieciešama un pietiekama, ka:

Pierādījums: un sakrīt, to virziena vektori un ir kolineāri, t.i.:

Ņemsim punktu M 0 ar šīm taisnēm, tad:

Reizinot pirmo vienādojumu ar un pievienojot otrajam, (2) dēļ iegūstam:

Tātad formulas (2), (3) un (4) ir līdzvērtīgas. Turēsimies (2); tad sistēmas (*) vienādojumi ir ekvivalenti; atbilstošās līnijas sakrīt.

2. paziņojums.

Ar vienādojumu (*) dotās taisnes ir paralēlas un nesakrīt tikai tad, ja:

Pierādījums:

Lai tie nesakrīt:

Nekonsekventi, t.i., saskaņā ar Kronecker-Capelli teorēmu:

Tas ir iespējams tikai tad, ja:

Tas ir, saskaņā ar nosacījumu (5).

Kad ir izpildīta pirmā vienādība (5), - otrās vienādības neizpilde rada sistēmas (*) nekonsekvenci, taisnes ir paralēlas un nesakrīt.

1. piezīme.

Polāro koordinātu sistēma.

Nofiksējam punktu lidmašīnā un saucam par stabu. Staru, kas izplūst no pola, sauc par polāro asi.

Mēs izvēlamies skalu segmentu garumu mērīšanai un vienojamies, ka griešanās pretēji pulksteņrādītāja virzienam ap m tiks uzskatīta par pozitīvu. Apsveriet jebkuru punktu dotajā plaknē, apzīmējiet ar tā attālumu līdz polam un sauciet to par polāro rādiusu. Leņķis, par kādu polārā ass jāpagriež, lai tā sakristu ar, tiek apzīmēts ar un tiks saukts par polāro leņķi.

3. definīcija.

Punkta polārās koordinātas ir tā polārais rādiuss un polārais leņķis:

Piezīme 2. pie staba. Punktu vērtība, kas nav punkts, tiek noteikta līdz termiņam.

Apsveriet Dekarta taisnstūra koordinātu sistēmu: pols sakrīt ar sākumu, un polārā ass sakrīt ar pozitīvo pusasi. Šeit. Pēc tam:

Kāda ir saistība starp taisnstūra Dekarta un polāro koordinātu sistēmām.

Bernulli lemniskāta vienādojums. Pierakstiet to polārajās koordinātēs.

Normāls taisnes vienādojums plaknē. Ļaujiet polārajai asij sakrist ar, - asi, kas iet caur izcelsmi. Ļaujiet:

Ļaujiet tad:

Nosacījums (**) punktam:

Taisnes vienādojums polāro koordinātu sistēmā.

Šeit - garums, kas novilkts no sākuma līdz taisnei, - normālā slīpuma leņķis pret asi.

Vienādojumu (7) var pārrakstīt:

Normāls taisnes vienādojums plaknē.

Taisnes līnijas īpašības Eiklīda ģeometrijā.

Ir bezgala daudz līniju, kuras var novilkt caur jebkuru punktu.

Caur jebkuriem diviem punktiem, kas nesakrīt, ir tikai viena taisne.

Divas nesakrītošas ​​līnijas plaknē vai nu krustojas vienā punktā, vai arī ir

paralēli (seko no iepriekšējās).

Trīsdimensiju telpā divu līniju relatīvajam novietojumam ir trīs iespējas:

• līnijas krustojas;

• taisnas līnijas ir paralēlas;

• taisnas līnijas krustojas.

Taisni līnija- pirmās kārtas algebriskā līkne: Dekarta koordinātu sistēmā taisne

plaknē ir dots ar pirmās pakāpes vienādojumu (lineārais vienādojums).

Vispārīgais taisnes vienādojums.

Definīcija. Jebkuru plaknes līniju var norādīt ar pirmās kārtas vienādojumu

Ah + Wu + C = 0,

un nemainīgs A, B tajā pašā laikā nav vienāds ar nulli. Šo pirmās kārtas vienādojumu sauc ģenerālis

taisnās līnijas vienādojums. Atkarībā no konstantu vērtībām A, B un AR Ir iespējami šādi īpaši gadījumi:

. C = 0, A ≠ 0, B ≠ 0- līnija iet caur izcelsmi

. A = 0, B ≠0, C ≠0 (pēc + C = 0)- taisna līnija, kas ir paralēla asij Ak

. B = 0, A ≠ 0, C ≠ 0 (Ax + C = 0)- taisna līnija, kas ir paralēla asij OU

. B = C = 0, A ≠ 0- līnija sakrīt ar asi OU

. A = C = 0, B ≠ 0- līnija sakrīt ar asi Ak

Taisnas līnijas vienādojumu var attēlot dažādās formās atkarībā no dotā

sākotnējie nosacījumi.

Taisnes vienādojums ar punktu un normālu vektoru.

Definīcija. Dekarta taisnstūra koordinātu sistēmā vektors ar komponentiem (A, B)

perpendikulāri taisnei, kas dota vienādojumā

Ah + Wu + C = 0.

Piemērs. Atrodiet vienādojumu taisnei, kas iet caur punktu A(1, 2) perpendikulāri vektoram (3, -1).

Risinājums. Sastādām pie A \u003d 3 un B \u003d -1 taisnes vienādojumu: 3x - y + C \u003d 0. Lai atrastu koeficientu C

iegūtajā izteiksmē aizvietojam dotā punkta A koordinātes. Iegūstam: 3 - 2 + C = 0, tāpēc

C = -1. Kopā: vēlamais vienādojums: 3x - y - 1 \u003d 0.

Taisnes līnijas vienādojums, kas iet caur diviem punktiem.

Telpā ir doti divi punkti M 1 (x 1 , y 1 , z 1) un M2 (x 2, y 2, z 2), tad taisnās līnijas vienādojums,

iet caur šiem punktiem:

Ja kāds no saucējiem ir vienāds ar nulli, atbilstošais skaitītājs ir jāiestata vienāds ar nulli. Uz

plaknē, iepriekš uzrakstītais taisnes vienādojums ir vienkāršots:

ja x 1 ≠ x 2 un x = x 1, ja x 1 = x 2 .

Frakcija = k sauca slīpuma koeficients taisni.

Piemērs. Atrodiet vienādojumu taisnei, kas iet caur punktiem A(1, 2) un B(3, 4).

Risinājums. Izmantojot iepriekš minēto formulu, mēs iegūstam:

Taisnes vienādojums ar punktu un slīpumu.

Ja taisnes vispārīgais vienādojums Ah + Wu + C = 0 izveido formu:

un iecelt , tad tiek izsaukts iegūtais vienādojums

taisnas līnijas ar slīpumu k vienādojums.

Punkta taisnes un virziena vektora vienādojums.

Pēc analoģijas ar punktu, kurā tiek ņemts vērā taisnes vienādojums caur normālu vektoru, varat ievadīt uzdevumu

taisne caur punktu un taisnes virziena vektors.

Definīcija. Katrs vektors, kas nav nulle (α 1 , α 2), kuras sastāvdaļas atbilst nosacījumam

Aα 1 + Bα 2 = 0 sauca taisnes virziena vektors.

Ah + Wu + C = 0.

Piemērs. Atrodiet vienādojumu taisnei ar virziena vektoru (1, -1) un iet caur punktu A(1, 2).

Risinājums. Mēs meklēsim vajadzīgās taisnes vienādojumu formā: Ax + By + C = 0. Saskaņā ar definīciju,

koeficientiem jāatbilst šādiem nosacījumiem:

1 * A + (-1) * B = 0, t.i. A = B.

Tad taisnas līnijas vienādojumam ir šāda forma: Ax + Ay + C = 0, vai x + y + C / A = 0.

plkst x=1, y=2 mēs saņemam C/ A = -3, t.i. vēlamais vienādojums:

x + y - 3 = 0

Taisnas līnijas vienādojums segmentos.

Ja taisnes vispārējā vienādojumā Ah + Wu + C = 0 C≠0, tad, dalot ar -C, iegūstam:

vai, kur

Koeficientu ģeometriskā nozīme ir tāda, ka koeficients a ir krustošanās punkta koordināte

taisni ar asi Ak, a b- taisnes krustošanās punkta koordinātas ar asi OU.

Piemērs. Ir dots taisnes vispārīgais vienādojums x - y + 1 = 0. Atrodiet šīs taisnes vienādojumu segmentos.

C = 1, a \u003d -1, b = 1.

Normāls taisnes vienādojums.

Ja vienādojuma abas puses Ah + Wu + C = 0 dalīt ar skaitli , ko sauc

normalizējošais faktors, tad mēs saņemam

xcosφ + ysinφ - p = 0 -taisnas līnijas normāls vienādojums.

Normalizējošā koeficienta zīme ± jāizvēlas tā, lai μ * C< 0.

R- perpendikula garums, kas samazināts no sākuma līdz līnijai,

a φ - leņķis, ko veido šis perpendikuls ar ass pozitīvo virzienu Ak.

Piemērs. Dots taisnes vispārīgais vienādojums 12x - 5g - 65 = 0. Nepieciešams, lai uzrakstītu dažāda veida vienādojumus

šī taisnā līnija.

Šīs taisnes vienādojums segmentos:

Šīs līnijas vienādojums ar slīpumu: (dalīt ar 5)

Taisnas līnijas vienādojums:

cos φ = 12/13; sin φ= -5/13; p=5.

Jāņem vērā, ka ne katru taisni var attēlot ar vienādojumu segmentos, piemēram, taisnes,

paralēli asīm vai iet caur izcelsmi.

Leņķis starp līnijām plaknē.

Definīcija. Ja ir dotas divas rindas y \u003d k 1 x + b 1, y \u003d k 2 x + b 2, tad akūts leņķis starp šīm līnijām

tiks definēts kā

Divas taisnes ir paralēlas, ja k 1 = k 2. Divas līnijas ir perpendikulāras

ja k 1 \u003d -1 / k 2 .

Teorēma.

Tieša Ah + Wu + C = 0 un A 1 x + B 1 y + C 1 \u003d 0 ir paralēli, ja koeficienti ir proporcionāli

A 1 \u003d λA, B 1 \u003d λB. Ja arī С 1 \u003d λС, tad līnijas sakrīt. Divu taisnes krustošanās punkta koordinātas

tiek atrasti kā risinājums šo līniju vienādojumu sistēmai.

Taisnes vienādojums, kas iet caur noteiktu punktu, ir perpendikulārs noteiktai taisnei.

Definīcija. Līnija, kas iet caur punktu M 1 (x 1, y 1) un perpendikulāri līnijai y = kx + b

attēlots ar vienādojumu:

Attālums no punkta līdz līnijai.

Teorēma. Ja tiek dots punkts M(x 0, y 0), tad attālums līdz līnijai Ah + Wu + C = 0 definēts kā:

Pierādījums. Ļaujiet punktu M 1 (x 1, y 1)- perpendikula pamatne nokrita no punkta M par doto

tiešā veidā. Tad attālums starp punktiem M un M 1:

(1)

Koordinātas x 1 un 1 var atrast kā vienādojumu sistēmas risinājumu:

Sistēmas otrais vienādojums ir taisnes vienādojums, kas iet caur doto punktu M 0 perpendikulāri

dotā līnija. Ja mēs pārveidosim pirmo sistēmas vienādojumu formā:

A(x - x 0) + B(y - y 0) + Ax 0 + Ar 0 + C = 0,

tad, atrisinot, mēs iegūstam:

Aizvietojot šīs izteiksmes vienādojumā (1), mēs atrodam:

Teorēma ir pierādīta.