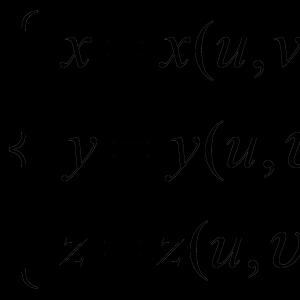Pieskares plakne un virsma normāla. Virsmas pieskares plakne normālai un virsmai pieskares plakne

Lejupielādēt no vietnes Depositfiles

4. VIRSMU TEORIJA.

4.1. VIRSMU VIENĀDĀJUMI.

Virsmu 3D telpā var definēt:

1) netieši: F ( x , y , z ) =0 (4.1)

2) skaidri: z = f ( x , y ) (4.2)

3) parametriski: (4.3)

vai:
(4.3’)

kur ir skalārie argumenti
dažreiz sauc par līknes koordinātām. Piemēram, sfēra
ir ērti iestatīt sfēriskās koordinātās:
.

4.2. TANGENTES LAKNE UN NORMĀLA VIRSMAI.

Ja taisne atrodas uz virsmas (4.1), tad tās punktu koordinātas atbilst virsmas vienādojumam:

Atšķirot šo identitāti, mēs iegūstam:

(4.4)

vai
(4.4 ’ )

katrā virsmas līknes punktā. Tādējādi gradienta vektors virsmas nevienskaitļa punktos (kuros funkcija (4.5) ir diferencējama un
) ir perpendikulāra jebkuras virsmas līnijas pieskares vektoriem, t.i., var izmantot kā normālu vektoru, lai formulētu pieskares plaknes vienādojumu punktā M 0 (x 0 , y 0 , z 0 ) virsmas

(4.6)

un kā virziena vektors parastajā vienādojumā:

(4.7)

Virsmas eksplicīta (4.2) piešķiršanas gadījumā pieskares plaknes un normas vienādojumi ir attiecīgi šādi:

(4.8)

un
(4.9)

Virsmas parametriskajā attēlojumā (4.3.) vektori
atrodas pieskares plaknē, un pieskares plaknes vienādojumu var uzrakstīt šādi:

(4.10)

un to vektora reizinājumu var uzskatīt par virzošo normālo vektoru:

un parasto vienādojumu var uzrakstīt šādi:

(4.11)

kur
- parametru vērtības, kas atbilst punktam M 0 .

Tālāk mēs aprobežojamies ar to virsmas punktu ņemšanu vērā, kur atrodas vektori

nav vienādi ar nulli un nav paralēli.

Piemērs 4.1 Sastādiet pieskares plaknes un normālās vienādojumus punktā M 0 (1,1,2) uz apgriezienu paraboloīda virsmu
.

Risinājums: tā kā paraboloīda vienādojums ir dots skaidri, saskaņā ar (4.8) un (4.9) mums ir jāatrod
punktā M 0 :

, un punktā M 0
. Tad pieskares plaknes vienādojums punktā M 0 būs šādā formā:

2(x -1)+2(y -1)-(z-2)=0 vai 2 x +2 y -z - 2=0, un parastais vienādojums
.

Piemērs 4.2 Sastādiet pieskares plaknes un normālās vienādojumus patvaļīgā helikoīda punktā
, .

Risinājums. Šeit ,

Pieskares plaknes vienādojums:

vai

Parastie vienādojumi:

.

4.3. VIRSMAS PIRMĀ KVADRĀTiskā FORMA.

Ja virsma ir dota ar vienādojumu

tad līkne
uz to var dot ar vienādojumu
(4.12)

Rādiusa vektora diferenciālis
pa līkni, kas atbilst nobīdei no punkta M 0 uz tuvējo punktu M, ir vienāds ar

(4.13)

Jo
ir līknes loka diferenciālis, kas atbilst vienam un tam pašam pārvietojumam), tad

(4.14)

kur .

Izteiksme (4.14) labajā pusē tiek saukta par virsmas pirmo kvadrātisko formu, un tai ir milzīga loma virsmu teorijā.

Integrējošais diferenciālisds sākot no t 0 (atbilst punktam M 0 ) līdz t (atbilst punktam M), iegūstam atbilstošā līknes segmenta garumu

(4.15)

Zinot pirmo virsmas kvadrātisko formu, var atrast ne tikai garumus, bet arī leņķus starp līknēm.

Ja du , dv ir līknes koordinātu diferenciāles, kas atbilst bezgalīgi mazai nobīdei vienā līknē, un
— no otras puses, ņemot vērā (4.13.):

(4.16)

Izmantojot formulu

(4.17)

pirmā kvadrātiskā forma ļauj aprēķināt reģiona laukumu
virsmas.

Piemērs 4.3 Uz helikoīda atrodiet spirāles garumu
starp diviem punktiem.

Risinājums. Jo uz spirāles
, tad. Atrodi punktā
pirmā kvadrātiskā forma. Apzīmējot unv = t , mēs iegūstam šīs spirāles vienādojumu formā . Kvadrātiskā forma:

= - pirmā kvadrātiskā forma.

Šeit . Formulā (4.15) šajā gadījumā
un loka garums:

=

4.4. VIRSMAS OTRĀ KVADRĀTISKĀ FORMA.

Apzīmē
- vienība normāls vektors pret virsmu
:

(4.18) . (4.23)

Virsmas līniju sauc par izliekuma līniju, ja tās virziens katrā punktā ir galvenais virziens.

4.6. VIRSMAS ĢEOĒZISKO LĪNIJU JĒDZIENS.

Definīcija 4.1 . Virsmas līkni sauc par ģeodēzisku, ja tā ir galvenā norma katrā punktā, kur izliekums nav nulle, sakrīt ar normālu uz virsmu.

Caur katru virsmas punktu jebkurā virzienā iet, un tikai viens ģeodēzisks. Piemēram, uz sfēras lielie apļi ir ģeodēzija.

Virsmas parametrizāciju sauc par daļēji ģeodēzisku, ja viena koordinātu līniju saime sastāv no ģeodēzijas, bet otra ir tai ortogonāla. Piemēram, uz sfēras meridiāniem (ģeodēziem) un paralēlēm.

Ģeodēzija uz pietiekami maza segmenta ir īsākā no visām līknēm, kas ir tuvu tam, kas savieno vienus un tos pašus punktus.

Kādā brīdī un tai ir nepārtraukti parciālie atvasinājumi, no kuriem vismaz viens nepazūd, tad šī punkta tuvumā būs vienādojuma (1) dotā virsma pareiza virsma.

Papildus iepriekšminētajam netiešs iestatīšanas veids virsmu var definēt skaidri, ja vienu no mainīgajiem, piemēram, z, var izteikt ar citiem:

Arī pastāv parametrisks piešķiršanas metode. Šajā gadījumā virsmu nosaka vienādojumu sistēma:

Vienkāršas virsmas jēdziens

Precīzāk, gluda virsma ir vienības kvadrāta interjera homeomorfās kartēšanas (tas ir, viens pret vienu un savstarpēji nepārtrauktas kartēšanas) attēls. Šai definīcijai var dot analītisku izteiksmi.

Dots kvadrāts uz plaknes ar taisnstūra koordinātu sistēmu u un v , kuras iekšējo punktu koordinātes apmierina nevienādības 0< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

Piemērs vienkārša virsma ir puslode. Visa teritorija nav gluda virsma. Tas rada nepieciešamību turpmāk vispārināt virsmas jēdzienu.

Telpas apakškopa, kurā katram punktam ir apkārtne, kas ir gluda virsma, tiek saukts pareiza virsma .

Virsma diferenciālajā ģeometrijā

Helikoīds

katenoīds

Metrika viennozīmīgi nenosaka virsmas formu. Piemēram, helikoīda un katenoīda metrika, kas parametrizēta atbilstošā veidā, sakrīt, tas ir, starp to reģioniem pastāv atbilstība, kas saglabā visus garumus (izometrija). Tiek sauktas īpašības, kas tiek saglabātas izometrisko transformāciju rezultātā iekšējā ģeometrija virsmas. Iekšējā ģeometrija nav atkarīga no virsmas stāvokļa telpā un nemainās, kad tā ir saliekta bez spriedzes un saspiešanas (piemēram, kad cilindrs ir saliekts konusā).

Metriskie koeficienti nosaka ne tikai visu līkņu garumus, bet kopumā visu virsmas iekšienē veikto mērījumu rezultātus (leņķi, laukumi, izliekums utt.). Tāpēc viss, kas ir atkarīgs tikai no metrikas, attiecas uz iekšējo ģeometriju.

Normāla un normāla sadaļa

Normālie vektori virsmas punktos

Viena no galvenajām virsmas īpašībām ir tā normāli- vienības vektors, kas ir perpendikulārs pieskares plaknei noteiktā punktā:

.

Normāla zīme ir atkarīga no koordinātu izvēles.

Virsmas griezums pa plakni, kas satur normālu (noteiktā punktā), veido noteiktu līkni uz virsmas, ko sauc parastā sadaļa virsmas. Galvenais normāls normālai sadaļai sakrīt ar normālu pret virsmu (līdz zīmei).

Ja līkne uz virsmas nav normāls griezums, tad tās galvenais normāls veido leņķi θ ar virsmas normālu. Tad izliekums k līkne ir saistīta ar izliekumu k n parastā sadaļa (ar tādu pašu pieskares) Meunier formula:

Normālā vektora koordinātas dažādiem virsmas noteikšanas veidiem ir norādītas tabulā:

	Normālas koordinātas virsmas punktā
netiešs uzdevums
skaidrs uzdevums
parametrisks uzdevums

Izliekums

Dažādiem virzieniem noteiktā virsmas punktā tiek iegūts atšķirīgs normālā griezuma izliekums, ko sauc normāls izliekums; tai piešķir plusa zīmi, ja līknes galvenais normāls iet tajā pašā virzienā kā normāls uz virsmu, vai mīnusa zīmi, ja normālu virzieni ir pretēji.

Vispārīgi runājot, katrā virsmas punktā ir divi perpendikulāri virzieni e 1 un e 2 , kurā normālajam izliekumam ir minimālās un maksimālās vērtības; šos virzienus sauc galvenais. Izņēmums ir gadījums, kad normālais izliekums ir vienāds visos virzienos (piemēram, sfēras tuvumā vai apgriezienu elipsoīda beigās), tad visi virzieni punktā ir galvenie.

Virsmas ar negatīvu (pa kreisi), nulli (centru) un pozitīvu (labo) izliekumu.

Tiek saukti normāli izliekumi galvenajos virzienos galvenie izliekumi; apzīmēsim tos ar κ 1 un κ 2 . Izmērs:

K= κ 1 κ 2

sauca Gausa izliekums, pilns izliekums vai vienkārši izliekums virsmas. Ir arī termins izliekuma skalārs, kas nozīmē izliekuma tenzora konvolūcijas rezultātu; šajā gadījumā izliekuma skalārs ir divreiz lielāks par Gausa izliekumu.

Gausa izliekumu var aprēķināt, izmantojot metriku, un tāpēc tas ir virsmu iekšējās ģeometrijas objekts (ņemiet vērā, ka galvenie izliekumi neattiecas uz iekšējo ģeometriju). Pēc izliekuma zīmes jūs varat klasificēt virsmas punktus (sk. attēlu). Plaknes izliekums ir nulle. Sfēras ar rādiusu R izliekums visur ir vienāds ar . Ir arī nemainīga negatīva izliekuma virsma - pseidosfēra.

Ģeodēziskās līnijas, ģeodēziskais izliekums

Virsmas līkni sauc ģeodēziskā līnija vai vienkārši ģeodēziskais, ja visos tā punktos līknes galvenais normāls sakrīt ar virsmas normālu. Piemērs: plaknē ģeodēzija būs taisnas līnijas un līniju segmenti, uz sfēras - lielie apļi un to segmenti.

Ekvivalenta definīcija: ģeodēziskajai līnijai tās galvenās normas projekcija uz blakus plakni ir nulles vektors. Ja līkne nav ģeodēziska, tad norādītā projekcija nav nulle; tā garumu sauc ģeodēziskais izliekums k g izliekums uz virsmas. Ir attiecība:

,

kur k ir šīs līknes izliekums, k n- tās parastās sekcijas izliekums ar tādu pašu pieskari.

Ģeodēziskās līnijas attiecas uz iekšējo ģeometriju. Mēs uzskaitām to galvenās īpašības.

• Viena un tikai viena ģeodēzija iet caur noteiktu virsmas punktu noteiktā virzienā.
• Pietiekami mazā virsmas laukumā divus punktus vienmēr var savienot ar ģeodēzisko ierīci, turklāt tikai vienu. Paskaidrojums: uz sfēras pretējos polius savieno bezgalīgs meridiānu skaits, un divus tuvus punktus var savienot ne tikai ar liela apļa segmentu, bet arī ar to pievienošanu pilnam aplim, tā ka unikalitāte tiek novērota tikai mazā.
• Ģeodēziskais ir īsākais. Stingrāk: uz neliela virsmas gabala īsākais ceļš starp dotajiem punktiem atrodas gar ģeodēzisko līniju.

Kvadrāts

Vēl viens svarīgs virsmas atribūts ir tā kvadrāts, ko aprēķina pēc formulas:

Virsma ir definēta kā punktu kopa, kuras koordinātas atbilst noteikta veida vienādojumam:

F (x , y , z) = 0 (1) (\displaystyle F(x,\,y,\,z)=0\qquad (1))

Ja funkcija F (x , y , z) (\displaystyle F(x,\,y,\,z)) ir nepārtraukts kādā punktā un tajā ir nepārtraukti parciālie atvasinājumi, no kuriem vismaz viens nepazūd, tad šī punkta tuvumā būs vienādojuma (1) dotā virsma pareiza virsma.

Papildus iepriekšminētajam netiešs iestatīšanas veids, virsmu var definēt skaidri, ja vienu no mainīgajiem, piemēram, z, var izteikt ar pārējiem:

z = f (x, y) (1 ′) (\displaystyle z=f(x,y)\qquad (1"))

Stingrāk, gluda virsma ir vienības kvadrāta interjera homeomorfās kartēšanas (tas ir, viens pret vienu un savstarpēji nepārtrauktas kartēšanas) attēls. Šai definīcijai var dot analītisku izteiksmi.

Dots kvadrāts uz plaknes ar taisnstūra koordinātu sistēmu u un v , kuras iekšējo punktu koordinātes apmierina nevienādības 0< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

Piemērs vienkārša virsma ir puslode. Visa teritorija nav gluda virsma. Tas rada nepieciešamību turpmāk vispārināt virsmas jēdzienu.

Telpas apakškopa, kurā katram punktam ir apkārtne, kas ir gluda virsma, tiek saukts pareiza virsma .

Virsma diferenciālajā ģeometrijā

Helikoīds

katenoīds

Metrika viennozīmīgi nenosaka virsmas formu. Piemēram, helikoīda un katenoīda metrika, kas parametrizēta atbilstošā veidā, sakrīt, tas ir, starp to reģioniem pastāv atbilstība, kas saglabā visus garumus (izometrija). Tiek sauktas īpašības, kas tiek saglabātas izometrisko transformāciju rezultātā iekšējā ģeometrija virsmas. Iekšējā ģeometrija nav atkarīga no virsmas stāvokļa telpā un nemainās, kad tā ir saliekta bez spriedzes un saspiešanas (piemēram, kad cilindrs ir saliekts konusā).

Metriskie koeficienti E , F , G (\displaystyle E,\ F,\ G) noteikt ne tikai visu līkņu garumus, bet kopumā visu virsmas iekšienē veikto mērījumu rezultātus (leņķi, laukumi, izliekums utt.). Tāpēc viss, kas ir atkarīgs tikai no metrikas, attiecas uz iekšējo ģeometriju.

Normāla un normāla sadaļa

Normālie vektori virsmas punktos

Viena no galvenajām virsmas īpašībām ir tā normāli- vienības vektors, kas ir perpendikulārs pieskares plaknei noteiktā punktā:

m = [ r u ′ , r v ′ ] | [ r u ′ , r v ′ ] | (\displaystyle \mathbf (m) =(\frac ([\mathbf (r"_(u)) ,\mathbf (r"_(v)) ])(|[\mathbf (r"_(u)) ,\mathbf (r"_(v)) ]|))).

Normāla zīme ir atkarīga no koordinātu izvēles.

Virsmas griezums pa plakni, kas satur virsmas normālu noteiktā punktā, veido noteiktu līkni, ko sauc parastā sadaļa virsmas. Galvenais normāls normālai sadaļai sakrīt ar normālu pret virsmu (līdz zīmei).

Ja līkne uz virsmas nav normāls griezums, tad tās galvenais normāls veido leņķi ar virsmas normālu θ (\displaystyle \theta ). Tad izliekums k (\displaystyle k) līkne ir saistīta ar izliekumu k n (\displaystyle k_(n)) parastā sadaļa (ar tādu pašu pieskares) Meunier formula:

k n = ± k cos θ (\displaystyle k_(n)=\pm k\,\cos \,\theta)

Normālā vektora koordinātas dažādiem virsmas noteikšanas veidiem ir norādītas tabulā:

	Normālas koordinātas virsmas punktā
netiešs uzdevums	(∂ F ∂ x ; ∂ F ∂ y ; ∂ F ∂ z) (∂ F ∂ x) 2 + (∂ F ∂ y) 2 + (∂ F ∂ z) 2 (\displaystyle (\frac (\left(()) \frac (\partial F)(\partial x));\,(\frac (\partial F)(\partial y));\,(\frac (\partial F)(\partial z))\right) )(\sqrt (\left((\frac (\partial F)(\partial x))\right)^(2)+\left((\frac (\partial F)(\partial y))\right) ^(2)+\left((\frac (\partial F)(\partial z))\right)^(2)))))
skaidrs uzdevums	(− ∂ f ∂ x ; − ∂ f ∂ y ; 1) (∂ f ∂ x) 2 + (∂ f ∂ y) 2 + 1 (\displaystyle (\frac (\left(-(\frac (\partial f)) )(\partial x));\,-(\frac (\partial f)(\partial y));\,1\right))(\sqrt (\left((\frac (\partial f)(\)) daļēja x))\labais)^(2)+\kreisais((\frac (\partial f)(\partial y))\right)^(2)+1))))
parametrisks uzdevums	(D (y , z) D (u , v) ; D (z , x) D (u , v) ; D (x , y) D (u , v)) (D (y , z) D (u , v)) 2 + (D (z , x) D (u , v)) 2 + (D (x, y) D (u , v)) 2 (\displaystyle (\frac (\left() (D(y,z))(D(u,v)));\,(\frac (D(z,x))(D(u,v)));\,(\frac (D(x) ,y))(D(u,v)))\right))(\sqrt (\left((\frac (D(y,z)))(D(u,v)))\right)^(2 )+\left((\frac (D(z,x))(D(u,v)))\right)^(2)+\left((\frac (D(x,y))(D( u,v)))\pa labi)^(2))))

Šeit D (y , z) D (u , v) = | y u ′ y v ′ z u ′ z v ′ | , D (z , x) D (u , v) = | z u ′ z v ′ x u ′ x v ′ | , D (x, y) D (u, v) = | x u ′ x v ′ y u ′ y v ′ | (\displaystyle (\frac (D(y,z))(D(u,v)))=(\begin(vmatrix)y"_(u)&y"_(v)\\z"_(u) &z"_(v)\end(vmatrix)),\quad (\frac (D(z,x))(D(u,v)))=(\begin(vmatrix)z"_(u)&z" _(v)\\x"_(u)&x"_(v)\end(vmatrix)),\quad (\frac (D(x,y))(D(u,v)))=(\ sākums(vmatrica)x"_(u)&x"_(v)\\y"_(u)&y"_(v)\end(vmatrix))).

Visi atvasinājumi tiek ņemti punktā (x 0, y 0, z 0) (\displeja stils (x_(0),y_(0),z_(0))).

Izliekums

Dažādiem virzieniem noteiktā virsmas punktā tiek iegūts atšķirīgs normālā griezuma izliekums, ko sauc normāls izliekums; tai piešķir plusa zīmi, ja līknes galvenais normāls iet tajā pašā virzienā kā normāls uz virsmu, vai mīnusa zīmi, ja normālu virzieni ir pretēji.

Vispārīgi runājot, katrā virsmas punktā ir divi perpendikulāri virzieni e 1 (\displaystyle e_(1)) un e 2 (\displaystyle e_(2)), kurā parastajam izliekumam ir minimālās un maksimālās vērtības; šos virzienus sauc galvenais. Izņēmums ir gadījums, kad normālais izliekums ir vienāds visos virzienos (piemēram, sfēras tuvumā vai apgriezienu elipsoīda beigās), tad visi virzieni punktā ir galvenie.

Virsmas ar negatīvu (pa kreisi), nulli (centru) un pozitīvu (labo) izliekumu.

Tiek saukti normāli izliekumi galvenajos virzienos galvenie izliekumi; apzīmēsim tos κ 1 (\displaystyle \kappa _(1)) un κ 2 (\displaystyle \kappa _(2)). Izmērs:

K = κ 1 κ 2 (\displaystyle K=\kappa _(1)\kappa _(2))

2 mainīgo z = f(x,y) funkcijas grafiks ir virsma, kas projicēta uz XOY plaknes funkcijas D jomā.
Apsveriet virsmu σ , kas dots ar vienādojumu z = f(x,y) , kur f(x,y) ir diferencējama funkcija, un lai M 0 (x 0 ,y 0 ,z 0) ir fiksēts punkts uz virsmas σ , t.i. z0 = f(x0,y0). Pieraksts. Tiešsaistes kalkulators ir paredzēts, lai atrastu pieskares plaknes un virsmas normālvienādojumi. Lēmums tiek pieņemts Word formātā. Ja jums ir jāatrod līknes pieskares vienādojums (y = f(x)), tad jums ir jāizmanto šis pakalpojums.

Funkciju ievadīšanas noteikumi:

Funkciju ievadīšanas noteikumi:

1. Visi mainīgie ir izteikti kā x,y,z

Pieskares plakne pret virsmu σ viņas punktā M 0 ir plakne, kurā atrodas visu uz virsmas uzzīmēto līkņu pieskares σ caur punktu M 0 .
Virsmas pieskares plaknes vienādojumam, kas dots ar vienādojumu z = f(x,y) punktā M 0 (x 0 ,y 0 ,z 0), ir šāda forma:

z - z 0 \u003d f 'x (x 0, y 0) (x - x 0) + f ' y (x 0, y 0) (y - y 0)

Vektoru sauc par virsmas normālo vektoru σ punktā M 0 . Normāls vektors ir perpendikulārs pieskares plaknei.
Normāls pret virsmu σ punktā M 0 ir taisna līnija, kas iet caur šo punktu un kurai ir vektora N virziens.
Virsmas normāldaļas kanoniskie vienādojumi, kas doti ar vienādojumu z = f(x,y) punktā M 0 (x 0 ,y 0 ,z 0), kur z 0 = f(x 0 ,y 0), ir šāda forma:

1. piemērs. Virsma tiek dota ar vienādojumu x 3 +5y . Atrast virsmas pieskares plaknes vienādojumu punktā M 0 (0;1).
Risinājums. Pieskares vienādojumus rakstīsim vispārīgā formā: z - z 0 \u003d f "x (x 0, y 0, z 0) (x - x 0) + f" y (x 0, y 0, z 0) (y - y 0)
Pēc uzdevuma nosacījuma x 0 = 0, y 0 = 1, tad z 0 = 5
Atrodiet funkcijas z = x^3+5*y daļējos atvasinājumus:
f" x (x, y) = (x 3 + 5 y)" x = 3 x 2
f" x (x, y) = (x 3 + 5 y)" y = 5
Punktā M 0 (0,1) daļējo atvasinājumu vērtības:
f"x(0;1) = 0
f"y (0; 1) = 5
Izmantojot formulu, mēs iegūstam virsmas pieskares plaknes vienādojumu punktā M 0: z - 5 \u003d 0 (x - 0) + 5 (y - 1) vai -5 y + z \u003d 0

2. piemērs. Virsma ir norādīta netieši y 2 -1/2*x 3 -8z. Atrast virsmas pieskares plaknes vienādojumu punktā M 0 (1;0;1).
Risinājums. Mēs atrodam funkcijas daļējus atvasinājumus. Tā kā funkcija ir norādīta netiešā veidā, mēs meklējam atvasinājumus pēc formulas:

Mūsu funkcijai:

Pēc tam:

Punktā M 0 (1,0,1) daļēju atvasinājumu vērtības:
f "x (1; 0; 1) \u003d -3/16
f"y(1;0;1) = 0
Izmantojot formulu, mēs iegūstam virsmas pieskares plaknes vienādojumu punktā M 0: z - 1 \u003d -3 / 16 (x - 1) + 0 (y - 0) vai 3 / 16 x + z- 19 / 16 \u003d 0

Piemērs. Virsma σ ko dod vienādojums z= y/x + xy – 5x 3 . Atrodiet virsmas pieskares plaknes un normālās vienādojumu σ punktā M 0 (x 0 ,y 0 ,z 0) piederība tai, ja x 0 = –1, y 0 = 2.
Atradīsim funkcijas daļējos atvasinājumus z= f(x,y) = y/x + xy – 5x 3:
f x '( x,y) = (y/x + xy – 5x 3)' x \u003d - y / x 2 + y – 15x 2 ;
f y' ( x,y) = (y/x + xy – 5x 3)' y = 1/x + x.
Punkts M 0 (x 0 ,y 0 ,z 0) pieder virsmai σ , lai mēs varētu aprēķināt z 0 , aizstājot doto x 0 = -1 un y 0 = 2 virsmas vienādojumā:

z= y/x + xy – 5x 3

z 0 = 2/(-1) + (–1) 2 – 5 (–1) 3 = 1.
Punktā M 0 (–1, 2, 1) daļēju atvasinājumu vērtības:
f x '( M 0) = –1/(-1) 2 + 2 – 15(–1) 2 = –15; fy'( M 0) = 1/(-1) – 1 = –2.
Izmantojot formulu (5), iegūstam virsmas pieskares plaknes vienādojumu σ punktā M 0:
z – 1= –15(x + 1) – 2(y – 2) z – 1= –15x – 15 – 2y + 4 15x + 2y + z + 10 = 0.
Izmantojot formulu (6), iegūstam virsmas normālā kanoniskos vienādojumus σ punktā M 0: .
Atbildes: pieskares plaknes vienādojums: 15 x + 2y + z+ 10 = 0; normālie vienādojumi: .

1. piemērs. Dota funkcija z \u003d f (x, y) un divi punkti A (x 0, y 0) un B (x 1, y 1). Nepieciešams: 1) aprēķina funkcijas vērtību z 1 punktā B; 2) aprēķina funkcijas aptuveno vērtību z 1 punktā B, pamatojoties uz funkcijas vērtību z 0 punktā A, aizstājot funkcijas pieaugumu pārejas laikā no punkta A uz punktu B ar diferenciāli; 3) sastāda virsmas z = f(x,y) pieskares plaknes vienādojumu punktā C(x 0 ,y 0 ,z 0).
Risinājums.
Mēs rakstām pieskares vienādojumus vispārīgā formā:
z - z 0 \u003d f "x (x 0, y 0, z 0) (x - x 0) + f" y (x 0, y 0, z 0) (y - y 0)
Atbilstoši uzdevuma nosacījumam x 0 = 1, y 0 = 2, tad z 0 = 25
Atrodiet funkcijas z = f(x,y)x^2+3*x*y*+y^2 daļējos atvasinājumus:
f "x (x, y) \u003d (x 2 +3 x y + y 2)" x \u003d 2 x + 3 y 3
f "x (x, y) \u003d (x 2 +3 x y + y 2)" y \u003d 9 x y 2
Punktā M 0 (1.2) daļējo atvasinājumu vērtības:
f" x (1; 2) = 26
f"y (1; 2) = 36
Izmantojot formulu, iegūstam virsmas pieskares plaknes vienādojumu punktā M 0:
z - 25 = 26 (x - 1) + 36 (y - 2)
vai
-26x-36y+z+73 = 0

2. piemērs. Uzrakstiet elipsveida paraboloīda z = 2x 2 + y 2 pieskares plaknes un normāles vienādojumus punktā (1;-1;3).

Definīcija. Punktu, kas atrodas uz otrās kārtas virsmas, ko nosaka vispārīgais vienādojums (1) attiecībā pret ODSC, sauc par nevienskaitli, ja starp trim skaitļiem: ir vismaz viens, kas nav vienāds ar nulli.

Tādējādi punkts, kas atrodas uz otrās kārtas virsmas, nav vienskaitlis tad un tikai tad, ja tas ir tā centrs, pretējā gadījumā, ja virsma ir koniska un punkts ir šīs virsmas virsotne.

Definīcija. Otrās kārtas virsmas pieskare noteiktā nevienskaitlī punktā ir taisna līnija, kas iet caur šo punktu, krusto otrās kārtas virsmu dubultā punktā vai ir virsmas taisnlīnijas ģenerātors.

3. teorēma. Otrās kārtas virsmas pieskares līnijas noteiktā nevienskaitļa punktā atrodas tajā pašā plaknē, ko sauc par pieskares plakni virsmai apskatāmajā punktā. Pieskares plaknes vienādojumam ir

Pierādījums. Ļaut , , ir parametriski vienādojumi taisnei, kas iet caur vienādojumā (1) dotās otrās kārtas virsmas nevienskaitļa punktu. Aizvietojot vienādojumu (1) , , vietā , , , mēs iegūstam:

Tā kā punkts atrodas uz virsmas (1), mēs atrodam arī no (3) vienādojuma (šī vērtība atbilst punktam ). Lai līnijas krustpunkts ar virsmu (1) būtu divkāršs vai taisne pilnībā atrastos uz virsmas, ir nepieciešams un pietiekami, lai tiktu izpildīta vienādība:

Ja tajā pašā laikā:

Tad taisnes krustpunkts ar virsmu (1) ir dubults. Un ja:

Tad līnija pilnībā atrodas uz virsmas (1).

No relācijām (4) un , , izriet, ka jebkura punkta koordinātas , , kas atrodas uz jebkura virsmas (1) pieskares, apmierina vienādojumu:

Un otrādi, ja kāda cita punkta koordinātas atbilst šim vienādojumam, tad vektora koordinātas , , atbilst sakarībai (4), kas nozīmē, ka līnija ir pieskares aplūkotajai virsmai.

Tā kā punkts ir virsmas (1) nevienskaitlis punkts, tad starp skaitļiem , ir vismaz viens, kas nav vienāds ar nulli; tātad vienādojums (5) ir pirmās pakāpes vienādojums attiecībā pret . Šis ir vienādojums plaknei, kas pieskaras virsmai (1) uz tās norādītā nevienskaitļa punktā.

Pamatojoties uz otrās kārtas virsmu kanoniskajiem vienādojumiem, ir viegli sastādīt pieskares plakņu vienādojumus elipsoīdam, hiperboloīdam utt. noteiktā vietā uz tiem.

viens). Elipsoīda pieskares plakne:

2). Pieskares plakne vienas un divu lokšņu hiperboloīdiem:

3). Pieskares plakne eliptiskajiem un hiperboliskajiem paraboloīdiem:

§ 161. Pieskares plaknes krustpunkts ar otrās kārtas virsmu.

Par ODSC koordinātu sākumpunktu, ass, ņemam otrās kārtas virsmas nevienskaitļa punktu un novietojam to plaknē, kas pieskaras virsmai punktā . Tad vispārīgajā virsmas vienādojumā (1) brīvais loceklis ir vienāds ar nulli: , un plaknes, kas pieskaras virsmai, vienādojumam vajadzētu izskatīties šādi: .

Bet plaknes vienādojumam, kas iet caur izcelsmi, ir šāda forma: .

Un, tā kā šim vienādojumam jābūt līdzvērtīgam vienādojumam , tad , , .

Tātad izvēlētajā koordinātu sistēmā virsmas vienādojumam (1) vajadzētu izskatīties šādi:

Un otrādi, ja , tad vienādojums (6) ir virsmas vienādojums, kas iet caur koordinātu sākumpunktu, un plakne ir šīs virsmas pieskares plakne punktā . Taisnes vienādojumam, pa kuru virsmas pieskares plakne punktā krusto virsmu (6), ir šāda forma:

Ja . Tas ir invariants invariantu teorijā otrās kārtas līnijām. (7) vienādojums

Šī ir otrā rinda. Pēc šīs rindas formas invariants ir , tāpēc:

Attiecībā uz , šeit ir divas iedomātas krustojošas līnijas.

Kad - divas reālas krustojošas līnijas.

Ja , bet vismaz viens no koeficientiem , , nav vienāds ar nulli, tad krustojuma līnija (7) ir divas sakrītošas ​​līnijas.

Visbeidzot, ja , tad lidmašīna

ir daļa no dotās virsmas, un tā pati virsma sadalās plakņu pāros

§ 162. Otrās kārtas virsmas eliptiski, hiperboliski vai paraboliski punkti.

1. Ļaujiet otrās kārtas virsmas pieskares plaknei kādā punktā to krustot pa divām iedomātām krustojošām taisnēm. Šajā gadījumā punktu sauc par virsmas elipsveida punktu.

2. Ļaujiet otrās kārtas virsmas pieskares plaknei kādā punktā to krustot pa divām reālām taisnēm, kas krustojas saskares punktā. Šajā gadījumā punktu sauc par virsmas hiperbolisko punktu.

3. Ļaujiet otrās kārtas virsmas pieskares plaknei kādā punktā to krustot pa divām sakrītošām taisnēm. Šajā gadījumā punktu sauc par virsmas parabolisko punktu.

4. teorēma.Ļaujiet otrās kārtas virsmu attiecībā pret ODSC dot ar vienādojumu (1), un šis vienādojums (1) ir reālas otrās kārtas nesadalošas virsmas vienādojums. Tad ja ; tad visi virsmas punkti ir eliptiski.

Pierādījums. Ieviesīsim jaunu koordinātu sistēmu , par koordinātu sākumpunktu izvēloties jebkuru dotās virsmas nevienskaitli punktu un novietojot asis un plaknē pieskares virsmai punktā . Vienādojums (1) jaunajā koordinātu sistēmā tiek pārveidots šādā formā:

Kur . Aprēķināsim šī vienādojuma invariantu.

Tā kā, pārejot no viena ODSC uz otru, zīme nemainās, tad zīmes un ir pretējas, tādēļ, ja , tad ; un, kā izriet no klasifikācijas (sk. 161. §), virsmas pieskares plakne punktā krusto virsmu pa divām iedomātām krustojošām taisnēm, t.i. ir eliptisks punkts.

2) Vienas lapas hiperboloīds un hiperboliskais paraboloīds sastāv no hiperboliskiem punktiem.

3) Otrās kārtas reālais konuss (virsotne ir izslēgta), eliptiskie (reālie), hiperboliskie un paraboliskie cilindri sastāv no paraboliskiem punktiem.

paraboliskais cilindrs.

Lai noteiktu paraboliskā cilindra atrašanās vietu, pietiek zināt:

1) simetrijas plakne, kas ir paralēla cilindra ģeneratoriem;

2) cilindra pieskares plakne, kas ir perpendikulāra šai simetrijas plaknei;

3) vektors, kas ir perpendikulārs šai pieskares plaknei un ir vērsts uz cilindra ieliekumu.

Ja vispārīgais vienādojums definē parabolisko cilindru, to var pārrakstīt šādi:

Izvēlēsimies m lai lidmašīna

būtu savstarpēji perpendikulāri:

Ar šo vērtību m lidmašīna

būs simetrijas plakne, kas ir paralēla cilindra ģeneratoriem.

Lidmašīna

būs cilindra pieskares plakne, kas ir perpendikulāra norādītajai simetrijas plaknei, un vektors

būs perpendikulāra atrastajai pieskares plaknei un vērsta pret cilindra ieliekumu.