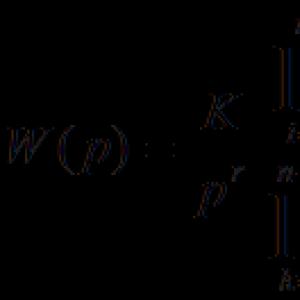Nyquist hodogrāfa konstrukcija. Amplitūdas fāzes raksturlielums (Nyquist hodogrāfs)

Kreisais hodogrāfs ir acīmredzami stabilas sistēmas hodogrāfs, neaptver punktus, kas ir nepieciešami saskaņā ar Nyquist kritēriju slēgtas cikla sistēmas stabilitātei. Labais hodogrāfs – hodogrāfs trīspolu, acīmredzami nestabila sistēma apiet lietu trīs reizes pretēji pulksteņrādītāja virzienam, kas ir nepieciešams saskaņā ar Nyquist kritēriju slēgta cikla sistēmas stabilitātei.

komentēt.

Sistēmu ar reāliem parametriem amplitūdas fāzes raksturlielumi - un tikai tādi ir sastopami praksē - ir simetriski attiecībā pret reālo asi. Tāpēc parasti tiek ņemta vērā tikai puse no amplitūdas fāzes raksturlielumiem, kas atbilst pozitīvajām frekvencēm. Šajā gadījumā tiek ņemti vērā punkta pusceļi. Segmenta () krustpunkts, kad frekvence palielinās no augšas uz leju (fāze palielinās), tiek uzskatīta par krustojumu, un no apakšas uz augšu tiek uzskatīts par krustojumu. Ja atvērtas cilpas sistēmas amplitūdas fāzes raksturlielums sākas segmentā (), tad tas atbilst vai nu krustojumam, atkarībā no tā, vai raksturlielums samazinās vai palielinās, palielinoties frekvencei.

Segmenta () krustpunktu skaitu var aprēķināt, izmantojot logaritmiskos frekvences raksturlielumus. Paskaidrosim, ka tie ir krustojumi, kas atbilst fāzei, kad amplitūdas raksturlieluma lielums ir lielāks par vienu.

Stabilitātes noteikšana, izmantojot logaritmiskos frekvences raksturlielumus.

Lai izmantotu Mihailova kritēriju, jums ir jākonstruē hodogrāfs. Šeit ir raksturīgais slēgtās sistēmas polinoms.

Nyquist kritērija gadījumā pietiek zināt atvērtās cilpas sistēmas pārsūtīšanas funkciju. Šajā gadījumā nav nepieciešams konstruēt hodogrāfu. Lai noteiktu Nyquist stabilitāti, pietiek ar atvērtās cilpas sistēmas logaritmisko amplitūdas un fāzes frekvences raksturlielumu konstruēšanu.

Vienkāršākā konstrukcija tiek iegūta, ja atvērtas cilpas sistēmas pārneses funkciju var attēlot formā

, tad LAH ,

Zemāk redzamais attēls atbilst pārsūtīšanas funkcijai

.

Šeit un veidota kā funkcijas.

Tālāk parādītie logaritmiskie frekvences raksturlielumi atbilst iepriekš minētajai sistēmai ar pārsūtīšanas funkciju (atvērtās cilpas sistēma)

.

Kreisajā pusē ir pārsūtīšanas funkcijas amplitūdas un fāzes frekvences raksturlielumi, labajā pusē - pārsūtīšanas funkcijai, centrā - sākotnējai pārsūtīšanas funkcijai (kā aprēķināts ar Les programmu, “Integrācijas” metode).

Trīs funkcijas stabi ir nobīdīti pa kreisi (stabila sistēma). Fāzes raksturlielumam attiecīgi ir 0 līmeņu krustojumu. Trīs funkcijas stabi ir nobīdīti pa labi (nestabila sistēma). Attiecīgi fāzes raksturlielumam ir trīs puslīmeņa krustojumi apgabalos, kur pārneses funkcijas modulis ir lielāks par vienību.

Jebkurā gadījumā slēgtā sistēma ir stabila.

Centrālais attēls - aprēķins, ja nav sakņu kustību, ir labā attēla robeža, fāzes gaita kreisajā attēlā ir radikāli atšķirīga. Kur ir patiesība?

Piemēri no.

Ļaujiet atvērtās cilpas sistēmas pārsūtīšanas funkcijai būt šādā formā:

.

Atvērtā cikla sistēma ir stabila jebkuram pozitīvam k Un T. Slēgta sistēma ir arī stabila, kā redzams no hodogrāfa attēla kreisajā pusē.

Kad negatīvs T atvērtā cikla sistēma ir nestabila - tai ir pluss labajā pusplaknē. Slēgtā sistēma ir stabila pie , kā redzams no hodogrāfa centrā, un nestabila pie (hodogrāfs labajā pusē).

Ļaujiet atvērtās cilpas sistēmas pārsūtīšanas funkcijai būt šādā formā ():

.

Tam ir viens stabs uz iedomātās ass. Līdz ar to slēgtas cilpas sistēmas stabilitātei ir nepieciešams, lai reālās ass segmenta () krustpunktu skaits ar atvērtās cilpas sistēmas amplitūdas fāzes raksturlielumu būtu vienāds (ja ņemam vērā tikai hodogrāfu pozitīvām frekvencēm).

Svarīga teorēma no kompleksa mainīgā funkciju teorijas nosaka: lai funkcija ir unikāla vienkārši savienotā kontūrā C un turklāt ir unikāla un analītiska uz šīs kontūras. Ja uz C nav vienāds ar nulli un ja kontūras C iekšpusē var būt tikai ierobežots skaits vienskaitļu punktu (polu), tad

kur ir nulles skaits un polu skaits C iekšpusē, no kuriem katrs tiek ņemts vērā atkarībā no tā daudzuma.

Šī teorēma tieši izriet no Košī atlikuma teorēmas, kurā teikts, ka

Aizstāsim ar un atzīmēsim, ka singularitātes tiek saglabātas gan nullēs, gan polios. Tad šajos vienskaitļa punktos atrastie atlikumi būs vienādi ar vienskaitļa punktu reizinājumiem ar pozitīvu zīmi pie nullēm un negatīvu zīmi pie nulles. stabi Iepriekš formulētā teorēma tagad ir acīmredzama.

Attiecības (11.2-1) var ierakstīt arī formā

Tā kā kontūrai C parasti ir gan reālas, gan iedomātas daļas, tās logaritms tiks rakstīts formā

Ja C nepazūd nekur uz robežas, integrācija (II.2-3) dod tieši

kur apzīmē patvaļīgu slēgtās kontūras C sākumu un beigas.

Apvienojot rezultātus (II.2-1) un (II.2-7), mēs atklājam, ka kopējo leņķa izmaiņu reizinājums (pilnīgs apgrieziens ap sākuma punktu), kad kontūra C iet apkārt, ir vienāda ar starpību starp nulles un stabi kontūras C iekšpusē.

Ja ir kopējais apgriezienu skaits ap izcelsmi, kad C skrien apkārt, tad mēs varam rakstīt

Turklāt kontūra C iet apkārt virzienā, kas atbilst pozitīvā leņķa pieaugumam, un apgriezienu sauc par pozitīvu, ja tas notiek arī virzienā, kas atbilst pozitīvā leņķa pieaugumam.

Rīsi. II.2-1. Slēgta kontūra, kas aptver labās pusplaknes galīgo daļu.

Tagad šos rezultātus var tieši pielietot stabilitātes noteikšanas problēmai. Mēs vēlamies zināt, vai pārsūtīšanas funkcijas saucējam ir nulles labajā pusplaknē.

Līdz ar to kontūra C ir izvēlēta tā, lai pilnībā aptvertu labo pusplakni. Šī shēma ir parādīta attēlā. kur lielo pusloku, kas aptver labo pusplakni, dod attiecības

vienlaikus tiecoties uz bezgalību robežās.

Pieņemsim, ka tas ir uzrakstīts kā

kur ir visa funkcija un kam nav kopīgu faktoru. Tālāk konstruēsim diagrammu kompleksajā plaknē, mainot vērtības gar kontūru C. Šī diagramma sniegs mums kādu slēgtu kontūru. Vispārīgā gadījumā tā būs vesela polinoma formas funkcija, kurai plaknes galīgajā daļā acīmredzami nav polu. Ja tas ir pārpasaulīgs, tad ir jānosaka polu skaits P labās pusplaknes galīgajā daļā. Zinot P un no diagrammas nosakot, kad C iet cauri, tagad saskaņā ar vienādojumu (II.2-8) varam noteikt nulles punktu skaitu labajā pusplaknē

Rīsi. II.2-2. Vienkārša vienas ķēdes vadības sistēma.

Lai sistēma būtu stabila, tai jābūt vienādai ar nulli. Līdz ar to šī kritērija piemērošana ietver divus posmus: pirmais ir polu noteikšana labajā pusplaknē, bet otrais ir diagrammas konstruēšana, kad cauri iet C. Pirmo posmu parasti veic ļoti vienkārši. Otrais var radīt ievērojamas grūtības, īpaši, ja tas ir trešās vai augstākas pakāpes un satur pārpasaulīgus terminus.

Atgriezeniskās saites vadības sistēmai, kas vispārīgā veidā parādīta attēlā. Diagrammu veidošanas sarežģītību var ievērojami samazināt, izmantojot atvērtās cilpas pārsūtīšanas funkciju. Slēgta cikla sistēmas pārsūtīšanas funkcija ir saistīta ar atvērta cikla sistēmas pārsūtīšanas funkciju ar attiecību

kur var būt gan stabi, gan nulles. Stabilitātes problēmas gadījumā ir vēlams zināt, vai tai ir stabi labajā pusplaknē. Tas ir līdzvērtīgs atrašanās funkcijas nulles labajā pusplaknē vai atrašanās labajā pusplaknē, kas nobīdīta par -1, funkcijas nullēm. Lai noskaidrotu efektu, kas rodas, mainoties funkcijas nullēm. atvērtās cilpas pastiprinājumu, un tajā pašā laikā minimizējot Nikvista diagrammas konstruēšanas darbu, saucēju izteiksmes (II.2-12) pārrakstām formā, kur K ir atvērtās cilpas sistēmas pastiprinājums. Tagad stabi ir identiski nullēm attiecībā pret

Lai pielietotu Nyquist kritēriju, vispirms uzzīmējam kontūru C, kas aptver

visa labā pusplakne. Pēc tam mēs aprēķinām kopējo apgriezienu skaitu vienai un tai pašai kustībai ap punktu Mainot pastiprinājumu K maina tikai punkta pozīciju un neietekmē atrašanās vietu [-Noteikts PPP funkcijas polu skaits P tieši no pašas funkcijas, ja tai ir vienkāršu faktoru reizinājuma forma, vai grūtāk aprēķināt, ja tai ir polinoma vai transcendentāla forma. Pēc tam sistēmas stabilitāti nosaka, tieši piemērojot vienādojumu (II.2-8), kas nosaka

Līdz ar to sistēma ir stabila tikai tad, ja tā ir vienāda ar nulli, kur tagad saucēja nulles skaits (II.2-12)

Rīsi. II.2-3. Divas iespējamās ķēžu modifikācijas ar stabu apvadīšanu uz iedomātās ass.

Piemērojot kritēriju šajā formā, uzmanība jāpievērš kontūras C izvēlei, kas aptver labo pusplakni. Attiecības (11.2-1) un līdz ar to (11.2-13) prasa, lai kontūrā C nebūtu redzamas funkcijas singularitātes. Bieži ir gadījumi, kad tās sākumā ir pols vai pat vairāki sarežģītu konjugētu polu pāri uz kontūras. iedomātā ass. Lai risinātu šos īpašos gadījumus, kongur C tiek modificēts, šķērsojot katru no singularitātēm ļoti mazos puslokos, kā parādīts attēlā. II.2-3. Ja pazīmes ir stabi, tad modificētā kontūra C var iet vai nu pa labi, vai pa kreisi no tiem, kā parādīts attēlā. Attiecīgi II.2-3,a un II.2-3,b. Ja singularitāte nav pols, tad kontūrai vienmēr jāiet pa labi no tā, jo relācija (II.2-1) pieļauj tikai tādas singularitātes kā stabi kontūras C iekšpusē. Tie stabi uz iedomātās ass, kas tiek apieti no kreisās puses, atrodas kontūras C iekšpusē un tāpēc ir jāņem vērā P. Šajā gadījumā kontūru C tiešā vienskaitļa punkta tuvumā parasti izvēlas formā.

kur leņķis mainās no līdz robežās, ir tendence uz nulli.

Hodogrāfs, šķērsojot kontūru C, sastāv galvenokārt no četrām daļām. Hodogrāfs plkst

izslēdzot singularitātes tuvumu uz iedomātās ass, ir vienkārši atvērtās cilpas sistēmas frekvences reakcija. Tāpēc hodogrāfu pie var iegūt, uzzīmējot to pie attiecībā pret reālo asi. Kad viens iet cauri bezgalīgam puslokam, visu fiziski īstenojamo sistēmu vērtība ir nulle vai, augstākais, ierobežota konstanta vērtība. Visbeidzot, hodogrāfs, skrienot pa maziem puslokiem stabu tuvumā uz iedomātas ass, tiek noteikts, tieši aizstājot izteiksmi (II.2-14) šajā funkcijā. Tādējādi kontūras C kartēšana funkcijas plaknē ir pabeigta.

Piemērojot kritēriju šādā formā, kļūst acīmredzams tam noteikto ierobežojumu raksturs. Pirmkārt, tai var būt tikai ierobežots skaits polu tipa singularitātes labajā pusplaknē. Otrkārt, tam var būt tikai ierobežots skaits singularitātes (polu vai atzaru punktu) uz iedomātās ass. Funkciju klasi var paplašināt, iekļaujot funkcijas, kurām ir atzarojuma punkti, ja vien atzarojuma punkti atrodas kreisajā pusplaknē un ja tiek izmantota funkcijas galvenā vērtība. Treškārt, ir pieļaujamas nozīmīgas formas pazīmes skaitītājā, jo šīs funkcijas absolūtā vērtība, mainoties labajā pusplaknē, atrodas starp un 0.

Ieteicams ar piemēru demonstrēt Nyquist kritērija piemērošanu. Ļaujiet kontrolēto sistēmu ar atgriezenisko saiti definēt ar attiecībām

Doto elementu pārneses funkcija atbilst divfāzu asinhronajam motoram, kas darbojas ar frekvenci no pusviļņa magnētiskā pastiprinātāja. Negatīvās amortizācijas klātbūtne ir saistīta ar zemu rotora pretestību. Rodas pirmais jautājums: vai dotos elementus ir iespējams stabilizēt tikai pastiprinājuma koeficienta dēļ? Tāpēc liksim

Atvērtās cilpas sistēmas pārsūtīšanas funkcija izpaužas formā

Mēs redzam, pirmkārt, ka tai ir tikai viens stabs labajā pusplaknē un šis pols atrodas punktā Aptuvenā diagramma, izskrienot kontūru C, kas parādīta attēlā. II.2-4, a, ir parādīts attēlā. II.2-4, b un parāda, ka pie izvēlētā pastiprinājuma ir viens pozitīvs apgrieziens ap punktu.

Rīsi. II.2-4. Nyquist diagrammu piemēri.

Tāpēc, izmantojot Nikvista kritēriju, kas izteikts ar vienādojumu (II.2-13), mēs nonākam pie rezultāta

Palielinot K, tiek radīta lielāka pozitīvu apgriezienu skaita iespēja, jo diagrammas daļa ir spirālveida reizinātāja dēļ, tāpēc mēs varam secināt, ka sistēma ir nestabila visām pozitīvajām K vērtībām.

Negatīvām K vērtībām mēs varam vai nu pagriezt diagrammu attiecībā pret izcelsmi un ņemt vērā apgriezienus ap punktu, vai arī izmantot esošu diagrammu un apsvērt apgriezienus ap punktu. Pēdējā metode ir vienkāršāka; tas tieši parāda, ka vismaz nekādu pozitīvu notikumu apkārt nav. Tas dod vismaz vienu nulli labajā pusplaknē K negatīvajām vērtībām. Tāpēc mēs secinām, ka sistēma ir nestabila visām K vērtībām, gan pozitīvajām, gan negatīvajām, un tāpēc ir nepieciešama korekcija, lai veiktu sistēma stabila.

Nyquist kritēriju var izmantot arī tad, ja atvērtās cilpas sistēmas frekvences reakcija tiek konstruēta no eksperimentāliem datiem. Atvērtās cilpas sistēmas pārneses funkcijai šajā gadījumā jābūt stabilai, un tāpēc tai nedrīkst būt stabi labajā pusplaknē, t.i. Lai pareizi izveidotu Nyquist hodogrāfu, rūpīgi jānosaka sistēmas darbība ļoti zemās frekvencēs.

Piemērojot Nyquist kritēriju vairāku cilpu sistēmām, konstrukcija sākas ar visdziļāko cilpu un turpinās līdz ārējām cilpām, rūpīgi saskaitot PPP stabu skaitu no katras atsevišķas cilpas. Šajā metodē ieguldīto darbu bieži var samazināt, likvidējot dažas ķēdes, pārveidojot blokshēmu. Daudzcilpu sistēmu hodogrāfa konstruēšanas secības izvēle ir atkarīga no konstrukcijas diagrammas, kā arī no noteikto un koriģējošo elementu izvietojuma kontūrās.

Tas ir to punktu lokuss, kurus apraksta frekvences pārnešanas funkcijas vektora beigas, kad frekvence mainās no -∞ uz +∞. Segmenta izmērs no sākuma līdz katram hodogrāfa punktam parāda, cik reizes noteiktā frekvencē izejas signāls ir lielāks par ieejas signālu, un fāzes nobīdi starp signāliem nosaka leņķis pret minēto segmentu.

Visas pārējās frekvences atkarības tiek ģenerētas no AFC:

• U(w) - vienmērīga (slēgtām automātiskās vadības sistēmām P(w));
• V(w) - nepāra;
• A(w) - vienmērīga (frekvences reakcija);
• j(w) - nepāra (fāzes reakcija);
• LACHH & LFCH - izmanto visbiežāk.

Logaritmiskās frekvences raksturlielumi.

Logaritmiskās frekvences raksturlielumi (LFC) ietver logaritmisko amplitūdas raksturlielumu (LAFC) un logaritmiskās fāzes raksturlīkni (LPFC), kas atsevišķi konstruēti vienā plaknē. LFC un LFCH konstrukcija tiek veikta, izmantojot šādas izteiksmes:

L(w) = 20 lg | W(j w)| = 20 lg A(w), [dB];

j(w) = arg( W(j w)), [rad].

Lielums L(w) ir izteikts decibeli . Bel ir logaritmiska vienība, kas atbilst desmitkārtīgam jaudas pieaugumam. Viens Bels atbilst jaudas palielinājumam 10 reizes, 2 Bels - 100 reizes, 3 Bels - 1000 reizes utt. Decibels ir vienāds ar vienu desmito daļu no Bela.

AFC, AFC, PFC, LFC un LPFC piemēri tipiskām dinamiskām saitēm ir sniegti 2. tabulā.

2. tabula. Tipisku dinamisko saišu frekvences raksturlielumi.

Automātiskās regulēšanas principi

Pamatojoties uz vadības principu, pašpiedziņas pistoles var iedalīt trīs grupās:

1. Ar regulēšanu, kas balstīta uz ārējām ietekmēm - Poncelet princips (izmanto atvērtas cilpas pašpiedziņas lielgabalos).
2. Ar regulēšanu ar novirzi - Polzunova-Watt princips (izmanto slēgtās pašpiedziņas pistolēs).
3. Ar kombinēto regulējumu. Šajā gadījumā ACS ir slēgtas un atvērtas vadības cilpas.

Kontroles princips balstās uz ārējiem traucējumiem

Struktūrai nepieciešami traucējumu sensori. Sistēmu apraksta atvērtās cilpas pārsūtīšanas funkcija: x(t) = g(t) - f(t).

Priekšrocības:

• Ir iespējams panākt pilnīgu invarianci pret noteiktiem traucējumiem.
• Sistēmas stabilitātes problēma nerodas, jo nav OS.

Trūkumi:

• Lielam skaitam traucējumu nepieciešams atbilstošs kompensācijas kanālu skaits.
• Izmaiņas vadāmā objekta parametros noved pie vadības kļūdām.
• Var attiecināt tikai uz objektiem, kuru īpašības ir skaidri zināmas.

Noviržu kontroles princips

Sistēmu apraksta ar atvērtās cilpas pārsūtīšanas funkciju un slēgšanas vienādojumu: x(t) = g(t) - y(t) W oc( t). Sistēmas algoritms ir balstīts uz vēlmi samazināt kļūdu x(t) uz nulli.

Priekšrocības:

• OOS noved pie kļūdu samazināšanās, neatkarīgi no faktoriem, kas to izraisījuši (kontrolējamā objekta parametru vai ārējo apstākļu izmaiņas).

Trūkumi:

• OS sistēmās pastāv stabilitātes problēma.
• Principā nav iespējams panākt absolūtu invarianci pret traucējumiem sistēmās. Vēlme panākt daļēju nemainīgumu (ne ar pirmo OS) noved pie sistēmas sarežģījumiem un stabilitātes pasliktināšanās.

Kombinētā vadība

Kombinētā vadība sastāv no divu vadības principu kombinācijas, kuras pamatā ir novirze un ārējie traucējumi. Tie. Vadības signālu objektam ģenerē divi kanāli. Pirmais kanāls ir jutīgs pret kontrolētā mainīgā novirzi no mērķa. Otrais ģenerē vadības darbību tieši no galvenā vai traucējošā signāla.

x(t) = g(t) - f(t) - y(t)Woc(t)

Priekšrocības:

• OOS klātbūtne padara sistēmu mazāk jutīgu pret kontrolējamā objekta parametru izmaiņām.
• Atsauces vai traucējumu jutīga kanāla(-u) pievienošana neietekmē atgriezeniskās saites cilpas stabilitāti.

Trūkumi:

• Kanāli, kas ir jutīgi pret uzdevumu vai traucējumiem, parasti satur atšķirīgas saites. To praktiskā īstenošana ir sarežģīta.
• Ne visi objekti pieļauj piespiešanu.

ATS stabilitātes analīze

Regulatīvās sistēmas stabilitātes jēdziens ir saistīts ar tās spēju atgriezties līdzsvara stāvoklī pēc ārējo spēku izzušanas, kas to izveda no šī stāvokļa. Stabilitāte ir viena no galvenajām prasībām automātiskajām sistēmām.

Stabilitātes jēdzienu var attiecināt arī uz ATS kustības gadījumu:

• netraucēta kustība
• sašutusi kustība.

Jebkuras vadības sistēmas kustība tiek aprakstīta, izmantojot diferenciālvienādojumu, kas kopumā raksturo 2 sistēmas darbības režīmus:

Līdzsvara režīms

Braukšanas režīms

Šajā gadījumā vispārējo risinājumu jebkurā sistēmā var uzrakstīt šādi:

Piespiedu kārtā komponentu nosaka ievades ietekme uz vadības sistēmas ievadi. Sistēma šo stāvokli sasniedz pārejošu procesu beigās.

Pārejas komponentu nosaka, atrisinot homogēnu diferenciālvienādojumu formā:

Koeficienti a 0 ,a 1 ,…a n ietver sistēmas parametrus => jebkura diferenciālvienādojuma koeficienta maiņa noved pie vairāku sistēmas parametru izmaiņām.

Homogēna diferenciālvienādojuma atrisinājums

kur ir integrācijas konstantes un šādas formas raksturīgā vienādojuma saknes:

Raksturīgais vienādojums attēlo pārsūtīšanas funkcijas saucēju, kas vienāds ar nulli.

Raksturīgā vienādojuma saknes var būt reāls, komplekss konjugāts un komplekss, ko nosaka sistēmas parametri.

Lai novērtētu sistēmu stabilitāti, vairākas ilgtspējības kritēriji

Visi ilgtspējības kritēriji ir iedalīti 3 grupās:

Sakne

- algebriskā

Uzdevuma nosacījums.

Izmantojot Mihailova un Nyquist stabilitātes kritēriju, nosakiet vienas cilpas vadības sistēmas stabilitāti, kurai ir formas pārsūtīšanas funkcija atvērtā stāvoklī

Ievadiet K, a, b un c vērtības formulā atbilstoši opcijai.

W(s) = , (1)

Konstruēt Mihailova un Nyquist hodogrāfus. Nosakiet sistēmas izslēgšanas frekvenci.

Nosakiet sistēmas pastiprinājuma kritisko vērtību.

Risinājums.

Vadības sistēmu analīzes un sintēzes problēmas tiek risinātas, izmantojot tādu jaudīgu matemātisko aparātu kā operacionālais aprēķins (Laplasa transformācija). Vadības sistēmu analīzes un sintēzes problēmas tiek risinātas, izmantojot tādu jaudīgu matemātisko aparātu kā operacionālais aprēķins (Laplasa transformācija). Operatora vienādojuma vispārīgais risinājums ir terminu summa, ko nosaka raksturīgā polinoma (polinoma) sakņu vērtības:

D(s) =  d s n d n ) .

Mihailova hodogrāfa uzbūve.

A) Mēs izrakstām raksturīgo polinomu slēgtai sistēmai, kas aprakstīta ar vienādojumu (1)

D(s) = 50 + (25s+1)(0,1s+1)(0,01s+1) = 50+(625+50s+1)(0,001+0,11s+1) =0,625+68,85 +630,501+50,11 +51.

Polinoma saknes D(s) var būt: null; reāls (negatīvs, pozitīvs); iedomāts (vienmēr savienots pārī, konjugēts) un komplekss konjugāts.

B) Pārveido formā s→ ωj

D()=0,625+68,85+630,501+50,11+51=0,625ω-68,85jω- 630,501ω+50,11jω+51

ω – signāla frekvence, j = (1) 1/2 – iedomātā vienība. J 4 = (-1) 4/2 = 1, J 3 = (-1) 3/2 =-(1) 1/2 = - j, J 2 = (-1) 2/2 = -1, J = (-1) 1/2 = j,

C) Atlasīsim reālās un iedomātās daļas.

D= U()+jV(), kur U() ir reālā daļa un V() ir iedomātā daļa.

U(ω) =0,625ω-630,501ω+51

V(ω) =ω(50,11-68,85ω)

D) Uzbūvēsim Mihailova hodogrāfu.

Izveidosim Mihailova hodogrāfu tuvu nullei un prom no nulles; šim nolūkam mēs izveidosim D(jw), kad w mainīsies no 0 uz +∞. Atradīsim krustošanās punktus U(zizlis V w) ar asīm. Atrisināsim problēmu, izmantojot Microsoft Excel.

Mēs iestatām w vērtības diapazonā no 0 līdz 0,0001 līdz 0,1 un aprēķinām tās tabulā. Excel vērtības U(ω) un V(ω), D(ω); atrodiet krustojuma punktus U(zizlis V w) ar asīm,

Mēs iestatām w vērtības diapazonā no 0,1 līdz 20 un aprēķinām tās tabulā. Excel vērtības U(zizlis V(w), D; atrodiet krustojuma punktus U(zizlis V w) ar asīm.

2.1. tabula. Reālās un iedomātās daļas un paša polinoma definīcija D()izmantojot Microsoft Excel

Rīsi. A, B, ..... Atkarības U(ω) un V(ω), D(ω) no ω

Saskaņā ar att. A, B, .....atrodiet krustošanās punktus U(zizlis V w) ar asīm:

pie ω = 0 U(ω)= …. Un V(ω)= ……

1. att. Mihailova hodogrāfs pie ω = 0:000,1:0,1.

2. att. Mihailova hodogrāfs pie ω = 0,1:20

D) Secinājumi par sistēmas stabilitāti, pamatojoties uz hodogrāfu.

Jebkuras dinamiskas sistēmas stabilitāti (kā jēdzienu) nosaka tās uzvedība pēc ārējās ietekmes noņemšanas, t.i. tā brīva kustība sākotnējo apstākļu ietekmē. Sistēma ir stabila, ja tā atgriežas sākotnējā līdzsvara stāvoklī pēc tam, kad signāls (traucējums), kas to izvedis no šī stāvokļa, pārstāj iedarboties uz sistēmu. Nestabila sistēma neatgriežas sākotnējā stāvoklī, bet laika gaitā nepārtraukti attālinās no tā. Lai novērtētu sistēmas stabilitāti, ir jāizpēta dinamikas vienādojuma risinājuma brīvā sastāvdaļa, tas ir, vienādojuma atrisinājums:.

D(s) =  d s n d n )= 0.

Pārbaudiet sistēmas stabilitāti, izmantojot Mihailova kritēriju :

Mihailova kritērijs: Lai nodrošinātu stabilu ASR, ir nepieciešams un pietiekami, lai Mihailova hodogrāfs (sk. 1. un 2. att.), sākot no w = 0 uz pozitīvās reālās pusass, secīgi griežas pozitīvā virzienā (pretēji pulksteņrādītāja virzienam) kā w palielinās no 0 līdz ∞ n kvadrantiem, kur n ir raksturīgā polinoma pakāpe.

No risinājuma (sk. 1. un 2. att.) ir skaidrs, ka hodogrāfs atbilst šādiem kritērija nosacījumiem: Tas sākas uz pozitīvās reālās pusass pie w = 0. Hodogrāfs neatbilst šādiem kritērija nosacījumiem: it neapiet visus 4 kvadrantus pozitīvā virzienā (polinoma pakāpe n=4) pie ω.

Mēs secinām, ka šī atvērtā cikla sistēma nav stabila .

Nyquist hodogrāfa uzbūve.

A) Veiksim aizstāšanu formulā (1) s → ωj

W(s) = =,

B) Atveriet iekavas un izceliet saucējā reālās un iedomātās daļas

C) Reiziniet ar konjugātu un atlasiet reālās un iedomātās daļas

,

kur U() ir reālā daļa un V() ir iedomātā daļa.

D) Konstruēsim Nikvista hodogrāfu: - W() atkarība no .

3. att. Nyquist hodogrāfs.

E) Pārbaudīsim sistēmas stabilitāti, izmantojot Nyquist kritēriju:

Nyquist kritērijs: Lai sistēma, kas ir stabila atvērtā stāvoklī, būtu stabila slēgtā stāvoklī, ir nepieciešams, lai Nyquist hodogrāfs, kad frekvence mainās no nulles uz bezgalību, nepārklāj punktu ar koordinātām (-1; j0) .

No risinājuma (sk. 3. att.) ir skaidrs, ka hodogrāfs atbilst visiem kritērija nosacījumiem:

Hodogrāfs maina virzienu pulksteņrādītāja virzienā

Hodogrāfs neaptver punktu (-1; j0)

Mēs secinām, ka šī atvērtā cikla sistēma ir stabila .

Sistēmas pastiprinājuma kritiskās vērtības noteikšana.

A) 2. punktā jau ir nošķirtas reālās un iedomātās daļas

B) Lai atrastu sistēmas pastiprinājuma kritisko vērtību, ir nepieciešams pielīdzināt iedomāto daļu nullei un reālo daļu -1

C) Atradīsim no otrā (2) vienādojuma

Skaitītājam jābūt 0.

Tad mēs to pieņemam

C) Aizstājiet pirmo (1) vienādojumu un atrodiet

Sistēmas pastiprinājuma kritiskā vērtība.

Literatūra:

1. Automātiskās vadības klasiskās un modernās teorijas metodes. 1. sējums.

Automātiskās vadības sistēmu analīze un statistiskā dinamika. M: Ed. MSTU nosaukts Baumaņa vārdā. 2000. gads

2. Voronovs A.A. Automātiskās vadības teorija. T. 1-3, M., Nauka, 1992.g