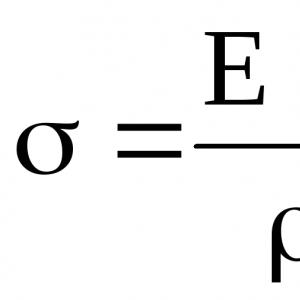Kas ir bīdes spriegums. locīt

Plakans (taisns) līkums- kad lieces moments iedarbojas plaknē, kas iet caur vienu no sekcijas galvenajām centrālajām inerces asīm, t.i. visi spēki atrodas stara simetrijas plaknē. Galvenās hipotēzes(pieņēmumi): garenšķiedru nespiediena hipotēze: šķiedras, kas ir paralēlas sijas asij, piedzīvo stiepes-spiedes deformāciju un neizdara viena uz otru šķērsvirzienā spiedienu; plakano sekciju hipotēze: sijas posms, kas pirms deformācijas ir plakans, pēc deformācijas paliek plakans un normāls pret sijas izliekto asi. Plakanas lieces gadījumā vispārējā gadījumā iekšējie stiprības faktori: gareniskais spēks N, šķērsspēks Q un lieces moments M. N>0, ja gareniskais spēks ir stiepes; pie M>0 šķiedras no augšas sijas tiek saspiestas, no apakšas tiek izstieptas. .

Tiek saukts slānis, kurā nav pagarinājumu neitrāls slānis(ass, līnija). Ja N=0 un Q=0, mums ir gadījums tīrs līkums. Normāli spriegumi:
, ir neitrālā slāņa izliekuma rādiuss, y ir attālums no kādas šķiedras līdz neitrālajam slānim.

43) Ekscentriskā spriedze un saspiešana

Spriedze un saspiešana

 - normāls spriegums[Pa], 1Pa (paskāls) \u003d 1 N / m 2,

10 6 Pa \u003d 1 MPa (megapaskāls) \u003d 1 N / mm 2

N - gareniskais (normālais) spēks [N] (ņūtons); F — šķērsgriezuma laukums [m 2]

 - relatīvā deformācija [bezizmēra vērtība];

L - garendeformācija [m] (absolūtais pagarinājums), L - stieņa garums [m].

-Hūka likums -  = E

E - stiepes modulis (1. veida elastības modulis jeb Janga modulis) [MPa]. Tēraudam E = 210 5 MPa = 210 6 kg / cm 2 ("vecajā" mērvienību sistēmā).

(jo vairāk E, jo mazāk izstiepjams materiāls)

;
- Huka likums

EF - stieņa stīvums stiepē (saspiešana).

Stienis tiek izstiepts, tas "novājinās", tā platums - a samazinās ar šķērsdeformāciju - a.

-relatīvā šķērsdeformācija.

-Puasona koeficients [bezdimensiju vērtība];

 svārstās no 0 (korķis) līdz 0,5 (gumija); tēraudam  0,250,3.

Ja gareniskais spēks un šķērsgriezums nav nemainīgi, tad stieņa pagarinājums:

Stiepes darbs:
, potenciālā enerģija:

47.Mora integrālis

Universāla metode pārvietojumu (lineāro un rotācijas leņķu) noteikšanai ir Mora metode. Sistēmai tiek pielikts viens vispārināts spēks punktā, kuram tiek meklēta vispārēja nobīde. Ja nosaka izlieci, tad vienības spēks ir bezizmēra koncentrēts spēks, ja nosaka griešanās leņķi, tad tas ir bezizmēra vienības moments. Telpiskās sistēmas gadījumā ir sešas iekšējo spēku sastāvdaļas. Ģeneralizētā nobīde ir noteikta

48. Sprieguma noteikšana kombinētās lieces un vērpes iedarbībā

Liekšana ar pagriezienu

Liekšanas un vērpes kopīga darbība ir visizplatītākais slodzes vārpstu gadījums. Ir piecas iekšējo spēku sastāvdaļas: Q x , Q y , M x , M y , M z =M cr. Aprēķinot, tiek veidoti lieces M x , M y un griezes momenta M cr momentu grafiki un noteikts bīstamais posms. Iegūtais lieces moments
. Maks. normālie un bīdes spriegumi bīstamos punktos (A, B):
,

, (aplim: W=
– aksiālais pretestības moments , W p =
- sekcijas polārais pretestības moments).

Galvenie spriegumi visbīstamākajos punktos (A un B):

Stiprības pārbaude tiek veikta saskaņā ar vienu no stiprības teorijām:

IV.: Mora teorija:

kur m=[ p ]/[ c ] – pieļaut. piemēram, spriegošana / saspiešana (trausliem materiāliem - čugunam).

T
.k.W p =2W, mēs iegūstam:

Skaitītājs ir samazinātais moments saskaņā ar pieņemto spēka teoriju. ;

II.: , ar Puasona koeficientu =0,3;

III-I:

vai viena formula:
, no kurienes pretestības moments:
, vārpstas diametrs:
. Formulas ir piemērotas arī gredzenveida sekcijas aprēķināšanai.

Aktīvā, reaktīvā un šķietamā jauda ķēdēs ar nesinusoidālu periodisku spriegumu un strāvu.

Antivielas kā adaptīvās imunitātes humorālās saites galvenās efektormolekulas

Rodas Apollonijs un Homēra eposa atdzimšana. "Argonautika" - sižets, kompozīcija, galvenie attēli. Stila iezīmes.

Ardha matsyendrasana - nepilnīga karaliskā zivju poza vai mugurkaula sagriešanās

Kādā gadījumā tiek veikta darbinieku zināšanu ārpuskārtas pārbaude?

Sprieguma sliekšņa vērtība un tās regulēšanas veidi

Vispārīgā gadījumā lieces laikā jebkurš sijas punkts atrodas vienkāršotā plaknes sprieguma stāvoklī (1.14. attēls), pa kura malām darbojas gan normālie, gan bīdes spriegumi.

Atrisinot apgriezto uzdevumu šādam saspīlētam stāvoklim, var atrast galvenā laukuma a o pozīciju un galveno spriegumu vērtības σ 1, σ 3 saskaņā ar šādām atkarībām

Analizēsim sijas bīstamo punktu sprieguma stāvokli. Lai to izdarītu, apsveriet vienkārša sijas aprēķina shēmu ar šķērsspēka Q un lieces momenta M diagrammām (1.15. Attēls). Pamatojoties uz šīs sijas sekcijas augstumu, mēs konstruējam normālo, tangenciālo un galveno spriegumu diagrammas, ņemot vērā atkarības (1.8) - (1.10).

Vispārīgā gadījumā pilna sijas lieces stiprības pārbaude tiek veikta saskaņā ar sekojošo trīs veidu bīstamības punkti .

I tipa bīstamie punkti: visā sijas garumā atrodas posmos, kur iedarbojas maksimālā absolūtā lieces momenta vērtība (I-I sadaļa), bet gar sijas augstumu - sekcijas galējās šķiedrās, kur rodas maksimālie normālie spriegumi (1. un 5). Šajos punktos rodas lineārs sprieguma stāvoklis. Stiprības nosacījums I tipa punktiem ir šāds ( galvenais stiprības stāvoklis)

II tipa bīstamības punkti atrodas gar sijas garumā sekcijās ar maksimālo šķērsspēku (II-II sadaļa pa kreisi un pa labi), un gar sijas augstumu - neitrālās līnijas līmenī (3. punkts pa kreisi un pa labi), kur maksimālā bīde stresa akti. Šajos punktos rodas īpašs plaknes sprieguma stāvokļa gadījums - tīra bīde. Stiprības nosacījumam ir šāda forma:

III tipa bīstamības punkti atrodas sijas posmos, kur rodas nelabvēlīga liela lieces momenta un šķērsspēka kombinācija (III-III sadaļa pa kreisi un pa labi), un pa sijas augstumu - starp galējām šķiedrām un neitrālo līniju, kur gan normālā, gan bīdes spriegumi vienlaikus ir lieli (2. un 4. punkts pa kreisi, pa labi). Šajos punktos rodas vienkāršots plaknes sprieguma stāvoklis. Stiprības nosacījumu III tipa punktiem raksta pēc stiprības teorijas (piemēram, plastmasas materiālam: pēc III vai IV teorijas).

Ja, veicot aprēķinus, izturība saskaņā ar kādu no nosacījumiem nav izpildīta, tad ir nepieciešams palielināt sijas sekcijas izmērus vai palielināt profila numuru atbilstoši sortimentu tabulām.

Iepriekš minētā siju sprieguma stāvokļa analīze liekšanā ļauj racionāli projektēt siju konstrukciju elementus, ņemot vērā to slodzes īpatnības. Tātad, piemēram, dzelzsbetona konstrukcijām ir ieteicams izmantot tērauda stiegrojumu un novietot to pa līnijām, kas sakrīt ar galveno stiepes spriegumu trajektoriju.

Ar šķērsvirziena saliekšanu stieņa šķērsgriezumā rodas ne tikai lieces moments, bet arī bīdes spēks. Līdz ar to šķērsgriezumā darbojas normāli σ un bīdes spriegumi τ. Saskaņā ar likumu par tangenciālo spriegumu savienošanu pārī, pēdējie rodas arī garengriezumos, izraisot šķiedru nobīdes viena pret otru un pārkāpjot plakano sekciju hipotēzi, kas pieņemta tīrai liecei. Rezultātā plakanas sekcijas saliecas zem slodzes. Deformāciju un spēka faktoru shēma stieņa šķērsgriezumā šķērslieces laikā. Tomēr gadījumos, kad lielākais sekcijas izmērs ir vairākas reizes mazāks par stieņa garumu, nobīdes ir nelielas un plakano posmu hipotēze tiek attiecināta uz šķērsenisko lieci. Tāpēc, izmantojot tīrās lieces formulas, tiek aprēķināti arī normālie spriegumi šķērsliecē. Bīdes spriegumi garos stieņos (l>2h) ir ievērojami mazāki nekā parastajiem. Tāpēc tie netiek ņemti vērā lieces stieņu aprēķinos, un stiprības aprēķins šķērsliecē tiek veikts tikai normāliem spriegumiem, tāpat kā tīrā liecē.

111 Sarežģīti stieņu deformāciju veidi.(bez viena attēla)

AT
Vispārīgā gadījumā gareniskās un šķērseniskās slodzes vienlaikus var iedarboties uz stieni. Ja pieņemam slīpās lieces kombināciju ar aksiālo spriegumu vai saspiešanu, tad šāda slodze noved pie lieces momentu M y un M z , šķērsspēku Q y un Q z un gareniskā spēka N parādīšanās stieņa šķērsgriezumos. sadaļā AT konsoles stienis darbosies ar šādiem spēka faktoriem: M y =F z x; Mz=Fyx; Qz =Fz; Q y = F y ; N=F x . Normālais spriegums, ko izraisa stiepes spēks F x, ir vienāds visos stieņa šķērsgriezumos un ir vienmērīgi sadalīts pa sekciju. Šo spriegumu nosaka pēc formulas: σ p =F x /A, kur A ir stieņa šķērsgriezuma laukums. Piemērojot spēku darbības neatkarības principu (ņemot vērā formulu), iegūstam šādu sakarību normālā sprieguma noteikšanai patvaļīgā punktā С: σ=N/A+M z z/J z +M z y/J z . Izmantojot šo formulu, ir iespējams noteikt maksimālo spriegumu σ max dotajā šķērsgriezumā σ max =N/A+M y /W y +M z /W z . Stiprības ticamības nosacījumam pieļaujamiem spriegumiem šajā gadījumā ir forma σ ma ≤ [σ]. Ekscentriskā spriedze (saspiešana). Ar stieņa ekscentrisku spriegojumu (saspiešanu) ārējo spēku rezultants nesakrīt ar sijas asi, bet tiek nobīdīts attiecībā pret x asi. Šis slogošanas gadījums konstrukcijas ziņā ir līdzīgs liecei ar sasprindzinājumu. Patvaļīgā stieņa šķērsgriezumā darbosies iekšējie spēka faktori: M y =Fz B ; Mz B = Fy B ; N=F, kur z B un y B ir spēka pielikšanas punkta koordinātas. Spriegumus šķērsgriezumu punktos var noteikt, izmantojot tās pašas formulas. Vīšana ar locīšanu. Daži konstrukcijas elementi darbojas vērpes un lieces apstākļos. Piemēram, zobratu vārpstas no zobiem F 1 =F 2 savienošanās spēkiem pārraida griezes momentu un lieces momentus. Rezultātā šķērsgriezumā darbosies normālie un bīdes spriegumi: σ=M y z/J y ; τ=Tρ/J p , kur M y un T ir attiecīgi lieces un griezes momenti sekcijā. (ATTĒLS NAV IEVIETOTS). Lielākie spriegumi, kas iedarbojas perifērajos punktos C un C R posmos: σ max =M y /W y ; τ max =T/W p =T/(2W y). Pamatojoties uz galvenajiem spriegumiem, izmantojot kādu no iepriekš apskatītajām stiprības teorijām, nosaka ekvivalento spriegumu. Tātad, pamatojoties uz enerģijas teoriju: σ eq =√(σ 2 max +3 τ 2 max) .

116 Bīdes, iekšējie spēki un deformācijas.(Bez iekšējiem spēka faktoriem deformācija ir kaut kāds sūds ).

NO nobīde - deformācijas veids, kad stieņa šķērsgriezumos darbojas tikai bīdes spēks, un nav citu spēka faktoru. Bīde atbilst divu vienādu, pretēji vērstu un bezgalīgi tuvu šķērsvirziena spēku iedarbībai uz stieni, izraisot griezumu pa plakni, kas atrodas starp spēkiem (kā griežot stieņus, loksnes utt. ar šķērēm). Pirms griezuma notiek deformācija - taisnā leņķa izkropļojums starp divām savstarpēji perpendikulārām līnijām. Šajā gadījumā uz izvēlētā elementa virsmām rodas bīdes spriegumi τ. Tiek saukts sprieguma stāvoklis, kurā uz atlasītā elementa virsmām rodas tikai tangenciālie spriegumi tīra maiņa. Vērtība a sauca absolūta maiņa sauc leņķi, par kādu mainās elementa taisnie leņķi relatīvā maiņa, tgγ≈γ=a/h.

Deformācija. Ja uz apaļa stieņa sānu virsmas uzliek sietu, tad pēc sagriešanas var noteikt : cirkulē cilindra ģeneratori

liela piķa spirālveida līnijās; sekcijas ir apaļas un plakanas pirms deformācijas saglabā savu formu un pēc deformācijas; notiek vienas sekcijas rotācija attiecībā pret otru noteiktā leņķī, ko sauc par vērpšanas leņķi; attālumi starp šķērsgriezumiem praktiski nemainās. Pamatojoties uz šiem novērojumiem, tiek pieņemtas hipotēzes, ka: posmi, kas ir plakani pirms vērpšanas, pēc sagriešanas paliek plakani; šķērsgriezuma rādiusi deformācijas laikā paliek taisni. Atbilstoši tam stieņa vērpes var attēlot sekciju savstarpējās griešanās radīto nobīdes rezultātā.

Mēs esam redzējuši, ka tīrā liekšanā stieņa šķērsgriezumos rodas tikai normāli spriegumi. Attiecīgie iekšējie spēki tiek samazināti līdz lieces momentam sadaļā. Šķērslieces gadījumā stieņa griezumā rodas ne tikai lieces moments, bet arī šķērsspēks, kas ir šķērsgriezuma plaknē esošo elementāru sadalīto spēku rezultants (4.23. att.). Līdz ar to šajā gadījumā šķērsgriezumos rodas ne tikai normāli, bet arī bīdes spriegumi.

Tangenciālo spriegumu rašanos pavada leņķisko deformāciju parādīšanās. Tāpēc papildus pamata nobīdēm, kas raksturīgas tīrai liecei, katrs sekcijas elementārais laukums saņem papildu leņķiskās nobīdes bīdes dēļ. Bīdes spriegumi ir nevienmērīgi sadalīti pa sekciju, tāpēc arī leņķiskās nobīdes tiks sadalītas nevienmērīgi. Tas nozīmē, ka šķērseniskās lieces gadījumā atšķirībā no tīrā izpb a šķērsgriezumi nepaliek plakani. Uz att. 4.24 parāda tipisku šķērsgriezumu izliekuma attēlu.

Tomēr šķērsgriezumu plaknes izkropļojumi normālo spriegumu vērtību būtiski neietekmē. Jo īpaši, ja šķērsspēks nemainās visā stieņa garumā, formulas (4.6) un (4.8), kas iegūtas tīras lieces gadījumā, sniegs pilnīgi precīzus rezultātus šķērseniskās lieces gadījumā. Patiešām, kad visu sekciju izliekums notiek vienādi (4.25. att.). Tāpēc ar divu blakus esošo sekciju savstarpēju rotāciju garenšķiedras AB pagarinājums būs vienāds neatkarīgi no tā, vai sekcija paliek plakana vai nē.

Ar šķērsvirziena spēku, kas mainās gar stieņa asi, tīrās lieces formulas dod zināmu kļūdu a. Veicot vienkāršu analīzi, var parādīt, ka šī kļūda ir aptuveni vienāda ar vienību, kur ir šķērsgriezuma lielums lieces plaknē; - stieņa garums. Saskaņā ar definīciju, kas sniegta § B2, stieņa raksturīga iezīme ir tā, ka tā šķērsgriezuma izmēri ir daudz mazāki par tā garumu. Līdz ar to koeficients ir salīdzinoši mazs un norādītā kļūda izrādās attiecīgi maza.

Viss iepriekš minētais dod pamatu pieņemt hipotēzi par plakaniem sekcijām. Tālāk pieņemsim, ka punktu kopa, kas veido šķērsgriezuma plakni pirms lieces, arī pēc lieces veido plakni, kas pagriezta telpā. Šis pieņēmums ir pieņemams tādā mērā, ka leņķiskās deformācijas 7 griezumā var uzskatīt par ievērojami mazākām nekā leņķiskās nobīdes izliekuma izmaiņu dēļ.

Šķērsvirziena lieces iezīme ir arī parasto spriegumu klātbūtne, kas rodas sijas garenvirziena posmos, t.i. spriegumi starp slāņiem. Šie spriegumi rodas tikai ar mainīgu šķērsvirziena spēku un ir ļoti mazi.

Tādējādi norādīto pieņēmumu ietvaros normālo spriegumu noteikšanai iegūtās formulas (4.6) un (4.8) ir piemērojamas ne tikai tīrai liecei, bet arī šķērsliecei. Tikpat piemērojama ir formula (4.5), kas dod stieņa izliekuma atkarību no lieces momenta.

Tagad noteiksim aptuveni tangenciālos spriegumus šķērsliecē. Vienkāršākais veids, kā aprēķināt šos spriegumus, ir izmantot pāra bīdes spriegumus, kas rodas stieņa gareniskajās daļās. Izvēlēsimies no stara garuma elementu (4.26. att., a). Šķērslieces gadījumā momenti, kas rodas elementa kreisajā un labajā sekcijā, nav vienādi un atšķiras gareniskajā horizontālajā griezumā, kas novilkts attālumā y no neitrālā slāņa (4.26. att., b), sadalām elementu. sadalīt divās daļās un ņemt vērā augšējās daļas līdzsvara nosacījumus. Acīmredzami normālo spēku rezultants kreisajā sadaļā iekrāsotajā zonā ir:

vai saskaņā ar formulu (4.6.),

kur atšķirībā no y apzīmē vietas pašreizējās ordinātas (sk. 4.26. att., b). Iegūtais integrālis ir statiskais moments ap x asi apgabala daļai, kas atrodas virs garengriezuma (virs līmeņa Apzīmēsim šo statisko momentu ar Tad

Labajā sadaļā parastais spēks būs atšķirīgs:

Atšķirība starp šiem spēkiem

jālīdzsvaro ar tangenciālajiem spēkiem, kas rodas elementa garengriezumā (sk. 4.26. att., b un c).

Kā pirmo tuvinājumu mēs pieņemam, ka bīdes spriegumi ir vienmērīgi sadalīti visā sekcijas platumā. Tad

Iegūto formulu sauc par Žuravska formulu pagājušā gadsimta krievu zinātnieka vārdā, kurš pirmais veica vispārēju bīdes spriegumu izpēti šķērsvirziena liekšanā.

Izteiksme (4.12) ļauj aprēķināt bīdes spriegumus, kas rodas stieņa garengriezumos. Spriegumi, kas veidojas stieņa šķērsgriezumos, ir vienādi ar tiem, kā pāri. Atkarību no y griezumā nosaka ar statisko momentu 5. Tuvojoties posma augšējai malai, tā iekrāsotās daļas laukums (sk. 4.26. att., b) samazinās līdz nullei. Tāpēc šeit, tuvojoties apakšējai malai, ēnotā daļa aptver visu posmu. Tā kā ass ir centrālā, tad arī šeit, līdz ar to bīdes spriegumi, kā izriet no formulas (4.12), griezuma augšējā un apakšējā punktā ir vienādi ar nulli.

Taisnstūra stienim ar malām un (4.27. att., a) mums ir

Sekojoši,

un tangenciālo spriegumu diagramma gar griezuma augstumu ir attēlota ar kvadrātveida parabolu. Vislielākais stress rodas plkst

Apļveida stienim (4.27. att., b), veicot vienkāršu integrācijas darbību, varat atrast

Turklāt,

Stienim, kura sekcija ir trīsstūra formā ar pamatni c un augstumu (4.27. att., c),

Maksimālais spriegums rodas attālumā no neitrālās ass:

Pēdējie divi piemēri skaidri parāda veikto darbību aptuveno raksturu. To var redzēt no tā, ka šķērsgriezumā bīdes spriegumiem ir sastāvdaļas ne tikai gar y asi, bet arī gar x asi. Patiešām, pieņemsim, kā tas tika darīts iepriekš, ka punktiem A, kas atrodas netālu no griezuma kontūras (4.28. att.), bīdes spriegums ir vērsts pa y asi. Sadalīsim vektoru divās komponentēs - pa normālu uz kontūru un pa pieskari.Atbilstoši slodzes apstākļiem stieņa ārējā virsma ir brīva no tangenciālajiem spēkiem. Tāpēc nav sprieguma pāru. Tāpēc, lai gan kopējais bīdes spriegums kontūras tuvumā ir vērsts tangenciāli kontūrai, un pieņēmums, ka tas ir vērsts pa y asi, izrādās nepareizs. Tādējādi tiek konstatēta komponentu klātbūtne gar x asi. Lai noteiktu šīs sastāvdaļas, vajadzētu izmantot sarežģītākas metodes nekā

pārskatīts iepriekš. Izmantojot elastības teorijas metodes, var parādīt, ka vairumā gadījumu komponentēm pa x asi ir ievērojami mazāka nozīme nekā pa y asi.

No iepriekš aplūkotajiem piemēriem varam izdarīt vispārīgu secinājumu, ka maksimālo bīdes spriegumu zona atrodas aptuveni sekcijas augstuma vidusdaļā un neplānsienu sekcijām tai ir kārtas vērtība.

Ir iespējams salīdzināt maksimālo normālo un maksimālo bīdes spriegumu absolūtās vērtības, kas rodas stieņa šķērsgriezumos. Piemēram, taisnstūra konsolei (4.29. att.) mums ir

Tas nozīmē, ka maksimālie bīdes spriegumi šķērsgriezumā ir saistīti ar maksimālajiem normālajiem spriegumiem aptuveni tāpat kā sekcijas augstums ir saistīts ar stieņa garumu, t.i. bīdes spriegumi ir ievērojami mazāki nekā parasti. Norādītā tāme ar dažiem izņēmumiem tiek saglabāta visiem stieņiem bez plānām sienām. Kas attiecas uz plānsienu stieņiem, tas ir īpašs jautājums.

Tā kā τmax ir mazs, stiprības aprēķins šķērsliecē tiek veikts tikai normāliem spriegumiem, tāpat kā tīrā liecē. Bīdes spriegumi netiek ņemti vērā. Tas ir jo dabiskāk, jo posma punktos, kas atrodas vistālāk no neitrālās līnijas, t.i. visbīstamākajā gadījumā bīdes spriegumi šķērsgriezumā ir nulle.

Ņemot vērā parādības kvalitatīvo pusi, jāpatur prātā, ka bīdes spriegumi šķērsgriezumos un pāri spriegumi garengriezumos, neskatoties uz to nelielību, dažos gadījumos var būtiski ietekmēt stieņa stiprības novērtējumu. Piemēram, šķērsvirzienā saliekot īsu koka siju, iznīcināšana iespējama nevis pa šķērsgriezumu iegultnē, bet gan nobīde gar garenplakni tuvu neitrālajam slānim, t.i. kur bīdes spriegumi ir maksimāli (4.30. att.).

Bīdes spriegumi garengriezumos ir esošā savienojuma izpausme starp stieņa slāņiem šķērseniskās lieces laikā. Ja šis savienojums dažos slāņos tiek pārrauts, mainās stieņa lieces raksturs. Piemēram, stienī, kas veidots no loksnēm (4.31. att., a), katra loksne liecas neatkarīgi, ja nav berzes spēku. Ārējais spēks uz loksnes ir vienāds ar un lielākais normālais spriegums loksnes šķērsgriezumā ir vienāds ar

Plakanās šķērslieces gadījumā, kad lieces moments darbojas arī sijas posmos M un bīdes spēks J, ne tikai normāli
, bet arī bīdes spriegumi .

Normālos spriegumus šķērsliecē aprēķina, izmantojot tās pašas formulas kā tīrā liecē:

;
.(6.24)

P

6.11.att. plakans līkums

Atvasinot formulu, mēs izdarīsim dažus pieņēmumus:

Bīdes spriegumi, kas darbojas vienādā attālumā plkst no neitrālās ass, nemainīga gar stara platumu;

Tangenciālie spriegumi visur ir paralēli spēkam J.

Apskatīsim konsoles siju šķērsvirziena lieces apstākļos spēka iedarbībā R. Veidosim iekšējo spēku diagrammas O y, un M z .

Uz attāluma x no sijas brīvā gala izvēlamies elementāru sijas posmu ar garumu dx un platums, kas vienāds ar sijas platumu b. Parādīsim iekšējos spēkus, kas iedarbojas uz elementa virsmām: uz virsmām cd ir šķērsspēks J y un lieces moments M z, bet uz robežas ab- arī šķērsspēks J y un lieces moments M z +dM z(jo J y paliek nemainīgs visā stara garumā un momentā M z izmaiņas, att. 6.12). Uz attāluma plkst nogriezt daļu elementa no neitrālās ass abcd, parādīsim spriegumus, kas iedarbojas uz iegūtā elementa skaldnēm mbcn, un apsveriet tā līdzsvaru. Uz virsmām, kas ir daļa no sijas ārējās virsmas, nav sprieguma. Elementa sānu virsmās no lieces momenta darbības M z, rodas normāls stress:

; (6.25)

. (6.26)

Turklāt uz šīm sejām no šķērsvirziena spēka iedarbības J y, rodas bīdes spriegumi , tie paši spriegumi rodas saskaņā ar likumu par tangenciālo spriegumu savienošanu elementa augšējā virsmā.

Sastādām elementa līdzsvara vienādojumu mbcn, projicējot aplūkojamos izrietošos spriegumus uz asi x:

. (6.29)

Izteiksme zem integrālās zīmes ir elementa sānu virsmas statiskais moments mbcn par asi x, lai mēs varētu rakstīt

. (6.30)

Ņemot vērā, ka saskaņā ar D. I. Žuravska diferenciālajām atkarībām, liecoties,

, (6.31)

izteiciens priekš pieskares spriegumus šķērseniskās lieces laikā var pārrakstīt šādi ( Žuravska formula)

. (6.32)

Analizēsim Žuravska formulu.

J y ir šķērsspēks aplūkotajā griezumā;

Dž z - sekcijas aksiālais inerces moments ap asi z;

b- sekcijas platums bīdes spriegumu noteikšanas vietā;

ir statiskais moments ap z-asi sekcijas daļai, kas atrodas virs (vai zem) šķiedras un kurā nosaka bīdes spriegumu:

, (6.33)

kur un F" - attiecīgi smaguma centra un attiecīgās sekcijas daļas laukuma koordinātas.

6.6. Pabeigt stiprības pārbaudi. Bīstami posmi un bīstamie punkti

Lai pārbaudītu lieces stiprību, atbilstoši ārējām slodzēm, kas iedarbojas uz siju, tiek veidoti iekšējo spēku izmaiņu diagrammi visā tās garumā un tiek noteikti sijas bīstamie posmi, kuriem katram jāveic stiprības pārbaude. .

Ar pilnu stiprības pārbaudi būs vismaz trīs šādas sadaļas (dažreiz tās sakrīt):

Sadaļa, kurā lieces moments M z sasniedz maksimālo modulo vērtību;

Sadaļa, kurā šķērsvirziena spēks J y, sasniedz maksimālo modulo vērtību;

Sadaļa, kurā un lieces moments M z un bīdes spēks J y sasniegt pietiekami lielas moduļa vērtības.

Katrā no bīstamajiem posmiem, izveidojot normālo un bīdes spriegumu diagrammas, ir jāatrod posma bīstamie punkti (katram no tiem tiek veikta stiprības pārbaude), kas arī būs vismaz trīs:

Punkts, kurā tiek radīts normāls stress , sasniedz to maksimālo vērtību, - tas ir, punkts uz sijas ārējās virsmas atrodas vistālāk no sekcijas neitrālās ass;

Punkts, kurā rodas bīdes spriegumi sasniedz maksimālo vērtību, - punkts, kas atrodas uz posma neitrālās ass;

Punkts, kurā gan normālie spriegumi, gan bīdes spriegumi sasniedz pietiekami lielas vērtības (šī pārbaude ir jēga tādām sekcijām kā tee vai I-siju, kur sekcijas platums nav nemainīgs augstumā).