Kõverjoonelise trapetsi arvutamine. Kõverajoonelise trapetsi pindala
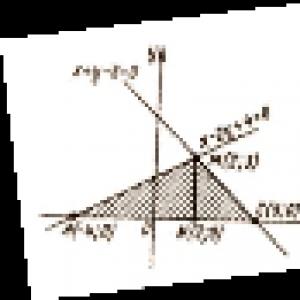
Näide1 . Arvutage joonise pindala, mis on piiratud joontega: x + 2y - 4 = 0, y = 0, x = -3 ja x = 2
Ehitame joonise (vt joonis.) Ehitame sirge x + 2y - 4 \u003d 0 mööda kahte punkti A (4; 0) ja B (0; 2). Väljendades y-d x-iga, saame y \u003d -0,5x + 2. Vastavalt valemile (1), kus f (x) \u003d -0,5x + 2, a \u003d -3, b \u003d 2, me leida
S \u003d \u003d [-0,25 \u003d 11,25 ruutmeetrit ühikut
Näide 2 Arvutage joontega piiratud joonise pindala: x - 2y + 4 \u003d 0, x + y - 5 \u003d 0 ja y \u003d 0.
Lahendus. Ehitame figuuri.
Ehitame sirge x - 2y + 4 = 0: y = 0, x = - 4, A (-4; 0); x = 0, y = 2, B(0; 2).
Ehitame sirge x + y - 5 = 0: y = 0, x = 5, С(5; 0), x = 0, y = 5, D(0; 5).
Leidke sirgete lõikepunkt, lahendades võrrandisüsteemi:
x = 2, y = 3; M(2; 3).
Vajaliku pindala arvutamiseks jagame AMC kolmnurga kaheks kolmnurgaks AMN ja NMC, kuna kui x muutub A-st N-ks, on pindala piiratud sirgjoonega ja kui x muutub N-st C-ks, on see sirgjoon.
Kolmnurga AMN jaoks on meil: ; y = 0,5x + 2, st f (x) = 0,5x + 2, a = 4, b = 2.
NMC kolmnurga jaoks on meil: y = - x + 5, st f(x) = - x + 5, a = 2, b = 5.
Arvutades iga kolmnurga pindala ja liites tulemused, leiame:
ruut ühikut
ruut ühikut
9 + 4, 5 = 13,5 ruutmeetrit ühikut Kontrollige: = 0,5AC = 0,5 ruutmeetrit. ühikut
Näide 3 Arvutage joontega piiratud kujundi pindala: y = x 2 , y=0, x=2, x=3.
Sel juhul on vaja arvutada kõverjoonelise trapetsi pindala, mis on piiratud parabooliga y = x 2 , sirgjooned x \u003d 2 ja x \u003d 3 ning Ox telg (vt joonis.) Vastavalt valemile (1) leiame kõverjoonelise trapetsi pindala
= = 6kv. ühikut
Näide 4 Arvutage joontega piiratud joonise pindala: y \u003d - x 2 + 4 ja y = 0
Ehitame figuuri. Soovitud ala on ümbritsetud parabooli y \u003d - x vahele 2 + 4 ja telg Oh.
Leidke parabooli ja x-telje lõikepunktid. Eeldades y \u003d 0, leiame x \u003d Kuna see joonis on Oy telje suhtes sümmeetriline, arvutame Oy teljest paremal asuva joonise pindala ja kahekordistame tulemuse: \u003d + 4x] ruutmeetrit ühikut 2 = 2 ruutmeetrit ühikut
Näide 5 Arvutage joontega piiratud kujundi pindala: y 2 = x, yx = 1, x = 4
Siin on vaja arvutada kõverjoonelise trapetsi pindala, mis on piiratud parabooli y ülemise haruga 2 \u003d x, härja telg ja sirgjooned x \u003d 1x \u003d 4 (vt joonis)
Vastavalt valemile (1), kus f(x) = a = 1 ja b = 4, on meil = (= ruutühikud
Näide 6 . Arvutage joonise pindala, mis on piiratud joontega: y = sinx, y = 0, x = 0, x = .
Soovitud ala on piiratud poollaine sinusoidi ja Ox-teljega (vt joonis).
Meil on - cosx \u003d - cos \u003d 1 + 1 \u003d 2 ruutmeetrit. ühikut
Näide 7 Arvutage joonise pindala, mis on piiratud joontega: y \u003d - 6x, y \u003d 0 ja x \u003d 4.
Joonis asub Ox-telje all (vt joonis).
Seetõttu leitakse selle pindala valemiga (3)
= =
Näide 8 Arvutage joonise pindala, mis on piiratud joontega: y \u003d ja x \u003d 2. Koostame punktide kaupa kõvera y \u003d (vt joonist). Seega leitakse joonise pindala valemiga (4)
Näide 9 .
X 2 + y 2 = r 2 .
Siin peate arvutama ala, mis on piiratud ringiga x 2 + y 2 = r 2 st ringi pindala raadiusega r, mille keskpunkt on alguspunktis. Leiame selle ala neljanda osa, võttes integratsiooni piirid 0-st
dor; meil on: 1 = = [
Seega 1 =
Näide 10 Arvutage joontega piiratud joonise pindala: y \u003d x 2 ja y = 2x
Seda arvu piirab parabool y \u003d x 2 ja sirge y \u003d 2x (vt joonis.) Antud sirgete lõikepunktide määramiseks lahendame võrrandisüsteemi: x 2 – 2x = 0 x = 0 ja x = 2
Kasutades ala leidmiseks valemit (5), saame
= funktsioonigraafik y = x 2 + 2 asuvad üle teljeHÄRG, Sellepärast:
Vastus: .
Kellel on raskusi kindla integraali arvutamisega ja Newtoni-Leibnizi valemi rakendamisega
,
viidata loengule Kindel integraal. Lahendusnäited. Pärast ülesande täitmist on alati kasulik vaadata joonist ja aru saada, kas vastus on tõeline. Sel juhul loendame "silma järgi" joonisel olevate lahtrite arvu - noh, umbes 9 trükitakse, see näib olevat tõsi. On täiesti selge, et kui meil oleks, ütleme, vastus: 20 ruutühikut, siis ilmselgelt tehti kuskil viga - 20 lahtrit ilmselt ei mahu kõnealusele joonisele, kõige rohkem kümmekond. Kui vastus osutus eitavaks, siis oli ka ülesanne valesti lahendatud.
Näide 2
Arvutage joontega piiratud kujundi pindala xy = 4, x = 2, x= 4 ja telg HÄRG.
See on tee-seda-ise näide. Täislahendus ja vastus tunni lõpus.
Mida teha, kui kõverjooneline trapets asub telje allHÄRG?
Näide 3
Arvutage joontega piiratud kujundi pindala y = e-x, x= 1 ja koordinaatteljed.
Lahendus: teeme joonise:
Kui kõverjooneline trapets täiesti silla all HÄRG , siis selle pindala saab leida valemiga:
Sel juhul:
.
Tähelepanu! Kahte tüüpi ülesandeid ei tohiks segi ajada:
1) Kui teil palutakse lahendada ainult kindel integraal ilma geomeetrilise tähenduseta, võib see olla negatiivne.
2) Kui teil palutakse leida figuuri pindala kindla integraali abil, siis on pindala alati positiivne! Seetõttu ilmub just vaadeldavas valemis miinus.
Praktikas paikneb joonis enamasti nii ülemisel kui alumisel pooltasandil ja seetõttu liigume lihtsamate kooliülesannete juurest edasi sisukamate näidete juurde.
Näide 4
Leidke joontega piiratud tasapinnalise kujundi pindala y = 2x – x 2 , y = -x.
Lahendus: Kõigepealt peate tegema joonise. Piirkonnaülesannetes joonise konstrueerimisel huvitavad meid enim sirgete lõikepunktid. Leidke parabooli lõikepunktid y = 2x – x 2 ja sirge y = -x. Seda saab teha kahel viisil. Esimene viis on analüütiline. Lahendame võrrandi:
Seega integratsiooni alumine piir a= 0, integreerimise ülempiir b= 3. Tihti on tulusam ja kiirem joonte konstrueerimine punkt-punkti haaval, samas kui lõimimise piirid selgitatakse välja justkui “iseenesest”. Sellegipoolest tuleb piiride leidmise analüütilist meetodit mõnikord siiski kasutada, kui näiteks graafik on piisavalt suur või keermestatud konstruktsioon ei toonud esile integreerimise piire (need võivad olla murdosalised või irratsionaalsed). Pöördume tagasi oma ülesande juurde: ratsionaalsem on kõigepealt konstrueerida sirge ja alles seejärel parabool. Teeme joonise:
Kordame, et punktkonstruktsioonis selgitatakse integratsiooni piirid kõige sagedamini välja “automaatselt”.
Ja nüüd töövalem:
Kui segmendil [ a; b] mingi pidev funktsioon f(x) suurem või võrdne mingi pidev funktsioon g(x), siis saab vastava joonise pindala leida valemiga:
Siin pole enam vaja mõelda, kus kujund asub - telje kohal või telje all, vaid on oluline, milline diagramm on ÜLAL(teise graafiku suhtes), ja milline neist on ALL.
Vaadeldavas näites on ilmne, et lõigul asub parabool sirge kohal ja seetõttu alates 2. x – x 2 tuleb lahutada - x.
Lahenduse valmimine võib välja näha järgmine:
Soovitud figuuri piirab parabool y = 2x – x 2 ülemine ja sirge y = -x altpoolt.
Segmendis 2 x – x 2 ≥ -x. Vastavalt vastavale valemile:
Vastus: .
Tegelikult on alumise pooltasandi kõverjoonelise trapetsi pindala koolivalem (vt näide nr 3) valemi erijuhtum
.
Kuna telg HÄRG on antud võrrandiga y= 0 ja funktsiooni graafik g(x) asub telje all HÄRG, See
.
Ja nüüd paar näidet iseseisvaks otsuseks
Näide 5
Näide 6
Leidke joontega piiratud kujundi pindala
Pindala arvutamise ülesannete lahendamise käigus teatud integraali abil juhtub mõnikord naljakas juhtum. Joonis tehti õigesti, arvutused olid õiged, kuid tähelepanematuse tõttu ... leidis vale kujundi ala.
Näide 7
Kõigepealt joonistame:
Joonis, mille ala peame leidma, on varjutatud sinisega.(vaadake hoolikalt seisukorda - kuidas figuur on piiratud!). Kuid praktikas otsustavad nad tähelepanematuse tõttu sageli, et peavad leidma roheliseks varjutatud figuuri ala!
See näide on kasulik ka selle poolest, et selles arvutatakse joonise pindala kahe kindla integraali abil. Tõesti:
1) Lõigul [-1; 1] telje kohal HÄRG graafik on sirge y = x+1;
2) Segmendil telje kohal HÄRG hüperbooli graafik asub y = (2/x).
On üsna ilmne, et piirkondi saab (ja tuleks) lisada, seega:
Vastus:
Näide 8
Arvutage joontega piiratud kujundi pindala
Esitame võrrandid "kooli" kujul
ja joonistage joon:
Jooniselt on näha, et meie ülempiir on “hea”: b = 1.
Aga mis on alumine piir? On selge, et see pole täisarv, aga mis?
Võib olla, a=(-1/3)? Aga kus on garantii, et joonis on tehtud täiusliku täpsusega, see võib ka selguda a=(-1/4). Mis siis, kui me ei saanud graafikust üldse õiget?
Sellistel juhtudel tuleb kulutada lisaaega ja integreerimise piire analüütiliselt täpsustada.
Leia graafikute lõikepunktid
Selleks lahendame võrrandi:
.
Seega a=(-1/3).
Edasine lahendus on triviaalne. Peaasi, et vahetustes ja märkides segadusse ei läheks. Siin pole arvutused just kõige lihtsamad. Segmendil
, 
,
vastavalt vastavale valemile:
Vastus: 
Tunni kokkuvõttes käsitleme kaht ülesannet raskemaks.
Näide 9
Arvutage joontega piiratud kujundi pindala
Lahendus: joonistage see joonis joonisele.
Punkthaaval joonise joonistamiseks peate teadma sinusoidi välimust. Üldiselt on kasulik teada kõigi elementaarfunktsioonide graafikuid, aga ka mõningaid siinuse väärtusi. Need leiate väärtuste tabelist trigonomeetrilised funktsioonid. Mõnel juhul (näiteks antud juhul) on lubatud konstrueerida skemaatiline joonis, millel tuleb põhimõtteliselt õigesti kuvada graafikud ja integreerimispiirid.
Integratsioonipiirangutega siin probleeme pole, need tulenevad otse tingimusest:
- "x" muutub nullist "pi". Teeme järgmise otsuse:
Segmendil funktsiooni graafik y= patt 3 x asub telje kohal HÄRG, Sellepärast:
(1) Näete, kuidas siinused ja koosinused on tunnis paarituteks astmeteks integreeritud Trigonomeetriliste funktsioonide integraalid. Näpistame ühe siinuse ära.
(2) Kasutame vormis trigonomeetrilist põhiidentiteeti
(3) Muudame muutujat t= cos x, siis: asub telje kohal, seega:
.
.
Märge: pane tähele kuidas võetakse kuubis puutuja integraal, siin kasutatakse trigonomeetrilise põhiidentiteedi tagajärge
.
Sisestage funktsioon, mille integraali soovite leida
Kalkulaator pakub kindlate integraalide DETAILNE lahendust.
See kalkulaator lahendab funktsiooni f(x) kindla integraali antud ülemise ja alumise piiriga.
Näited
Kraadi kasutamisega
(ruut ja kuubik) ja murrud
(x^2 - 1)/(x^3 + 1)
Ruutjuur
ruut(x)/(x + 1)
kuupjuur
Cbrt(x)/(3*x + 2)
Siinuse ja koosinuse kasutamine
2*sin(x)*cos(x)
Arcsine
X*artsin(x)
Kaarkoosinus
x*arccos(x)
Logaritmi rakendamine
X*log(x, 10)
naturaallogaritm
Eksponent
Tg(x)*sin(x)
Kotangent
Ctg(x)*cos(x)
Irratsionaalsed murded
(ruut(x) - 1) / ruut (x^2 - x - 1)
Arktangent
X*arctg(x)
Kaare puutuja
X*arсctg(x)
Hüberboolne siinus ja koosinus
2*sh(x)*ch(x)
Hüberboolne puutuja ja kotangent
ctgh(x)/tgh(x)
Hüberboolne arkosiin ja arkosiin
X^2*arcsinh(x)*arccosh(x)
Hüberboolne arkotangens ja arkotangens
X^2*arctgh(x)*arctgh(x)
Avaldiste ja funktsioonide sisestamise reeglid
Avaldised võivad koosneda funktsioonidest (tähistused on antud tähestikulises järjekorras): absoluutne (x) Absoluutne väärtus x
(moodul x või |x|)
arccos (x) Funktsioon - kaarekoosinus x arccosh(x) Kaarkoosinus hüperboolne alates x arcsin(x) Arcsine alates x arcsinh(x) Arksiin hüperboolne alates x arctg(x) Funktsioon – kaartangens alates x arctgh(x) Kaartangens on hüperboolne alates x e e arv, mis on ligikaudu võrdne 2,7-ga exp(x) Funktsioon – astendaja alates x(mis on e^x)
log(x) või log(x) naturaalne logaritm x
(Et saada log7(x), peate sisestama log(x)/log(7) (või näiteks jaoks log10(x)=log(x)/log(10)) pi Arv on "Pi", mis on ligikaudu võrdne 3,14-ga sin(x) Funktsioon – siinus x cos(x) Funktsioon – koosinus x sinh(x) Funktsioon – hüperboolne siinus x sularaha (x) Funktsioon – hüperboolne koosinus x sqrt(x) Funktsioon on ruutjuur x sqr(x) või x^2 Funktsioon – ruut x tg(x) Funktsioon – puutuja alates x tgh(x) Funktsioon – hüperboolne tangens x cbrt(x) Funktsioon on kuupjuur x
Avaldistes saate kasutada järgmisi toiminguid: Reaalarvud sisestage vormi 7.5
, Mitte 7,5
2*x- korrutamine 3/x- jagunemine x^3- astendamine x + 7- lisamine x - 6- lahutamine
Teised omadused: korrus (x) Funktsioon - ümardamine x alla (näide korrus(4,5)==4,0) lagi (x) Funktsioon - ümardamine xüles (näide lagi(4,5)==5,0) märk (x) Funktsioon – märk x erf(x) Veafunktsioon (või tõenäosusintegraal) Laplace (x) Laplace'i funktsioon
Sellest artiklist saate teada, kuidas integraalarvutuste abil leida joontega piiratud joonise pindala. Esimest korda puutume sellise probleemi sõnastamisega kokku keskkoolis, kui teatud integraalide õpe on just lõppenud ja on aeg alustada praktikas saadud teadmiste geomeetrilist tõlgendamist.
Niisiis, mida on vaja integraalide abil joonise pindala leidmise probleemi edukaks lahendamiseks:
- Oskus õigesti joonistada jooniseid;
- Oskus lahendada kindlat integraali, kasutades tuntud Newton-Leibnizi valemit;
- Võimalus "näha" tulusamat lahendust - s.t. aru saada, kuidas sel või teisel juhul on integreerimist mugavam läbi viia? Piki x-telge (OX) või y-telge (OY)?
- Noh, kus ilma õigete arvutusteta?) See hõlmab mõistmist, kuidas seda teist tüüpi integraale lahendada, ja õigeid arvulisi arvutusi.
Algoritm joontega piiratud joonise pindala arvutamise ülesande lahendamiseks:
1. Ehitame joonise. Soovitav on seda teha paberil puuris, suures mahus. Kirjutame iga graafiku kohale pliiatsiga selle funktsiooni nime. Graafikutele allkiri tehakse ainult edasiste arvutuste hõlbustamiseks. Pärast soovitud joonise graafiku saamist on enamikul juhtudel kohe selge, milliseid integreerimispiiranguid kasutatakse. Seega lahendame probleemi graafiliselt. Siiski juhtub, et piiride väärtused on murdosa või irratsionaalsed. Seetõttu saate teha täiendavaid arvutusi, minge teise sammu juurde.
2. Kui integreerimispiirid pole selgesõnaliselt paika pandud, siis leiame graafikute lõikepunktid omavahel ja vaatame, kas meie graafiline lahendus ühtib analüütilise lahendusega.
3. Järgmisena peate joonist analüüsima. Sõltuvalt sellest, kuidas funktsioonide graafikud asuvad, on joonise pindala leidmiseks erinevad lähenemisviisid. Mõelge erinevatele näidetele joonise pindala leidmiseks integraalide abil.
3.1. Probleemi kõige klassikalisem ja lihtsam versioon on siis, kui peate leidma kõverjoonelise trapetsi pindala. Mis on kõverjooneline trapets? See on tasane kujund, mis on piiratud x-teljega (y=0), sirge x = a, x = b ja mis tahes pidev kõver intervallil alates a enne b. Samal ajal on see näitaja mittenegatiivne ja ei asu x-teljelt madalamal. Sel juhul on kõverjoonelise trapetsi pindala arvuliselt võrdne Newtoni-Leibnizi valemi abil arvutatud kindla integraaliga:
Näide 1 y = x2 - 3x + 3, x = 1, x = 3, y = 0.
Millised jooned määratlevad figuuri? Meil on parabool y = x2 - 3x + 3, mis asub telje kohal Oh, see ei ole negatiivne, sest kõik selle parabooli punktid on positiivsed. Järgmiseks antud sirgjooned x = 1 Ja x = 3 mis kulgevad paralleelselt teljega OU, on joonise piirjooned vasakul ja paremal. Noh y = 0, ta on x-telg, mis piirab joonist altpoolt. Saadud joonis on varjutatud, nagu on näha vasakpoolsel joonisel. Sel juhul saate kohe alustada probleemi lahendamisega. Meie ees on lihtne näide kõverjoonelisest trapetsist, mille lahendame seejärel Newtoni-Leibnizi valemi abil.
3.2. Eelmises punktis 3.1 analüüsiti juhtumit, kui kõverjooneline trapets paikneb x-telje kohal. Mõelge nüüd juhtumile, kui ülesande tingimused on samad, välja arvatud see, et funktsioon asub x-telje all. Standardsele Newtoni-Leibnizi valemile lisatakse miinus. Kuidas sellist probleemi lahendada, kaalume edasi.
Näide 2 . Arvutage joontega piiratud kujundi pindala y=x2+6x+2, x=-4, x=-1, y=0.
Selles näites on meil parabool y=x2+6x+2, mis pärineb telje alt Oh, sirge x = -4, x = -1, y = 0. Siin y = 0 piirab soovitud figuuri ülalt. Otsene x = -4 Ja x = -1 need on piirid, mille piires arvutatakse kindel integraal. Joonise pindala leidmise probleemi lahendamise põhimõte langeb peaaegu täielikult kokku näitega number 1. Ainus erinevus on see, et antud funktsioon ei ole positiivne ja on ka intervallil pidev. [-4; -1] . Mida ei tähenda positiivne? Nagu jooniselt näha, on antud x-i piires oleval joonisel eranditult "negatiivsed" koordinaadid, mida peame ülesande lahendamisel nägema ja meeles pidama. Figuuri pindala otsime Newton-Leibnizi valemi abil, ainult alguses miinusmärgiga.
Artikkel ei ole lõpetatud.
Arvutage joontega piiratud kujundi pindala.
Lahendus.
Leiame etteantud sirgete lõikepunktid. Selleks lahendame võrrandisüsteemi:
Antud sirgete lõikepunktide abstsisside leidmiseks lahendame võrrandi:
Leiame: x 1 = -2, x 2 = 4.
Niisiis, need sirged, mis on parabool ja sirgjoon, ristuvad punktides A(-2; 0), B(4; 6).
Need jooned moodustavad suletud joonise, mille pindala arvutatakse ülaltoodud valemi abil:
Newtoni-Leibnizi valemi järgi leiame:
Leidke ellipsiga piiratud ala pindala.
Lahendus.
I kvadrandi ellipsi võrrandist saame . Siit saame valemi järgi
Rakendame asendust x = a patt t, dx = a cos t dt. Uued integratsiooni piirid t = α Ja t = β määratakse võrranditest 0 = a patt t, a = a patt t. Saab panna α = 0 ja β = π /2.
Leiame neljandiku vajalikust pinnast
Siit S = pab.
Leidke joontega piiratud kujundi pindalay = - x 2 + x + 4 jay = - x + 1.
Lahendus.
Leidke sirgete lõikepunktid y = -x 2 + x + 4, y = -x+ 1, võrdsustades joonte ordinaate: - x 2 + x + 4 = -x+ 1 või x 2 - 2x- 3 = 0. Leia juured x 1 = -1, x 2 = 3 ja neile vastavad ordinaadid y 1 = 2, y 2 = -2.
Kasutades joonise pindala valemit, saame
Leidke parabooliga ümbritsetud alay = x 2 + 1 ja otsenex + y = 3.
Lahendus.
Võrrandisüsteemi lahendamine
leida ristumispunktide abstsissid x 1 = -2 ja x 2 = 1.
Eeldusel y 2 = 3 - x Ja y 1 = x 2 + 1, saadud valemi põhjal
Arvutage Bernoulli lemniskaadi pindalar 2 = a 2 cos 2 φ .
Lahendus.
Polaarkoordinaatide süsteemis on joonise pindala, mis on piiratud kõvera kaarega r = f(φ ) ja kaks polaarraadiust φ 1 = ʅ Ja φ 2 = ʆ , väljendatakse integraaliga
Kõvera sümmeetria tõttu määrame kõigepealt ühe neljandiku soovitud pindalast
Seega on kogupindala S = a 2 .
Arvutage astroidi kaare pikkusx 2/3 + y 2/3 = a 2/3 .
Lahendus.
Kirjutame astroidi võrrandi kujule
(x 1/3) 2 + (y 1/3) 2 = (a 1/3) 2 .
Paneme x 1/3 = a 1/3 kulu t, y 1/3 = a 1/3 patt t.
Siit saame astroidi parameetrilised võrrandid
x = a cos 3 t, y = a patt 3 t, (*)
kus 0 ≤ t ≤ 2π .
Kõvera (*) sümmeetriat silmas pidades piisab, kui leida neljandiku kaare pikkusest L parameetri muutusele vastav t 0 kuni π /2.
Saame
dx = -3a cos 2 t patt t dt, dy = 3a patt 2 t cos t dt.
Siit leiame
Saadud avaldise integreerimine vahemikus 0 kuni π /2, saame
Siit L = 6a.
Leidke Archimedese spiraaliga piiratud alar = aφ ja kaks raadiusvektorit, mis vastavad polaarnurkadeleφ 1 Jaφ 2 (φ 1 < φ 2 ).
Lahendus.
Kõveraga piiratud ala r = f(φ ) arvutatakse valemiga , kus α Ja β - polaarnurga muutumise piirid.
Seega saame
(*)
Alates (*) järeldub, et ala, mis on piiratud polaartelje ja Archimedese spiraali esimese pöördega ( φ 1 = 0; φ 2 = 2π ):
Samamoodi leiame ala, mis on piiratud polaartelje ja Archimedese spiraali teise pöördega ( φ 1 = 2π ; φ 2 = 4π ):
Nõutav pindala on võrdne nende alade erinevusega
Arvutage ümber telje pöörlemisel saadud keha ruumalaOx paraboolidega piiratud kujundy = x 2 Jax = y 2 .
Lahendus.
Lahendame võrrandisüsteemi
ja saada x 1 = 0, x 2 = 1, y 1 = 0, y 2 = 1, kust kõverate lõikepunktid O(0; 0), B(üksteist). Nagu jooniselt näha, on pöördekeha soovitud ruumala võrdne ümber telje pöörlemisel tekkinud kahe ruumala vahega Ox kõverjoonelised trapetsid OCBA Ja ODBA:
Arvutage teljega piiratud pindalaOx ja sinusoidy = pattx segmentide kohta: a); b) .
Lahendus.
a) Lõigul funktsioon sin x säilitab märgi ja seega valemiga , eeldades y= patt x, leiame
b) Lõigul funktsioon sin x muudab märki. Ülesande õigeks lahendamiseks on vaja segment jagada kaheks ja [ π , 2π ], millest igaühes säilitab funktsioon oma märgi.
Vastavalt märkide reeglile on lõigul [ π , 2π ] ala on võetud miinusmärgiga.
Selle tulemusena on soovitud ala võrdne
Määrake ellipsi pöörlemisel saadud pinnaga piiratud keha ruumalaümber suurteljea .
Lahendus.
Arvestades, et ellips on sümmeetriline koordinaattelgede suhtes, piisab, kui leida ümber telje pöörlemisel tekkiva ruumala Ox ala OAB, võrdub ühe neljandikuga ellipsi pindalast ja kahekordistage tulemus.
Tähistagem läbi pöördekeha mahtu V x; siis on meil valemi põhjal , kus 0 ja a- punktide abstsissid B Ja A. Ellipsi võrrandist leiame . Siit
Seega on nõutav maht võrdne . (Kui ellips pöörleb ümber väiketelje b, keha maht on )
Leidke paraboolidega piiratud alay 2 = 2 px Jax 2 = 2 py .
Lahendus.
Esiteks leiame paraboolide lõikepunktide koordinaadid, et määrata integreerimisintervall. Algseid võrrandeid teisendades saame ja . Võrdsustades need väärtused, saame või x 4 - 8lk 3 x = 0.
x 4 - 8lk 3 x = x(x 3 - 8lk 3) = x(x - 2lk)(x 2 + 2px + 4lk 2) = 0.
Leiame võrrandite juured:
Arvestades asjaolu, et punkt A paraboolide ristumiskoht on esimesel veerandil, siis lõimumise piirid x= 0 ja x = 2lk.
Soovitud ala leitakse valemiga
