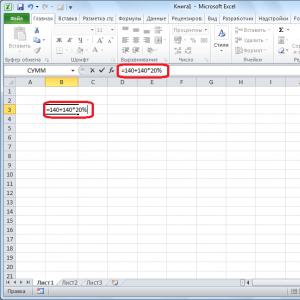
Formula segmenta viduspunkta koordinātu atrašanai. Kā atrast līnijas viduspunkta koordinātas

Sākotnējā ģeometriskā informācija

Segmenta jēdziens, tāpat kā punkta, līnijas, stara un leņķa jēdziens, attiecas uz sākotnējo ģeometrisko informāciju. Ģeometrijas izpēte sākas ar šiem jēdzieniem.

Ar “sākotnējo informāciju” parasti saprot kaut ko elementāru un vienkāršu. Saprotot, iespējams, tas tā ir. Tomēr šādus vienkāršus jēdzienus bieži atrod un izrādās, ka tie nepieciešami ne tikai mūsu ikdienas dzīvē, bet arī ražošanā, celtniecībā un citās mūsu dzīves sfērās.

Sāksim ar definīcijām.

1. definīcija

Segments ir taisnas līnijas daļa, ko ierobežo divi punkti (gali).

Ja segmenta galos ir punkti $ A $ un $ B $, tad izveidoto segmentu raksta kā $ AB $ vai $ BA $. Šajā segmentā ir punkti $ A $ un $ B $, kā arī visi taisnās līnijas punkti, kas atrodas starp šiem punktiem.

2. definīcija

Segmenta viduspunkts ir segmenta punkts, kas to sadala uz pusēm divos vienādos segmentos.

Ja tas ir punkts $ C $, tad $ AC \u003d CB $.

Segmenta mērīšanu veic, salīdzinot ar noteiktu segmentu, kas ņemts par mērvienību. Visbiežāk izmanto centimetru. Ja konkrētajā segmentā centimetrs tiek sakrauts precīzi četras reizes, tad tas nozīmē, ka šī segmenta garums ir USD 4 $ cm.

Iepazīstināsim ar vienkāršu novērojumu. Ja punkts sadala segmentu divos segmentos, tad visa segmenta garums ir vienāds ar šo segmentu garumu summu.

Formula segmenta viduspunkta koordinātu atrašanai

Līnijas segmenta viduspunkta koordinātu atrašanas formula attiecas uz analītiskās ģeometrijas gaitu plaknē.

Definēsim koordinātas.

3. definīcija

Koordinātas ir definēti (vai pasūtīti) skaitļi, kas norāda punkta atrašanās vietu plaknē, virsmā vai telpā.

Mūsu gadījumā koordinātas tiek iezīmētas plaknē, ko nosaka koordinātu asis.

3. attēls. Koordinātu plakne. Autors24 - studentu darbu apmaiņa tiešsaistē

Aprakstīsim attēlu. Plaknē tiek izvēlēts punkts, ko sauc par sākumu. To apzīmē ar burtu $ O $. Caur koordinātu sākumu tiek novilktas divas taisnas līnijas (koordinātu asis), kas krustojas taisnā leņķī, un viena no tām ir stingri horizontāla, bet otra - vertikāla. Šī situācija tiek uzskatīta par izplatītu. Horizontālo līniju sauc par abscisas asi un apzīmē ar $ OX $, vertikālo līniju sauc par $ OY $ ordinātu asi.

Tādējādi asis nosaka $ XOY $ plakni.

Punktu koordinātas šādā sistēmā nosaka ar diviem cipariem.

Ir dažādas formulas (vienādojumi), kas nosaka noteiktas koordinātas. Parasti analītiskās ģeometrijas laikā tiek pētītas dažādas līniju, leņķu, segmentu garumu un citu formulas.

Dosimies tieši uz segmenta viduspunkta koordinātu formulu.

4. definīcija

Ja punkta $ E (x, y) $ koordinātas ir segmenta $ M_1M_2 $ viduspunkts, tad:

4. attēls. Segmenta viduspunkta koordinātu atrašanas formula. Autors24 - studentu darbu apmaiņa tiešsaistē

Praktiskā daļa

Skolas ģeometrijas kursa piemēri ir diezgan vienkārši. Apsvērsim vairākus galvenos.

Lai labāk saprastu, vispirms apskatīsim elementāru vizuālo piemēru.

1. piemērs

Mums ir zīmējums:

Attēlā segmenti $ AC, CD, DE, EB $ ir vienādi.

1. Kādi ir D D $ viduspunkti?
2. Kur ir USD DB $ segmenta viduspunkts?

1. punkts $ D $ ir segmentu $ AB $ un $ CE $ viduspunkts;
2. punkts $ E $.

Apskatīsim vēl vienu vienkāršu piemēru, kur jums jāaprēķina garums.

2. piemērs

Punkts $ B $ ir segmenta $ AC $ viduspunkts. $ AB \u003d 9 $ cm. Cik garš ir $ AC $?

Tā kā m. $ B $ dala $ AC $ uz pusēm, tad $ AB \u003d BC \u003d 9 $ redzēt. Tādējādi $ AC \u003d 9 + 9 \u003d 18 $ redzēt.

Atbilde: 18 cm.

Citi līdzīgi piemēri parasti ir identiski un koncentrējas uz spēju salīdzināt garuma vērtības un to attēlojumu ar algebriskām darbībām. Bieži vien uzdevumos ir gadījumi, kad centimetrs segmentā neatbilst pāra reižu skaitam. Tad mērvienību sadala vienādās daļās. Mūsu gadījumā centimetru dala ar 10 milimetriem. Atlikušo daļu mēra atsevišķi, salīdzinot ar milimetru. Sniegsim piemēru, lai parādītu šādu gadījumu.

Pēc rūpīga darba es pēkšņi pamanīju, ka tīmekļa lapu izmēri ir pietiekami lieli, un, ja tas notiek šādi, tad jūs mierīgi un mierīgi varat kļūt brutāli \u003d) Tāpēc es jūsu uzmanībai pievērsu nelielu eseju, kas veltīta ļoti izplatītai ģeometriskai problēmai - par segmenta sadalīšanu šajā ziņāun kā īpašs gadījums par segmenta sadalīšanu uz pusēm.

Šis uzdevums viena vai otra iemesla dēļ nederēja citās stundās, bet tagad ir lieliska iespēja to izskatīt sīkāk un lēnām. Labā ziņa ir tā, ka mēs nedaudz atcelsimies no vektoriem un koncentrēsimies uz punktiem un līnijām.

Līniju dalīšanas formulas šajā ziņā

Šajā ziņā segmenta dalīšanas jēdziens

Bieži vien nav jāgaida solītais, mēs tūlīt apsvērsim dažus punktus un, kas acīmredzami neticami, - segmentu:

Apsvērtā problēma attiecas gan uz plaknes segmentiem, gan uz kosmosa segmentiem. Tas ir, demonstrācijas segmentu var izvietot lidmašīnā vai kosmosā, kā jums patīk. Skaidrības labad es to uzzīmēju horizontāli.

Ko mēs darīsim ar šo segmentu? Šoreiz sagriezti. Kāds zāģē budžetu, kāds zāģē laulāto, kāds zāģē malku, un mēs sāksim zāģēt segmentu divās daļās. Segments ir sadalīts divās daļās, izmantojot kādu punktu, kas, protams, atrodas tieši uz tā:

Šajā piemērā punkts līniju sadala tādā veidā, ka līnija ir puse no līnijas garuma. VAIRĀK mēs varam teikt, ka punkts dala segmentu proporcijā ("viens pret divus"), skaitot no augšas.

Sausā matemātiskā valodā šo faktu raksta šādi: vai biežāk parastās proporcijas formā:. Segmentu attiecību parasti apzīmē ar grieķu burtu "lambda", šajā gadījumā:.

Proporciju ir viegli sastādīt citā secībā: - šis apzīmējums nozīmē, ka segments ir divreiz garāks nekā segments, bet tam nav fundamentālas nozīmes problēmu risināšanā. Jūs varat darīt, bet jūs varat to darīt.

Protams, segmentu var viegli sadalīt kādā citā aspektā, un kā koncepcijas pastiprinājumu - otrais piemērs:

Šeit attiecība ir patiesa:. Ja mēs veidojam proporciju tieši pretēji, tad iegūstam:.

Pēc tam, kad esam izdomājuši, ko šajā sakarā nozīmē sadalīt segmentu, pāriesim pie praktisko problēmu apsveršanas.

Ja ir zināmi divi plaknes punkti, tad tā punkta koordinātas, kas sadala segmentu, izsaka ar formulām:

No kurienes radās šīs formulas? Analītiskās ģeometrijas laikā šīs formulas tiek stingri iegūtas, izmantojot vektorus (kur mēs varam iziet bez tiem? \u003d)). Turklāt tie ir derīgi ne tikai Dekarta koordinātu sistēmai, bet arī patvaļīgai asīnu koordinātu sistēmai (skat. Nodarbību) Vektoru lineārā (ne) atkarība. Vektoru pamats). Tāds ir universālais uzdevums.

1. piemērs

Atrodiet punkta koordinātas, dalot segmentu proporcijā, ja punkti ir zināmi

Lēmums: Šajā problēmā. Izmantojot formulas segmenta sadalīšanai šajā ziņā, mēs atrodam punktu:

Atbilde:

Pievērsiet uzmanību aprēķina metodei: vispirms atsevišķi jāaprēķina skaitītājs un saucējs. Rezultāts bieži (bet ne vienmēr) ir trīs vai četru stāvu daļa. Pēc tam mēs atbrīvojamies no daudzstāvu frakcijas un veicam galīgos vienkāršojumus.

Uzdevumam nav nepieciešama zīmējuma veidošana, taču vienmēr ir lietderīgi to aizpildīt uz melnraksta:

Patiešām, attiecība ir apmierināta, tas ir, segments ir trīs reizes īsāks nekā segments. Ja proporcija nav acīmredzama, segmentus vienmēr var izmērīt muļķīgi ar parastu lineālu.

Ekvivalents otrais risinājums: tajā skaitīšana sākas no punkta un attiecība ir taisnīga: (cilvēku vārdiem sakot, segments ir trīs reizes garāks nekā segments). Saskaņā ar formulām segmenta sadalīšanai šajā ziņā:

Atbilde:

Ņemiet vērā, ka formulās jums vispirms jāpārvieto punkta koordinātas, jo mazais trilleris sākās ar to.

Var arī redzēt, ka otrais veids ir racionālāks vienkāršāku aprēķinu dēļ. Tomēr šo problēmu bieži risina "tradicionālajā" secībā. Piemēram, ja segmentu piešķir nosacījums, tad tiek pieņemts, ka jūs izveidosit proporciju, ja segments tiks dots, tad “klusējot” nozīmē proporciju.

Un es ienesu otro metodi tā iemesla dēļ, ka bieži uzdevuma nosacījumu tiek apzināti mēģināts sajaukt. Tāpēc ir ļoti svarīgi veikt aptuvenu rasējumu, lai, pirmkārt, pareizi analizētu stāvokli un, otrkārt, verifikācijas nolūkos. Tas ir kauns pieļaut kļūdas tik vienkāršā uzdevumā.

2. piemērs

Punkti tiek doti ... Atrast:

a) punkts, kas sadala segmentu attiecībā pret;
b) punkts, kas sadala segmentu attiecībā pret.

Šis ir piemērs “pats-pats” risinājumam. Pilns risinājums un atbilde apmācības beigās.

Dažreiz ir problēmas, kurās viens no segmenta galiem nav zināms:

3. piemērs

Punkts pieder līnijas segmentam. Ir zināms, ka segments ir divreiz garāks nekā segments. Atrodiet punktu, ja .

Lēmums: No nosacījuma, ka punkts dala segmentu attiecībās, skaitot no augšas, tas ir, proporcija ir taisnīga:. Saskaņā ar formulām segmenta sadalīšanai šajā ziņā:

Pašlaik mēs nezinām punkta koordinātas:, bet tā nav īpaša problēma, jo tos ir viegli izteikt no iepriekšminētajām formulām. Kopumā nav vērts neko izteikt, daudz vieglāk ir aizstāt noteiktus skaitļus un uzmanīgi rīkoties ar aprēķiniem:

Atbilde:

Lai pārbaudītu, varat ņemt segmenta galus un, izmantojot formulas tiešā secībā, pārliecināties, ka attiecība faktiski radīs punktu. Un, protams, protams, zīmējums nebūs lieks. Un, lai jūs beidzot pārliecinātu par rūtainā piezīmjdatora, vienkārša zīmuļa un lineāla priekšrocībām, es piedāvāju sarežģītu neatkarīga risinājuma problēmu:

4. piemērs

Punkts. Segments ir pusotru reizi īsāks nekā segments. Atrodiet punktu, ja ir zināmas punktu koordinātas .

Risinājums nodarbības beigās. Starp citu, tas nav vienīgais, ja jūs ejat atšķirīgu ceļu no izlases, tā nebūs kļūda, galvenais, lai atbildes sakristu.

Telpiskajiem segmentiem viss būs tieši tāds pats, ir pievienota tikai vēl viena koordināta.

Ja ir zināmi divi atstarpes punkti, tad tā punkta koordinātas, kas sadala segmentu, izsaka ar formulām:
.

5. piemērs

Punkti tiek doti. Atrodiet segmentam piederošā punkta koordinātas, ja tas ir zināms .

Lēmums: No nosacījuma izriet sakarība: ... Šis piemērs ir ņemts no reāla testa, un tā autors ļāva sev nedaudz palaidnībai (pēkšņi kāds paklupa) - bija racionālāk uzrakstīt proporciju šādā stāvoklī: .

Pēc segmenta vidusdaļas koordinātu formulām:

Atbilde:

3D rasējumus verifikācijas nolūkos ir daudz grūtāk izpildīt. Tomēr jūs vienmēr varat izveidot shematisku zīmējumu, lai vismaz saprastu nosacījumu - kuri segmenti ir jākorelē.

Neuztraucieties par atbildē iekļautajām frakcijām - tas ir bieži. Es to esmu teicis daudzas reizes, bet es atkārtošu: augstākajā matemātikā parasti tiek izmantotas parastās pareizās un nepareizās frakcijas. Atbilde formā darīs, bet opcija ar nepareizām frakcijām ir standarta.

Iesildīšanas uzdevums neatkarīgam risinājumam:

6. piemērs

Punkti tiek doti. Atrodiet punkta koordinātas, ja ir zināms, ka tas sadala segmentu attiecībā pret to.

Risinājums un atbilde stundas beigās. Ja ir grūti orientēties proporcijās, sekojiet shematiskajam zīmējumam.

Neatkarīgos un kontroles darbos aplūkotie piemēri ir atrodami gan paši, gan kā neatņemama sastāvdaļa lielākiem uzdevumiem. Šajā ziņā tipiska ir trijstūra smaguma centra atrašanas problēma.

Tāda veida uzdevums, kad viens no segmenta galiem nav zināms, es neredzu lielas jēgas izjaukt, jo viss izskatīsies kā plakans gadījums, izņemot to, ka ir nedaudz vairāk aprēķinu. Labāk atcerēsimies skolas gadus:

Līnijas viduspunkta formulas

Pat neapmācīti lasītāji var atcerēties, kā sadalīt segmentu uz pusēm. Segmenta sadalīšanas divās vienādās daļās problēma šajā ziņā ir īpašs segmenta sadalīšanas gadījums. Divu roku zāģis darbojas visdemokrātiskākajā veidā, un katrs kaimiņš pie galda saņem to pašu nūju:

Šajā svinīgajā stundā bungas sita, atzinīgi novērtējot ievērojamo proporciju. Un vispārējās formulas brīnumainā kārtā pārveidot par kaut ko pazīstamu un vienkāršu:

Ērts brīdis ir fakts, ka segmenta galu koordinātas var nesāpīgi pārkārtot:

Vispārējās formulās šāds grezns numurs, kā jūs zināt, nedarbojas. Un šeit tas nav īpašs, tāpēc patīkams sīkums.

Acīmredzama analoģija ir piemērojama telpiskajam gadījumam. Ja ir norādīti segmenta gali, tad tā viduspunkta koordinātas izsaka ar formulām:

7. piemērs

Paralēlogrammu piešķir tās virsotņu koordinātas. Atrodiet tā diagonāļu krustošanās punktu.

Lēmums: Interesenti var izgatavot zīmējumu. Īpaši iesaku grafiti tiem, kuri ir pilnībā aizmirsuši skolas ģeometrijas kursu.

Pazīstams īpašums ir tāds, ka paralelogrammas diagonāles tiek samazinātas uz pusi pēc to krustošanās vietas, tāpēc problēmu var atrisināt divējādi.

Pirmā metode: Apsveriet pretējās virsotnes ... Izmantojot formulas segmenta sadalīšanai uz pusēm, mēs atrodam diagonāles viduspunktu:

Zemāk esošajā rakstā tiks uzsvērti jautājumi par segmenta viduspunkta koordinātu atrašanu, ja kā sākotnējie dati ir tā galējo punktu koordinātas. Bet pirms sākt pētīt šo jautājumu, mēs ieviešam vairākas definīcijas.

1. definīcija

Sadaļa - taisna līnija, kas savieno divus patvaļīgus punktus, ko sauc par līnijas galiem. Piemēram, ļaujiet tai būt punktiem A un B un attiecīgi A segmentam.

Ja segments A B turpinās abos virzienos no punktiem A un B, mēs iegūstam līniju A B. Tad segments A B ir iegūtās līnijas daļa, ko ierobežo punkti A un B. Segments A B apvieno punktus A un B, kas ir tā gali, kā arī punktu kopu, kas atrodas starp. Ja, piemēram, ņemtu jebkuru patvaļīgu punktu K, kas atrodas starp punktiem A un B, mēs varam teikt, ka punkts K atrodas uz segmenta A B.

2. definīcija

Segmenta garums - attālums starp segmenta galiem noteiktā mērogā (vienības garuma segments). Segmenta A B garumu apzīmē šādi: A B.

3. definīcija

Viduspunkts - punkts, kas atrodas uz segmenta un ir vienādā attālumā no tā galiem. Ja segmenta A B viduspunkts tiek apzīmēts ar punktu C, tad vienlīdzība būs taisnība: A C \u003d C B

Sākotnējie dati: koordinātu līnija O x un nejauši punkti uz tās: A un B. Šie punkti atbilst reālajiem skaitļiem x A un x B C punkts - A B segmenta viduspunkts: jānosaka koordināta x C

Tā kā punkts C ir segmenta A B viduspunkts, tad būs spēkā šāda vienlīdzība: A C | \u003d | C B | ... Attālumu starp punktiem nosaka to koordinātu starpības modulis, t.i.

| A C | \u003d | C B | ⇔ x C - x A \u003d x B - x C

Tad ir iespējamas divas vienādības: x C - x A \u003d x B - x C un x C - x A \u003d - (x B - x C)

No pirmās vienādības mēs iegūstam C punkta koordinātu formulu: x C \u003d x A + x B 2 (puse no segmenta galu koordinātu summas).

No otrās vienlīdzības mēs iegūstam: x A \u003d x B, kas nav iespējams, jo sākotnējos datos neatbilst punkti. Tādējādi formula segmenta A B viduspunkta koordinātu noteikšanai ar galiem A (x A) un B (x B):

Iegūtā formula būs pamats segmenta viduspunkta koordinātu noteikšanai plaknē vai telpā.

Sākotnējie dati: taisnstūrveida koordinātu sistēma plaknē O x y, divi patvaļīgi punkti, kas nesakrīt ar dotajām koordinātām A x A, y A un B x B, y B. C punkts ir A segmenta B viduspunkts. C punktam ir jānosaka koordinātas x C un y C.

Paņemsim analīzei gadījumu, kad punkti A un B nesakrīt un neatrodas uz tās pašas koordinātu līnijas vai taisnas līnijas, kas ir perpendikulāra vienai no asīm. A x, A y; B x, B y un C x, C y - punktu A, B un C projekcijas uz koordinātu asīm (taisnas līnijas O x un O y).

Saskaņā ar konstrukciju līnijas A Ax, B B x, C C x ir paralēlas; arī taisnas līnijas ir paralēlas viena otrai. Kopā ar to, saskaņā ar Thales teorēmu, no vienādības A C \u003d C B izriet vienādības: A x C x \u003d C x B x un A y C y \u003d C y Y, un tās, savukārt, norāda, ka punkts C x ir segmenta vidusdaļa A x B x, un C y ir segmenta A y B y viduspunkts. Un tad, pamatojoties uz iepriekš iegūto formulu, mēs iegūstam:

x C \u003d x A + x B 2 un y C \u003d y A + y B 2

Tās pašas formulas var izmantot gadījumā, ja punkti A un B atrodas uz vienas un tās pašas koordinātu līnijas vai taisnas līnijas, kas ir perpendikulāra vienai asij. Mēs neveiksim detalizētu šīs lietas analīzi, mēs to izskatīsim tikai grafiski:

Apkopojot visu iepriekš minēto, segmenta A B viduspunkta koordinātas plaknē ar galu koordinātām A (x A, y A) un B (x B, y B) definēts kā:

(x A + x B 2, y A + y B 2)

Sākotnējie dati: koordinātu sistēma О x y z un divi patvaļīgi punkti ar norādītajām koordinātām A (x A, y A, z A) un B (x B, y B, z B). Ir jānosaka punkta C koordinātas, kas ir A segmenta B viduspunkts.

A x, A y, A z; B x, B y, B z un C x, C y, C z - visu norādīto punktu projekcijas uz koordinātu sistēmas ass.

Saskaņā ar Thales teorēmu, ir taisnība šādām vienādībām: A x C x \u003d C x B x, A y C y \u003d C y B y, A z C z \u003d C z B z

Tāpēc punkti C x, C y, C z ir attiecīgi segmentu A x B x, A y B y, A z B z viduspunkti. Tad lai noteiktu segmenta viduspunkta koordinātas telpā, ir spēkā šādas formulas:

x C \u003d x A + x B 2, y c \u003d y A + y B 2, z c \u003d z A + Z B 2

Iegūtās formulas piemēro arī gadījumos, kad punkti A un B atrodas uz vienas no koordinātu līnijām; taisnā līnijā, kas ir perpendikulāra vienai no asīm; vienā koordinātu plaknē vai plaknē, kas ir perpendikulāra vienai no koordinātu plaknēm.

Segmenta viduspunkta koordinātu noteikšana caur tā galu rādiusa vektoru koordinātām

Segmenta viduspunkta koordinātu atrašanas formulu var iegūt arī saskaņā ar vektoru algebrisko interpretāciju.

Sākotnējie dati: taisnstūrveida Dekarta koordinātu sistēma O x y, punkti ar norādītajām koordinātām A (x A, y A) un B (x B, x B). C punkts ir A segmenta B viduspunkts.

Saskaņā ar vektoru darbību ģeometrisko definīciju būs spēkā šāda vienādība: O C → \u003d 1 2 · O A → + O B →. C punkts šajā gadījumā ir paralelogrammas diagonāļu krustošanās punkts, kas uzbūvēts, pamatojoties uz vektoriem O A → un O B →, t.i. diagonāles viduspunkts.Punkta rādiusa vektora koordinātas ir vienādas ar punkta koordinātām, tad vienādības ir patiesas: O A → \u003d (x A, y A), O B → \u003d (x B, y B). Veiksim dažas operācijas ar vektoriem koordinātēs un iegūsim:

O C → \u003d 1 2 O A → + O B → \u003d x A + x B 2, y A + y B 2

Tāpēc punktam C ir koordinātas:

x A + x B 2, y A + y B 2

Pēc analoģijas tiek noteikta formula, kā atrast segmenta viduspunkta koordinātas telpā:

C (x A + x B 2, y A + y B 2, z A + z B 2)

Problēmu risināšanas piemēri segmenta viduspunkta koordinātu atrašanai

Starp uzdevumiem, kas saistīti ar iepriekš iegūto formulu izmantošanu, ir gan tie, kuros tieši tiek iesaistīts jautājums par segmenta viduspunkta koordinātu aprēķināšanu, gan uzdevumi, kas saistīti ar doto nosacījumu izvirzīšanu šim jautājumam: bieži tiek izmantots termins “mediāna”, mērķis ir atrast viena koordinātas. no segmenta galiem, kā arī izplatītas simetrijas problēmas, kuru risinājumam arī pēc šīs tēmas izpētes nevajadzētu radīt grūtības. Apsvērsim tipiskus piemērus.

1. piemērs

Sākotnējie dati: plaknē - punkti ar norādītajām koordinātām A (- 7, 3) un B (2, 4). Nepieciešams atrast segmenta A B viduspunkta koordinātas.

Lēmums

Apzīmējiet segmenta A B viduspunktu ar punktu C. Tās koordinātas tiks definētas kā segmenta galu koordinātu pussumma, t.i. punkti A un B

x C \u003d x A + x B 2 \u003d - 7 + 2 2 \u003d - 5 2 y C \u003d y A + y B 2 \u003d 3 + 4 2 \u003d 7 2

Atbilde: segmenta A koordinātas - B 2, 7 2.

2. piemērs

Sākotnējie dati: ir zināmas trijstūra A B C koordinātas: A (- 1, 0), B (3, 2), C (9, - 8). Jāatrod mediānas A garums.

Lēmums

1. Pēc problēmas hipotēzes M ir mediāna, un tāpēc M ir segmenta B C viduspunkts. Pirmkārt, mēs atrodam segmenta B C viduspunkta koordinātas, t.i. punkts M:

x M \u003d x B + x C 2 \u003d 3 + 9 2 \u003d 6 y M \u003d y B + y C 2 \u003d 2 + (- 8) 2 \u003d - 3

1. Tā kā tagad mēs zinām mediānas abu galu koordinātas (punkti A un M), mēs varam izmantot formulu, lai noteiktu attālumu starp punktiem un aprēķinātu mediānas A M garumu:

A M \u003d (6 - (- 1)) 2 + (- 3 - 0) 2 \u003d 58

Atbilde: 58

3. piemērs

Sākotnējie dati: trīsdimensiju telpas taisnstūra koordinātu sistēmā tiek dots paralēles A B C D A 1 B 1 C 1 D 1. Norādītas punkta C 1 (1, 1, 0) koordinātas, kā arī definēts punkts M, kas ir diagonāles B D 1 vidusdaļa un kam ir koordinātas M (4, 2, - 4). Ir jāaprēķina A punkta koordinātas.

Lēmums

Paralēlskaldņa diagonālēm ir krustojums vienā punktā, kas ir visu diagonāļu viduspunkts. Balstoties uz šo paziņojumu, var atcerēties, ka punkts M, kas zināms no problēmas apstākļiem, ir segmenta A C 1 viduspunkts. Balstoties uz formulu segmenta viduspunkta koordinātu atrašanai telpā, mēs atrodam punkta A koordinātas: x M \u003d x A + x C 1 2 ⇒ x A \u003d 2 x M - x C 1 \u003d 2 4 - 1 + 7 y M \u003d y A + y C 1 2 ⇒ y A \u003d 2 y M - y C 1 \u003d 2 2 - 1 \u003d 3 z M \u003d z A + z C 1 2 ⇒ z A \u003d 2 z M - z C 1 \u003d 2 (- 4) - 0 \u003d - 8

Atbilde: punkta A koordinātas (7, 3, - 8).

Ja tekstā pamanāt kļūdu, lūdzu, atlasiet to un nospiediet Ctrl + Enter

Kā atrast līnijas viduspunkta koordinātas
Vispirms izdomāsim, kāds ir segmenta vidusdaļa.
Segmenta viduspunkts ir punkts, kas pieder šim segmentam un atrodas tajā pašā attālumā no tā galiem.

Šāda punkta koordinātas ir viegli atrast, ja ir zināmas šī segmenta galu koordinātas. Šajā gadījumā segmenta viduspunkta koordinātas būs vienādas ar pusi no segmenta galu atbilstošo koordinātu summas.
Segmenta viduspunkta koordinātas bieži atrod, risinot vidējā, centra līnijas u.c. problēmas.
Apsveriet segmenta viduspunkta koordinātu aprēķinu diviem gadījumiem: kad segments ir dots plaknē un dots telpā.
Ļaujiet segmentam plaknē dot divus punktus ar koordinātām un. Tad PH segmenta viduspunkta koordinātas aprēķina pēc formulas:

Ļaujiet segmentam telpā dot divus punktus ar koordinātām un. Tad PH segmenta viduspunkta koordinātas aprēķina pēc formulas:

Piemērs.
Atrodiet punkta K koordinātas - MO vidusdaļu, ja M (-1; 6) un O (8; 5).

Lēmums.
Tā kā punktiem ir divas koordinātas, tas nozīmē, ka segments ir noteikts plaknē. Mēs izmantojam atbilstošās formulas:

Līdz ar to MO vidum būs koordinātas K (3.5; 5.5).

Atbilde. K (3,5; 5,5).