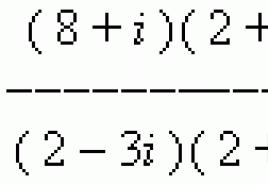복소수 이론 및 예. 복소수

복소수

상상의 그리고 복소수. 가로 좌표 및 세로 좌표

복소수. 복소수를 켤레.

복소수 연산. 기하학적

복소수의 표현. 복잡한 평면.

복소수의 계수 및 인수. 삼각법

복소수 형식. 복잡한 작업

삼각함수 형태의 숫자. 무아브르 공식.

에 대한 기본 정보 상상의 그리고 복소수 "허수 및 복소수"섹션에 나와 있습니다. 경우에 대한 이차 방정식을 풀 때 새로운 유형의 이러한 숫자에 대한 필요성이 나타났습니다.디< 0 (здесь 디는 이차 방정식의 판별식입니다). 오랫동안 이 숫자는 물리적 용도를 찾지 못했기 때문에 "허수"라고 불렸습니다. 그러나 이제 그들은 다양한 물리학 분야에서 매우 널리 사용됩니다.

및 기술: 전기 공학, 수력 및 공기 역학, 탄성 이론 등

복소수 다음과 같이 작성됩니다.에이+비. 여기 ㅏ그리고 비 – 실수 , ㅏ 나 – 상상의 단위.이자형. 나 2 = –1. 숫자 ㅏ~라고 불리는 횡좌표, ㅏ b - 세로 좌표복소수a + b .두 개의 복소수에이+비그리고 아비 ~라고 불리는 결합한복소수.

주요 계약:

1. 실수ㅏ형식으로 작성할 수도 있습니다.복소수:+ 0 나또는 ㅏ - 0 나. 예를 들어 항목 5 + 0나그리고 5 - 0 나같은 숫자를 의미 5 .

2. 복소수 0 + 바이~라고 불리는 순전히 상상의 숫자. 녹음바이0과 같은 의미 + 바이.

3. 두 개의 복소수에이+비 그리고c + 디다음과 같은 경우 동등한 것으로 간주됩니다.a = c그리고 b = d. 그렇지 않으면 복소수는 같지 않습니다.

덧셈. 복소수의 합에이+비그리고 c + 디복소수(a+c ) + (b+d ) 나 .이런 식으로, 추가될 때 복소수, 가로 좌표 및 세로 좌표는 별도로 추가됩니다.

이 정의는 일반 다항식을 다루는 규칙을 따릅니다.

빼기. 두 복소수의 차이에이+비(감소) 및 c + 디(빼기)는 복소수(a-c ) + (b-d ) 나 .

이런 식으로, 두 개의 복소수를 뺄 때 가로 좌표와 세로 좌표는 별도로 뺍니다.

곱셈. 복소수의 곱에이+비그리고 c + 디 복소수라고 합니다.

(AC-BD ) + (광고+BC ) 나 .이 정의는 두 가지 요구 사항에서 비롯됩니다.

1) 숫자 에이+비그리고 c + 디대수처럼 곱해야 합니다이항,

2) 번호 나주요 속성이 있습니다:나 2 = – 1.

예시 ( 에이 + 바이 )(아비) = 에이 2 +b 2 . 따라서, 일하다

두 개의 켤레 복소수는 실수와 같습니다.

정수.

분할. 복소수 나누기에이+비 (나누는) 다른 사람에게c + 디(분할기) - 세 번째 숫자를 찾는 것을 의미합니다.전자 + 파이(채팅), 제수를 곱하면c + 디, 결과적으로 배당금a + b .

제수가 0이 아니면 항상 나눗셈이 가능합니다.

예시 찾기(8+나 ) : (2 – 3 나) .

솔루션: 이 비율을 분수로 다시 작성해 보겠습니다.

분자와 분모에 2 + 3 곱하기나

그리고 모든 변환을 수행한 후 다음을 얻습니다.

복소수의 기하학적 표현. 실수는 숫자 선의 점으로 표시됩니다.

여기 요점이 있습니다 ㅏ숫자 -3, 점을 의미비는 숫자 2이고 영형- 영. 대조적으로, 복소수는 좌표 평면의 점으로 표시됩니다. 이를 위해 두 축에서 동일한 축척을 갖는 직사각형(직교) 좌표를 선택합니다. 그럼 복소수에이+비 점으로 표시됩니다 횡좌표가 있는 P a와 세로좌표 b (그림 참조). 이 좌표계를 복잡한 평면 .

기준 치수 복소수를 벡터의 길이라고 합니다.OP, 좌표에 복소수를 나타내는 ( 통합) 비행기. 복소수 계수에이+비로 표시 | 에이+비| 또는 편지 아르 자형

강의 계획.

1. 조직적 순간.

2. 자료 발표.

3. 숙제.

4. 수업을 요약합니다.

수업 중

I. 조직적 순간.

Ⅱ. 자료 발표.

동기 부여.

실수 집합의 확장은 새로운 숫자(허수)가 실수에 추가된다는 사실로 구성됩니다. 이 숫자의 도입은 실수 집합의 음수에서 근을 추출할 수 없다는 것과 관련이 있습니다.

복소수의 개념 소개.

실수를 보완하는 허수는 다음과 같이 작성됩니다. 바이, 어디 나는 허수 단위이고, 나는 2 = - 1.

이를 바탕으로 다음과 같은 복소수의 정의를 얻습니다.

정의. 복소수는 다음 형식의 표현입니다. 에이+비, 어디 ㅏ그리고 비실수입니다. 이 경우 다음 조건이 충족됩니다.

a) 두 개의 복소수 a 1 + b 1 나그리고 a 2 + b 2 나동일한 경우에만 1 = 2, b1=b2.

b) 복소수의 추가는 다음 규칙에 따라 결정됩니다.

(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.

c) 복소수의 곱셈은 다음 규칙에 따라 결정됩니다.

(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.

복소수의 대수적 형태.

형식으로 복소수 쓰기 에이+비복소수의 대수적 형태라고 하며, 여기서 ㅏ- 실제 부분 바이는 허수부이고, 비는 실수입니다.

복소수 에이+비실수부와 허수부가 0이면 0으로 간주됩니다. a=b=0

복소수 에이+비~에 b = 0실제 숫자로 간주 ㅏ: 에이 + 0i = 에이.

복소수 에이+비~에 에이 = 0순전히 상상이라고 하며 다음과 같이 표시됩니다. 바이: 0 + 바이 = 바이.

두 개의 복소수 z = a + 바이그리고 = 에이 – 바이, 허수부의 부호만 다른 것을 켤레라고 합니다.

대수 형식의 복소수에 대한 작업.

다음 연산은 대수 형식의 복소수에 대해 수행할 수 있습니다.

1) 추가.

정의. 복소수의 합 z 1 = a 1 + b 1 i그리고 z 2 = a 2 + b 2 i복소수라고 함 지, 실수 부분은 실수 부분의 합과 같습니다. z1그리고 z2, 그리고 허수 부분은 숫자의 허수 부분의 합입니다 z1그리고 z2, 그건 z = (a 1 + a 2) + (b 1 + b 2)i.

번호 z1그리고 z2용어라고 합니다.

복소수를 더하면 다음과 같은 속성이 있습니다.

1º. 교환성: z1 + z2 = z2 + z1.

2º. 연관성: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).

3º. 복소수 -아 -비복소수의 반대라고 합니다 z = a + 바이. 복소수의 반대 복소수 지, 표시 -지. 복소수의 합 지그리고 -지 0과 같음: z + (-z) = 0

예 1: 추가 (3 - i) + (-1 + 2i).

(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) 빼기.

정의.복소수에서 빼기 z1복소수 z2 지,무엇 z + z 2 = z 1.

정리. 복소수의 차이는 존재하며 또한 고유합니다.

예 2: 빼기 (4 - 2i) - (-3 + 2i).

(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) 나는 = 7 - 4i.

3) 곱셈.

정의. 복소수의 곱 z 1 = a 1 + b 1 i그리고 z 2 \u003d a 2 + b 2 i복소수라고 함 지, 평등으로 정의: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.

번호 z1그리고 z2요인이라고 합니다.

복소수의 곱셈에는 다음과 같은 속성이 있습니다.

1º. 교환성: z 1 z 2 = z 2 z 1.

2º. 연관성: (z 1 z 2)z 3 = z 1 (z 2 z 3)

3º. 덧셈에 대한 곱셈의 분포:

(z 1 + z 2) z 3 \u003d z 1 z 3 + z 2 z 3.

4º. z \u003d (a + bi) (a-bi) \u003d a 2 + b 2는 실수입니다.

실제로 복소수의 곱셈은 합에 합을 곱하고 실수부와 허수부를 분리하는 규칙에 따라 수행됩니다.

다음 예에서 두 가지 방법으로 복소수의 곱셈을 고려하십시오. 규칙에 의한 방법과 합에 합을 곱하는 방법입니다.

예 3: 곱하기 (2 + 3i) (5 – 7i).

1 방법. (2 + 3i) (5 – 7i) = (2× 5 – 3× (-7)) + (2× (-7) + 3× 5)i = = (10 + 21) + (- 14 + 15 ) 나는 = 31 + 나는.

2 방법. (2 + 3i) (5 - 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.

4) 부문.

정의. 복소수 나누기 z1복소수로 z2, 그러한 복소수를 찾는 것을 의미합니다 지, 무엇 z z 2 = z 1.

정리.복소수의 몫은 존재하며 다음과 같은 경우 고유합니다. z2 ≠ 0 + 0i.

실제로 복소수의 몫은 분자와 분모에 분모의 켤레를 곱하여 구합니다.

허락하다 z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, 그 다음에

.

다음 예에서는 공식으로 나누기를 수행하고 분모의 켤레에 의한 곱셈 규칙을 수행합니다.

예 4. 몫 찾기 .

5) 양의 정수 거듭제곱으로 올립니다.

a) 상상적 통일성의 힘.

평등을 이용하다 나는 2 \u003d -1, 허수 단위의 양의 정수 거듭제곱을 정의하는 것은 쉽습니다. 우리는 다음을 가지고 있습니다:

나는 3 \u003d 나는 2 나는 \u003d -나는,

나는 4 \u003d 나는 2 나는 2 \u003d 1,

나는 5 \u003d 나는 4 나는 \u003d 나는,

나는 6 \u003d 나는 4 나는 2 \u003d -1,

나는 7 \u003d 나는 5 나는 2 \u003d -나는,

나는 8 = 나는 6 나는 2 = 1등.

이것은 학위 값을 보여줍니다 에, 어디 N- 지표가 증가할 때 주기적으로 반복되는 양의 정수 4 .

따라서 숫자를 높이려면 나양의 정수 거듭제곱으로 지수를 나눕니다. 4 그리고 세우다 나지수가 나눗셈의 나머지인 거듭제곱입니다.

예 5 계산: (나는 36 + 나는 17) 나는 23.

나는 36 = (나는 4) 9 = 1 9 = 1,

나는 17 = 나는 4 × 4+1 = (나는 4) 4 × 나는 = 1 나는 = 나는.

나는 23 = 나는 4 × 5+3 = (나는 4) 5 × 나는 3 = 1 나는 3 = - 나는.

(나는 36 + 나는 17) 나는 23 \u003d (1 + 나는) (- 나는) \u003d - 나는 + 1 \u003d 1 - 나는.

b) 복소수를 양의 정수 거듭제곱으로 올리는 것은 동일한 복소수를 곱하는 특수한 경우이기 때문에 이항식을 해당 거듭제곱으로 올리는 규칙에 따라 수행됩니다.

예 6 계산: (4 + 2i) 3

(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.

복소수는 우리에게 친숙한 실수 집합의 최소 확장입니다. 근본적인 차이점은 제곱이 -1을 제공하는 요소가 나타난다는 것입니다. 나, 또는 .

모든 복소수는 두 부분으로 구성됩니다. 현실과 상상의:

따라서 실수의 집합은 허수부가 0인 복소수의 집합과 일치한다는 것이 분명합니다.

복소수 집합에 대해 가장 많이 사용되는 모델은 일반 평면입니다. 각 점의 첫 번째 좌표는 실수 부분이 되고 두 번째 좌표는 허수가 됩니다. 그러면 복소수 자체의 역할은 시작점이 점 (0,0)인 벡터가 됩니다.

복소수에 대한 연산.

실제로 복소수 집합의 모델을 고려하면 두 복소수의 덧셈(뺄셈)과 곱셈이 벡터에 대한 해당 연산과 동일한 방식으로 수행됨을 직관적으로 알 수 있습니다. 또한 이 연산의 결과가 다시 벡터이기 때문에 벡터의 외적을 의미합니다.

1.1 추가.

(보시다시피 이 작업은 정확히 에 해당합니다.)

1.2 빼기, 마찬가지로 다음 규칙에 따라 수행됩니다.

2. 곱셈.

3. 부문.

곱셈의 역연산으로 간단히 정의됩니다.

삼각법 형태.

복소수 z의 계수는 다음과 같습니다.

,

이것은 다시 단순히 벡터(a,b)의 모듈러스(길이)임이 분명합니다.

대부분의 경우 복소수의 계수는 다음과 같이 표시됩니다. ρ.

그것은 밝혀

z = ρ(cosφ+isinφ).

다음은 복소수를 쓰는 삼각법 형식에서 직접 따릅니다. 방식 :

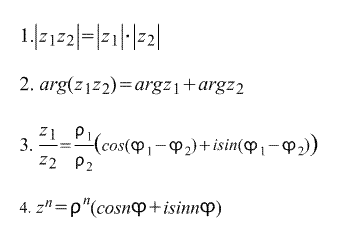
마지막 공식은 드무아브르 공식. 공식은 그것에서 직접 파생됩니다. 복소수의 n번째 근:

따라서 복소수 z의 n번째 근이 있습니다.