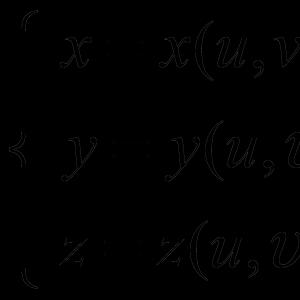The equation of a straight line in segments has the form. Equation of a straight line in segments - description, examples, problem solving
We continue to study the section “The equation of a straight line on a plane” and in this article we will analyze the topic “The equation of a straight line in segments”. We will successively consider the form of the equation of a straight line in segments, the construction of a straight line, which is given by this equation, the transition from the general equation of a straight line to the equation of a straight line in segments. All this will be accompanied by examples and analysis of problem solving.
Let a rectangular coordinate system O x y be located on the plane.
A straight line on a plane in the Cartesian coordinate system O x y is given by an equation of the form x a + y b = 1 , where a and b are some non-zero real numbers whose values are equal to the lengths of the segments cut off by the straight line on the axes O x and O y . The lengths of the segments are considered from the origin of coordinates.
As we know, the coordinates of any of the points belonging to a straight line given by the equation of a straight line satisfy the equation of this straight line. Points a , 0 and 0 , b belong to this straight line, since a a + 0 b = 1 ⇔ 1 ≡ 1 and 0 a + b b = 1 ⇔ 1 ≡ 1 . Points a , 0 and b , 0 are located on the coordinate axes O x and O y and are removed from the origin by a and b units. The direction in which you want to postpone the length of the segment is determined by the sign that comes before the numbers a and b. The “-” sign means that the length of the segment must be plotted in the negative direction of the coordinate axis.
Let us explain all of the above by placing the lines relative to a fixed Cartesian coordinate system O x y in a schematic drawing. The equation of a straight line in the segments x a + y b = 1 is used to construct a straight line in the Cartesian coordinate system O x y . To do this, we need to mark points a, 0 and b, 0 on the axes, and then connect these points with a line using a ruler.
The drawing shows cases where the numbers a and b have different signs, and, therefore, the lengths of the segments are plotted in different directions of the coordinate axes.
Consider an example.
Example 1
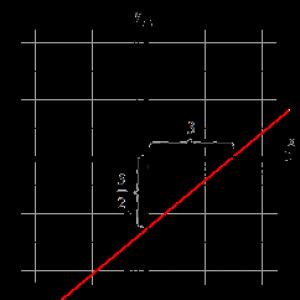
The straight line is given by the straight line equation in segments of the form x 3 + y - 5 2 = 1 . It is necessary to build this line on the plane in the Cartesian coordinate system O x y .
Solution
Using the equation of a straight line in segments, we determine the points through which the straight line passes. It's 3 0 0 - 5 2 . Let's mark them and draw a line.
Reduction of the general equation of a straight line to the equation of a straight line in segments
The transition from the given equation of a straight line to the equation of a straight line in segments makes it easier for us to solve various problems. Having the complete general equation of a straight line, we can obtain the equation of a straight line in segments.
The complete general equation of a straight line in the plane has the form A x + B y + C = 0, where A, B and C are not equal to zero. We transfer the number C to the right side of the equality, divide both parts of the resulting equality by - C. At the same time, we send the coefficients for x and y to the denominators:
A x + B y + C = 0 ⇔ A x + B y = - C ⇔ ⇔ A - C x + B - C y = 1 ⇔ x - C A + y - C B = 1
To implement the last transition, we used the equality p q = 1 q p , p ≠ 0 , q ≠ 0 .
As a result, we have made the transition from the general equation of the straight line A x + B y + C = 0 to the equation of the straight line in the segments x a + y b = 1 , where a = - C A , b = - C B .
Let's consider the following example.
Example 2
Let's make the transition to the equation of a straight line in segments, having the general equation of a straight line x - 7 y + 1 2 = 0 .
Solution
We transfer one second to the right side of the equality x - 7 y + 1 2 = 0 ⇔ x - 7 y = - 1 2 .
Divide both sides of the equation by - 1 2: x - 7 y = - 1 2 ⇔ 1 - 1 2 x - 7 - 1 2 y = 1 .
Let's transform the resulting equality to the desired form: 1 - 1 2 x - 7 - 1 2 y = 1 ⇔ x - 1 2 + y 1 14 = 1 .
We have obtained the equation of a straight line in segments.
Answer: x - 1 2 + y 1 14 = 1
In cases where a straight line is given by a canonical or parametric equation of a straight line on a plane, then we first pass to the general equation of a straight line, and then to the equation of a straight line in segments.
Going from the equation of a straight line in segments and the general equation of a straight line is simple: we transfer the unit from the right side of the equation of a straight line in segments of the form x a + y b \u003d 1 to the left side with the opposite sign, we select the coefficients in front of the unknowns x and y.
x a + y b = 1 ⇔ x a + y b - 1 = 0 ⇔ 1 a x + 1 b y - 1 = 0
We obtain the general equation of a straight line, from which we can pass to any other form of the equation of a straight line in a plane. We analyzed the transition process in detail in the topic “Reducing the general equation of a straight line to other types of a straight line equation”.
Example 3
The equation of a straight line in segments has the form x 2 3 + y - 12 = 1. It is necessary to write the general equation of a straight line in a plane.
Solution
It operates according to a previously described algorithm:
x 2 3 + y - 12 = 1 ⇔ 1 2 3 x + 1 - 12 y - 1 = 0 ⇔ ⇔ 3 2 x - 1 12 y - 1 = 0
Answer: 3 2 x - 1 12 y - 1 = 0
If you notice a mistake in the text, please highlight it and press Ctrl+Enter
Straight line equation , where a and b some real numbers other than zero is called equation of a straight line in segments. This name is not accidental, since the absolute values of numbers a and b equal to the lengths of the segments that the straight line cuts off on the coordinate axes Ox and Oy respectively (segments are counted from the origin). Thus, the equation of a straight line in segments makes it easy to build this straight line in a drawing. To do this, mark points with coordinates and in a rectangular coordinate system on the plane, and use a ruler to connect them with a straight line.
For example, let's build a straight line given by an equation in segments of the form . Mark the dots and connect them.
You can get detailed information about this type of equation of a straight line on a plane in the article equation of a straight line in segments.
Top of page
End of work -
This topic belongs to:
Algebra and analytic geometry. The concept of a matrix, operations on matrices and their properties
The concept of matrix operations on matrices and their properties .. a matrix is a rectangular table made up of numbers that cannot be .. and matrix addition is an element-wise operation ..
If you need additional material on this topic, or you did not find what you were looking for, we recommend using the search in our database of works:
What will we do with the received material:
If this material turned out to be useful for you, you can save it to your page on social networks:
| tweet |
All topics in this section:
Definition of differentiability
The operation of finding the derivative is called differentiation of a function. A function is said to be differentiable at some point if it has a finite derivative at that point, and
Differentiation rule
Corollary 1. The constant factor can be taken out of the sign of the derivative:
The geometric meaning of the derivative. Tangent equation
The angle of inclination of the straight line y \u003d kx + b is the angle measured from the position
The geometric meaning of the derivative of a function at a point
Consider the secant AB of the graph of the function y = f(x) such that points A and B have coordinates, respectively
Solution
The function is defined for all real numbers. Since (-1; -3) is the point of contact, then
Necessary conditions for an extremum and sufficient conditions for an extremum
Definition of an increasing function. The function y = f(x) increases on the interval X if for any
Sufficient criteria for the extremum of a function
To find the maxima and minima of the function, you can use any of the three sufficient signs of an extremum. Although the most common and convenient is the first of them.
Basic properties of a definite integral. Property 1. The derivative of a definite integral with respect to the upper limit is equal to the integrand into which, instead of a variable, is integrated
Newton-Leibniz formula (with proof)
Newton-Leibniz formula. Let the function y = f(x) be continuous on a segment and F(x) be one of the antiderivatives of the function on this segment, then
Let some affine coordinate system OXY be given.
Theorem 2.1. Any straight l coordinate system OX is given by a linear equation of the form
A x+ B y+ C = O, (1)
where A, B, C R and A 2 + B 2 0. Conversely, any equation of the form (1) defines a straight line.
Equation of the form (1) - general equation of a straight line .
Let in equation (1) all the coefficients A, B and C be non-zero. Then
Ah-By=-C, and .
Let's denote -C/A=a, -C/B=b. Get
-line segment equation .
Indeed, the numbers |a| and |b| indicate the size of the segments cut off by a straight line l on the OX and OY axes, respectively.
Let the line l is given by the general equation (1) in a rectangular coordinate system and let the points M 1 (x 1, y 1) and M 2 (x 2, y 2) belong l. Then
A x 1 + B at 1 + C = A X 2 + B at 2 + C, that is, A( x 1 -x 2) + B( at 1 -at 2) = 0.
The last equality means that the vector \u003d (A, B) is orthogonal to the vector \u003d (x 1 -x 2, y 1 -y 2). those. The vector (A, B) is called normal vector of the line l.
Consider the vector = (-B, A). Then
A(-B)+BA=0. those. ^ .
Therefore, the vector \u003d (-B, A) is the direction vector of the spicy l.
Parametric and canonical equations of a straight line
Equation of a straight line passing through two given points
Let the straight line be given in the affine coordinate system (0, X, Y) l, its direction vector = (m,n) and the point M 0 ( x 0 ,y 0) owned l. Then for an arbitrary point M ( x,at) of this line we have
and since then 
.
If we designate and
The radius vectors of the points M and M 0 , respectively, then
- equation of a straight line in vector form.
Because =( X,at), =(X 0 ,at 0), then
x= x 0 + mt,
y= y 0 + nt
- parametric equation of a straight line .
Hence it follows that
- canonical equation of a straight line .
Finally, if on a straight line l two points M 1 ( X 1 ,at 1) and
M2( x 2 ,at 2), then the vector =( X 2 -X 1 ,y 2 -at 1) is guiding straight line vector l. Then
- equation of a line passing through two given points.
Mutual arrangement of two straight lines.
Let straight l 1 and l 2 are given by their general equations
l 1: A 1 X+ In 1 at+ С 1 = 0, (1)
l 2: A 2 X+ B 2 at+ C 2 = 0.
Theorem. Let straight l 1 and l 2 are given by equations (1). Then and only then:
1) lines intersect when there is no number λ such that
A 1 =λA 2 , B 1 =λB 2 ;
2) the lines coincide when there is a number λ such that
A 1 =λA 2 , B 1 =λB 2 , C 1 =λC 2 ;
3) lines are distinct and parallel when there is a number λ such that
A 1 \u003d λA 2, B 1 \u003d λB 2, C 1 λC 2.
bundle of straight lines
A bunch of straight lines is the collection of all lines in the plane passing through some point called center beam.
To specify the beam equation, it suffices to know any two straight lines l 1 and l 2 passing through the center of the beam.
Let the lines in the affine coordinate system l 1 and l 2 are given by the equations
l 1:A1 x+B1 y+ C1 = 0,
l 2:A2 x+ B2 y+ C2 = 0.
The equation:
A 1 x+B1 y+ С + λ (A 2 X+ B 2 y+ C) = 0
- the equation of a pencil of lines defined by the equations l 1 and l 2.
In what follows, by the coordinate system we mean the rectangular coordinate system .
Conditions for parallelism and perpendicularity of two lines
Let the lines l 1 and l 2. with their general equations; = (A 1 ,B 1), = (A 2 ,B 2) are the normal vectors of these lines; k 1 = tanα 1 , k 2 = tgα 2 – slope coefficients; =( m 1 ,n 1), (m 2 ,n 2) are direction vectors. Then, direct l 1 and l 2 are parallel if and only if one of the following conditions is true:
or either k 1 =k 2 or .
Let it be straight now l 1 and l 2 are perpendicular. Then, obviously, , that is, A 1 A 2 + B 1 B 2 = 0.
If straight l 1 and l 2 are given respectively by the equations
l 1: at=k 1 x+ b 1 ,
l 2: at=k 2 x+ b 2 ,
then tgα 2 = tg(90º+α) = 
.
Hence it follows that
Finally, if and are the direction vectors of the lines, then ^ , i.e.
m 1 m 2 + n 1 n 2 = 0
The last relation expresses the necessary and sufficient condition for two planes to be perpendicular.
Angle between two lines
At an angle φ between two lines l 1 and l 2 we will understand the smallest angle through which one line must be rotated so that it becomes parallel to another line or coincides with it, that is, 0 £ φ £
Let the lines be given by general equations. It's obvious that
cosφ= 
Let it be straight now l 1 and l 2 is given by equations with slope coefficients k 1 in k 2 respectively. Then
Obviously, that is ( X-X 0) + B( at-at 0) + C( z-z 0) = 0
Let's open the brackets and denote D \u003d -A x 0 - B at 0 - C z 0 . Get
A x+ B y+ C z+ D = 0 (*)
- general plane equation or general plane equation.
Theorem 3.1 The linear equation (*) (A 2 +B 2 +C 2 ≠ 0) is the equation of the plane and vice versa, any equation of the plane is linear.
1) D = 0, then the plane passes through the origin.
2) A \u003d 0, then the plane is parallel to the OX axis
3) A \u003d 0, B \u003d 0, then the plane is parallel to the OXY plane.
Let all the coefficients in the equation be nonzero.
- equation of a plane in segments. The numbers |a|, |b|, |c| indicate the size of the segments cut off by the plane on the coordinate axes.
Equation of a straight line in segments
Let the general equation of a straight line be given:
The equation of a straight line in segments, where are the segments that the straight line cuts off on the corresponding coordinate axes.
Construct a straight line given by the general equation:
From which, you can build the equation of this straight line in segments:
Mutual arrangement of straight lines on a plane.
Statement 1.
In order for the lines and given by the equations:
Coincident, necessary and sufficient that:
Proof: and coincide, their direction vectors and are collinear, i.e.:
Let's take the point M 0 with these straight lines, then:
Multiplying the first equation by and adding to the second, due to (2) we get:
So, formulas (2), (3) and (4) are equivalent. Let (2) hold; then the equations of the system (*) are equivalent; the corresponding lines coincide.
Statement 2.
The lines and given by the equations (*) are parallel and do not coincide if and only if:
Proof:
Let them not match:
Inconsistent, i.e., according to the Kronecker-Capelli theorem:
This is possible only if:
That is, under condition (5).
When the first equality (5) is fulfilled, - non-fulfillment of the second equality gives the inconsistency of the system (*) the lines are parallel and do not coincide.
Remark 1.
Polar coordinate system.
We fix a point on the plane and call it a pole. The ray emanating from the pole is called the polar axis.
We choose a scale for measuring the lengths of segments and agree that the counterclockwise rotation around m will be considered positive. Consider any point on a given plane, denote by its distance to the pole and call it the polar radius. The angle by which the polar axis must be rotated so that it coincides with is denoted by and will be called the polar angle.
Definition 3.
The polar coordinates of a point are its polar radius and polar angle:
Remark 2. at the pole. The value for points other than a point is determined up to a term.
Consider a Cartesian rectangular coordinate system: the pole coincides with the origin, and the polar axis coincides with the positive semi-axis. Here. Then:
What is the relationship between rectangular Cartesian and polar coordinate systems.
Bernoulli's lemniscate equation. Write it down in polar coordinates.
Normal equation of a straight line in a plane. Let the polar axis coincide with, - the axis passing through the origin. Let:
Let then:
Condition (**) for a dot:
Equation of a straight line in the polar coordinate system.
Here - the length drawn from the origin to the straight line, - the angle of inclination of the normal to the axis.
Equation (7) can be rewritten:
Normal equation of a straight line in a plane.
Properties of a straight line in Euclidean geometry.
There are infinitely many lines that can be drawn through any point.
Through any two non-coinciding points, there is only one straight line.
Two non-coincident lines in the plane either intersect at a single point, or are
parallel (follows from the previous one).
In three-dimensional space, there are three options for the relative position of two lines:
- lines intersect;
- straight lines are parallel;
- straight lines intersect.
Straight line- algebraic curve of the first order: in the Cartesian coordinate system, a straight line
is given on the plane by an equation of the first degree (linear equation).
General equation of a straight line.
Definition. Any line in the plane can be given by a first order equation
Ah + Wu + C = 0,
and constant A, B not equal to zero at the same time. This first order equation is called general
straight line equation. Depending on the values of the constants A, B and WITH The following special cases are possible:
. C = 0, A ≠ 0, B ≠ 0- the line passes through the origin
. A = 0, B ≠0, C ≠0 ( By + C = 0)- straight line parallel to the axis Oh
. B = 0, A ≠ 0, C ≠ 0 ( Ax + C = 0)- straight line parallel to the axis OU
. B = C = 0, A ≠ 0- the line coincides with the axis OU
. A = C = 0, B ≠ 0- the line coincides with the axis Oh
The equation of a straight line can be represented in various forms depending on any given
initial conditions.
Equation of a straight line by a point and a normal vector.
Definition. In a Cartesian rectangular coordinate system, a vector with components (A, B)
perpendicular to the line given by the equation
Ah + Wu + C = 0.
Example. Find the equation of a straight line passing through a point A(1, 2) perpendicular to the vector (3, -1).
Solution. Let's compose at A \u003d 3 and B \u003d -1 the equation of the straight line: 3x - y + C \u003d 0. To find the coefficient C
we substitute the coordinates of the given point A into the resulting expression. We get: 3 - 2 + C = 0, therefore
C = -1. Total: the desired equation: 3x - y - 1 \u003d 0.
Equation of a straight line passing through two points.
Let two points be given in space M 1 (x 1 , y 1 , z 1) and M2 (x 2, y 2 , z 2), then straight line equation,
passing through these points:
If any of the denominators is equal to zero, the corresponding numerator should be set equal to zero. On the
plane, the equation of a straight line written above is simplified:
if x 1 ≠ x 2 and x = x 1, if x 1 = x 2 .
Fraction = k called slope factor straight.
Example. Find the equation of a straight line passing through the points A(1, 2) and B(3, 4).
Solution. Applying the above formula, we get:
Equation of a straight line by a point and a slope.
If the general equation of a straight line Ah + Wu + C = 0 bring to the form:
and designate 
, then the resulting equation is called
equation of a straight line with slope k.
The equation of a straight line on a point and a directing vector.
By analogy with the point considering the equation of a straight line through the normal vector, you can enter the task
a straight line through a point and a direction vector of a straight line.
Definition. Every non-zero vector (α 1 , α 2), whose components satisfy the condition
Aα 1 + Bα 2 = 0 called direction vector of the straight line.
Ah + Wu + C = 0.
Example. Find the equation of a straight line with direction vector (1, -1) and passing through point A(1, 2).
Solution. We will look for the equation of the desired straight line in the form: Ax + By + C = 0. According to the definition,
coefficients must satisfy the conditions:
1 * A + (-1) * B = 0, i.e. A = B.
Then the equation of a straight line has the form: Ax + Ay + C = 0, or x + y + C / A = 0.
at x=1, y=2 we get C/ A = -3, i.e. desired equation:
x + y - 3 = 0
Equation of a straight line in segments.
If in the general equation of the straight line Ah + Wu + C = 0 C≠0, then, dividing by -C, we get:
or , where
The geometric meaning of the coefficients is that the coefficient a is the coordinate of the intersection point
straight with axle Oh, a b- the coordinate of the point of intersection of the line with the axis OU.
Example. The general equation of a straight line is given x - y + 1 = 0. Find the equation of this straight line in segments.
C \u003d 1, , a \u003d -1, b \u003d 1.
Normal equation of a straight line.
If both sides of the equation Ah + Wu + C = 0 divide by number 
, which is called
normalizing factor, then we get
xcosφ + ysinφ - p = 0 -normal equation of a straight line.
The sign ± of the normalizing factor must be chosen so that μ * C< 0.
R- the length of the perpendicular dropped from the origin to the line,
a φ - the angle formed by this perpendicular with the positive direction of the axis Oh.
Example. Given the general equation of a straight line 12x - 5y - 65 = 0. Required to write various types of equations
this straight line.
The equation of this straight line in segments:
The equation of this line with slope: (divide by 5)
Equation of a straight line:
cos φ = 12/13; sin φ= -5/13; p=5.
It should be noted that not every straight line can be represented by an equation in segments, for example, straight lines,
parallel to the axes or passing through the origin.
Angle between lines on a plane.
Definition. If two lines are given y \u003d k 1 x + b 1, y \u003d k 2 x + b 2, then the acute angle between these lines
will be defined as
Two lines are parallel if k 1 = k 2. Two lines are perpendicular
if k 1 \u003d -1 / k 2 .
Theorem.
Direct Ah + Wu + C = 0 and A 1 x + B 1 y + C 1 \u003d 0 are parallel when the coefficients are proportional
A 1 \u003d λA, B 1 \u003d λB. If also С 1 \u003d λС, then the lines coincide. Coordinates of the point of intersection of two lines
are found as a solution to the system of equations of these lines.
The equation of a line passing through a given point is perpendicular to a given line.
Definition. A line passing through a point M 1 (x 1, y 1) and perpendicular to the line y = kx + b
represented by the equation:
The distance from a point to a line.
Theorem. If a point is given M(x 0, y 0), then the distance to the line Ah + Wu + C = 0 defined as:
Proof. Let the point M 1 (x 1, y 1)- the base of the perpendicular dropped from the point M for a given
direct. Then the distance between the points M and M 1:
(1)
Coordinates x 1 and 1 can be found as a solution to the system of equations:
The second equation of the system is the equation of a straight line passing through a given point M 0 perpendicularly
given line. If we transform the first equation of the system to the form:
A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,
then, solving, we get:
Substituting these expressions into equation (1), we find:
The theorem has been proven.
