Application of factorization of polynomials. "application of different methods of factoring a polynomial" Application of different methods of factoring
LESSON OUTLINE
Lesson type : a lesson in learning new material based on problem learning9 Purpose of the lesson
create conditions for practicing the skills and abilities of factoring the polynomial using various methods.
10. Objectives:
Educational
repeat the algorithms of operations: taking the common factor out of the bracket, grouping method, abbreviated multiplication formulas.
form the skill:
– apply knowledge on the topic of "factoring a polynomial into factors in various ways";
– perform tasks according to the chosen method of action;
– choose the most rational way to rationalize computations, transform polynomials.
Developing
to promote the development of cognitive abilities, attention, memory, thinking of students through the use of various exercises;
develop skills for independent work and group work; maintain students' interest in mathematics
Upbringing
maintain students' interest in mathematics
11.Formable UUD
Personal: awareness of the goal of the activity (expected result), awareness or choice of the method of activity (How will I do this? How will I get the result?), analysis and evaluation of the result; assessment of their capabilities;
Regulatory: take into account the rule in planning and controlling the way of solving, planning, evaluating the results of work;
Cognitive: choosing the most effective ways to solve problems, structuring knowledge; transformation of information from one type to another.
Communicative: planningeducational cooperation with the teacher and peers, adherence to the rules of speech behavior, the ability to express andjustify their point of view, take into account different opinions and strive to coordinate different positions in cooperation.
12.Methods:
by sources of knowledge: verbal, visual;
regarding the nature of cognitive activity: reproductive, partially exploratory.
13.Forms of work of students: frontal, individual, group.
14. Necessary Technical equipment: computer, projector, interactive whiteboard, handouts (self-control sheet, cards with tasks), electronic presentation made in the programPowerPoint
15.Planned results :
Personal fostering a sense of self and mutual respect; development of collaboration when working in groups;
Metasubject development of speech; development of students' independence; developing attentiveness when looking for errors.
Subject development of skills to work with information, mastery of solutions
During the classes:
1. Greetings from students. The teacher checks the readiness of the class for the lesson; organization of attention; instruction on how to work with the assessment sheetAttachment 1 , specification of evaluation criteria.
Checking homework and updating knowledge
1.3a + 6b \u003d 3 (a + 2b)2.100 - 20s + s 2 \u003d (10 + s) 2
3.s 2 - 81 \u003d (s - 9) (s + 9)
4.6x 3 - 5x 4 \u003d x 4 (6x - 5)
5.ay - 3y - 4a + 12 \u003d y (a - 3) - 4 (a - 3)
6.09x 2 - 0.25u 2 \u003d (0.03x - 0.05y) (0.03x + 0.05y)
7.s (x - 3) -d(x - 3) \u003d (x - 3) (c -d)
8.14x 2 - 7x \u003d 7x (7x - 1)
9.-1600 + a 12 \u003d (40 + a 6 ) (40 - a 6 )
10.9x 2 - 24hu + 16y 2 \u003d (3x - 4y) 2
11.8s 3 - 2s 2 + 4s - 1 \u003d
2c 2 (4s - 1) + (4s - 1) \u003d (4s - 1) 2s 2
12. b 4 + with 2 – 2 b 2 c \u003d (b – c) 2
(assignments for homework are taken from the textbook, include factoring in different ways. In order to complete this work, students need to remember previously studied material)
The answers written on the slide contain errors, students learn to see ways, and also, noticing mistakes, remember ways of action,
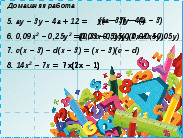

Students in groups, after checking their homework, assign points for the work done
2 RelayAppendix 2 (team members take turns completing the task, while using an arrow they connect the example and the method of its decomposition)
3a - 12b \u003d 3 (a - 4 b)2a + 2b + a 2 + ab \u003d (a + b) (2 + a)
9a 2 - 16b 2 = ( 3a - 4 b) (3a + 4b)
16a 2 - 8ab + b 2 \u003d (4а - b) 2
7a 2 b - 14ab 2 + 7ab \u003d 7ab (a - 2b + 1)
a 2 + ab- a - ac- bc + c \u003d (a + b - 1) (a - c)
25a 2 + 70ab + 49b 2 = ( 5a + 7 b) 2
5x 2 - 45u 2 \u003d 5 (x - 3y) (x + 3y)
![]()
Does not factorize
Grouping method

The slide is used to check the work done, while paying attention to the fact that the last example needs to be combined with two methods of expansion (parenthesis of the common factor and the formula for reduced multiplication)
Students evaluate the work done, enter the results on the assessment sheets, and also formulate the topic of the lesson

3. Completion of assignments (students are invited to complete the assignment. Discussing the solution in the group, the children come to the conclusion that it takes several ways to factorize these polynomials. The team that first proposes the correct decomposition has the right to write down its solution on the board, the rest write it down in a notebook .. The team has established a work to help students who find it difficult to cope with the task)
1) 2a 2 - 2b 25) 5m 2 + 5n 2 - 10mn
9) 84 - 42y - 7xy + 14x
13) x 2 y + 14xy 2 + 49y 3
2) 3a 2 + 6ab + 3b 2
6) cx 2 - cy 2
10) -7b 2 - 14bc - 7c 2
14) 3ab 2 - 27a
3) x 3 - 4x
7) -3x 2 + 12x - 12
11) 3x 2 - 3
15) -8a 3 b + 56a 2 b 2 - 98ab 3
4) 3ab + 15b - 3a - 15
8) x 4 - x 2
12) c 4 - 81
16) 0 , 09t 4 - t 6
4. The final stage -Factoring a polynomial
Taking the common factor out of parentheses
Grouping method
Abbreviated multiplication formula
Lesson summary. Students answer questions: What task did we set? Did we manage to solve the task at hand? How? What are the results? In what ways is a polynomial factorized? What tasks can this knowledge be applied to? What did you do well in the lesson? What else needs to be worked on?
During the lesson, the students assessed themselves, at the end of the lesson they are asked to add up the points they received and give a grade in accordance with the proposed scale.
The final word of the teacher: Today in the lesson we learned to determine what methods should be used to factor polynomials. To consolidate the work done
Homework: §19, no. 708, no. 710
Additional task:
Solve the equation x 3 + 4x 2 \u003d 9x + 36
- Formation of skills to apply various methods for factoring.
- Contribute to the education of a culture of speech, accuracy of writing, independence.
- Formation of skills in partial search activity: to understand the problem, analyze, draw conclusions.
Equipment: textbook, blackboard, notebook, cards with assignments.
Lesson type: Lesson in the use of ZUN.
Teaching method: problematic, partially exploratory.
Form of organization of educational activities: group, frontal, individual, work in pairs.
Duration: 1 lesson (45 min)
Lesson plan:
- Organization of the beginning of the lesson. (1 min)
- Homework check. (2 minutes)
- Updating. (5 minutes)
- Learning new material. (10 minutes)
- Securing new material. (15 minutes)
- Control and self-examination of knowledge. (8 minutes)
- Summarizing. (2 minutes)
- Homework. (2 minutes)
During the classes
I. Organizational moment
Hello guys.
The topic of the lesson is "Using different methods for factoring." Today we will be with you to form the skills of using various methods of factoring and once again we will be convinced of the usefulness of the ability to factor a polynomial.
I wish you to work actively in the lesson. (Write the topic in a notebook).
II. Homework check
Before the start of the lesson, students submit notebooks with completed homework for review. The issues that caused difficulties are discussed.
III. Updating basic knowledge.
Before we start solving problems, let's check how ready we are for this. Let's remember what we know on the topic of the lesson.
3.1. Frontal poll:
a) What does it mean to factor a polynomial?
b) What are the main methods of factoring a polynomial into factors do you know?
c) Any polynomial can be factorized? For instance?
d) In what tasks is it sometimes useful to use factorization?
3.2. Connect the polynomials with their corresponding factorization methods by lines.

3.3. Find the wrong statement:
a) a 2 + b 2 - 2ab \u003d (a - b) 2
b) m 2 + 2mn - n 2 \u003d (m - n) 2
c) –2pt + p 2 + t 2 \u003d (p - t) 2
d) 25 - 16 s 2 \u003d (5 - 4s) (5 - 4s) (errors b, d)
3.4. Present as a work:a) 64x 2 - 1; b) (d - 3) 2 - 36;
3.5. Solve the equation x 2 - 16 \u003d 0 (4; –4)
3.5. Find the value of an expression 34 2 – 24 2 (580)
IV. Study of the material
To factorize polynomials, we used parentheses, grouping, and abbreviated multiplication formulas.
Do you think there are situations in which it is possible to factor a polynomial using several methods sequentially?
The following task will help us find the answer to this question:
Factor the polynomial and indicate which methods were used. ( Work in pairs followed by a decision at the board)
Example 1.9x 3 - 36x used 2 methods:
Example 2.a 2 + 2ab + b 2 - c 2 applied 2 methods:
- grouping;
- use of abbreviated multiplication formulas.
Example 3.y 3 - 3y 2 + 6y - 18 applied 3 methods:
- grouping;
- use of abbreviated multiplication formulas;
- taking the common factor out of the parentheses.
Example 4.x 3 + 3x 2 + 2x applied 3 methods:
- taking the common factor out of parentheses;
- preliminary conversion;
- grouping.
We conclude: sometimes it is possible to factor out a polynomial by applying several methods in succession. To successfully tackle these examples, today let's develop a plan for consistently applying them:
- Factor out the common factor (if any).
- Try to factorize the polynomial using the abbreviated multiplication formulas.
- Try to apply the grouping method (if the previous methods did not lead to the goal).
V. Exercises to consolidate the stated topic
5.1. The combination of various methods of factorization allows you to easily and gracefully perform arithmetic calculations, solve equations of the form ax 2 + bx + c \u003d 0 (a ≠ 0) (such equations are called quadratic, we will study them in grade 8).
* Solve the equation: a) x 2 - 17x + 72 \u003d 0, b) x 2 + 10x + 21 \u003d 0
Hint: Some term of the polynomial is decomposed into necessary terms or supplemented by adding some term to it. In the latter case, so that the polynomial does not change, the same term is subtracted from it.
(Two students solve equations independently in a notebook. Answer: a) 8; 9; b) - 1; - five).
Perform the exercise from textbook No. 1016 (c), 1017 (c), page 186
(Two students solve on the blackboard, the rest according to the options in the notebook).
5.2. Solve equations ( Students work in pairs followed by self-examination)
No. 949, page 177 a) x 3 - x \u003d 0 b) 9x - x 3 \u003d 0 c) x 3 + x 2 \u003d 0 d) 5x 4 - 2x 2 \u003d 0
** (Individual assignments for more prepared students)
| Card 1 | Card 2 | Card 3 |
| Solve the equation and indicate the sum of the roots x 2 + 3x + 6 + 2x \u003d 0 |
Solve the equation and indicate the sum of the roots |
| x (x + 3) +2 (3 + x) \u003d 0 sum is -5 |
The sum of the roots of this equation: |
 The sum of the roots of the equation: |
Vi. Control and self-examination of knowledge.
The topic under consideration is an integral part of the GIA in mathematics. To control and self-test knowledge on this topic, you are invited to complete test tasks from the training tasks of the GIA. Circle the answer in the test items.
Individual work on cards: (Students complete the GIA test tasks, + self-test)
Which of these expressions are identically equal to 4x-10y
a) 1; 3; b) everything; c) 1; 2; 4; oppression |
Which of these expressions are identically equal - 3 (-2a + y)
and all; b) 2; y) 2; 3; c) 1; 4 |
Which of these expressions are identically equal to -6a + 12p
a) 1; at all; c) 2; 4; d) 1; 3 |
| 3a 3 -3a 2 -5a + 5. a) (a-1) (3a 2 +5); b) (a + 1) (3a 2 -5); c) (a-1) (5-3a 2); f) (a-1) (3a 2 +5). |
Represent as a product of polynomials 13ax-26x-5av + 10v. e) (a-2) (13x-5c); b) (a + 2) (3x-5c); c) (3a-6) (4x-c); d) (a-2) (5c-3x). |
Represent as a product of polynomials bу-6b-5y 2 + 30y. a) (6-y) (b-5y); b) (y -6) (b + 5y); c) (y -6) (b-5y); d) (y -6) (5y-b). |
| Perform steps: (5a-c) 2. a) 25a 2 + 10ac + s 2; b) 25a 2 + 10ac-s 2; p) 25a 2 -10ac + c 2; d) 25a 2 -5ac + s 2. |
Follow the steps: (5x + 2y) 2. a) 25x 2 + 20xy + 4y 2; success |
Teacher: Let's check the answers. Read the words you get. These are exactly the words that accompany seventh graders in preparation for the GIA in the 9th grade.
Vii. Lesson summary
The teacher conducts a frontal review of the main stages of the lesson, assesses the work of the students and guides the students in their homework.
VIII. Homework:p. 38, No. 950 (p. 177), No. 1016 (g), 1017 (g), p. 186.
** Find the value of the expression (x + 3) 2 -2 (x + 3) (x-3) + (x-3) 2 at x \u003d 100.
The value of this expression does not depend on the choice of x.
The lesson is over. Thank you for the lesson and remember that knowledge that is not replenished daily decreases every day.
Used Books:
- Textbook "Algebra Grade 7". Yu.N. Makarychev, N.G. Mindyuk et al. Ed. S.A. Telyakovsky. - M .; Enlightenment, 2009.
- Collection of test items for thematic and final control. Algebra 7.I.L. Gusev and others - M .; Intellect Center, 2009.
- State final certification (in a new form): Grade 9. Thematic training tasks. Algebra / FIPI author-compiler: V.L. Kuznetsova. - M .: Eksmo, 2010.
Polynomials are the most important type of mathematical expression. On the basis of polynomials, a lot of equations, inequalities, functions are constructed. Problems of various levels of complexity often contain stages of a versatile transformation of polynomials. Since mathematically any polynomial is an algebraic sum of several monomials, the most radical and necessary change is the transformation of a series of polynomials into the product of two (or more) factors. In equations that have the ability to zero one of the parts, translating the polynomial into factors allows one to equate some part to zero, and thus solve the entire equation.
Previous video tutorials have shown us that there are three main ways to convert polynomials to factors in linear algebra. This is the removal of the common factor from the brackets, the regrouping by similar terms, the application of the abbreviated multiplication formulas. If all the terms of the polynomial have some common base, then it can easily be taken out of the brackets, leaving the remainders from divisions in the form of a modified polynomial in brackets. But more often than not, one factor does not fit all monomials, affecting only a part of them. At the same time, the other part of monomials can have their own common basis. In such cases, the grouping method is used - in fact, bracketing several factors, and creating a complex expression that can be transformed in other ways. And finally, there is a whole range of special formulas. All of them are formed by abstract calculations using the method of the simplest term-by-term multiplication. During the calculations, many elements in the initial expression are canceled, leaving small polynomials. In order not to carry out capacious calculations every time, you can use ready-made formulas, their reverse versions, or generalized conclusions of these formulas.

In practice, it often happens that in one exercise you have to combine several techniques, including those from the category of transforming polynomials. Let's look at an example. Factor with binomial:
Factor out the common factor of 3x:
3x3 - 3xy2 \u003d 3x (x2 - y2)
As you can see in the video, the second brackets contain the difference of the squares. We apply the inverse formula for reduced multiplication, getting:
3x (x2 - y2) \u003d 3x (x + y) (x - y)
Another example. We transform an expression of the form:
18a2 - 48a + 32
We decrease the numerical coefficients, taking out the two from the brackets:
18a2 - 48a + 32 \u003d 2 (9a2 - 24a + 16)

In order to find a suitable formula for abbreviated multiplication for this case, it is necessary to slightly correct the expression, adjusting it to the conditions of the formula:
2 (9a2 - 24a + 16) \u003d 2 ((3a) 2 - 2 (3a) 4 + (4) 2)
Sometimes it is not so easy to see the formula in confusing terms. You have to use methods of decomposing an expression into its constituent elements, or add imaginary pairs of constructions, such as + x-x. When correcting an expression, we must observe the rules of the continuity of signs, and the preservation of the meaning of the expression. At the same time, you need to try to bring the polynomial to full compliance with the abstract version of the formula. For our example, we apply the formula for the square of the difference:
2 ((3а) 2 - 2 (3а) 4 + (4) 2) \u003d 2 (3а - 4)
Let's solve a more difficult exercise. Let us factorize the polynomial:
Y3 - 3y2 + 6y - 8
To begin with, let's make a convenient grouping - the first and fourth elements into one group, the second and third into the second:
Y3 - 3y2 + 6y - 8 \u003d (y3 - 8) - (3y2 - 6y)
Note that the signs in the second parentheses have changed to the opposite, since we have moved the minus outside the expression. In the first brackets we can write like this:
(y3 - (2) 3) - (3y2 - 6y)
This allows you to apply the abbreviated multiplication formula to find the difference between cubes:
(y3 - (2) 3) - (3y2 - 6y) \u003d (y - 2) (y2 + 2y + 4) - (3y2 - 6y)

We take out the common factor 3y from the second brackets, after which we take out the brackets (y - 2) from the entire expression (binomial), we give similar terms:
(y - 2) (y2 + 2y + 4) - (3y2 - 6y) \u003d (y - 2) (y2 + 2y + 4) - 3y (y - 2) \u003d
\u003d (y - 2) (y2 + 2y + 4 - 3y) \u003d (y - 2) (y2 - y + 4)
In a general approximation, there is a certain algorithm of actions when solving such exercises.
1. We are looking for common factors for the entire expression;
2. We group similar monomials, looking for common factors for them;
3. We try to put out the brackets the most suitable expression;
4. We apply the formulas for reduced multiplication;
5. If at some stage the process does not go - we enter an imaginary pair of expressions of the form -x + x, or other self-canceling constructions;
6. We give similar terms, reduce unnecessary elements
All points of the algorithm are rarely applicable in one task, but the general course of solving any exercise on the topic can be followed in a given order.
The purpose of the lesson: the formation of the skills of decomposing a polynomial into factors in various ways; educate accuracy, perseverance, hard work, the ability to work in pairs. Equipment: multimedia projector, PC, didactic materials. Lesson plan: 1. Organizational moment; 2. Checking homework; 3. Oral work; 4. Learning new material; 5. Physical education; 6. Consolidation of the studied material; 7. Work in pairs; 8. Homework; 9. Summing up. Lesson course: 1. Organizational moment. Direct students to the lesson. Education does not consist in the amount of knowledge, but in the full understanding and skillful application of everything that you know. (Georg Hegel) 2. Checking homework. Analysis of tasks, in solving which students have difficulties. 3. Oral work. factor into factors: 1) 2) 3); four) . Match the left and right column expressions: a. 1. b. 2.c. 3. d. 4. d. 5.. Solve the equations: 1. 2. 3. 4. Learning new material. To factorize polynomials, we used parentheses, grouping, and abbreviated multiplication formulas. Sometimes it is possible to factor out a polynomial using several methods in succession. The conversion should begin, if possible, by taking the common factor outside the brackets. To successfully address such examples, today we will try to develop a plan for their consistent application.
150,000 rubles prize fund 11 honorary documents Certificate of publication in the media
This is one of the most basic ways to simplify expression. To apply this method, let's remember the distributional law of multiplication relative to addition (don't be intimidated by these words, you definitely know this law, you just might have forgotten its name).
The law says: in order to multiply the sum of two numbers by the third number, you need to multiply each term by this number and add the results obtained, in other words,.
You can also do the reverse operation, and it is this reverse operation that interests us. As you can see from the sample, the common factor a can be taken out of the bracket.
A similar operation can be done both with variables, such as and, for example, and with numbers:.
Yes, this is too elementary an example, just like the above example, with the expansion of a number, because everyone knows that numbers are divisible by, but what if you got a more complicated expression:
How do you know what, for example, a number is divided by, nooo, with a calculator, anyone can, but without it, it's weak? And for this there are divisibility criteria, these signs are really worth knowing, they will help you quickly understand whether it is possible to factor out the common factor.
Divisibility criteria
Remembering them is not so difficult, most likely, most of them were already familiar to you, but something will be a new useful discovery, more details in the table:
Note: The table is missing a divisibility by 4 criterion. If the last two digits are divisible by 4, then the whole number is divisible by 4.
How do you like the sign? I advise you to remember it!
Well, back to the expression, can take it out of the bracket and that's enough from it? No, it is customary for mathematicians to simplify, so to the full, take out EVERYTHING that is taken out!
And so, everything is clear with the game, but what about the numerical part of the expression? Both numbers are odd, so you can't divide by,
You can use the divisibility sign by, the sum of the digits, and, of which the number consists, is equal, and is divided by, which means it is divided by.
Knowing this, you can safely divide in a column, as a result of dividing by we get (the divisibility criteria came in handy!). Thus, we can put the number outside the bracket, just like y and as a result we have:
To make sure that everything is decomposed correctly, you can check the decomposition, multiplication!
Also, the common factor can be taken out in power expressions. Here, for example, do you see the common factor?
All members of this expression have x's - we take out, everything is divided into - we take out again, see what happened:.
2. Formulas for abbreviated multiplication
Abbreviated multiplication formulas have already been mentioned in theory, if you hardly remember what it is, then you should brush it up again.
Well, if you consider yourself very smart and you are too lazy to read such a cloud of information, then just read on, take a look at the formulas and immediately take examples.
The essence of this decomposition is to notice in the expression in front of you some definite formula, apply it and thus obtain the product of something and something, that's all the decomposition. The following are the formulas:
Now try factoring the following expressions using the formulas above:
And here's what should have happened:
As you have noticed, these formulas are a very effective way of factoring, they are not always suitable, but they can be very useful!
3. Grouping or grouping method
And here's another example for you:
well, what are you going to do with him? It seems to be divided into something and into, and something into and into
But you can't divide everything together into one thing, well there is no common factor, how not to look for what, and leave without factoring?
Here you need to show your ingenuity, and the name of this ingenuity is a group!
It is used just when not all members have common divisors. For grouping you need find groups of terms having common divisors and rearrange them so that the same multiplier can be obtained from each group.
Of course, it is not necessary to rearrange in places, but it gives clarity, for clarity, you can put individual parts of the expression in brackets, it is not forbidden to put them as much as you like, the main thing is not to confuse the signs.
Not very clear about all this? Let me explain with an example:
In the polynomial - we put the term - after the term - we get
we group the first two terms together in a separate parenthesis and also group the third and fourth terms, taking the minus sign outside the parenthesis, we get:
And now we look separately at each of the two "heaps" into which we split the expression with parentheses.
The trick is to break into such piles from which you can take out the largest factor possible, or, as in this example, try to group the terms so that after removing the factors from the piles of factors from the bracket, we have the same expressions inside the parentheses.
From both brackets we take out the common factors of the terms from the brackets, from the first bracket, and from the second, we get:
But this is not decomposition!
Pdonkey expansion, only multiplication should remain, but for now, the polynomial is simply divided into two parts ...
BUT! This polynomial has a common factor. it
brackets and get the final product
Bingo! As you can see, there is already a product and there is no addition or subtraction outside the brackets, the decomposition is complete, because we have nothing more to take out of the brackets.
It may seem like a miracle that after putting the factors outside the brackets, we still have the same expressions in the brackets, which we again put outside the brackets.
And this is not a miracle at all, the fact is that the examples in textbooks and in the exam are specially made so that most expressions in tasks for simplification or factorization with the right approach to them, they are easily simplified and sharply collapsed like an umbrella when you press a button, so look for that very button in each expression.
Something I digress, what do we have there with the simplification? The intricate polynomial took on a simpler form:.
Agree, not as bulky as it was?
4. Selecting a complete square.
Sometimes, to apply the formulas for reduced multiplication (repeat the topic), it is necessary to transform the existing polynomial, presenting one of its terms as the sum or difference of two terms.
In which case you have to do this, you learn from the example:
A polynomial in this form cannot be decomposed using abbreviated multiplication formulas, so it must be transformed. Perhaps at first it will not be obvious to you which term to break into which, but over time you will learn to immediately see the abbreviated multiplication formulas, even if they are not completely present, and you will quickly determine what is missing here to complete the formula, but for now - learn , a student, or rather a schoolboy.
For a complete formula, the square of the difference is needed instead of. We represent the third term as a difference, we get: The formula for the square of the difference can be applied to the expression in brackets (not to be confused with the difference of squares !!!), we have:, to this expression you can apply the formula for the difference of squares (not to be confused with the square of the difference !!!), presenting how, we get:.
An expression decomposed into factors does not always look simpler and smaller than it was before the decomposition, but in this form it becomes more mobile, in the sense that you can not worry about changing signs and other mathematical nonsense. Well, here for you for an independent solution, the following expressions need to be factorized.
Examples:
Answers:
5. Factoring a square trinomial
For the factorization of a square trinomial, see further decomposition examples.
Examples of 5 methods for factoring a polynomial
1. Taking the common factor out of the brackets. Examples.
Do you remember what a distribution law is? This is the rule:
Example:
Factor a polynomial.
Decision:
Another example:
Factor.
Decision:
If the term is completely outside the brackets, the unit is left in the brackets instead!
2. Formulas for abbreviated multiplication. Examples.
Most often we use the formulas difference of squares, difference of cubes and sum of cubes. Do you remember these formulas? If not, urgently repeat the topic!
Example:
Factor the expression.
Decision:
In this expression, it is easy to find out the difference between the cubes:
Example:
Decision:
3. Grouping method. Examples of
Sometimes it is possible to swap the terms in such a way that the same factor can be selected from each pair of adjacent terms. This common factor can be taken out of the bracket and the original polynomial will turn into a product.
Example:
Factor a polynomial.
Decision:
We group the terms as follows:
.
In the first group we take out the common factor outside the bracket, and in the second -:
.
Now the common factor can also be taken out of the brackets:
.
4. The method of highlighting a complete square. Examples.
If the polynomial can be represented as the difference of the squares of two expressions, all that remains is to apply the formula of abbreviated multiplication (difference of squares).
Example:
Factor a polynomial.
Decision:Example:
\\ begin (array) (* (35) (l))
((x) ^ (2)) + 6 (x) -7 \u003d \\ underbrace (((x) ^ (2)) + 2 \\ cdot 3 \\ cdot x + 9) _ (square \\ sum \\ ((\\ left (x + 3 \\ right)) ^ (2))) - 9-7 \u003d ((\\ left (x + 3 \\ right)) ^ (2)) - 16 \u003d \\\\
\u003d \\ left (x + 3 + 4 \\ right) \\ left (x + 3-4 \\ right) \u003d \\ left (x + 7 \\ right) \\ left (x-1 \\ right) \\\\
\\ end (array)
Factor a polynomial.
Decision:
\\ begin (array) (* (35) (l))
((x) ^ (4)) - 4 ((x) ^ (2)) - 1 \u003d \\ underbrace (((x) ^ (4)) - 2 \\ cdot 2 \\ cdot ((x) ^ (2) ) +4) _ (square \\ difference ((\\ left (((x) ^ (2)) - 2 \\ right)) ^ (2))) - 4-1 \u003d ((\\ left (((x) ^ (2)) - 2 \\ right)) ^ (2)) - 5 \u003d \\\\
\u003d \\ left (((x) ^ (2)) - 2+ \\ sqrt (5) \\ right) \\ left (((x) ^ (2)) - 2- \\ sqrt (5) \\ right) \\\\
\\ end (array)
5. Factorization of a square trinomial. Example.
A square trinomial is a polynomial of the form, where is the unknown, are some numbers, and.
The values \u200b\u200bof a variable that turn a square trinomial to zero are called trinomial roots. Therefore, the roots of the trinomial are the roots of the quadratic equation.
Theorem.
Example:
Let's factorize the square trinomial:.
First, we solve the quadratic equation: Now you can write the factorization of this quadratic trinomial:
Now your opinion ...
We have described in detail how and why to factor out a polynomial.
We gave a lot of examples of how to do this in practice, pointed out the pitfalls, gave solutions ...
What do you say?
How do you like this article? Do you use these techniques? Do you understand their essence?
Write in the comments and ... get ready for the exam!
So far, he is the most important in your life.







