How to pronounce abbreviated multiplication formulas. Abbreviated multiplication formulas

>> Mathematics: Abbreviated Multiplication Formulas

Abbreviated multiplication formulas

There are several cases where the multiplication of one polynomial by another leads to a compact, easy-to-remember result. In these cases, it is preferable not to multiply each time by one polynomial on the other, but use the finished result. Let's consider these cases.

1. The square of the sum and the square of the difference:

Example 1. Expand parentheses in expression:

a) (Zx + 2) 2;

b) (5а 2 - 4b 3) 2

a) We use formula (1), taking into account that Zx plays the role of a, and the number 2 plays the role of b.
We get:

(Zx + 2) 2 = (Zx) 2 + 2 Zx 2 + 2 2 = 9x 2 + 12x + 4.

b) We use the formula (2) considering that in the role a advocates 5a 2, and in the role b advocates 4b 3... We get:

(5a 2 -4b 3) 2 = (5a 2) 2 - 2- 5a 2 4b 3 + (4b 3) 2 = 25a 4 -40a 2 b 3 + 16b 6.

When using the squared sum or squared difference formulas, keep in mind that
(- a - b) 2 = (a + b) 2;
(b-a) 2 = (a-b) 2.

This follows from the fact that (- a) 2 = a 2.

Note that some mathematical tricks are based on formulas (1) and (2), allowing you to make calculations in your head.

For example, you can almost orally square numbers ending in 1 and 9. Indeed

71 2 = (70 + 1) 2 = 70 2 + 2 70 1 + 1 2 = 4900 + 140 + 1 = 5041;
91 2 = (90 + I) 2 = 90 2 + 2 90 1 + 1 2 = 8100 + 180 + 1 = 8281;
69 2 = (70 - I) 2 = 70 2 - 2 70 1 + 1 2 = 4900 - 140 + 1 = 4761.

Sometimes you can quickly square a number ending in the number 2 or the number 8. For example,

102 2 = (100 + 2) 2 = 100 2 + 2 100 2 + 2 2 = 10 000 + 400 + 4 = 10 404;

48 2 = (50 - 2) 2 = 50 2 - 2 50 2 + 2 2 = 2500 - 200 + 4 = 2304.

But the most elegant trick involves squaring numbers ending in 5.
Let us carry out the corresponding reasoning for 85 2.

We have:

85 2 = (80 + 5) 2 = 80 2 + 2 80 5 + 5 2 =-80 (80+ 10)+ 25 = 80 90 + 25 = 7200 + 25 = 7225.

Note that to calculate 85 2 it was enough to multiply 8 by 9 and assign 25 to the right of the result. The same can be done in other cases. For example, 35 2 = 1225 (3 4 = 12 and 25 was added to the resulting number on the right);

65 2 = 4225; 1252 = 15625 (12 18 = 156 and 25 was added to the resulting number on the right).

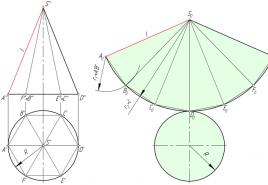
Since we are talking about various curious circumstances associated with boring (at first glance) formulas (1) and (2), then we will supplement this conversation with the following geometric reasoning. Let a and b be positive numbers. Consider a square with sides a + b and cut out in two of its corners squares with sides equal to a and b, respectively (Fig. 4).

The area of ​​a square with side a + b is (a + b) 2. But we cut this square into four parts: a square with side a (its area is a 2), a square with side b (its area is b 2), two rectangles with sides a and b (the area of ​​each such rectangle is ab). Hence, (a + b) 2 = a 2 + b 2 + 2ab, that is, we obtained formula (1).

Multiply the binomial a + b by the binomial a - b. We get:
(a + b) (a - b) = a 2 - ab + bа - b 2 = a 2 - b 2.
so

Any equality in mathematics is used both from left to right (that is, the left side of the equality is replaced by its right side), and from right to left (that is, the right side of the equality is replaced by its left side). If formula C) is used from left to right, then it allows you to replace the product (a + b) (a - b) with the finished result a 2 - b 2. The same formula can be used from right to left, then it allows you to replace the difference of squares a 2 - b 2 by the product (a + b) (a - b). Formula (3) in mathematics is given a special name - the difference of squares.

Comment. Do not confuse the terms "difference of squares" k and "square of the difference". The difference of the squares is a 2 - b 2, which means that we are talking about the formula (3); the square of the difference is (a - b) 2, which means we are talking about the formula (2). In ordinary language, formula (3) is read "from right to left" as follows:

the difference of the squares of two numbers (expressions) is equal to the product of the sum of these numbers (expressions) by their difference,

Example 2. Perform multiplication

(3x- 2y) (3x + 2y)
Solution. We have:
(Zx - 2y) (Zx + 2y) = (Zx) 2 - (2y) 2 = 9x 2 - 4y 2.

Example 3. Represent a 16x 4 - 9 binomial as a product of binomials.

Solution. We have: 16x 4 = (4x 2) 2, 9 = З 2, which means that the given binomial is the difference of squares, i.e. formula (3), read from right to left, can be applied to it. Then we get:

16x 4 - 9 = (4x 2) 2 - З 2 = (4x 2 + 3) (4x 2 - 3)

Formula (3), like formulas (1) and (2), is used for mathematical tricks. See:

79 81 = (80 - 1) (80 + 1) - 802 - I2 = 6400 - 1 = 6399;
42 38 = D0 + 2) D0 - 2) = 402 - 22 = 1600 - 4 = 1596.

Let's conclude our conversation about the formula for the difference of squares with an interesting geometric reasoning. Let a and b be positive numbers, with a> b. Consider a rectangle with sides a + b and a - b (Fig. 5). Its area is (a + b) (a - b). Cut off a rectangle with sides b and a - b and glue it to the rest of the part as shown in Figure 6. It is clear that the resulting figure has the same area, ie (a + b) (a - b). But this figure can be
build like this: from a square with side a, cut a square with side b (this is clearly seen in Fig. 6). Hence, the area of ​​the new figure is equal to a 2 - b 2. So, (a + b) (a - b) = a 2 - b 2, that is, we got the formula (3).

3. Difference of cubes and sum of cubes

Multiply the binomial a - b by the trinomial a 2 + ab + b 2.
We get:
(a - b) (а 2 + ab + b 2) = а а 2 + а ab + а b 2 - b а 2 - b аb -bb 2 = а 3 + а 2 b + аb 2 -а 2 b- ab 2 -b 3 = a 3 -b 3.

Likewise

(a + b) (a 2 - ab + b 2) = a 3 + b 3

(check it yourself). So,

Formula (4) is usually called difference of cubes, formula (5) is the sum of cubes. Let's try to translate formulas (4) and (5) into ordinary language. Before doing this, note that the expression a 2 + ab + b 2 is similar to the expression a 2 + 2ab + b 2, which appeared in formula (1) and gave (a + b) 2; the expression a 2 - ab + b 2 is similar to the expression a 2 - 2ab + b 2, which appeared in formula (2) and gave (a - b) 2.

To distinguish (in language) these pairs of expressions from each other, each of the expressions a 2 + 2ab + b 2 and a 2 - 2ab + b 2 is called a perfect square (sum or difference), and each of the expressions a 2 + ab + b 2 and a 2 - ab + b 2 are called an incomplete square (sum or difference). Then the following translation of formulas (4) and (5) (read "from right to left") into ordinary language is obtained:

the difference between the cubes of two numbers (expressions) is equal to the product of the difference between these numbers (expressions) and the incomplete square of their sum; the sum of cubes of two numbers (expressions) is equal to the product of the sum of these numbers (expressions) by the incomplete square of their difference.

Comment. All formulas (1) - (5) obtained in this section are used both from left to right and from right to left, only in the first case (from left to right) they say that (1) - (5) are abbreviated multiplication formulas, and in the second case (from right to left) say that (1) - (5) are factorization formulas.

Example 4. Perform multiplication (2x- 1) (4x 2 + 2x +1).

Solution. Since the first factor is the difference between the monomials 2x and 1, and the second factor is the incomplete square of their sum, you can use formula (4). We get:

(2x - 1) (4x 2 + 2x + 1) = (2x) 3 - I 3 = 8x 3 - 1.

Example 5. Represent the binomial 27a 6 + 8b 3 as a product of polynomials.

Solution. We have: 27a 6 = (For 2) 3, 8b 3 = (2b) 3. This means that the given binomial is the sum of cubes, that is, formula 95) can be applied to it, read from right to left. Then we get:

27a 6 + 8b 3 = (For 2) 3 + (2b) 3 = (For 2 + 2b) ((For 2) 2 - For 2 2b + (2b) 2) = (For 2 + 2b) (9a 4 - 6a 2 b + 4b 2).

Help for the student online, Mathematics for grade 7 download, calendar-thematic planning

A. V. Pogorelov, Geometry for grades 7-11, Textbook for educational institutions

Lesson content lesson outline support frame lesson presentation accelerative methods interactive technologies Practice tasks and exercises self-test workshops, trainings, cases, quests home assignments discussion questions rhetorical questions from students Illustrations audio, video clips and multimedia photos, pictures, charts, tables, schemes humor, jokes, jokes, comics parables, sayings, crosswords, quotes Supplements abstracts articles chips for the curious cheat sheets textbooks basic and additional vocabulary of terms others Improving textbooks and lessonsbug fixes in the tutorial updating a fragment in the textbook elements of innovation in the lesson replacing obsolete knowledge with new ones For teachers only perfect lessons calendar plan for the year methodological recommendations of the discussion program Integrated lessons

Abbreviated Multiplication Formulas (ACF) are used for exponentiation and multiplication of numbers and expressions. Often these formulas allow you to make calculations more compact and faster.

In this article, we will list the basic formulas for abbreviated multiplication, group them in a table, consider examples of using these formulas, and also dwell on the principles of proof of abbreviated multiplication formulas.

For the first time, the topic of FSU is considered within the framework of the "Algebra" course for the 7th grade. Below are 7 basic formulas.

Abbreviated multiplication formulas

1. the formula for the square of the sum: a + b 2 = a 2 + 2 a b + b 2
2. the formula for the square of the difference: a - b 2 = a 2 - 2 a b + b 2
3. sum cube formula: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
4. difference cube formula: a - b 3 = a 3 - 3 a 2 b + 3 a b 2 - b 3
5. difference of squares formula: a 2 - b 2 = a - b a + b
6. the formula for the sum of cubes: a 3 + b 3 = a + b a 2 - a b + b 2
7. the formula for the difference of cubes: a 3 - b 3 = a - b a 2 + a b + b 2

The letters a, b, c in these expressions can be any numbers, variables or expressions. For ease of use, it is best to learn the seven basic formulas by heart. Let's summarize them in a table and present them below, encircling them with a frame.

The first four formulas allow you to calculate, respectively, the square or cube of the sum or difference of two expressions.

The fifth formula calculates the difference of the squares of the expressions by the product of their sum and the difference.

The sixth and seventh formulas are, respectively, the multiplication of the sum and difference of expressions by an incomplete square of the difference and an incomplete square of the sum.

The abbreviated multiplication formula is sometimes also called the abbreviated multiplication identities. This is not surprising, since every equality is an identity.

When solving practical examples, abbreviated multiplication formulas with rearranged left and right sides are often used. This is especially useful when a factorization of a polynomial takes place.

Additional abbreviated multiplication formulas

We will not limit ourselves to the 7th grade course in algebra and add a few more formulas to our FSU table.

First, consider the Newton binomial formula.

a + b n = C n 0 a n + C n 1 a n - 1 b + C n 2 a n - 2 b 2 +. ... + C n n - 1 a b n - 1 + C n n b n

Here C n k are binomial coefficients that are in row n in the pascal triangle. Binomial coefficients are calculated by the formula:

C n k = n! k! (N - k)! = n (n - 1) (n - 2). ... (n - (k - 1)) k!

As you can see, the FSE for the square and the cube of the difference and the sum is a special case of the Newton binomial formula for n = 2 and n = 3, respectively.

But what if there are more than two terms in the sum to be raised to the power? The formula for the square of the sum of three, four or more terms will be useful.

a 1 + a 2 +. ... + a n 2 = a 1 2 + a 2 2 +. ... + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 +. ... + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 +. ... + 2 a 2 a n + 2 a n - 1 a n

Another formula that may come in handy is the formula for the difference between the n-th powers of two terms.

a n - b n = a - b a n - 1 + a n - 2 b + a n - 3 b 2 +. ... + a 2 b n - 2 + b n - 1

This formula is usually divided into two formulas - for even and odd degrees, respectively.

For even indicators 2m:

a 2 m - b 2 m = a 2 - b 2 a 2 m - 2 + a 2 m - 4 b 2 + a 2 m - 6 b 4 +. ... + b 2 m - 2

For odd exponents 2m + 1:

a 2 m + 1 - b 2 m + 1 = a 2 - b 2 a 2 m + a 2 m - 1 b + a 2 m - 2 b 2 +. ... + b 2 m

The formulas for the difference of squares and the difference of cubes, you guessed it, are special cases of this formula for n = 2 and n = 3, respectively. For the difference of cubes, b is also replaced with - b.

How to read abbreviated multiplication formulas?

We will give the appropriate formulations for each formula, but first we will understand the principle of reading formulas. The most convenient way to do this is by example. Let's take the very first formula for the square of the sum of two numbers.

a + b 2 = a 2 + 2 a b + b 2.

They say: the square of the sum of two expressions a and b is equal to the sum of the square of the first expression, the doubled product of the expressions and the square of the second expression.

All other formulas are read in the same way. For the square of the difference a - b 2 = a 2 - 2 a b + b 2 we write:

the square of the difference between the two expressions a and b is equal to the sum of the squares of these expressions minus twice the product of the first and second expressions.

Read the formula a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3. The cube of the sum of two expressions a and b is equal to the sum of the cubes of these expressions, three times the square of the first expression by the second, and three times the square of the second expression by the first expression.

We proceed to reading the formula for the difference between cubes a - b 3 = a 3 - 3 a 2 b + 3 a b 2 - b 3. The cube of the difference of two expressions a and b is equal to the cube of the first expression minus three times the square of the first expression and the second, plus three times the square of the second expression and the first expression, minus the cube of the second expression.

The fifth formula a 2 - b 2 = a - b a + b (difference of squares) reads as follows: the difference of the squares of two expressions is equal to the product of the difference and the sum of the two expressions.

Expressions like a 2 + a b + b 2 and a 2 - a b + b 2 for convenience are called, respectively, the incomplete square of the sum and the incomplete square of the difference.

With this in mind, the formulas for the sum and difference of the cubes will read as follows:

The sum of the cubes of two expressions is equal to the product of the sum of these expressions by the incomplete square of their difference.

The difference between the cubes of two expressions is equal to the product of the difference between these expressions and the incomplete square of their sum.

Proof of FSO

It is quite easy to prove the FSO. Based on the properties of multiplication, we multiply the parts of the formulas in parentheses.

For example, consider the formula for the square of the difference.

a - b 2 = a 2 - 2 a b + b 2.

To raise an expression to the second power, you need to multiply this expression by itself.

a - b 2 = a - b a - b.

Let's expand the brackets:

a - b a - b = a 2 - a b - b a + b 2 = a 2 - 2 a b + b 2.

The formula is proven. The rest of the FSOs are proved in a similar way.

Examples of FSU application

The purpose of using abbreviated multiplication formulas is to multiply and exponentiate expressions quickly and concisely. However, this is not the entire scope of the FSO. They are widely used in abbreviating expressions, reducing fractions, factoring polynomials. Here are some examples.

Example 1. FSO

Simplify the expression 9 y - (1 + 3 y) 2.

We apply the formula for the sum of squares and get:

9 y - (1 + 3 y) 2 = 9 y - (1 + 6 y + 9 y 2) = 9 y - 1 - 6 y - 9 y 2 = 3 y - 1 - 9 y 2

Example 2. FSO

Reduce the fraction 8 x 3 - z 6 4 x 2 - z 4.

Note that the expression in the numerator is the difference between the cubes, and the denominator is the difference in the squares.

8 x 3 - z 6 4 x 2 - z 4 = 2 x - z (4 x 2 + 2 x z + z 4) 2 x - z 2 x + z.

We shorten and get:

8 x 3 - z 6 4 x 2 - z 4 = (4 x 2 + 2 x z + z 4) 2 x + z

FSOs also help to calculate the values ​​of expressions. The main thing is to be able to notice where to apply the formula. Let's show this with an example.

Let's square the number 79. Instead of cumbersome calculations, we write:

79 = 80 - 1 ; 79 2 = 80 - 1 2 = 6400 - 160 + 1 = 6241 .

It would seem that a complex calculation was carried out quickly with just using the abbreviated multiplication formulas and the multiplication table.

Another important point is the selection of the square of the binomial. The expression 4 x 2 + 4 x - 3 can be converted to 2 x 2 + 2 · 2 · x · 1 + 1 2 - 4 = 2 x + 1 2 - 4. Such transformations are widely used in integration.

If you notice an error in the text, please select it and press Ctrl + Enter

Abbreviated expression formulas are very often used in practice, so it is advisable to learn all of them by heart. Until this moment, it will serve us faithfully, which we recommend to print and keep in front of our eyes all the time:

The first four formulas from the compiled table of abbreviated multiplication formulas allow you to square and cube the sum or difference of two expressions. The fifth is for brief multiplication of the difference and the sum of two expressions. And the sixth and seventh formulas are used to multiply the sum of two expressions a and b by their incomplete square of the difference (this is the name of an expression of the form a 2 - a b + b 2) and the difference of two expressions a and b by the incomplete square of their sum (a 2 + a b + b 2) respectively.

It should be noted separately that each equality in the table is an identity. This explains why abbreviated multiplication formulas are also called abbreviated multiplication identities.

When solving examples, especially in which the factorization of a polynomial takes place, FSO is often used in the form with rearranged left and right sides:

The last three identities in the table have their own names. The formula a 2 - b 2 = (a - b) (a + b) is called by the difference of squares formula, a 3 + b 3 = (a + b) (a 2 −a b + b 2) - the formula for the sum of cubes, a a 3 −b 3 = (a − b) (a 2 + a b + b 2) - the formula for the difference of cubes... Please note that we did not name the FSU for the corresponding formulas with rearranged parts from the previous table.

Additional formulas

It doesn't hurt to add a few more identities to the table of abbreviated multiplication formulas.

Fields of application of abbreviated multiplication formulas (FSU) and examples

The main purpose of the abbreviated multiplication formulas (fsu) is explained by their name, that is, it consists in a brief multiplication of expressions. However, the scope of the FSU is much broader, and is not limited to short multiplication. Let's list the main directions.

Undoubtedly, the central application of the abbreviated multiplication formula was found in performing identical transformations of expressions. Most often, these formulas are used in the process simplifying expressions.

Example.

Simplify the expression 9 y− (1 + 3 y) 2.

Solution.

In this expression, squaring can be performed in abbreviated form, we have 9 y− (1 + 3 y) 2 = 9 y− (1 2 + 2 1 3 y + (3 y) 2)... It remains only to open the brackets and bring similar terms: 9 y− (1 2 + 2 1 3 y + (3 y) 2) = 9 y − 1−6 y − 9 y 2 = 3 y − 1−9 y 2.

In the numerator, the expression is the difference between the cubes of the two expressions 2 x and z 2, and in the denominator, the difference between the squares of these expressions. After applying the appropriate formulas, the original fraction will take the form ... Now you can cancel the same factors in the numerator and denominator:.

Let's summarize the entire solution briefly:

Answer:

.

Abbreviated multiplication formulas sometimes allow you to rationally evaluate the values ​​of expressions. As an example, let's show how you can square the number 79 using the squared difference formula: 79 2 = (80−1) 2 = 80 2 −2 80 1 + 1 2 = 6 400-160 + 1 = 6 241. This approach allows such calculations to be performed even orally.

In conclusion, let's say one more important transformation - selection of a square of a binomial, which is based on the formula for abbreviated multiplication by the square of the sum. For example, 4 x 2 + 4 x − 3 can be converted to (2 x) 2 + 2 2 x 1 + 1 2 −4, and the first three terms are replaced using the square of the sum formula. So the expression takes the form (2 x + 1) 2 −4. Such transformations are widely used, for example, for.

Bibliography.

• Algebra: study. for 7 cl. general education. institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; ed. S. A. Telyakovsky. - 17th ed. - M.: Education, 2008 .-- 240 p. : ill. - ISBN 978-5-09-019315-3.
• A. G. Mordkovich Algebra. 7th grade. At 2 pm Part 1. Textbook for students of educational institutions / A. G. Mordkovich. - 13th ed., Rev. - M .: Mnemozina, 2009 .-- 160 p.: Ill. ISBN 978-5-346-01198-9.
• Gusev V.A., Mordkovich A.G. Mathematics (manual for applicants to technical schools): Textbook. manual. - M .; Higher. shk., 1984.-351 p., ill.

Abbreviated multiplication formulas. Workout.

Try to calculate the following expressions in this way:

Answers:

Or, if you know the squares of the basic two-digit numbers, remember how many will be? Remembered? ... Fine! Since we are squaring, we must multiply by. It turns out that.

Remember that the formulas for the square of the sum and the square of the difference are not only valid for numeric expressions:

Calculate the following expressions yourself:

Answers:

Abbreviated multiplication formulas. Bottom line.

Let's summarize and write the formulas for the square of the sum and difference in one line:

Now let's practice "collecting" the formula from the expanded view to the view. We will need this skill later when converting large expressions.

Let's say we have the following expression:

We know that the square of the sum (or difference) is square of one number square of another number and twice the product of these numbers.

In this problem, it is easy to see the square of one number - this. Accordingly, one of the numbers in the parenthesis is the square root of, that is

Since there is in the second term, it means that this is the double product of one and the other number, respectively:

Where is the second number included in our parenthesis.

The second number in the parenthesis is.

Let's check. should be equal. Indeed, it is, which means that we found both numbers in parentheses: and. It remains to determine the sign that stands between them. What do you think the sign will be there?

Right! Since we add doubled product, then there will be an addition sign between the numbers. Now write down the transformed expression. Did you manage? You should have something like this:

Note: changing the places of the terms does not affect the result (it does not matter if the addition or subtraction is between and).

It is not at all necessary that the terms in the transformed expression stand as written in the formula. Look at this expression:. Try transforming it yourself. Happened?

Practice it - transform the following expressions:

Answers: Did you manage? Let's fix the topic. Choose from the expressions below those that can be represented as the square of the sum or the difference.

1. - prove that it is equivalent.

1. - cannot be represented as a square; one could imagine if instead there was.

Difference of squares

Another formula for abbreviated multiplication is the difference of squares.

The difference of squares is not the square of the difference!

The difference between the squares of two numbers is equal to the product of the sum of these numbers by their difference:

Let's check if this formula is correct. To do this, we multiply, as we did when deriving the formulas for the square of the sum and difference:

Thus, we have just verified that the formula is indeed correct. This formula also simplifies complex computational steps. Let's give an example:

You need to calculate:. Of course, we can square, then square and subtract one from the other, but the formula makes things easier for us:

Happened? Let's check the results:

Just like the square of the sum (difference), the formula for the difference of squares can be applied not only with numbers:

The ability to decompose the difference of squares will help us transform complex mathematical expressions.

Pay attention:

Since, when squaring the difference of the right expression, we get

Be careful and see which particular term is being squared! To reinforce the topic, transform the following expressions:

Did you write it down? Let's compare the obtained expressions:

Now that you have mastered the square of the sum and the square of the difference, as well as the difference of the squares, let's try to solve examples for a combination of these three formulas.

Transformation of elementary expressions (square of sum, square of difference, difference of squares)

Let's say we are given an example

It is necessary to simplify this expression. Look closely, what do you see in the numerator? That's right, the numerator is a perfect square:

When simplifying an expression, remember that the clue on which direction to move in simplification is in the denominator (or in the numerator). In our case, when the denominator is expanded and nothing else can be done, we can understand that the numerator will be either the square of the sum or the square of the difference. As we add, it becomes clear that the numerator is the square of the sum.

Try to transform the following expressions yourself:

Happened? We compare the answers and move on!

Sum cube and difference cube

The formulas cube of sum and cube of difference are displayed in the same way as the square of the sum and squared difference: by opening parentheses when multiplying terms by each other.

If the square of the sum and the square of the difference are very easy to remember, then the question arises "how to remember cubes?"

Take a close look at the two formulas described in comparison with the squaring of similar terms:

What pattern do you see?

1. When erected in square we have square first number and square second; when erected in a cube - there is cube one number and cube another number.

2. When erected in square, we have doubled product of numbers (numbers in 1 degree, which is one degree less than the one to which we raise the expression); when erected in cube - triple a product in which one of the numbers is squared (which is also 1 power less than the power to which we raise the expression).

3. When squaring, the sign in brackets in the expanded expression is reflected when adding (or subtracting) a doubled product - if addition is in brackets, then we add, if subtraction, we subtract; when building a cube, the rule is: if we have a sum cube, then all the signs are "+", and if the cube is a difference, then the signs alternate: "" - "" - "" - "".

All of the above, except for the dependence of the degrees when multiplying terms, is shown in the figure.

Let's practice? Expand the parentheses in the following expressions:

Compare the resulting expressions:

Difference and sum of cubes

Consider the last pair of formulas, difference and sum of cubes.

As we remember, in the difference of squares we have the multiplication of the difference and the sum of these numbers by one another. The difference of cubes and the sum of cubes also have two brackets:

1 parenthesis - the difference (or sum) of numbers in the first degree (depending on whether we reveal the difference or the sum of cubes);

2 bracket - an incomplete square (take a closer look: if we subtracted (or added) the double product of numbers, there would be a square), the sign when multiplying numbers is opposite to the sign of the original expression.

To fix the topic, let's solve a few examples:

Compare the resulting expressions:

Workout

Answers:

Let's summarize:

There are 7 formulas for abbreviated multiplication:

ADVANCED LEVEL

Abbreviated multiplication formulas are formulas, knowing which you can avoid performing some standard actions when simplifying expressions or factoring polynomials. You need to know the abbreviated multiplication formulas by heart!

1. Sum squared two expressions is equal to the square of the first expression plus twice the product of the first expression by the second plus the square of the second expression:
2. Difference squared two expressions is equal to the square of the first expression minus twice the product of the first expression by the second plus the square of the second expression:
3. Difference of squares two expressions is equal to the product of the difference of these expressions and their sum:
4. Sum cube of two expressions is equal to the cube of the first expression plus three times the square of the first expression and the second plus three times the product of the first expression and the square of the second plus the cube of the second expression:
5. Difference cube of two expressions is equal to the cube of the first expression minus the triple product of the square of the first expression by the second plus triple the product of the first expression by the square of the second minus the cube of the second expression:
6. Sum of cubes two expressions is equal to the product of the sum of the first and second expressions by the incomplete square of the difference of these expressions:
7. Difference of cubes two expressions is equal to the product of the difference of the first and second expressions by the incomplete square of the sum of these expressions:

Now let us prove all these formulas.

Abbreviated multiplication formulas. Proof.

1. .
To square an expression is to multiply it by itself:
.

Let's open the brackets and give similar ones:

2. .
We do the same: we multiply the difference by itself, open the parentheses and give similar ones:
.

3. .
Let's take the expression on the right side and expand the brackets:
.

4. .
A number in a cube can be represented as this number multiplied by its square:

Likewise:

In the difference of cubes, the signs alternate.

6. .

.

7. .
Let's expand the brackets on the right side:
.

Application of abbreviated multiplication formulas when solving examples

Example 1:

Find the meaning of the expressions:

Solution:

1. We use the formula for the square of the sum:.
2. We represent this number as a difference and use the formula for the square of the difference:.

Example 2:

Find the meaning of the expression:.

Solution:

Using the formula for the difference between the squares of the two expressions, we get:

Example 3:

Simplify the expression:

Solution in two ways:

Let's use the formulas the square of the sum and the square of the difference:

Method II.

Let's use the formula for the difference between the squares of the two expressions:

NOW YOUR WORD ...

I've told you everything I know about abbreviated multiplication formulas.

Tell me now, will you use them? If not, why not?

How do you like this article?

Perhaps you have questions. Or suggestions.

Write in the comments. We read all comments and respond to all.

And good luck with your exams!

In the previous lesson, we figured out factoring. We mastered two methods: taking the common factor out of parentheses and grouping. In this tutorial, the next powerful way is: abbreviated multiplication formulas... In short - FSU.

Abbreviated multiplication formulas (square of sum and difference, cube of sum and difference, difference of squares, sum and difference of cubes) are essential in all branches of mathematics. They are used in simplifying expressions, solving equations, multiplying polynomials, canceling fractions, solving integrals, etc. etc. In short, there is every reason to deal with them. Understand where they come from, why they are needed, how to remember them and how to apply them.

Understanding?)

Where do abbreviated multiplication formulas come from?

Equalities 6 and 7 are not written in a very familiar way. As if the opposite. This is on purpose.) Any equality works both left-to-right and right-to-left. In such a record, it is clearer where the FSO comes from.

They come from multiplication.) For example:

(a + b) 2 = (a + b) (a + b) = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2

That's all, no scientific tricks. We just multiply the parentheses and give the similar ones. So it turns out all abbreviated multiplication formulas. Abbreviated multiplication is because in the formulas themselves there is no multiplication of parentheses and a cast of similar ones. Abbreviated.) The result is immediately given.

FSO needs to be known by heart. Without the first three, you can not dream of a three, without the rest - of a four and an A.)

Why do we need abbreviated multiplication formulas?

There are two reasons to learn, even to memorize these formulas. The first is that a ready-made answer on the machine sharply reduces the number of errors. But this is not the main reason. But the second ...

If you like this site ...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Instant validation testing. Learning - with interest!)

you can get acquainted with functions and derivatives.