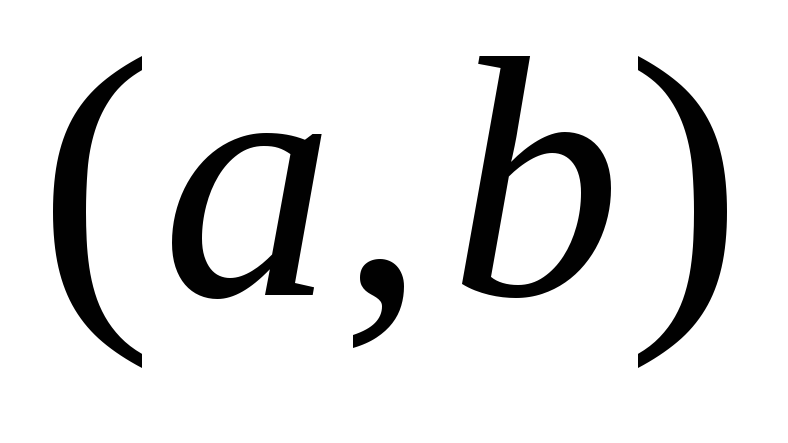Intervalle der Zunahme und Abnahme funktionieren online. Funktionsforschung

Extreme Funktionen

Definition 2

Der Punkt $ x_0 $ wird als Maximalpunkt der Funktion $ f (x) $ bezeichnet, wenn es eine Nachbarschaft dieses Punktes gibt, so dass für alle $ x $ aus dieser Nachbarschaft die Ungleichung $ f (x) \\ le f (x_0) $ gilt.

Definition 3

Der Punkt $ x_0 $ wird als Maximalpunkt der Funktion $ f (x) $ bezeichnet, wenn zu diesem Punkt eine Nachbarschaft existiert, so dass für alle $ x $ aus dieser Nachbarschaft die Ungleichung $ f (x) \\ ge f (x_0) $ gilt.

Das Konzept eines Extremums einer Funktion ist eng mit dem Konzept eines kritischen Punkts einer Funktion verbunden. Wir führen seine Definition ein.

Definition 4

$ x_0 $ heißt der kritische Punkt der Funktion $ f (x) $, wenn:

1) $ x_0 $ ist der interne Punkt der Definitionsdomäne;

2) $ f "\\ left (x_0 \\ right) \u003d 0 $ oder existiert nicht.

Für das Konzept eines Extremums kann man Theoreme auf ausreichende und notwendige Bedingungen für seine Existenz formulieren.

Satz 2

Eine ausreichende Bedingung für das Extrem

Der Punkt $ x_0 $ sei kritisch für die Funktion $ y \u003d f (x) $ und liege im Intervall $ (a, b) $. Angenommen, in jedem Intervall $ \\ left (a, x_0 \\ right) \\ und \\ (x_0, b) $ existiert die Ableitung $ f "(x) $ und behält ein konstantes Vorzeichen bei. Dann:

1) Wenn im Intervall $ (a, x_0) $ die Ableitung $ f "\\ left (x \\ right)\u003e 0 $ ist und im Intervall $ (x_0, b) $ die Ableitung $ f" \\ left (x \\ right) ist

2) Wenn im Intervall $ (a, x_0) $ die Ableitung $ f "\\ left (x \\ right) 0 $ ist, dann ist der Punkt $ x_0 $ der minimale Punkt für diese Funktion.

3) Wenn im Intervall $ (a, x_0) $ und im Intervall $ (x_0, b) $ die Ableitung $ f "\\ left (x \\ right)\u003e 0 $ oder die Ableitung $ f" \\ left (x \\ right)

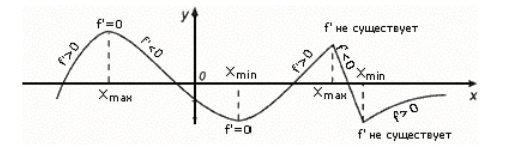
Dieser Satz ist in Abbildung 1 dargestellt.

Abbildung 1. Eine ausreichende Bedingung für die Existenz von Extrema

Beispiele für Extreme (Abb. 2).

Abbildung 2. Beispiele für Extrempunkte

  Regel der Funktionsforschung am Extremum

2) Finden Sie die Ableitung von $ f "(x) $;

7) Ziehe mit Theorem 2 Schlussfolgerungen über das Vorhandensein von Maxima und Minima in jedem Intervall.

  Funktion erhöhen und verringern

Wir führen zunächst die Definition von zunehmenden und abnehmenden Funktionen ein.

Definition 5

Die Funktion $ y \u003d f (x) $, die für das Intervall $ X $ definiert wurde, wird als Erhöhung bezeichnet, wenn für Punkte $ x_1 x_2 \\ in X $ für $ x_1 gilt

Definition 6

Die im Intervall $ X $ definierte Funktion $ y \u003d f (x) $ heißt absteigend, wenn für $ x_1, x_2 \\ in X $ für $ x_1f (x_2) $.

  Untersuchung der Funktion der Zunahme und Abnahme

Mit der Ableitung können Sie die Funktionen zum Erhöhen und Verringern erkunden.

Um die Funktion für Anstiegs- und Abfallintervalle zu untersuchen, ist Folgendes erforderlich:

1) Finden Sie die Domäne der Funktion $ f (x) $;

2) Finden Sie die Ableitung von $ f "(x) $;

3) Finde die Punkte, an denen die Gleichheit $ f "\\ left (x \\ right) \u003d 0 $ gilt;

4) Finde die Punkte, an denen $ f "(x) $ nicht existiert;

5) Markieren Sie auf der Koordinatenlinie alle gefundenen Punkte und den Bereich dieser Funktion.

6) Bestimmen Sie das Vorzeichen der Ableitung $ f "(x) $ für jedes resultierende Intervall;

7) Zum Schluss: In Intervallen, in denen $ f "\\ left (x \\ right) 0 $ ist, erhöht sich die Funktion.

  Beispiele für Aufgaben zur Untersuchung von Funktionen zum Erhöhen, Verringern und zum Vorhandensein von Extrempunkten

Beispiel 1

Untersuchen Sie die Funktion des Erhöhens und Verringerns sowie das Vorhandensein von Maximal- und Minimalpunkten: $ f (x) \u003d (2x) ^ 3-15x ^ 2 + 36x + 1 $

Da die ersten 6 Punkte gleich sind, fangen wir damit an.

1) Geltungsbereich - alle reellen Zahlen;

2) $ f "\\ left (x \\ right) \u003d 6x ^ 2-30x + 36 $;

3) $ f "\\ left (x \\ right) \u003d 0 $;

\ \ \

4) $ f "(x) $ existiert an allen Stellen im Definitionsbereich;

5) Koordinatenzeile:

Abbildung 3

6) Bestimmen Sie das Vorzeichen der Ableitung $ f "(x) $ für jedes Intervall:

  \\ \\ wenn für ein Punktepaar x  und x ", und ≤ x die Ungleichung f(x) ≤ f (x ") und streng steigend - wenn die Ungleichung f (x) f(x ") Das Verringern und das strikte Verringern einer Funktion werden auf ähnliche Weise definiert. Zum Beispiel die Funktion bei = x 2 (fig. , a) im Segment stark zunimmt und

(fig. , b) nimmt in diesem Segment strikt ab. Zunehmende Funktionen sind mit gekennzeichnet f (x) und abnehmend f (x) ↓. Um differenzierbar zu funktionieren f (x) nahm im Segment zu [ aber, b] ist es notwendig und ausreichend, dass seine Ableitung f"(x) war am [nicht negativ aber, b].

Zusammen mit der Zunahme und Abnahme der Funktion auf dem Segment wird die Zunahme und Abnahme der Funktion an dem Punkt berücksichtigt. Funktion bei = f (x) wird an dieser Stelle als ansteigend bezeichnet x  0, wenn es ein solches Intervall (α, β) gibt, das den Punkt enthält x  0 das für jeden Punkt x  aus (α, β), x\u003e x  0, die Ungleichung f (x 0) ≤ f (x) und für jeden Punkt x  aus (α, β), x 0, die Ungleichung f (x) ≤ f (x  0). Ebenso eine strikte Erhöhung der Funktion an der Stelle x  0. Wenn f"(x 0) >   0, dann die Funktion f(x) nimmt an dieser Stelle strikt zu x  0. Wenn f (x) erhöht sich an jedem Punkt des Intervalls ( a, b), dann erhöht es sich in diesem Intervall.

  S. B. Stechkin.

Große sowjetische Enzyklopädie. - M .: Sowjetische Enzyklopädie. 1969-1978 .

Sehen Sie, was "Erhöhen und Verringern der Funktion" in anderen Wörterbüchern bedeutet:

Die Konzepte der mathematischen Analyse. Die Funktion f (x) heißt das Verhältnis der Anzahl der unterschiedlichen Altersgruppen der Bevölkerung, die im Segment ALTERSBESTANDSSTRUKTUR zunimmt. Abhängig von Fruchtbarkeit und Mortalität, Lebenserwartung der Menschen ... Großes Lexikon

Die Konzepte der mathematischen Analyse. Die Funktion f (x) heißt auf dem Segment ansteigend, wenn für ein Punktepaar x1 und x2 a≤x1 ... Enzyklopädisches Wörterbuch

Die Konzepte der Mathematik. Analyse. Die Funktion f (x) wird aufgerufen Erhöhen auf dem Segment [a, b], wenn für ein Paar von Punkten x1 und x2 und<или=х1 <х<или=b, выполняется неравенство f(x1)Naturgeschichte. Enzyklopädisches Wörterbuch

Ein Zweig der Mathematik, der Ableitungen und Differentiale von Funktionen und deren Anwendung auf das Studium von Funktionen untersucht. Design D. und. in eine unabhängige mathematische Disziplin mit den Namen von I. Newton und G. Leibniz (zweite Hälfte ... Große sowjetische Enzyklopädie

Die mathematische Sektion, in der die Konzepte der Ableitung und des Differentials untersucht werden, und Methoden ihrer Anwendung auf die Untersuchung von Funktionen. D.'s Entwicklung und. eng verwandt mit der Entwicklung der Integralrechnung. Untrennbar mit ihrem Inhalt. Zusammen bilden sie die Basis ... ... Mathematische Enzyklopädie

Dieser Begriff hat andere Bedeutungen, siehe Funktion. Die Anfrage "Anzeige" wird hier umgeleitet; Siehe auch andere Bedeutungen ... Wikipedia

Aristoteles und Peripatetik  - Die Aristoteles-Frage Das Leben des Aristoteles Aristoteles wurde 384/383 geboren. BC e. in Stagira, an der Grenze zu Mazedonien. Sein Vater, Nikomachos, war Arzt im Dienste des mazedonischen Königs Amyntos, des Vaters Philipps. Zusammen mit der Familie hat der junge Aristoteles ... ... Die westliche Philosophie von ihren Anfängen bis heute

  - (QCD), eine Quantenfeldtheorie der starken Wirkung von Quarks und Gluonen, konstruiert im Bild eines Quanten. Elektrodynamik (QED) basierend auf der Farbsymmetrie. Im Gegensatz zu QED haben die Fermionen in QCD eine Ergänzung. Freiheitsgrad Quanten. Nummer, ... ... Physische Enzyklopädie

I Herz Das Herz (lat. Cor, griechische Kardia) ist ein hohles fibromuskuläres Organ, das als Pumpe für die Blutbewegung im Kreislauf sorgt. Anatomie Das Herz befindet sich im vorderen Mediastinum (Mediastinum) im Perikard zwischen ... ... Medizinische Enzyklopädie

Das Leben einer Pflanze ist wie jedes andere Lebewesen ein komplexer Satz miteinander verbundener Prozesse. Das wichtigste davon ist der Stoffwechsel mit der Umwelt. Die Umwelt ist die Quelle, aus der ... ... Biologische Enzyklopädie

Extreme Funktionen

Definition 2

Der Punkt $ x_0 $ wird als Maximalpunkt der Funktion $ f (x) $ bezeichnet, wenn es eine Nachbarschaft dieses Punktes gibt, so dass für alle $ x $ aus dieser Nachbarschaft die Ungleichung $ f (x) \\ le f (x_0) $ gilt.

Definition 3

Der Punkt $ x_0 $ wird als Maximalpunkt der Funktion $ f (x) $ bezeichnet, wenn zu diesem Punkt eine Nachbarschaft existiert, so dass für alle $ x $ aus dieser Nachbarschaft die Ungleichung $ f (x) \\ ge f (x_0) $ gilt.

Das Konzept eines Extremums einer Funktion ist eng mit dem Konzept eines kritischen Punkts einer Funktion verbunden. Wir führen seine Definition ein.

Definition 4

$ x_0 $ heißt der kritische Punkt der Funktion $ f (x) $, wenn:

1) $ x_0 $ ist der interne Punkt der Definitionsdomäne;

2) $ f "\\ left (x_0 \\ right) \u003d 0 $ oder existiert nicht.

Für das Konzept eines Extremums kann man Theoreme auf ausreichende und notwendige Bedingungen für seine Existenz formulieren.

Satz 2

Eine ausreichende Bedingung für das Extrem

Der Punkt $ x_0 $ sei kritisch für die Funktion $ y \u003d f (x) $ und liege im Intervall $ (a, b) $. Angenommen, in jedem Intervall $ \\ left (a, x_0 \\ right) \\ und \\ (x_0, b) $ existiert die Ableitung $ f "(x) $ und behält ein konstantes Vorzeichen bei. Dann:

1) Wenn im Intervall $ (a, x_0) $ die Ableitung $ f "\\ left (x \\ right)\u003e 0 $ ist und im Intervall $ (x_0, b) $ die Ableitung $ f" \\ left (x \\ right) ist

2) Wenn im Intervall $ (a, x_0) $ die Ableitung $ f "\\ left (x \\ right) 0 $ ist, dann ist der Punkt $ x_0 $ der minimale Punkt für diese Funktion.

3) Wenn im Intervall $ (a, x_0) $ und im Intervall $ (x_0, b) $ die Ableitung $ f "\\ left (x \\ right)\u003e 0 $ oder die Ableitung $ f" \\ left (x \\ right)

Dieser Satz ist in Abbildung 1 dargestellt.

Abbildung 1. Eine ausreichende Bedingung für die Existenz von Extrema

Beispiele für Extreme (Abb. 2).

Abbildung 2. Beispiele für Extrempunkte

  Regel der Funktionsforschung am Extremum

2) Finden Sie die Ableitung von $ f "(x) $;

7) Ziehe mit Theorem 2 Schlussfolgerungen über das Vorhandensein von Maxima und Minima in jedem Intervall.

  Funktion erhöhen und verringern

Wir führen zunächst die Definition von zunehmenden und abnehmenden Funktionen ein.

Definition 5

Die Funktion $ y \u003d f (x) $, die für das Intervall $ X $ definiert wurde, wird als Erhöhung bezeichnet, wenn für Punkte $ x_1 x_2 \\ in X $ für $ x_1 gilt

Definition 6

Die im Intervall $ X $ definierte Funktion $ y \u003d f (x) $ heißt absteigend, wenn für $ x_1, x_2 \\ in X $ für $ x_1f (x_2) $.

  Untersuchung der Funktion der Zunahme und Abnahme

Mit der Ableitung können Sie die Funktionen zum Erhöhen und Verringern erkunden.

Um die Funktion für Anstiegs- und Abfallintervalle zu untersuchen, ist Folgendes erforderlich:

1) Finden Sie die Domäne der Funktion $ f (x) $;

2) Finden Sie die Ableitung von $ f "(x) $;

3) Finde die Punkte, an denen die Gleichheit $ f "\\ left (x \\ right) \u003d 0 $ gilt;

4) Finde die Punkte, an denen $ f "(x) $ nicht existiert;

5) Markieren Sie auf der Koordinatenlinie alle gefundenen Punkte und den Bereich dieser Funktion.

6) Bestimmen Sie das Vorzeichen der Ableitung $ f "(x) $ für jedes resultierende Intervall;

7) Zum Schluss: In Intervallen, in denen $ f "\\ left (x \\ right) 0 $ ist, erhöht sich die Funktion.

  Beispiele für Aufgaben zur Untersuchung von Funktionen zum Erhöhen, Verringern und zum Vorhandensein von Extrempunkten

Beispiel 1

Untersuchen Sie die Funktion des Erhöhens und Verringerns sowie das Vorhandensein von Maximal- und Minimalpunkten: $ f (x) \u003d (2x) ^ 3-15x ^ 2 + 36x + 1 $

Da die ersten 6 Punkte gleich sind, fangen wir damit an.

1) Geltungsbereich - alle reellen Zahlen;

2) $ f "\\ left (x \\ right) \u003d 6x ^ 2-30x + 36 $;

3) $ f "\\ left (x \\ right) \u003d 0 $;

\ \ \

4) $ f "(x) $ existiert an allen Stellen im Definitionsbereich;

5) Koordinatenzeile:

Abbildung 3

6) Bestimmen Sie das Vorzeichen der Ableitung $ f "(x) $ für jedes Intervall:

\ \.

Der Bereich der Funktionswerte ist Intervall [1; 3].

1. Für x \u003d -3, x \u003d -1, x \u003d 1,5, x \u003d 4,5 ist der Wert der Funktion Null.

Der Wert des Arguments, bei dem der Wert der Funktion Null ist, wird Null der Funktion genannt.

// d.h. für diese Funktion die Zahlen -3; -1; 1,5; 4,5 sind Nullen.

2. In Abständen [4,5; 3) und (1; 1,5) und (4,5; 5,5] befindet sich der Graph der Funktion f oberhalb der Abszissenachse und in Intervallen (-3; -1) und (1,5; 4,5) unterhalb der Achse Abszisse kann dies wie folgt erklärt werden: in Intervallen [4,5; 3) und (1; 1,5) und (4,5; 5,5] nimmt die Funktion positive Werte an und in Intervallen (-3; -1) und ( 1,5; 4,5) negativ.

Jedes der angegebenen Intervalle (in denen die Funktion Werte desselben Vorzeichens annimmt) wird als Intervall mit konstantem Vorzeichen der Funktion f.//t.e bezeichnet. Nehmen wir zum Beispiel das Intervall (0; 3), dann ist es kein Intervall des konstanten Vorzeichens dieser Funktion.

In der Mathematik ist es bei der Suche nach Intervallen mit konstantem Vorzeichen einer Funktion üblich, Intervalle mit maximaler Länge anzugeben. // d.h. der Spalt (2; 3) ist konstantes Vorzeichen  Funktion f, aber die Antwort sollte das Intervall enthalten [4,5; 3) den Spalt (2; 3) enthält.

3. Wenn Sie sich entlang der Abszisse von 4,5 auf 2 bewegen, werden Sie feststellen, dass der Graph der Funktion abnimmt, dh die Werte der Funktion sinken. // In der Mathematik ist es üblich zu sagen, dass im Intervall [4,5; 2] die Funktion nimmt ab.

Wenn x von 2 auf 0 ansteigt, steigt der Funktionsgraph an, d.h. Funktionswerte erhöhen sich. // In der Mathematik ist es üblich zu sagen, dass im Intervall [2; 0] Funktion erhöht sich.

Eine Funktion f wird aufgerufen, wenn für zwei beliebige Werte des Arguments x1 und x2 aus diesem Intervall x2\u003e x1 die Ungleichung f (x2)\u003e f (x1) gilt. // oder Funktion aufgerufen in einem gewissen Intervall zunehmenwenn für irgendwelche Argumentwerte aus diesem Intervall ein größerer Wert der Funktion einem größeren Wert des Arguments entspricht, // d.h. je mehr x, desto mehr y.

Die Funktion f wird aufgerufen in gewissen Abständen abnehmendwenn für zwei beliebige Werte des Arguments x1 und x2 aus diesem Intervall x2\u003e x1 die Ungleichung f (x2) in einem bestimmten Intervall abnimmt, wenn für Werte des Arguments aus diesem Intervall ein größerer Wert des Arguments einem kleineren Wert der Funktion entspricht. // d.h. je mehr x, desto weniger y.

Steigt die Funktion über den gesamten Definitionsbereich an, so wird sie aufgerufen zunehmen.

Wenn die Funktion über die gesamte Domäne abnimmt, wird sie aufgerufen abnehmend.

Beispiel 1  die graphische Darstellung der ansteigenden bzw. abfallenden Funktionen.

Beispiel 2

Definieren Steigt oder sinkt die lineare Funktion f (x) \u003d 3x + 5?

Beweis. Wir verwenden die Definitionen. Sei x1 und x2 beliebige Werte des Arguments, mit x1< x2., например х1=1, х2=7

Basierend auf ausreichenden Vorzeichen gibt es Intervalle von zunehmenden und abnehmenden Funktionen.

Hier ist der Wortlaut der Zeichen:

• wenn die Ableitung der Funktion y \u003d f (x)  positiv für jeden x  vom Intervall X, dann erhöht sich die Funktion um X;
• wenn die Ableitung der Funktion y \u003d f (x)  negativ für jeden x  vom Intervall X, dann nimmt die Funktion ab X.

Um die Intervalle der Zunahme und Abnahme der Funktion zu bestimmen, ist es daher notwendig:

• finden Sie den Umfang der Funktion;

• finde die Ableitung der Funktion;

• zu den erhaltenen Intervallen fügen Sie Grenzpunkte hinzu, an denen die Funktion definiert und stetig ist.

Betrachten Sie ein Beispiel zur Erläuterung des Algorithmus.

Ein Beispiel.

Bestimmen Sie die Intervalle für die Erhöhung und Verringerung der Funktionen.

Lösung.

Der erste Schritt besteht darin, eine Wachstumsdefinition der Funktion zu finden. In unserem Beispiel sollte der Ausdruck im Nenner daher nicht verschwinden. .

Wir gehen zur Ableitungsfunktion über:

Um die Intervalle zunehmender und abnehmender Funktionen nach einem ausreichenden Kriterium zu bestimmen, lösen wir die Ungleichungen   und   auf dem Gebiet der Definition. Wir verwenden eine Verallgemeinerung der Intervallmethode. Die einzig gültige Zählerwurzel ist x \u003d 2und der Nenner verschwindet bei x \u003d 0. Diese Punkte unterteilen den Bereich in Intervalle, in denen die Ableitung der Funktion ihr Vorzeichen behält. Wir markieren diese Punkte auf der Zahlenlinie. Die Plus- und Minuszeichen bezeichnen willkürlich die Intervalle, in denen die Ableitung positiv oder negativ ist. Die Pfeile unten zeigen schematisch die Zunahme oder Abnahme der Funktion im entsprechenden Intervall.

Auf diese Weise,   und .

Auf den Punkt x \u003d 2  Die Funktion ist definiert und stetig, daher sollte sie sowohl zur Zunahme als auch zur Abnahme addiert werden. Auf den Punkt x \u003d 0  Die Funktion ist nicht definiert, daher ist dieser Punkt nicht in den erforderlichen Intervallen enthalten.

Wir geben eine graphische Darstellung der Funktion zum Vergleich der damit erzielten Ergebnisse.

Die Antwort lautet:  Funktion steigt mit   nimmt mit dem Intervall ab (0; 2] .

- Extrempunkte einer Funktion einer Variablen. Ausreichende Extrembedingungen

Angenommen, eine in einem Intervall definierte und stetige Funktion f (x) ist darin nicht monoton. Es wird solche Teile [,] des Intervalls geben, in denen der größte und der kleinste Wert durch die Funktion am internen Punkt erreicht werden, d. H zwischen und.

Es wird gesagt, dass eine Funktion f (x) an einem Punkt ein Maximum (oder Minimum) hat, wenn dieser Punkt von einer solchen Nachbarschaft (x 0 -, x 0 +) umgeben sein kann, die in dem Intervall enthalten ist, in dem die Funktion gegeben ist, dass die Ungleichung für alle ihre Punkte gilt.

f (x)< f(x 0)(или f(x)>f (x 0))

Mit anderen Worten, der Punkt x 0 liefert das Maximum (Minimum) für die Funktion f (x), wenn sich herausstellt, dass der Wert f (x 0) der größte (kleinste) der von der Funktion akzeptierten Werte in einer (zumindest kleinen) Nachbarschaft dieses Punktes ist. Es ist zu beachten, dass die Definition des Maximums (Minimums) voraussetzt, dass die Funktion auf beiden Seiten des Punkts x 0 gegeben ist.

Wenn es eine Nachbarschaft gibt, in der (für x \u003d x 0) die strenge Ungleichung gilt

f (x) f (x 0)

sie sagen, dass die Funktion am Punkt x 0 ein eigenes Maximum (Minimum) hat, andernfalls ist sie nicht korrekt.

Wenn die Funktion an den Punkten x 0 und x 1 Maxima hat, dann sehen wir bei Anwendung des zweiten Weierstraß-Theorems auf das Intervall, dass die Funktion in diesem Intervall an einem Punkt x 2 zwischen x 0 und x 1 ihren niedrigsten Wert erreicht und dort ein Minimum hat. In ähnlicher Weise wird es zwischen zwei Minima sicherlich ein Maximum geben. In diesem einfachsten (und in der Praxis wichtigsten) Fall, in dem eine Funktion im Allgemeinen nur eine endliche Anzahl von Maxima und Minima aufweist, wechseln sie sich einfach ab.

Beachten Sie, dass es zur Bezeichnung des Maximums oder Minimums einen Begriff gibt, der sie verbindet - das Extremum.

Die Begriffe Maximum (max f (x)) und Minimum (min f (x)) sind lokale Eigenschaften der Funktion und finden an einem bestimmten Punkt x 0 statt. Die Konzepte der größten (sup f (x)) und kleinsten (inf f (x)) Werte beziehen sich auf ein endliches Intervall und sind globale Eigenschaften einer Funktion auf dem Intervall.

Abbildung 1 zeigt, dass an den Punkten x 1 und x 3 lokale Maxima und an den Punkten x 2 und x 4 lokale Minima vorhanden sind. Die Funktion erreicht jedoch den kleinsten Wert bei x \u003d a und den größten bei x \u003d b.

Wir haben das Problem, alle Werte eines Arguments zu finden, die extreme Funktionen liefern. Bei der Lösung spielt das Derivat seine Hauptrolle.

Nehmen wir zunächst an, dass für die Funktion f (x) im Intervall (a, b) eine endliche Ableitung existiert. Wenn an einem Punkt x 0 die Funktion ein Extremum hat, schließen wir, indem wir auf das oben diskutierte Intervall (x 0 -, x 0 +) den Satz von Fermat anwenden, dass f (x) \u003d 0 dies eine notwendige Bedingung für das Extremum ist. Extreme sollten nur an den Stellen gesucht werden, an denen die Ableitung gleich Null ist.

Es sollte jedoch nicht gedacht werden, dass jeder Punkt, an dem die Ableitung gleich Null ist, Extremfunktionen liefert: Die gerade angegebene Bedingung ist nicht ausreichend