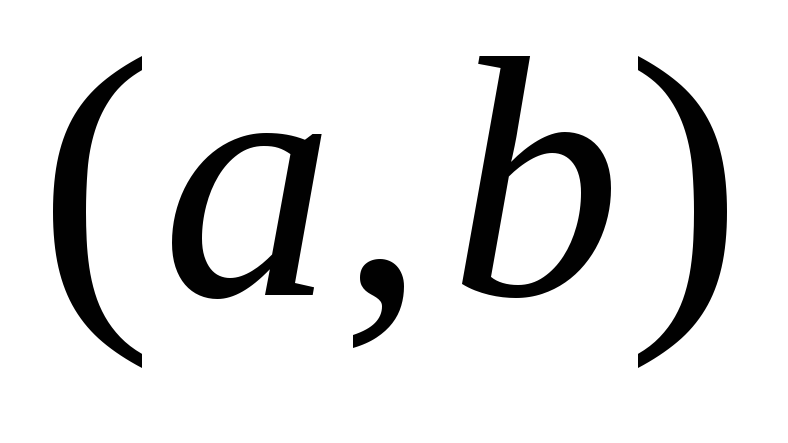Функцийн цоорхойг олох. "нэмэгдүүлэх, багасгах функц"

Функц гэж нэрлэдэг интервалд нэмэгдэх
ямар нэгэн зүйл байвал

тэгш бус байдлыг хадгалдаг
(аргументын илүү том утга нь функцийн том утгатай тохирч байна).

Үүний нэгэн адил функц
гэж дууддаг интервал дахь буурах
ямар нэгэн зүйл байвал
нөхцлийн дагуу энэ интервалаас
тэгш бус байдлыг хадгалдаг
(аргументын илүү том утга нь функцийн бага утгатай тохирч байна).

Интервал дээр нэмэгдэж байна
ба интервал дахь бууралт
функцууд гэж нэрлэдэг интервал дахь монотоник
.

Ялгаатай функцийн үүслийг мэдэх нь түүний монотон байдлын интервалыг олох боломжийг олгодог.

Теорем (функцийг нэмэгдүүлэх хангалттай нөхцөл).
чиг үүрэг
интервал дээр эерэг
дараа нь функц
энэ интервалд монотон байдлаар нэмэгддэг.

Теорем (функц буурах хангалттай нөхцөл). Хэрэв үүсмэл нь интервал дээр ялгаатай байвал
чиг үүрэг
интервал дээр сөрөг
дараа нь функц
энэ интервалд нэгэн зэрэг буурдаг.

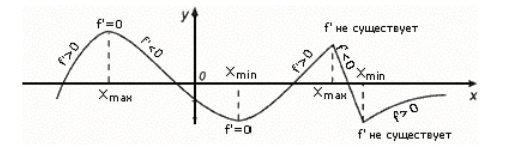
Геометрийн утга Эдгээр теоремуудын нэг нь функц буурах интервал дээр тэнхлэгийн дагуу функцын графикийн тангенс бүрдэнэ
өтгөн өнцөг, өсгөх завсарлагатай үед - хурц (1-р зургийг үз).

Теорем (функцийн монотон байдлын зайлшгүй нөхцөл).Хэрэв функц
ялгагдах ба
(
) интервал дээр
, дараа нь энэ интервалд буурахгүй (нэмэгдэхгүй).

Функцийн монотон байдлын интервалыг олох алгоритм
:

Нэг жишээ. Функцийн монотон байдлын интервалыг ол
.

Цэг гэж дууддаг функц хамгийн их цэг

тэр бүгдэд зориулсан нөхцлийг хангах
, тэгш бус байдал
.

Хамгийн их функц Хамгийн их цэг дэх функцийн утга юм.

Зураг 2-т цэгүүд дээрх максимумтай функцийн графикийн жишээг үзүүлэв
.

Цэг гэж дууддаг функц хамгийн бага цэг
хэрэв хэдэн тоо байдаг бол
тэр бүгдэд зориулсан нөхцлийг хангах
, тэгш бус байдал
Байна. Нарис. 2 функц нь нэг цэг дээр хамгийн бага байх ёстой .

Өндөр ба намуудын хувьд нийтлэг нэр байдаг - туйлын цэгүүд Байна. Үүний дагуу хамгийн их ба хамгийн бага цэгүүдийг дууддаг экстремум цэгүүд .

Энэ сегментэд тодорхойлогдсон функц нь хамгийн дээд хэмжээ нь зөвхөн энэ хэсгийн хүрээнд байх ёстой. Функцийн хамгийн дээд ба хамгийн бага утгыг сегмент дэх хамгийн том, хамгийн бага утгатай андуурч болохгүй. Эдгээр нь огт өөр ойлголт юм.

Экстремумын цэгүүдэд дериватив нь тусгай шинж чанартай байдаг.

Теорем (экстремумын зайлшгүй нөхцөл). Нэг цэг дээр үзье функц
экстремумтай. Дараа нь аль аль нь
огт байдаггүй
.

Тухайн функцийн домэйны цэгүүд
аль эсвэл байхгүй байна
гэж нэрлэдэг чухал цэгүүдийн функц .

Тиймээс экстремум цэгүүд эгзэгтэй цэгүүдийн дунд оршдог. Ерөнхийдөө, эгзэгтэй цэг нь экстремум цэг байх албагүй. Хэрэв ямар нэгэн цэгт функцийн дериватив нь тэгтэй тэнцүү бол энэ үед функц нь экстремумтай байна гэсэн үг биш юм.

Нэг жишээ. Авч үзье
Байна. Бидэнд байгаа
харин цэг
нь экстремум биш (3-р зургийг үз).

Теорем (экстремумын эхний хангалттай нөхцөл). Нэг цэг дээр үзье функц
тасралтгүй ба үүсмэл
цэгийг гатлах үед өөрчлөлт тэмдэг. Дараа нь - экстремумын цэг: хамгийн их, хэрэв тэмдэг нь "+" -ээс "-" хүртэл өөрчлөгдсөн бол хамгийн бага, хэрэв "-" -ээс "+" хүртэл байвал.

Хэрэв цэгийг гатлах үед үүсмэл нь дараа нь тэмдгийг өөрчлөхгүй экстремум байхгүй.

Теорем (экстремумын хоёрдахь хангалттай нөхцөл). Нэг цэг дээр үзье хоёр дахин ялгаатай функцийн үүсмэл
тэгтэй тэнцүү (
) бөгөөд энэ үед түүний хоёр дахь уламжлал нь тэг биш юм (
) цэгийн зарим хэсэгт тасралтгүй үргэлжилдэг Байна. Дараа нь - экстремумын цэг
; үед
энэ бол хамгийн бага цэг, хэзээ
энэ бол хамгийн дээд цэг.

Экстремумын анхны хангалттай нөхцлийг ашиглан функцын экстремаг олох алгоритм:

Деривативыг олоорой.

Функцийн чухал цэгүүдийг олох.

Деривативын тэмдгийг эгзэгтэй цэг бүрийн зүүн ба баруун талд шалгаж, экстрема байдаг гэж дүгнэ.

Функцийн хэт их утгыг ол.

Экстремумын хоёрдахь хангалттай нөхцлийг ашиглан функцын экстремаг олох алгоритм:

Нэг жишээ. Функцийн экстрема олох
.

1. Функцийн цар хүрээг ол

2. Функцийн үүсмэл зүйлийг ол

3. Деривийг тэг болгож, функцийн эгзэгтэй цэгүүдийг ол

4. Тодорхойлолтын талбарт чухал цэгүүдийг тэмдэглэ

5. Хүлээн авсан интервал бүр дээр деривативын тэмдгийг тооцоол

6. Завсарлага бүрт функцийн төлөв байдлыг олж мэд.

Жишээ: Өсөн нэмэгдэж буй болон буурах функцүүдийн интервалыг оле(х) = мөн интервал дахь энэ функцын тэгийн тоо.

Шийдэл:

1. D ( е) \u003d R

2. е"(х) =

D ( е") \u003d D ( е) \u003d R

3. Тэгшитгэлийг шийдвэрлэх замаар функцийн эгзэгтэй цэгүүдийг ол е"(х) = 0.

х(х – 10) = 0

үйл ажиллагааны чухал цэгүүд х \u003d 0 ба х = 10.

4. деривативын тэмдгийг тодорхойлно уу.

е"(х) + – +

е(х) 0 10 х

(-∞; 0) ба (10; + ∞) интервалуудад функцийн үүсмэл цэг нь цэг дээр эерэг байна х \u003d 0 ба x \u003d 10 функц е(х) нь тасралтгүй үргэлжлэх тул интервалаар энэ функц нэмэгддэг: (-∞; 0];.

Бид сегментийн төгсгөлд функцийн утгуудын тэмдгийг тодорхойлдог.

е(0) = 3, е(0) > 0

е(10) = , е(10) < 0.

Функц нь интервал дээр буурч, функцийн утгын тэмдэг өөрчлөгддөг тул энэ интервал дээр функцийн тэг тэг болно.

Хариулт: f (x) функц нь интервалаар нэмэгддэг: (-∞; 0] ;;

интервалд нэг функц тэг байна.

2. Функцийн экстремум цэгүүд: хамгийн их ба хамгийн бага цэгүүд. Функцийн экстремум байх шаардлагатай бөгөөд хангалттай нөхцөл. Экстремумын талаархи функциональ судалгааны дүрэм .

Тодорхойлолт 1:Үүсмэл нь тэгтэй тэнцэх цэгүүдийг эгзэгтэй буюу тогтмол гэж нэрлэдэг.

Тодорхойлолт 2. Хэрэв тухайн цэг дэх функцийн утга нь хамгийн ойрын функцээс бага (их) байвал тухайн функцийг хамгийн бага (хамгийн их) цэг гэж нэрлэдэг.

Энэ тохиолдолд хамгийн их ба хамгийн бага нь орон нутгийнх гэдгийг санах нь зүйтэй.

Инжирд. 1. орон нутгийн максима ба минимаг харуулав.

Хамгийн их ба хамгийн бага функцийг нийтлэг нэрээр нэгтгэдэг: Функцийн экстремум.

Теорем 1 (функцын экстремум байгаа эсэхийг баталгаажуулах шаардлагатай шинж тэмдэг). Хэрэв нэг цэг дээр ялгагдах функц энэ үед хамгийн их эсвэл хамгийн бага байх юм бол түүний дериватив нь алга болно.

Теорем 2 (функцын экстремум байгаа эсэх хангалттай шинж тэмдэг). Хэрэв тасралтгүй үйл ажиллагаа нь чухал цэгийг агуулсан тодорхой интервалын бүх цэг дээр үүсмэл байвал (мөн энэ цэгээс бусад тохиолдолд), хэрэв үүсмэл зүйл нь аргументыг эгнээний цэгээс зүүнээс баруун тийш дамжуулах үед тэмдгээс хасах тэмдгийг өөрчилдөг бол функц энэ үед хамгийн их байх ба тэмдгийг хасахаас нэмэх рүү шилжүүлбэл хамгийн бага байх ёстой.

Функцийн төлөв байдлын талаархи маш чухал мэдээллийг өсөлт, бууралтын интервалаар өгдөг. Тэдгээрийг олох нь функцийг судалж, зураг зурах үйл явцын нэг хэсэг юм. Нэмж дурдахад, өсөлтөөс буурах эсвэл буурахаас өсөх хүртэл өөрчлөлт ордог эрс тэс цэгүүдэд тодорхой интервал дахь функцийн хамгийн том, хамгийн бага утгыг олоход онцгой анхаарал хандуулдаг.

Энэ нийтлэлд бид шаардлагатай тодорхойлолтуудыг өгч, интервал дээрх функцийн өсөлт, бууралтын хангалттай шинж тэмдгийг томъёолж, экстремум оршин тогтнох нөхцлийг бүрдүүлж, энэ бүхэл бүтэн онолыг жишээ, асуудлыг шийдвэрлэхэд ашиглана

Хуудасны чиглүүлэлт.

Функцийн интервал дахь өсөлт, бууралт.

Өсөн нэмэгдэж буй функцын тодорхойлолт.

Y \u003d f (x) функц нь X интервал дээр нэмэгдэж, хэрэв байгаа бол тэгш бус байдлыг хадгалдаг. Өөрөөр хэлбэл аргументын илүү том утга нь функцийн том утгатай тохирч байна.

Буурах функцийн тодорхойлолт.

Y \u003d f (x) функц нь X интервал дээр буурна, хэрэв байгаа бол мөн тэгш бус байдлыг хадгалдаг Байна. Өөрөөр хэлбэл аргументын илүү том утга нь функцийн доод утгатай тохирч байна.

ТАЙЛБАР: Хэрэв функц нэмэгдэж, буурах интервалын төгсгөлд (a; b), өөрөөр хэлбэл x \u003d a ба x \u003d b бол тодорхойлогдож, тасралтгүй үргэлжилж байвал эдгээр цэгүүдийг өсгөх, буурах интервалд оруулна. Энэ нь X интервал дээр нэмэгдэж, буурах функцийн тодорхойлолтуудтай зөрчилддөггүй.

Жишээлбэл, үндсэн элемент функцүүдийн шинж чанараас харахад y \u003d sinx нь аргументын бүх бодит утгуудын хувьд тодорхойлогддог ба тасралтгүй байдаг. Тиймээс, интервал дахь синусын үйл ажиллагаа нэмэгдсэнээс эхлэн интервал нэмэгдэх талаар хэлж болно.

Функцийн экстремум, экстремумын цэгүүд.

Цэг гэж нэрлэв хамгийн их цэг у \u003d f (x) функц, хэрэв бүх x тойргийнхоо тэгш бус байдал байвал. Хамгийн их цэг дэх функцийн утгыг нэрлэнэ хамгийн их функц тэмдэглэдэг.

Цэг гэж нэрлэв хамгийн бага цэг у \u003d f (x) функц, хэрэв бүх x тойргийнхоо тэгш бус байдал байвал. Хамгийн бага цэг дэх функцийн утгыг нэрлэнэ хамгийн бага функц тэмдэглэдэг.

Ойролцоох газар нь цэгүүд нь интервал гэсэн утгатай хангалттай бага эерэг тоо хаана байна.

Хамгийн бага ба дээд цэгүүдийг дууддаг экстремум цэгүүд, мөн экстремумын цэгүүдтэй тохирох функцийн утгыг нэрлэнэ экстрема функцууд.

Функцийн экстремаг функцын хамгийн том, хамгийн бага утгатай андуурч болохгүй.

Эхний зураг дээр интервал дахь функцийн хамгийн их утга нь максимум цэг дээр хүрч, функцийн хамгийн их утгатай тэнцүү байна, хоёр дахь зураг дээр функцийн хамгийн их утга нь x \u003d b-д хүрнэ, энэ нь хамгийн их цэг биш юм.

Функцийг нэмэгдүүлэх, бууруулах хангалттай нөхцөл.

Функцийн өсөлт, бууралтын хангалттай нөхцөл (шинж тэмдгүүд) дээр үндэслэн функцийн өсөлт, бууралтын интервалуудыг олно.

Интервал дахь функц нэмэгдэж, буурах шинж тэмдгүүдийн тайлбарыг энд оруулав.

y \u003d f (x) функцийн дериватив нь Х интервалаас ямар ч х-т эерэг байвал функц X дээр нэмэгдэнэ;
хэрэв y \u003d f (x) функцийн дериватив нь Х интервалаас ямар ч х сөрөг байвал уг функц X дээр буурна.

Тиймээс функцийн өсөлт, бууралтын интервалыг тодорхойлохын тулд дараахь зүйлийг хийх шаардлагатай болно.

Алгоритмыг тодруулахын тулд өсөн нэмэгдэж буй болон буурах функцүүдийн интервалуудыг олох жишээг авч үзье.

Нэг жишээ.

Өсөн нэмэгдэж буй болон буурах функцүүдийн интервалыг ол.

Шийдэл.

Эхний алхамд та функцийн цар хүрээг олох хэрэгтэй. Бидний жишээн дээр илэрхийлсэн илэрхийлэл арилах ёсгүй.

Бид үүсмэл функцийг хайж олох болно.

Өсгөх ба буурах функцийн интервалуудыг хангалттай шалгуураар тодорхойлохын тулд тодорхойлолтын чиглэл дэх тэгш бус байдлыг шийддэг. Бид интервалын аргыг ерөнхий байдлаар ашигладаг. Тоолуурын цорын ганц хүчинтэй үндэс нь x \u003d 2 байх бөгөөд хуваагч нь х \u003d 0-д алга болно. Эдгээр цэгүүд нь домэйныг интервал болгон задалж, функцийн үүсмэл нь тэмдгээ хадгалдаг. Бид эдгээр цэгүүдийг тоон мөрөнд тэмдэглэв. Илүүдэл ба хасах нь үүсмэл эерэг эсвэл сөрөг утгатай интервалыг дур зоргоороо илэрхийлнэ. Доорх сум нь функцийн харгалзах интервал дахь өсөлт эсвэл бууралтыг схемийн дагуу харуулна.

Ийм байдлаар ба .

Цэгт нь x \u003d 2, функц нь тодорхойлогддог ба тасралтгүй байх тул өсөлт, бууралтын аль алинд нь нэмэх хэрэгтэй. X \u003d 0 цэг дээр функц тодорхойлогдоогүй тул энэ цэг хүссэн интервалд ороогүй болно.

Бид олж авсан үр дүнг харьцуулах функцын графикийг өгдөг.

Хариулт нь:

Хэзээ функц нэмэгддэг , интервал дээр буурна (0; 2].

Функцийн экстремумын нөхцөл хангалттай.

Функцийн максимум ба минимумыг олохын тулд та экстремумын гурван шинж тэмдгийн аль нэгийг ашиглаж болно, мэдээжийн хэрэг, хэрэв функц нь тэдний нөхцлийг хангаж байвал. Хамгийн түгээмэл бөгөөд тохиромжтой нь тэдний эхнийх юм.

Экстремумын эхний хангалттай нөхцөл.

Y \u003d f (x) функцийг цэгийн ойролцоо байрлалаар ялгавартай байх ба тухайн цэг нь өөрөө тасралтгүй байх.

Өөрөөр хэлбэл:

Функцийн экстремумын эхний тэмдгээр экстремум цэгүүдийг олох алгоритм.

Бид функцийн тодорхойлолтын домэйныг олдог.
Бид функцийн деривативыг тодорхойлолтын домайн дээр олдог.
Тоолуурын тэг, деривативын нийлбэрийн тэгүүд ба үүсмэл байхгүй домэйны цэгүүдийг тодорхойлно (жагсаасан бүх цэгүүдийг нэрлэнэ боломжтой экстремумын цэгүүдэдгээр цэгүүдийг дамжин өнгөрөхөд үүсмэл нь зүгээр л тэмдгээ өөрчилж болно).
Эдгээр цэгүүд нь тухайн функц нь тухайн тэмдгийг хадгалдаг интервалд хуваана. Бид интервал бүр дээр деривативын шинж тэмдгийг тодорхойлдог (жишээлбэл, тухайн интервал дахь ямар ч цэг дээр функцийн деривативын утгыг тооцоолох).
Бид үйл ажиллагаа нь тасралтгүй үргэлжлэх цэгүүдийг сонгодог бөгөөд үүгээр дамжин үүсмэл өөрчлөлт өөрчлөгддөг. Эдгээр нь экстремумын цэгүүд юм.

Маш олон үгтэй бол функцын экстремумын анхны хангалттай нөхцлийг ашиглан функцын экстремум ба экстрема цэгүүдийг олох цөөн хэдэн жишээг авч үзэх нь дээр.

Нэг жишээ.

Функцийн экстремаг ол.

Шийдэл.

Функцийн домайн нь x \u003d 2-оос бусад бүх бодит тоонуудын багц юм.

Бид деривативыг олдог:

Тоолуурын тэгүүд нь x \u003d -1 ба x \u003d 5 цэгүүд, тоологч нь x \u003d 2-т алга болно. Эдгээр цэгүүдийг тоон тэнхлэг дээр тэмдэглээрэй.

Бид интервал тус бүрийн деривативын шинж тэмдгийг тодорхойлдог бөгөөд үүний тулд интервал бүрийн аль ч цэг дээр, жишээлбэл, x \u003d -2, x \u003d 0, x \u003d 3 ба x \u003d 6 цэгүүдэд деривативын утгыг тооцоолно.

Тиймээс үүсмэл нь интервал дээр эерэг байна (зураг дээр бид энэ интервал дээр нэмэх тэмдэг тавьдаг). Үүнтэй адил

Тиймээс, бид хоёр дахь завсарлагаас хасах, гурав дахь нь хасах, дөрөвдэхээс давсан утгыг тавьдаг.

Функц нь тасралтгүй үргэлжлэх ба түүний үүсмэл өөрчлөлтийн тэмдгийг сонгоход үлддэг. Эдгээр нь туйлын цэгүүд юм.

Цэгт нь x \u003d -1 функц нь тасралтгүй бөгөөд үүсмэл нь тэмдгээс хасах хүртэл өөрчлөгдөнө, иймээс экстремумын эхний тэмдгийн дагуу x \u003d -1 бол хамгийн их цэг, функцийн хамгийн дээд хэмжээ нь түүнд тохирно .

Цэгт нь x \u003d 5 функц нь тасралтгүй бөгөөд үүсмэл нь тэмдгээс хасах тэмдэг хүртэл өөрчлөгддөг, тэгэхээр x \u003d -1 нь хамгийн бага цэг, функцийн хамгийн бага хэмжээ нь түүнд тохирч байх болно .

График дүрслэл.

Хариулт нь:

ТӨЛБӨРГҮЙ ТӨЛБӨРГҮЙ: экстремумын эхний хангалттай шинж тэмдэг нь тухайн цэг дээр функцийн ялгаатай байдлыг шаарддаггүй.

Нэг жишээ.

Функцийн экстремум цэгүүд ба экстремумуудыг ол .

Шийдэл.

Функцийн домайн бол бодит тооны бүхэл бүтэн багц юм. Функцийг өөрөө дараах байдлаар бичиж болно.

Функцийн үүсмэл зүйлийг ол:

Цэгт нь x \u003d 0, үүсмэл зүйл байхгүй, учир нь аргумент тэг байх үед нэг талт хязгаарын утгууд давхцахгүй байна:

Үүний зэрэгцээ анхны функц нь x \u003d 0 дээр тасралтгүй байна (функцийг тасралтгүй шалгах хэсгийг үзнэ үү).

Үүсмэл зам нь алга болох аргументын утгыг олоорой.

Бид тоон мөрөнд олж авсан бүх цэгүүдийг тэмдэглэж, интервал тус бүр дээр үүсмэл тэмдгийг тодорхойлно. Үүний тулд бид деривативын утгыг интервал бүрийн дурын цэг дээр, жишээлбэл, тооцоолно x \u003d -6, x \u003d -4, x \u003d -1, x \u003d 1, x \u003d 4, x \u003d 6.

Энэ бол

Тиймээс, экстремумын эхний тэмдгийн дагуу хамгийн бага цэгүүд байна , хамгийн их оноо .

Бид тохирох minima функцийг тооцоолно

Бид тохирох maxima функцийг тооцоолно

График дүрслэл.

Хариулт нь:

Функцийн экстремумын хоёрдахь шинж тэмдэг.

Таны харж байгаагаар функцийн экстремумын энэ шинж тэмдэг нь тухайн цэг дээр дор хаяж хоёр дахь дараалал хүртэл үүсмэл үүсэхийг шаарддаг.

Функцийн өсөлт ба бууралт

функц у = е(х) хэсгийг сегмент дээр өсгөх гэж нэрлэдэг [ а, б] хэрэв ямар нэг хос байвал х ба x ", ба ≤ x тэгш бус байдал е(х) ≤ е (x "), мөн эрс нэмэгдэх - хэрэв тэгш бус байдал байвал е (х) е(x ") Функц буурах, хатуу буурах нь ижил төстэй байдлаар тодорхойлогддог. Жишээлбэл, функц үед = х 2 (инжир. , a) сегмент дээр эрс нэмэгддэг ба

(инжир. , b) энэ сегмент дээр эрс буурч байна. Өсөн нэмэгдэж буй функцуудаар тэмдэглэгдсэн байна е (х), буурч байна е (х) ↓. Функцийг ялгахын тулд е (х) сегмент дээр нэмэгдэж байсан [ гэхдээ, б], энэ нь түүний үүсмэл байх шаардлагатай бөгөөд хангалттай юм е"(х) сөрөг биш байсан [ гэхдээ, б].

Сегмент дээрх функцийн өсөлт, бууралттай зэрэгцэн тухайн цэг дэх функцийн өсөлт, бууралтыг тооцно. Чиг үүрэг үед = е (х) цэг дээр нэмэгдэх гэж нэрлэдэг х 0 бол цэгийг агуулсан ийм интервал (α, β) байвал х 0 ямар ч цэг дээр х аас (α, β) х\u003e х 0, тэгш бус байдал е (х 0) ≤ е (х), мөн ямар ч цэг дээр ашиглах боломжтой х аас (α, β) x 0, тэгш бус байдал е (х) ≤ е (х 0). Үүний нэгэн адил, тухайн цэг дэх функцийг эрс нэмэгдүүлдэг х 0. Хэрэв е"(х 0) > 0, дараа нь функц е(х) цэг дээр эрс нэмэгддэг х 0. Хэрэв е (х) интервалын цэг бүрт нэмэгддэг ( а, б), дараа нь энэ интервалд нэмэгдэх болно.

S. B. Stechkin.

ЗХУ-ын агуу нэвтэрхий толь бичиг. - М .: Зөвлөлтийн нэвтэрхий толь бичиг. 1969-1978 .

Бусад толь бичгүүдийн "Функцыг нэмэгдүүлэх, багасгах" гэж юу болохыг үзээрэй

Математик анализын тухай ойлголтууд. F (x) функцийг ӨӨРИЙН ХҮЧНИЙ ХҮЧНИЙ ХУВИЙН сегмент дээр нэмэгдэж буй янз бүрийн насны хүн амын тооны харьцаа гэж нэрлэдэг. Төрөлт, нас баралтын түвшин, хүмүүсийн дундаж наслалтаас хамаарна ... Том нэвтэрхий толь бичиг

Математик анализын тухай ойлголтууд. F (x) функцийг хэрвээ x1 ба x2 цэгүүдийн хувьд a≤x1 ... байвал сегмент дээр өсгөх гэж нэрлэдэг. Нэвтэрхий толь бичиг

Математикийн тухай ойлголтууд. шинжилгээ хийх. F (x) функц гэж нэрлэдэг x1 ба x2 цэгүүдийн хослолын хувьд [a, b] сегмент дээр нэмэгдэх ба<или=х1 <х<или=b, выполняется неравенство f(x1)Байгалийн түүх. Нэвтэрхий толь бичиг

Функцийн дериватив ба дифференциалуудыг судалж, функцийг судлахад ашигладаг математикийн салбар. Дизайн D. ба. бие даасан математикийн хичээлийг I. Ньютон, Г.Лейбниц нарын нэрээр (17-р сарын 2-ны хагас ... ЗХУ-ын агуу нэвтэрхий толь бичиг

Дериватив ба дифференциал гэсэн ойлголтуудыг судалж, функцийг судлахдаа ашиглах аргууд болох математикийн хэсэг. D.-ийн хөгжил ба. интеграл тооцоог боловсруулахтай нягт холбоотой. Салшгүй бөгөөд тэдгээрийн агуулга. Тэд хамтдаа үндсийг бүрдүүлдэг ... ... Математикийн нэвтэрхий толь бичиг

Энэ нэр томъёо нь өөр утгатай, функцийг үзнэ үү. "Дэлгэц" гэсэн хүсэлтийг энд дахин чиглүүлсэн; бусад утгыг үзнэ үү ... Wikipedia

Аристотель ба перипатетик - Аристотелийн асуулт Аристотель Аристотелийн амьдрал 384/383 онд төрсөн. МЭӨ э. Македониятай хиллэдэг Стагира хотод. Түүний аав Никтомус Македони улсын хаан Филиппийн аав Аминтосын үйлчлэлд эмч байжээ. Гэр бүлийнхэнтэйгээ хамт залуу Аристотель ... ... Барууны философи нь гарал үүслээс өнөөг хүртэл

- (QCD), квантын дүр төрхөөр бүтээгдсэн кварк ба глюоны хүчтэй үйлдлийн квант талбайн онол. электродинамик (QED) хэмжигдэхүүнийг "өнгөт" хэмжигдэхүүн. QED-ээс ялгаатай нь QCD дахь ферми нь нэмэлт тэжээлтэй байдаг. эрх чөлөөний зэрэг. дугаар, ... ... Физик нэвтэрхий толь

I зүрх Зүрх (лат. Кор, грек. Cardia) нь шахуургын үүрэг гүйцэтгэж, цусны эргэлтийн тогтолцоонд цусны хөдөлгөөнийг хийдэг хөндий фибро-булчингийн эрхтэн юм. Анатоми Зүрх нь перикардийн доторхи дунд медиастинум (Mediastinum) дотор байдаг ... ... Анагаах ухааны нэвтэрхий толь бичиг

Ургамлын амьдрал нь бусад амьд организмын нэгэн адил харилцан уялдаатай процессын цогц юм; тэдгээрийн хамгийн чухал нь хүрээлэн буй орчинтой бодисын солилцоо гэдэг нь мэдэгдэж байна. Байгаль орчин бол хаанаас ... Биологийн нэвтэрхий толь бичиг

Хэт их функцууд

Тодорхойлолт 2

$ X_0 $ цэг нь $ f (x) \\ le f (x_0) $ тэгш бус байдлыг харуулсан $ f (x) $ функцийн хамгийн их цэг гэж нэрлэв.

Тодорхойлолт 3

$ X_0 $ цэгийг $ f (x) $ функцийн хамгийн их цэг гэж нэрлэнэ. Хэрэв энэ ойролцоо байгаа бүх $ x $ -ийн хувьд $ f (x) \\ ge f (x_0) $ тэгш бус байдал байгаа бол энэ цэгийн ойролцоо байна.

Функцийн экстремум гэсэн ойлголт нь функцийн эгзэгтэй цэг гэсэн ойлголттой нягт холбоотой байдаг. Бид түүний тодорхойлолтыг танилцуулж байна.

Тодорхойлолт 4

$ x_0 $ -ийг $ f (x) $ функцийн эгзэгтэй цэг гэж нэрлэвэл:

1) $ x_0 $ нь тодорхойлолт домэйны дотоод цэг юм;

2) $ f "\\ зүүн (x_0 \\ баруун) \u003d 0 $ эсвэл байхгүй.

Экстремумын тухай ойлголтын хувьд түүний оршин тогтноход шаардлагатай, шаардлагатай нөхцлийн тухай теоремуудыг томъёолж болно.

Теорем 2

Экстремумын хангалттай нөхцөл

$ X_0 $ цэг нь $ y \u003d f (x) $ функцэд чухал ач холбогдолтой бөгөөд $ (a, b) $ интервалд оршино. $ \\ Зүүн (a, x_0 \\ баруун) \\ ба \\ (x_0, b) $ хоорондох $ f "(x) $ хэмээх интервал бүрт тогтмол тэмдэг хадгална гэж бодъё.

1) Хэрэв $ (a, x_0) $ интервал дээр $ f "\\ зүүн (x \\ баруун)\u003e 0 $, $ (x_0, b) $ интервал дээр $ f" \\ зүүн (x \\ баруун) байна

2) Хэрэв $ (a, x_0) $ интервал дээр $ f "\\ left (x \\ right) 0 $ байвал уг функцийн хамгийн бага цэг бол $ x_0 $ болно.

3) $ (a, x_0) $ интервал дээр, $ (x_0, b) $ интервал дээр $ f "\\ зүүн (x \\ баруун)\u003e 0 $ эсвэл" $ f "\\ зүүн (x \\ баруун) үүсмэл бүтээгдэхүүн байвал

Энэ теоремыг 1-р зурагт үзүүлэв.

Зураг 1. Экстрема үүсэх хангалттай нөхцөл

Хэт их жишээ (Зураг 2).