세트 이론의 요소를 설정합니다. 세트 작업
토폴로지에 대해 언제 처음 배웠는지 기억이 나지 않지만 이 과학은 즉시 관심을 갖게 되었습니다. 찻주전자는 도넛으로 변하고 구체는 뒤집힙니다. 많은 사람들이 그것에 대해 들었습니다. 그러나 더 심각한 수준에서 이 주제를 탐구하려는 사람들은 종종 어려움을 겪습니다. 본질적으로 매우 추상적 인 가장 기본적인 개념을 마스터하는 경우 특히 그렇습니다. 더욱이, 많은 출처는 의도적으로 독자를 혼란스럽게 하려는 것 같습니다. 러시아 위키가 토폴로지가 하는 일에 대한 매우 모호한 공식을 제공한다고 가정해 봅시다. 연구하는 학문이라고 합니다 위상 공간. 위상 공간에 대한 글에서 독자는 위상 공간이 다음을 갖춘 공간임을 알 수 있습니다. 토폴로지. Lemov의 무덤 스타일의 그러한 설명은 실제로 주제의 본질을 명확히하지 않습니다. 더 명확한 형태로 주요 기본 개념을 설명하려고 노력할 것입니다. 내 메모에는 변형되는 찻주전자와 베이글은 없지만 결국 이 마법을 배울 수 있는 첫 번째 단계가 취해질 것입니다.
하지만 저는 수학자도 아니고 100% 인본주의자이기 때문에 아래에 적힌 내용이 거짓말일 가능성도 충분히 있습니다! 글쎄, 적어도 그것의 일부.
나는 인도주의적 친구들을 위해 토폴로지에 관한 일련의 기사의 시작으로 이 노트를 처음 썼지만 아무도 그것을 읽기 시작하지 않았습니다. 수정 및 확장 버전을 Habr에 게시하기로 결정했습니다. 여기에서이 주제에 대해 어느 정도 관심이있는 것 같았고 아직 이런 종류의 기사가 없었습니다. 오류 및 부정확성에 대한 모든 의견에 미리 감사드립니다. 사진을 많이 사용하니 주의하세요.
집합 이론에 대한 간략한 요약부터 시작하겠습니다. 대부분의 독자가 익숙하다고 생각하지만 그럼에도 불구하고 기본 사항을 상기시켜 드리겠습니다.
따라서 세트에는 정의가 없으며 우리는 그것이 무엇인지 직관적으로 이해한다고 믿어집니다. Kantor는 다음과 같이 말했습니다. 물론 이것은 수학적 정의가 아니라 알레고리적 설명일 뿐입니다.
집합론은 많은 놀라운 역설로 알려져 있습니다. 예를 들어 . 20세기 초 수학의 위기와도 연결된다.
집합 이론은 ZFC 또는 NBG 등과 같은 여러 변형에 존재합니다. 이론의 변형은 프로그래머에게 매우 중요한 유형 이론입니다. 마지막으로 일부 수학자들은 Habré에 대해 많이 쓰여진 집합 이론 대신 범주 이론을 수학의 기초로 사용할 것을 제안합니다. 유형 이론과 집합 이론은 수학적 객체를 "내부에서" 설명하는 반면 범주 이론은 내부 구조에 관심이 없고 상호 작용 방식에만 관심이 있습니다. "외부"특성을 제공합니다.
우리에게는 집합론의 아주 기본적인 토대만이 중요합니다.
세트는 유한합니다.
끝이 없습니다. 예를 들어 문자 ℤ(또는 키보드에 둥근 문자가 없는 경우 Z만)로 표시되는 정수 집합입니다.

마지막으로 빈 세트가 있습니다. 그것은 전체 우주에서 정확히 하나입니다. 이 사실에 대한 간단한 증거가 있지만 여기서는 제공하지 않겠습니다.

집합이 무한이면 발생합니다. 셀 수 있는. 셀 수 있는 - 요소가 자연수로 다시 번호를 매길 수 있는 집합입니다. 자연수 집합 자체도 셀 수 있습니다. 다음은 정수를 열거하는 방법입니다.

유리수를 사용하면 더 어렵지만 번호를 매길 수도 있습니다. 이 방법은 대각선 과정그리고 아래 그림처럼 보입니다.

1부터 시작하여 유리수를 통해 지그재그로 이동합니다. 동시에 우리가 얻은 각 숫자에 짝수를 할당합니다. 음의 유리수는 같은 방식으로 계산되며 숫자만 홀수이며 3부터 시작합니다. 전통적으로 0은 첫 번째 숫자를 가져옵니다. 따라서 모든 유리수에 번호를 매길 수 있음이 분명합니다. 4.87592692976340586068 또는 1.00000000000001 또는 -9092 또는 42와 같은 모든 숫자는 이 표에서 해당 번호를 얻습니다. 그러나 모든 숫자가 여기에 포함되는 것은 아닙니다. 예를 들어 √2는 숫자를 얻지 못합니다. 한때 이것은 그리스인들을 크게 화나게했습니다. 무리수를 발견한 사람이 익사했다고 합니다.
집합 크기 개념의 일반화는 다음과 같습니다. 힘. 유한 세트의 카디널리티는 해당 요소의 수와 같습니다. 무한 집합의 카디널리티는 인덱스가 있는 히브리 문자 알레프로 표시됩니다. 가장 작은 무한한 힘은 힘입니다 ℵ 0 . 셀 수 있는 집합의 카디널리티와 같습니다. 그러므로 우리가 보는 바와 같이 자연수는 정수나 유리수만큼 많습니다. 이상하지만 사실입니다. 다음은 파워 연속체. 작은 고딕 문자 c로 표시됩니다. 예를 들어 이것은 실수 집합 ℝ의 카디널리티입니다. 연속체의 힘이 힘과 같다는 가설이 있습니다. ℵ 1 . 즉, 이것이 가산 집합의 카디널리티 이후의 다음 카디널리티이고, 가산 집합과 연속체 사이에 중간 카디널리티가 없다는 것입니다.
세트에서 다양한 작업을 수행하고 새 세트를 가져올 수 있습니다.
1. 세트를 조합할 수 있습니다.


3. 집합의 교집합을 검색할 수 있습니다.

실제로 이것은 이 노트의 목적을 위해 알아야 할 세트에 관한 것입니다. 이제 토폴로지 자체로 진행할 수 있습니다.
토폴로지는 특정 구조로 집합을 연구하는 과학입니다. 이 구조를 토폴로지라고도 합니다.
비어 있지 않은 집합 S를 가집시다.
이 집합이 우리가 T라고 부르는 집합을 사용하여 기술되는 어떤 구조를 가지도록 합시다. T는 다음과 같은 집합 S의 부분집합 집합입니다.
1. S 자체와 ∅는 T에 속합니다.
2. 요소 T의 임의의 패밀리 조합은 T에 속합니다.
3. 임의의 교집합 결정적인요소 계열 T의 T는 T에 속합니다.
이 세 점이 유지되면 구조는 집합 S에서 T의 토폴로지입니다. 집합 T의 요소는 다음과 같습니다. 열려 있는토폴로지 T에서 S에 대한 집합입니다. 열린 집합에 대한 보완은 다음과 같습니다. 닫은설정합니다. 세트가 열려 있다고 해서 닫히지 않았다는 의미는 아니며 그 반대도 마찬가지입니다. 또한 주어진 집합에서 일부 토폴로지와 관련하여 열려 있지도 닫혀 있지도 않은 하위 집합이 있을 수 있습니다.
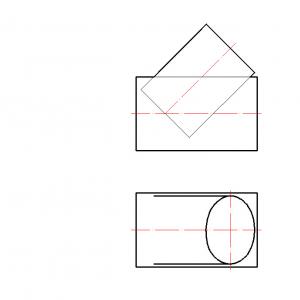
예를 들어 보겠습니다. 세 개의 색상이 있는 삼각형으로 구성된 집합이 있다고 가정합니다.

가장 간단한 토폴로지는 반이산 토폴로지. 여기 있습니다.

이 토폴로지는 토폴로지라고도 합니다. 스티커 도트. 세트 자체와 빈 세트로 구성됩니다. 이것은 실제로 토폴로지의 공리를 만족시킵니다.
한 세트에 여러 토폴로지를 정의할 수 있습니다. 여기에 발생하는 또 다른 매우 원시적인 토폴로지가 있습니다. 이산이라고 합니다. 주어진 집합의 모든 하위 집합으로 구성된 토폴로지입니다.

다음은 토폴로지입니다. 그것은 내가 글자로 표시한 7개의 다색 별 S 세트에 주어집니다. 토폴로지인지 확인하십시오. 확실하지 않습니다. 갑자기 어떤 종류의 조합이나 교차로를 놓쳤습니다. 이 그림에는 집합 S 자체, 빈 집합, 토폴로지의 다른 모든 요소의 교집합 및 합집합도 포함되어야 합니다.

쌍토폴로지와 주어진 세트에서 위상 공간.

세트에 많은 포인트가 있는 경우(무한히 많은 포인트가 있을 수 있다는 사실은 말할 것도 없고) 모든 열린 세트를 나열하는 것은 문제가 될 수 있습니다. 예를 들어, 3개의 요소 집합에 대한 개별 토폴로지의 경우 8개의 집합 목록을 만들어야 합니다. 그리고 4개 요소 세트의 경우 불연속 토폴로지는 이미 16개, 5 - 32개, 6 - 64개 등을 갖습니다. 모든 열린 집합을 열거하지 않기 위해 일종의 약식 표기법이 사용됩니다. 이러한 요소는 작성되며, 그 조합은 모든 열린 집합을 제공할 수 있습니다. 그것은이라고 베이스토폴로지. 예를 들어, 3개의 삼각형으로 구성된 이산 공간 토폴로지의 경우 삼각형을 결합하면 이 토폴로지의 다른 모든 열린 집합을 얻을 수 있기 때문에 별도로 취한 3개의 삼각형이 됩니다. 베이스는 토폴로지를 생성한다고 합니다. 요소가 베이스를 생성하는 집합을 프리베이스라고 합니다.
아래는 5개의 별 집합에 대한 이산 토폴로지의 기본 예입니다. 보시다시피 이 경우 기본은 5개의 요소로 구성되어 있지만 토폴로지는 최대 32개의 하위 집합으로 구성됩니다. 베이스를 사용하여 토폴로지를 설명하는 것이 훨씬 더 편리합니다.

공개 세트는 무엇입니까? 어떤 의미에서 그들은 포인트 사이의 "근접성"과 그 차이에 대한 아이디어를 제공합니다. 점이 두 개의 서로 다른 열린 집합에 속하거나 한 점이 다른 것을 포함하지 않는 열린 집합에 있는 경우 위상적으로 다릅니다. 반이산 토폴로지에서 모든 점은 이러한 의미에서 구별할 수 없으며 함께 붙어 있는 것처럼 보입니다. 반대로 이산 토폴로지에서는 모두포인트가 다릅니다.
열린 집합의 개념은 개념과 불가분의 관계가 있습니다. 이웃. 일부 저자는 열린 집합이 아니라 이웃의 관점에서 토폴로지를 정의합니다. 점 p의 이웃은 이 점을 중심으로 하는 열린 공을 포함하는 집합입니다. 예를 들어, 아래 그림은 점의 이웃과 비이웃을 보여줍니다. 집합 S 1은 점 p의 이웃이지만 집합 S 2는 그렇지 않습니다.

열린 집합과 octestity의 관계는 다음과 같이 공식화할 수 있습니다. 열린 집합은 각 요소가 주어진 집합에 있는 이웃을 갖는 그러한 집합입니다. 또는 그 반대의 경우, 세트가 해당 포인트의 이웃인 경우 세트가 열려 있다고 말할 수 있습니다.
이 모든 것이 토폴로지의 가장 기본적인 개념입니다. 여기에서 구체를 뒤집는 방법은 아직 명확하지 않습니다. 아마도 앞으로는 이런 종류의 주제에 접근할 수 있을 것입니다.
UPD. 내 연설의 부정확성으로 인해 세트의 카디널리티에 대해 약간의 혼란이 있었습니다. 내 텍스트를 약간 수정했으며 여기에 설명을 제공하고 싶습니다. 집합 이론을 만든 Kantor는 무한 집합을 비교할 수 있는 카디널리티 개념을 도입했습니다. Cantor는 셀 수 있는 집합(예: 유리수)과 연속체(예: 실수)의 카디널리티가 다르다는 것을 확립했습니다. 그는 연속체의 카디널리티가 셀 수 있는 집합의 카디널리티 다음에 있다고 제안했습니다. 알레프 1과 같습니다. Cantor는 이 추측을 증명하려고 시도했지만 성공하지 못했습니다. 나중에 이 가설이 반증될 수도 증명될 수도 없다는 것이 분명해졌습니다.
집합의 개념은 엄격하게 정의되지 않은 원래의 개념입니다. 다음은 G. Cantor에 속하는 세트(보다 정확하게는 세트 아이디어에 대한 설명)의 정의입니다. 하나, 즉 하나의 법칙에 의해 하나의 전체로 연결될 수 있는 특정 요소들의 집합."
일반적으로 세트는 라틴 알파벳의 대문자로 표시되고 해당 요소는 소문자로 표시되지만 특정 세트의 요소가 다른 세트일 수 있기 때문에 때때로 이 규칙에서 벗어나야 합니다. 요소 a가 세트에 속한다는 사실은 로 쓰여집니다.
수학에서는 다양한 집합을 다룹니다. 이러한 집합의 요소에 대해 상수와 변수라는 두 가지 주요 표기법을 사용합니다.
범위가 있는 개별 상수(또는 상수)는 집합의 고정 요소를 나타냅니다. 예를 들어 실수의 지정(특정 숫자 체계의 레코드)이 있습니다. 두 개의 상수와 값의 범위에 대해 쓸 것입니다 , 이것에 의해 표시된 세트의 요소의 일치를 의미합니다.
범위가 있는 개별 변수(또는 그냥 변수)는 집합의 미리 결정된 요소가 아니라 임의의 것을 나타냅니다. 이 경우 변수가 세트를 통해 실행되거나 변수가 세트에서 임의의 값을 취한다고 말합니다. 를 써서 변수의 값을 고정할 수 있습니다. 여기서 는 와 같은 범위의 상수입니다. 이 경우 변수 대신 특정 값이 대체되었거나 대신 대체되었거나 변수가 값을 취했다고 말합니다.
변수의 동등성은 다음과 같이 이해됩니다. 변수가 임의의 값을 가질 때마다 변수는 동일한 값을 가지며 그 반대도 마찬가지입니다. 따라서 동일한 변수는 "동기적으로" 항상 동일한 값을 사용합니다.
일반적으로 범위가 특정 숫자 집합, 즉 집합 중 하나인 상수 및 변수 및 는 각각 자연, 정수(또는 정수), 유리수, 실수 및 복소수 상수 및 변수라고 합니다. 이산 수학 과정에서 우리는 다양한 상수와 변수를 사용할 것이며 그 범위는 항상 숫자 집합이 아닙니다.
기록을 단축하기 위해 논리적 기호를 사용하여 공식과 같이 문장을 간략하게 작성할 수 있습니다. 발화의 개념이 정의되어 있지 않습니다. 모든 진술이 참 또는 거짓일 수 있음을 나타냅니다(물론 동시에 둘 다!).
집합에 대한 논리 연산(바인딩)
기존 문장에서 새로운 문장을 형성하기 위해 다음과 같은 논리 연산(또는 논리 연결)이 사용됩니다.
1. 분리: 진술(읽기: "또는")은 진술 중 적어도 하나가 참인 경우에만 참입니다.
2. 접속사: 명제(읽기: "and")는 명제와 둘 다 참인 경우에만 참입니다.
3. 부정: 진술(읽기: "not")은 거짓인 경우에만 참입니다.
4. 암시: 진술(읽기: "if, then" 또는 "implies")은 진술이 참이거나 두 진술이 모두 거짓인 경우에만 참입니다.
5. 동등성(또는 동등성): 진술(읽기: "if and only if")은 두 진술이 동시에 참이거나 동시에 거짓인 경우에만 참입니다. 참인 두 개의 진술은 논리적으로 동등하거나 동등하다고 합니다.
논리 연산을 사용하여 문장을 작성할 때 모든 연산이 수행되는 순서는 괄호의 배열에 의해 결정된다고 가정합니다. 표기법을 단순화하기 위해 특정 연산 순서를 허용하면서 괄호를 생략하는 경우가 많습니다("우선 순위 규칙").
부정 연산자는 항상 먼저 수행되므로 괄호로 묶지 않습니다. 두 번째는 결합, 분리, 마지막으로 함축과 등가의 연산을 수행합니다. 예를 들어 다음과 같은 문장이 작성됩니다. 이 진술은 두 진술의 분리입니다. 첫 번째는 부정이고 두 번째는입니다. 대조적으로, 명제는 명제와 의 분리의 부정입니다.
예를 들어, 우선 순위에 따라 괄호를 넣은 후의 진술은 다음과 같은 형식을 취합니다.
위에서 소개한 논리적 접속사에 대해 몇 가지 논평을 해보자. 이접, 접속, 부정의 의미있는 해석은 특별한 설명이 필요하지 않습니다. 의미는 정의에 따라 명제가 참이고(진리와 관계없이) 둘 다 거짓일 때마다 참입니다. 따라서 함축이 참이면 참일 때 참이 발생하지만 그 반대는 참이 아닐 수 있습니다. 거짓인 경우 진술은 참 또는 거짓일 수 있습니다. 이것은 "if , then"의 형태로 의미를 읽는 동기를 부여합니다. 또한 명제는 명제와 동일하므로 "if, then"이 "not or"와 동일시된다는 것을 이해하기 쉽습니다.
동등성은 "양면 함축"에 지나지 않습니다. 에 해당합니다. 이것은 진리에서 진리가 나오고, 반대로 진리는 진리에서 나온다는 뜻입니다.
예 1.1.복잡한 진술의 참 또는 거짓을 결정하기 위해 포함된 진술의 참 또는 거짓에 따라 진리표가 사용됩니다.
테이블의 처음 두 열에는 명령문과 취할 수 있는 모든 가능한 값 세트가 포함됩니다. 진술의 진실은 문자 "I"또는 숫자 1로 표시되고 허위는 문자 "L"또는 숫자 0으로 표시됩니다. 나머지 열은 왼쪽에서 오른쪽으로 채워집니다. 따라서 각 값 세트에 대해 해당 명령문 값을 찾으십시오.
논리 연산의 진리표는 가장 단순한 형태를 가집니다(표 1.1-1.5).
복잡한 진술을 생각해 봅시다. 계산의 편의를 위해 명제를 로, 명제를 로 표기하고 원래 명제를 로 표기한다. 이 진술의 진리표는 열과 (표 1.6)로 구성됩니다.
술어 및 한정사
복합문은 논리적 연결을 통해서만 형성되는 것이 아니라 술어와 한정사를 통해서도 형성됩니다.
술어는 하나 이상의 개별 변수를 포함하는 명령문입니다. 예를 들어, "짝수가 있습니다" 또는 "1999년에 입학한 Bauman의 이름을 딴 모스크바 주립 공대 학생이 있습니다". 첫 번째 술어에는 정수 변수가 있고 두 번째 술어에는 "인간 개인" 집합을 통해 실행되는 변수가 있습니다. 여러 개별 변수를 포함하는 술어의 예는 다음과 같습니다. 술어는 주어진 술어에 포함된 모든 변수가 괄호 안에 나열되어 있다고 가정하여 형식으로 작성됩니다.
술어에 포함된 각 변수에 대해 특정 값을 대체합니다. 해당 값 범위를 가진 일부 상수가있는 값을 고정하면 변수를 포함하지 않는 명령문을 얻습니다. 예를 들어 "2는 짝수입니다", "Isaac Newton은 1999년에 입학한 Bauman의 이름을 딴 모스크바 주립 기술 대학의 학생입니다", "Ivanov는 Petrov의 아들입니다", "5는 7로 나눌 수 있습니다", 등. 이렇게 얻은 진술이 참인지 거짓인지에 따라 술어는 변수 값 집합에서 만족되거나 만족되지 않는다고 합니다. 포함된 변수 집합에 대해 만족하는 술어는 동일하게 참이라고 하고 변수의 값 집합에 대해 만족하지 않는 술어는 동일하게 거짓이라고 합니다.
술어의 진술은 변수 값을 대체하는 것뿐만 아니라 양화사를 통해서도 얻을 수 있습니다. 존재와 보편성이라는 두 가지 한정사를 소개합니다. 각각 및로 표시됩니다.
명제("집합의 모든 요소에 대해 참" 또는 간단히 "모두에 대해 참")는 조건자가 변수의 모든 값에 대해 참인 경우에만 정의에 따라 참입니다.
진술 ( "참인 세트의 요소가 있거나 있습니다", 또한 "일부는 참입니다")는 술어가 다음의 일부 값에서 충족되는 경우에만 정의에 따라 참입니다. 변수.
조건자 변수를 한정 기호와 연결
술어에서 수량사를 통해 문장이 형성될 때 술어의 변수가 수량사에 묶여 있다고 합니다. 마찬가지로 변수는 여러 변수를 포함하는 술어에 바인딩됩니다. 일반적인 경우, 형식의 표현
여기서 한정 기호 또는는 인덱스가 있는 각 문자를 대체할 수 있습니다.
예를 들어, 진술은 다음과 같습니다. "모든 사람에게 사실이 있습니다." 술어의 변수를 통해 실행되는 집합이 고정된 경우("기본적으로"를 의미) 수량어는 축약된 형식으로 작성됩니다. 또는 .
많은 수학적 정리는 방금 주어진 한정 기호가 있는 명령문과 유사한 형식으로 작성될 수 있습니다. 예를 들면 다음과 같습니다. 요점".
집합을 지정하는 방법
논리적 상징주의 사용의 특징을 논의한 후 집합에 대한 고려로 돌아가 보겠습니다.
두 세트는 세트의 요소가 세트의 요소이고 그 반대의 경우 동일한 것으로 간주됩니다. 집합이 요소에 의해 완전히 결정된다는 것은 위의 등집합 정의에 따른 것입니다.
구체적인 집합을 지정하는 방법을 고려해 보겠습니다. 원소의 수가 상대적으로 적은 유한집합의 경우 원소를 직접 열거하는 방법을 사용할 수 있다. 유한 집합의 요소는 임의의 고정된 순서로 중괄호 안에 나열됩니다. 우리는 집합이 요소에 의해 완전히 결정되기 때문에 유한 집합을 지정할 때 요소가 나열되는 순서는 중요하지 않다는 점을 강조합니다. 따라서 항목 등 모두 동일한 집합을 정의합니다. 또한 때로는 집합 표기에 요소의 반복이 사용됩니다. 항목이 항목과 동일한 집합을 정의한다고 가정합니다.
일반적인 경우 유한 집합의 경우 표기법이 사용됩니다. 원칙적으로 요소의 반복은 피합니다. 그런 다음 표기법에 의해 주어진 유한 집합은 요소로 구성됩니다. n-요소 집합이라고도 합니다.
그러나 요소를 직접 열거하여 집합을 지정하는 방법은 유한 집합의 매우 좁은 범위에 적용할 수 있습니다. 구체적인 집합을 지정하는 가장 일반적인 방법은 설명된 집합의 모든 요소가 가져야 하는 몇 가지 속성을 지정하는 것입니다.
이 아이디어는 다음과 같은 방식으로 구현됩니다. 범용 집합이라고 하는 일부 집합에 대해 변수 범위를 설정합니다. 요소가 집합의 요소이기도 한 이러한 집합만 고려한다고 가정합니다. 이 경우 주어진 집합의 요소만이 갖는 속성은 변수가 집합에서 임의의 값을 취하는 경우에만 실행되는 술어를 통해 표현될 수 있습니다. 즉, 개별 상수가 로 대체되는 경우에만 참입니다.
이 경우 술어는 집합의 특성 술어라고 하며 이 술어의 도움으로 표현되는 속성을 특성 속성 또는 집단화 속성이라고 합니다.
특성 술어를 통해 정의된 집합은 다음 형식으로 작성됩니다.
예를 들어, "각각의 자연수가 짝수인 모든 원소로 구성된 집합이 있다"는 의미입니다.
"집합 재산"이라는 용어는 이 속성을 통해 이질적인 요소를 하나의 전체로 수집할 수 있다는 사실에서 비롯되었습니다. 따라서 집합을 정의하는 속성(아래 참조)은 문자 그대로 일종의 "집단"을 형성합니다.
집합에 대한 Cantor의 정의로 돌아가면 집합의 특성 술어는 요소 집합이 하나의 전체로 결합되는 법칙입니다. 집단화 속성을 지정하는 술어는 동일하게 거짓일 수 있습니다. 이런 방식으로 정의된 집합에는 요소가 없습니다. 이를 공집합이라고 하며 로 표시합니다.
대조적으로, 동일하게 참인 특성 술어는 보편적인 집합을 정의합니다.
모든 술어가 집단화 속성을 표현하는 것은 아닙니다.
비고 1.1.보편적 집합 개념의 구체적인 내용은 우리가 집합론적 아이디어를 적용하는 특정 맥락에 의해 결정됩니다. 예를 들어, 다양한 숫자 집합만 다루는 경우 모든 실수 집합이 보편적인 집합으로 나타날 수 있습니다. 수학의 각 분야는 상대적으로 제한된 집합 집합을 다룹니다. 따라서 이러한 각 집합의 요소는 또한 그들을 "포괄하는" 일부 범용 집합의 요소라고 가정하는 것이 편리합니다. 범용 집합을 고정함으로써 수학적 추론에 나타나는 모든 변수와 상수의 값 범위를 고정합니다. 이 경우 수량사에 묶인 변수를 통해 실행되는 집합을 수량사에 표시하지 않는 것이 정확하게 가능합니다. 다음에서는 구체적인 범용 집합의 다양한 예를 만날 것입니다.
정의 1.많은어떤 - 또는 속성에 따라 하나의 전체로 통합된 일부 개체의 모음입니다.
집합을 구성하는 개체를 집합이라고 합니다. 강요.
그들은 라틴 알파벳의 대문자로 표시됩니다. ㅏ, 비, …, 엑스, 와이, ... 및 해당 요소는 해당 대문자로 표시됩니다. 가, 나, …, 엑스, 와이.
정의 1.1.어떤 원소도 포함하지 않는 집합을 호출 비어 있는기호 Ø로 표시됩니다.
집합은 열거와 설명으로 지정할 수 있습니다.
예:; ![]() .
.
정의 1.2.많은 ㅏ 하위 집합이라고 함 비세트의 각 요소가 ㅏ집합의 요소입니다 비. 이것을 상징적으로 표현하면 다음과 같습니다. AB (ㅏ에 포함된 비).
정의 1.3.두 세트 ㅏ그리고 비~라고 불리는 동일한, 동일한 요소로 구성된 경우 :( ㅏ =비).
세트 작업.
정의 1.4.합집합 또는 집합의 합 ㅏ그리고 비요소로 구성된 집합이며 각 요소는 이러한 집합 중 적어도 하나에 속합니다.
집합의 합집합은 다음과 같이 표시됩니다. AB(또는 ㅏ +비). 간단히 말해서, 쓸 수 있습니다 AB = .
AB= ㅏ +비
만약에 학사, 저것 ㅏ +B=A


정의 1.5.집합의 교집합 또는 곱 ㅏ그리고 비각각이 집합에 속하는 요소들로 구성된 집합이라고 합니다. ㅏ그리고 많은 비 동시에. 집합의 교집합은 다음과 같이 표시됩니다. AB(또는 ㅏ· 비). 간단히 말해서 다음과 같이 작성할 수 있습니다.
AB= ![]() .
.
AB =ㅏ · 비
만약에 비 ㅏ, 저것 ㅏ · 비=비


정의 1.6.차이 설정 ㅏ그리고 비세트가 호출되고 각 요소는 세트의 요소입니다. ㅏ
집합의 요소가 아닙니다. 비. 집합의 차이는 다음과 같이 표시됩니다. ㅏ\비. A-선발 ㅏ\비
=
![]() .
.
ㅏ\비 = ㅏ–비

요소가 숫자인 집합을 호출합니다. 숫자.
숫자 집합의 예는 다음과 같습니다.
N
=![]() 자연수의 집합입니다.
자연수의 집합입니다.
지= - 정수 집합.
큐=![]() 유리수의 집합입니다.
유리수의 집합입니다.
아르 자형실수의 집합입니다.
한 무리의 아르 자형유리수와 무리수를 포함합니다. 모든 유리수는 유한 소수점 분수 또는 무한 주기적 분수로 표현됩니다. 따라서 ;…은 유리수입니다.
무리수는 무한 비주기적 소수로 표현됩니다. 따라서 = 1.41421356...; = 3.14159265....는 무리수입니다.
케이(형식의 복소수 집합입니다. 지=ㅏ+ 바이)
아르 자형케이
정의 1.7.Ɛ ‒ 점의 이웃 엑스 0은 대칭 간격( 엑스 0 – Ɛ; 엑스 0 + Ɛ) 마침표 포함 엑스 0 .
특히, 간격( 엑스 0 –Ɛ; 엑스 0 +Ɛ), 부등식 엑스 0 –Ɛ<엑스<엑스 0 +Ɛ, 또는 동등하게, │ 엑스– 엑스 0 │<Ɛ. 후자를 실행한다는 것은 점을 치는 것을 의미합니다. 엑스 in Ɛ – 포인트의 이웃 엑스 0 .
예 1:
(2 - 0.1; 2 + 0.1) 또는 (1.9; 2.1) - Ɛ - 이웃.
│엑스– 2│< 0,1
–0,1<엑스 – 2<0,1
2 –0,1<엑스< 2 + 0,1
1,9<엑스< 2,1
예 2:
ㅏ– 제수 세트 24;
비약수 18의 집합입니다.
나는 교육을 받은 이론물리학자이지만 좋은 수학적 배경을 가지고 있습니다. 행정관에서는 과목 중 하나가 철학이었고 주제를 선택하고 그에 대한 논문을 제출해야 했습니다. 대부분의 옵션이 한 번 이상 불쾌했기 때문에 더 이국적인 것을 선택하기로 결정했습니다. 나는 참신한 척하지 않고이 주제에 대해 사용 가능한 모든 / 거의 모든 문헌을 축적했습니다. 철학자와 수학자들은 나에게 돌을 던질 수 있지만 건설적인 비판에만 감사할 것입니다.추신 매우 "건조한 언어"이지만 대학 프로그램 후에는 꽤 읽을 수 있습니다. 대부분의 경우 패러독스의 정의는 Wikipedia에서 가져왔습니다(간단한 표현 및 기성품 TeX 마크업).
소개
집합론 자체와 그 안에 내재된 역설은 그리 오래되지 않은, 불과 100여 년 전에 나타났습니다. 그러나이 기간 동안 먼 길을 여행했으며 어떤 식 으로든 집합 이론은 실제로 대부분의 수학 섹션의 기초가되었습니다. Cantor의 무한과 연결된 역설은 반세기 만에 문자 그대로 성공적으로 설명되었습니다.정의부터 시작해야 합니다.
다중이란 무엇입니까? 질문은 매우 간단하고 그에 대한 대답은 매우 직관적입니다. 집합은 단일 객체로 표현되는 요소 집합입니다. Cantor는 그의 작품 Beiträge zur Begründung der transfiniten Mengenlehre에서 정의를 내립니다. M)을 설정합니다. 보시다시피 본질은 변하지 않고 결정자의 세계관에 의존하는 부분에만 차이가 있습니다. 논리학과 수학 모두에서 집합론의 역사는 매우 논쟁적이다. 사실 Kantor는 19세기에 그 기초를 놓았고, 그 후 Russell과 다른 사람들이 작업을 계속했습니다.
Paradoxes (논리 및 집합 이론) - (그리스어 - 예기치 않은) - 추리의 논리적 정확성을 유지하면서 의미 있는 집합 이론과 형식 논리에서 발생하는 형식적 논리적 모순. 역설은 두 개의 상호 배타적인(모순되는) 명제가 동등하게 증명될 때 발생합니다. 역설은 과학적 이론과 일상적인 추론 모두에서 나타날 수 있습니다(예를 들어, 러셀이 제시한 모든 정상 집합의 집합에 대한 러셀의 역설: "마을 이발사는 면도를 하지 않는 마을 주민을 모두 면도합니다. 스스로 면도?"). 형식적 논리적 모순은 참을 발견하고 증명하는 수단으로서의 추론을 파괴하기 때문에(역설이 나타나는 이론에서는 참이든 거짓이든 모든 문장이 증명 가능하다), 그러한 모순의 근원을 규명하고 발견하는 문제가 생긴다. 그들을 제거하는 방법. 역설에 대한 구체적인 해결책에 대한 철학적 이해의 문제는 형식 논리의 중요한 방법론적 문제 중 하나이며 수학의 논리적 토대입니다.
이 연구의 목적은 고대 이율배반의 상속자로서 집합론의 역설과 새로운 추상화 수준인 무한으로의 전환의 매우 논리적인 결과를 연구하는 것입니다. 임무는 주요 역설, 철학적 해석을 고려하는 것입니다.
집합론의 기본 역설
이발사는 스스로 면도하지 않는 사람만 면도해줍니다. 그는 스스로 면도합니까?
역사에 대한 짧은 여행을 계속합시다.논리적 역설 중 일부는 고대부터 알려져 있었지만 수학적 이론이 산술과 기하학에만 국한되었다는 사실 때문에 집합론과 연관시키는 것은 불가능했습니다. 19세기에 상황은 급격하게 변했습니다. Kantor는 그의 작품에서 새로운 수준의 추상화에 도달했습니다. 그는 무한의 개념을 도입하여 수학의 새로운 분야를 만들었고 "집합의 거듭제곱" 개념을 사용하여 서로 다른 무한을 비교할 수 있게 했습니다. 그러나 그렇게 함으로써 그는 많은 역설을 만들어냈다. 첫 번째는 소위 부랄리-포르티 역설. 수학 문헌에는 서로 다른 용어와 잘 알려진 정리 세트를 기반으로 하는 다양한 공식이 있습니다. 다음은 공식적인 정의 중 하나입니다.
x가 임의의 서수 집합이면 합계 집합은 각 요소보다 크거나 같은 서수임을 증명할 수 있습니다. 엑스. 이제 이것이 모든 서수의 집합이라고 가정합니다. Then은 에 있는 숫자보다 크거나 같은 서수입니다. 그러나 와 는 서수이며, 더욱이 이미 엄격하게 더 크므로 의 어떤 숫자와도 같지 않습니다. 그러나 이것은 모든 서수의 집합이라는 조건과 모순된다.
역설의 본질은 모든 서수의 집합이 형성될 때 모든 서수의 집합이 형성되기 전에 존재했던 "모든"초한 서수에는 아직 없었던 새로운 서수 유형이 형성된다는 것입니다. 이 역설은 Cantor 자신이 발견했으며 이탈리아 수학자 Burali-Forti가 독립적으로 발견하고 출판했으며 후자의 오류는 Russell에 의해 수정되었으며 그 후 공식이 최종 형태를 얻었습니다.
이러한 역설을 피하고 어느 정도 설명하려는 모든 시도 중에서 이미 언급한 러셀의 아이디어가 가장 주목할 만하다. 그는 집합의 요소의 정의가 역설을 일으키는 후자에 의존하는 수학과 논리 함축 문장을 제외할 것을 제안했습니다. 규칙은 다음과 같이 들립니다. "어떤 집합 C도 집합 C에 대해서만 정의된 요소 m과 정의에서 이 집합을 가정할 때 요소 n을 포함할 수 없습니다." . 집합의 정의에 대한 이러한 제한은 역설을 피할 수 있게 해주지만 동시에 수학에서의 적용 범위를 상당히 좁힙니다. 또한 이것만으로는 사상과 언어의 이분법에 뿌리를 둔 그들의 성격과 출현 이유를 형식 논리의 특징으로 설명하기에는 역부족이다. 이 제한은 어느 정도 후기 인지 심리학자와 언어학자가 "기본 수준 분류"라고 부르기 시작한 것과 유사합니다. 정의는 가장 이해하기 쉽고 연구 개념으로 축소됩니다.
모든 집합의 집합이 존재한다고 가정합니다. 이 경우에, 그것은 참입니다. 즉, 모든 집합 t는 V의 부분 집합입니다. 그러나 이것으로부터 어떤 집합의 거듭제곱이 V의 거듭제곱을 초과하지 않는다는 결론이 나옵니다. 부분 집합 V뿐만 아니라 모든 집합에 대해 모든 부분 집합의 집합이 있습니다 , 이전 진술과 모순되는 Cantor의 정리에 의해. 따라서 V는 존재할 수 없으며, 이는 구문적으로 올바른 논리 조건이 집합을 정의한다는 "순진한" 가설, 즉 y를 자유롭게 포함하지 않는 모든 공식 A에 대한 집합을 정의한다는 "순진한" 가설과 충돌합니다. 공리화된 체르멜로-프랭켈 집합론에 근거하여 그러한 모순이 없다는 놀라운 증거가 포터에 의해 제시되었습니다.
논리적인 관점에서 위의 두 역설은 "거짓말쟁이" 또는 "이발사"와 동일합니다. 표현된 판단은 그와 관련된 객관적인 것뿐만 아니라 자신에게도 적용됩니다. 그러나 논리적 측면뿐만 아니라 여기에 존재하는 무한의 개념에도주의를 기울여야합니다. 문헌은 Poincaré의 작업을 참조하며, 그는 다음과 같이 썼습니다.
일반적으로 주요 사항은 다음과 같습니다.
- 이러한 역설에서 술어와 주제의 "영역"을 명확하게 분리하기 위해 규칙을 위반합니다. 혼란의 정도는 한 개념을 다른 개념으로 대체하는 것에 가깝습니다.
- 일반적으로 논리학에서는 추리 과정에서 주어와 술어가 그 양과 내용을 유지한다고 가정합니다. 이 경우
한 범주에서 다른 범주로 전환하여 불일치가 발생합니다. - "all"이라는 단어의 존재는 유한한 수의 요소에 대해 의미가 있지만 무한한 수의 경우 다음과 같은 것을 가질 수 있습니다.
자신을 정의하려면 집합의 정의가 필요합니다. - 기본 논리 법칙이 위반됩니다.
- 주어와 술어의 비동일성이 드러나면 동일성의 법칙을 위반한다.
- 모순의 법칙 - 두 개의 상반된 판단이 동일한 권리로 파생되는 경우;
- 배제된 제3자의 법칙 - 이 제3자가 인정되어야 하고 배제되지 않아야 할 때, 첫 번째도 두 번째도 다른 하나 없이는 인식될 수 없기 때문입니다. 그것들은 동등하게 유효합니다.
자신을 원소로 포함하지 않는 모든 집합의 집합을 K라 하자 K는 자신을 원소로 포함하는가? 그렇다면 K의 정의에 따르면 K의 요소가 아니어야 합니다(모순).그렇지 않으면 K의 정의에 따라 K의 요소여야 합니다. 이 진술은 그들의 관계를 보여주는 Cantor의 역설에서 논리적으로 파생됩니다. 그러나 철학적 본질은 개념의 "자체 이동"이 "우리 눈앞에서"바로 일어나기 때문에 더 분명하게 나타납니다.
Tristram Shandy의 역설:
Stern의 The Life and Opinions of Tristram Shandy, Gentleman에서 주인공은 생애 첫 날의 사건을 이야기하는 데 1년이 걸렸고, 둘째 날을 묘사하는 데 또 1년이 걸렸다는 사실을 알게 됩니다. 이와 관련하여 영웅은 자신의 전기 자료가 처리 할 수있는 것보다 더 빨리 축적되어 결코 완성 할 수 없을 것이라고 불평합니다. 러셀은 “그가 영원히 살았고 그의 일이 그에게 짐이 되지 않는다면, 비록 그의 삶이 처음처럼 다사다난했다 하더라도 그의 전기의 한 부분도 남지 않을 것이라고 주장합니다”라고 러셀은 반대합니다. 씌어 있지 않은.
실제로 Shandy는 n번째 해의 n번째 날의 사건을 설명할 수 있었고, 따라서 그의 자서전에는 매일 매일이 기록되었습니다.
다시 말해, 인생이 무한정 지속된다면 그것은 몇 년 동안 며칠이 될 것입니다.
러셀은 거북이와 함께 이 소설과 제노를 비유합니다. 그의 견해에 따르면 해결책은 전체가 무한대에서 부분과 동일하다는 사실에 있습니다. 저것들. "상식의 공리"만이 모순을 낳습니다. 그러나 문제의 해결책은 순수 수학의 영역에 있습니다. 분명히 일대일 대응이있는 요소 사이에는 연도와 일이라는 두 가지 세트가 있습니다. 그러면 주인공의 무한한 삶이라는 조건 하에 두 개의 무한한 동등한 힘의 집합이 있는데, 집합의 요소 수 개념의 일반화로 힘을 생각하면 역설이 해결됩니다.
Banach-Tarski의 역설(정리) 또는 이중 공 역설- 3차원 공이 2개의 사본으로 동일하게 구성된다는 집합론의 정리.
유클리드 공간의 두 부분집합은 하나가 유한한 수의 부분으로 나누어져 이동되고 두 번째 부분으로 구성될 수 있는 경우 동등 구성이라고 합니다.
보다 정확하게는, 두 집합 A와 B가 각 i에 대해 합동인 서로소 부분 집합의 유한 합집합으로 표현될 수 있는 경우 동일하게 구성됩니다.
선택 정리를 사용하면 정의는 다음과 같이 들립니다.
선택의 공리는 단위 구의 표면이 유한한 수의 부분으로 분할된다는 것을 의미하며, 이러한 구성 요소의 모양을 변경하지 않는 3차원 유클리드 공간의 변환에 의해 두 부분으로 조립될 수 있습니다. 단위 반경의 구체.
분명히, 이러한 부품이 측정 가능해야 한다는 요구 사항을 감안할 때 이 진술은 실현 가능하지 않습니다. 그의 전기에서 유명한 물리학자인 Richard Feynman은 한때 오렌지를 제한된 수의 부분으로 나누고 재구성하는 것에 대한 논쟁에서 어떻게 이겼는지 말했습니다.
특정 지점에서 이 역설은 선택의 공리를 반박하는 데 사용되지만 문제는 우리가 기본 기하학이라고 생각하는 것이 본질적이지 않다는 것입니다. 우리가 직관적이라고 생각하는 개념은 초월 함수의 속성 수준으로 확장되어야 합니다.
선택의 공리가 틀렸다고 믿는 사람들의 신뢰를 더욱 약화시키기 위해 Mazurkiewicz와 Sierpinski의 정리를 언급해야 합니다. 유한한 수의 부분으로 나눌 수 있으므로 등척성으로 집합 E의 덮개로 변환할 수 있습니다.
증명은 선택한 공리의 사용을 요구하지 않습니다.
확실성의 공리를 기반으로 한 추가 구성은 Banach-Tarski 역설에 대한 해결책을 제공하지만 그다지 흥미롭지는 않습니다.
- 리차드의 역설: "이 책에서 명명되지 않은 가장 작은 숫자"를 명명해야 합니다. 모순은 한편으로는 이 책에서 명명된 가장 작은 숫자가 있기 때문에 이것이 행해질 수 있다는 것입니다. 그것으로부터 진행하여 이름이없는 가장 작은 이름을 지정할 수도 있습니다. 그러나 여기서 문제가 발생합니다. 연속체는 셀 수 없습니다. 두 숫자 사이에 무한한 수의 중간 숫자를 삽입할 수 있습니다. 반면에 이 번호에 이름을 붙일 수 있다면 책에 언급되지 않은 클래스에서 언급된 클래스로 자동으로 이동할 것입니다.
- 그렐링-닐슨 패러독스: 단어나 기호는 속성을 나타낼 수 있고 동시에 속성을 가질 수도 있고 갖지 않을 수도 있습니다. 가장 사소한 공식은 다음과 같이 들립니다: "이종론적"("그 자체에 적용할 수 없음"을 의미하는)이라는 단어가 이종론적입니까?.. 그것은 변증법적 모순의 존재로 인해 러셀의 역설과 매우 유사합니다: 형식과 내용의 이중성 위반됩니다. 추상화 수준이 높은 단어의 경우 해당 단어가 이종인지 여부를 판단하는 것은 불가능합니다.
- 스콜렘의 역설: 괴델의 완전성 정리와 뢰벤하임-스콜렘 정리를 사용하여 공리 집합론이 해석을 위해 셀 수 있는 집합 집합만 가정(사용 가능)한 경우에도 참으로 유지됨을 얻습니다. 동시에
공리 이론은 이미 언급한 칸토어의 정리를 포함하며, 이는 셀 수 없는 무한 집합으로 우리를 인도합니다.
역설의 해결
집합론의 생성은 수학의 세 번째 위기로 간주되는 것을 야기했으며, 이는 아직 모두에게 만족스럽게 해결되지 않았습니다.역사적으로 첫 번째 접근 방식은 집합론적이었습니다. 어떤 무한 시퀀스도 무한에서 완성된다고 생각했을 때, 실제 무한대를 사용하는 데 기반을 두었습니다. 아이디어는 집합 이론에서 종종 다른 더 큰 집합의 일부가 될 수 있는 집합에 대해 작업을 수행해야 한다는 것이었습니다. 이 경우 성공적인 조치는 한 가지 경우에만 가능했습니다. 주어진 세트(유한 및 무한)가 완료되었습니다. 반세기 이상 동안 존재했지만 여전히 많은 비판을 불러 일으키는 Nicolas Bourbaki의 전체 수학 학교 인 Zermelo-Fraenkel의 공리 집합 이론입니다.
논리주의는 알려진 모든 수학을 산술의 용어로 환원한 다음 산술의 용어를 수리 논리의 개념으로 환원하려는 시도였습니다. 프레게는 이를 면밀히 따랐지만 작업을 마친 후 러셀이 이론의 모순점을 지적하자 자신의 모순점을 지적하지 않을 수 없었다. 앞에서 언급했듯이 동일한 Russell은 "유형 이론"의 도움으로 함축적 정의의 사용을 제거하려고 시도했습니다. 그러나 그의 집합과 무한대 개념과 환원성 공리는 비논리적인 것으로 판명되었습니다. 주요 문제는 형식 논리와 수학적 논리 사이의 질적 차이가 고려되지 않았으며 직관적인 특성을 포함하여 불필요한 개념이 존재한다는 것입니다.
그 결과 논리학 이론은 무한과 관련된 역설의 변증법적 모순을 제거하지 못했다. 최소한 비 서술 적 정의를 제거 할 수있는 원칙과 방법 만있었습니다. 자신의 추론에서 Russell은 Cantor의 상속인이었습니다.
XIX 말 - XX 세기 초. 수학에 대한 형식 주의적 관점의 확산은 D. Hilbert가 제시 한 공리적 방법 및 수학 입증 프로그램의 개발과 관련이 있습니다. 이 사실의 중요성은 그가 수학계에 제시한 23개의 문제 중 첫 번째 문제가 무한대 문제라는 사실에서 알 수 있습니다. "모든 형이상학을 배제하면서" 고전 수학의 일관성을 증명하기 위해서는 형식화가 필요했습니다. Hilbert가 사용한 수단과 방법을 고려할 때 그의 목표는 근본적으로 불가능한 것으로 판명되었지만 그의 프로그램은 이후의 수학 기초 개발 전체에 큰 영향을 미쳤습니다. Hilbert는 처음으로 기하학의 공리학을 구축하면서 오랫동안 이 문제에 대해 연구했습니다. 문제의 해결이 상당히 성공적이었기 때문에 그는 공리적 방법을 자연수 이론에 적용하기로 결정했습니다. 이와 관련하여 그가 쓴 내용은 다음과 같습니다. 동시에 무한대를 일정한 연산 횟수로 줄임으로써 무한대를 없앨 계획이었다. 이를 위해 그는 무한한 양의 전체 불일치를 보여주기 위해 원자론을 가진 물리학으로 전환했습니다. 사실 힐베르트는 이론과 객관적 실재 사이의 관계에 대한 질문을 제기했다.
유한 방법에 대한 다소 완전한 아이디어는 Hilbert의 학생 J. Herbran이 제공합니다. 유한 추론을 통해 그는 다음 조건을 충족하는 추론을 이해합니다. 논리적 역설 "-항상 유한하고 명확한 수의 객체와 기능만 고려됩니다.
함수에는 정확한 정의가 있으며 이 정의를 통해 값을 계산할 수 있습니다.
그것을 구성하는 방법이 알려지지 않는 한 "이 개체가 존재합니다"라고 주장하지 않습니다.
무한 컬렉션의 모든 개체 X 집합은 고려되지 않습니다.
어떤 추론이나 정리가 이 모든 X에 대해 참이라고 알려져 있다면, 이것은 이 일반적인 추론이 각각의 특정 X에 대해 반복될 수 있음을 의미하며, 이 일반적인 추론 자체는 그러한 특정 추론에 대한 모델로만 간주되어야 합니다.
그러나이 분야의 마지막 출판 당시 Gödel은 이미 그의 결과를 받았으며 본질적으로인지 과정에서 변증법의 존재를 다시 발견하고 승인했습니다. 본질적으로, 수학의 발전은 힐베르트 계획의 실패를 입증했습니다.
괴델은 정확히 무엇을 증명했는가? 세 가지 주요 결과가 있습니다.
1. 괴델은 모든 산술을 포함할 수 있을 만큼 충분히 큰 시스템의 일관성에 대한 수학적 증명이 불가능함을 보여 주었습니다. 이 증명은 시스템 자체에서 발견되는 추론 규칙 이외의 다른 추론 규칙을 사용하지 않을 것입니다. 보다 강력한 추론 규칙을 사용하는 이러한 증명이 유용할 수 있습니다. 그러나 이러한 추론 규칙이 산술 미적분학의 논리적 수단보다 강력하다면 증명에 사용된 가정의 일관성에 대한 확신이 없을 것입니다. 어쨌든 사용된 방법이 유한주의적이지 않으면 Hilbert의 프로그램은 실행 불가능한 것으로 판명될 것입니다. 괴델은 단지 산술의 일관성에 대한 유한주의적 증거를 찾기 위해 계산의 불일치를 보여줄 뿐입니다.
2. 괴델은 공리적 방법의 가능성에 대한 근본적인 한계를 지적했습니다. 산술을 구성하는 다른 시스템과 마찬가지로 수학 원리 시스템은 본질적으로 불완전합니다. 이 시스템의 공리에서 파생되지 않았습니다.
3. 괴델의 정리는 어떤 산술 체계의 확장도 그것을 완전하게 만들 수 없으며, 우리가 그것을 무한한 공리 집합으로 채운다 하더라도 새로운 체계에서는 항상 참이 될 것이지만 이 체계를 통해 추론할 수는 없다는 것을 보여줍니다. 위치. 자연수의 산술에 대한 공리적 접근은 진정한 산술 명제의 전 영역을 포괄할 수 없으며, 우리가 수학적 증명 과정에서 의미하는 바는 공리적 방법의 사용에 국한되지 않습니다. 괴델의 정리 이후로 설득력 있는 수학적 증명의 개념이 단번에 주어질 수 있다고 기대하는 것은 무의미해졌습니다.
집합론을 설명하려는 이 일련의 시도 중 가장 최근에 등장한 것은 직관주의였습니다.
그는 반직관주의, 고유한 직관주의, 초직관주의 등 진화의 여러 단계를 거쳤습니다. 다른 단계에서 수학자들은 다른 문제에 대해 걱정했지만 수학의 주요 문제 중 하나는 무한대 문제입니다. 무한과 연속성의 수학적 개념은 처음부터 철학적 분석의 주제였습니다 (원자론자의 아이디어, Elea의 Zeno의 아포리아, 고대의 극소 방법, 현대의 극소 미적분학 등). 가장 큰 논란은 다양한 유형의 무한대(잠재적, 실제적)를 수학적 대상으로 사용하고 해석하는 데서 발생했습니다. 우리의 의견으로는 이러한 모든 문제는 과학 지식에서 주제의 역할이라는 더 깊은 문제에 의해 생성되었습니다. 사실 수학의 위기상태는 대상(무한)의 세계와 주체의 세계를 비교하는 인식론적 불확실성에 의해 발생한다. 피험자로서의 수학자는 인식의 수단(잠재적 무한대 또는 실제 무한대)을 선택할 가능성이 있습니다. 되기로서의 잠재적 무한의 사용은 그에게 유한한 단계 없이, 구성을 완료하지 않고도, 유한한 것 위에 지을 수 있는 무한한 구성 세트를 구성할 수 있는 기회를 제공합니다. 실제 무한의 사용은 그에게 이미 실현 가능한 무한과 함께 작업할 수 있는 기회를 제공합니다.
반직관주의 단계에서 무한의 문제는 아직 독립된 것이 아니라 수학적 대상을 구성하는 문제와 그것을 정당화하는 방법으로 짜여져 있었다. A. Poincaré의 반 직관주의와 Baire, Lebesgue 및 Borel 함수 이론의 파리 학파 대표자들은 자유 선택 공리의 수용에 반대하여 Zermelo의 정리를 증명했습니다. 모든 세트는 완전히 주문할 수 있지만 필요한 세트의 하위 세트 요소를 결정하는 이론적 방법을 나타내지 않습니다. 수학적 객체를 구성할 방법이 없으며 수학적 객체 자체도 없습니다. 수학자들은 일련의 연구 대상을 구성하는 이론적 방법의 유무가 이 공리를 입증하거나 반박하는 근거가 될 수 있다고 믿었습니다. 러시아어 버전에서 수학의 철학적 기초에 대한 반 직관주의 개념은 N.N.이 개발 한 효과주의와 같은 방향으로 개발되었습니다. 루진. 실효주의는 현실, 선택, 초유한 귀납 등 칸토어의 무한 교리의 주요 추상화에 대한 반대입니다.
실효주의의 경우, 잠재적 타당성의 추상화는 실제 무한성의 추상화보다 인식론적으로 더 가치가 있습니다. 덕분에 함수의 성장이라는 효과적인 개념을 바탕으로 초월한 서수(무한 서수)의 개념을 도입하는 것이 가능해졌습니다. 연속체(continuum)를 나타내기 위한 유효주의의 인식론적 설정은 N.N. Luzin이 만든 불연속적 수단(산술)과 집합(함수)의 기술 이론을 기반으로 합니다. 네덜란드인 L. E. Ya. Brouwer, G. Weyl, A. Heiting의 직관주의는 다양한 유형의 자유롭게 나타나는 시퀀스를 전통적인 연구 대상으로 봅니다. 이 단계에서 모든 수학을 새로운 기반으로 재구성하는 것을 포함하여 적절한 수학적 문제를 해결하면서 직관주의자들은 인지 주체로서 수학자의 역할에 대한 철학적 질문을 제기했습니다. 인식 수단을 선택하는 데 있어 보다 자유롭고 능동적인 그의 입장은 무엇입니까? 직관주의자들은 칸토어의 집합론인 실제 무한의 개념을 비판한 최초의(그리고 반직관주의 단계에서) 건설적인 문제에 대한 해결책을 찾는 과학적 탐색 과정에 영향을 미치는 주체의 능력을 침해하는 것으로 보았다. . 잠재적 무한대를 사용하는 경우 대상은 잠재적 무한대에 대한 아이디어가 실제 무한대에 대한 아이디어보다 직관적으로 훨씬 명확하기 때문에 자신을 속이지 않습니다. 직관주의자에게는 물체가 수학자에게 직접 주어지거나 그것을 구성하는 방법이 알려진 경우 물체가 존재하는 것으로 간주됩니다. 어쨌든 주제는 세트의 여러 요소 구성을 완료하는 과정을 시작할 수 있습니다. 직관주의자에게는 구성되지 않은 물체가 존재하지 않습니다. 동시에 실제 무한대로 작업하는 주체는 이 기회를 박탈당하고 채택된 위치의 이중 취약성을 느낄 것입니다.
1) 이 무한 구성을 수행하는 것은 결코 불가능합니다.
2) 그는 유한한 대상과 같이 실제 무한대로 작동하기로 결정하고, 이 경우 무한 개념의 특수성을 상실합니다. 직관주의는 추상적인 개념의 도움으로 얻어지지만 효과적이고, 설득력 있고, 증명 가능하고, 기능적으로 정확하게 실질적으로 구성되며, 그 자체가 구성으로서 직관적으로 명확한 수단에 의해서만 수학적 대상을 구성할 수 있다는 사실에 의해 수학자의 가능성을 의식적으로 제한합니다. 실제로 그 신뢰성은 의심의 여지가 없습니다. 잠재적 무한의 개념과 건설적인 연구 방법에 의존하는 직관주의는 되기의 수학을 다루고, 집합론은 존재의 수학을 말합니다.
수학적 경험주의의 대표자인 직관주의자 브라우어에게 논리는 부차적이며, 그는 논리와 배제된 중간의 법칙을 비판합니다.
부분적으로 신비로운 그의 작품에서 그는 무한의 존재를 부정하지 않고 현실화를 허용하지 않고 잠재화만을 허용합니다. 그에게 가장 중요한 것은 실제로 사용되는 논리적 수단과 수학적 추론의 해석과 정당화입니다. 직관주의자들이 채택한 제한은 수학에서 무한 개념 사용의 불확실성을 극복하고 수학의 기초에 있는 위기를 극복하려는 열망을 표현합니다.
초 직관주의 (A.N. Kolmogorov, A.A. Markov 및 기타)는 직관주의 개발의 마지막 단계로, 주요 아이디어가 본질을 변경하지 않고 현대화되고 크게 보완되고 변형되지만 단점을 극복하고 긍정적 인 측면을 강화합니다. 기준 수학적 엄격함. 직관주의적 접근법의 약점은 수학적 방법의 정확성과 유효성을 정당화하는 유일한 원천으로서의 직관의 역할에 대한 협소한 이해였습니다. 직관 주의자들은 "직관적 명료성"을 수학의 진리 기준으로 삼아 지식의 주체로서 수학자의 가능성을 방법론적으로 빈곤하게 만들고 그의 활동을 직관에 기반한 정신적 조작으로 만 축소했으며 수학적 지식 과정에 실습을 포함하지 않았습니다. 수학을 입증하는 극도로 직관적인 프로그램은 러시아의 우선 순위입니다. 따라서 국내 수학자들은 직관주의의 한계를 극복하고 인간의 실천을 수학적 개념과 수학적 방법(추론, 구성) 형성의 원천으로 인식하여 유물론적 변증법의 효과적인 방법론을 수용하게 되었다. 수학적 객체의 존재 문제는 정의되지 않은 주관적인 직관 개념이 아니라 수학적 실습과 수학적 객체를 구성하는 특정 메커니즘(계산 가능한 재귀 함수로 표현되는 알고리즘)에 의존하여 초직관주의자에 의해 해결되었습니다.
초직관주의는 모든 방향의 수학자들이 사용하는 건설적인 문제를 해결하기 위한 방법을 주문하고 일반화할 수 있는 가능성으로 구성된 직관주의의 장점을 강화합니다. 따라서 마지막 단계의 직관주의(ultraintuitionism)는 수학에서 구성주의에 가깝다. 인식론적 측면에서 초직관주의의 주요 사상과 원리는 다음과 같다. 추상화를 구성하고 건설적으로 이해하는 방법으로서 식별의 추상화(객체의 다른 속성으로부터의 정신적 추상화 및 객체의 일반 속성의 동시 격리)의 역할에 대한 사용 및 상당한 강화(A.A. Markov의 명시적 지침에 따라) 개념, 수학적 판단; 일관된 이론의 일관성 증명. 형식적 측면에서 식별 추상화의 적용은 반사성, 전이성 및 대칭성의 세 가지 평등 속성(공리)에 의해 정당화됩니다.
A.N. 콜모고로프는 고전논리학과 직관론적 논리, 고전수학과 직관론적 수학의 관계 문제를 해결함으로써 위기의 탈출구를 제시했다. Brouwer의 직관주의는 전체적으로 논리를 거부했지만 어떤 수학자도 논리 없이는 할 수 없기 때문에 논리적 추론의 실천은 여전히 \u200b\u200b직관주의에서 보존되었으며 공리학을 기본으로하는 고전 논리의 일부 원칙이 허용되었습니다. SK Kleene, R. Wesley는 직관 수학이 일종의 미적분학으로 설명될 수 있으며 미적분학은 논리, 형식화 및 그 형식인 알고리즘화를 기반으로 수학적 지식을 구성하는 방법이라고 지적합니다. 특히 부정, A.N. Kolmogorov는 다음과 같이 제안했습니다. 그는 명제와 술어의 공리적 함축적 최소 미적분학의 형태로 직관론적 수학과 밀접하게 관련된 직관론적 논리를 제시했습니다. 그리하여 과학자는 직관만을 인지의 수단으로 인식하는 직관주의의 한계와 수학에서 논리의 가능성을 절대화하는 논리주의의 한계를 극복한 수학적 지식의 새로운 모델을 제시하였다. 이 입장은 유연한 합리성과 그 건설적 효율성의 기초로서 직관적인 것과 논리적인 것의 종합을 수학적 형태로 입증하는 것을 가능하게 했습니다.
결론. 따라서 수학적 지식의 인식론적 측면은 19-20세기로 접어들면서 수학의 기초가 위기에 처한 단계에서의 혁명적 변화를 평가할 수 있게 해준다. 인식 과정, 주제의 본질 및 역할을 이해하는 새로운 위치에서. 전통적인 지식 이론의 인식론적 주체는 수학에서 집합론적 접근이 지배하는 시기에 해당하며, 추상화, 논리, 현실로부터 형식주의, 합리적, 이론적으로 그 대상을 알고 거울로 이해하여 현실을 정확하게 반영하고 복사합니다. 사실 주체는 대상과의 상호작용의 실제 과정이자 결과로서 인식에서 배제되었다. 수학의 철학적 경향 투쟁의 장에 직관주의가 도입되면서 수학자에 대한 새로운 이해가 지식의 주제, 즉 철학적 추상화가 새롭게 구축되어야하는 아는 사람으로 이어졌습니다. 수학자는 경험적 구체성, 가변성, 역사성 등 인식론적 주제에서 추상화된 모든 속성을 포함하여 이미 완전한 실제 사람으로 이해된 경험적 주제로 나타났습니다. 그것은 실제 인식, 창의적이고 직관적이며 창의적인 주제에서 행동하고 인식하는 것입니다. 직관주의 수학의 철학은 인간이 새로운 인지적 자질, 방법, 절차를 소유한 인지의 통합적(전체론적) 주체인 유연한 합리성의 개념에 기반한 현대 인식론적 패러다임의 기초이자 기초가 되었습니다. 추상-인식론적, 논리적-방법론적 본성과 형식을 종합함과 동시에 실존적-인류학적, '역사적-형이상학적' 이해를 수용한다.
중요한 점은 인지, 특히 수학적 개념 형성의 직관입니다. 다시 말하지만, 철학과의 투쟁, 배제된 중간의 법칙을 배제하려는 시도가 있습니다. 수학에서 의미가 없고 철학에서 오는 것입니다. 그러나 직관에 대한 과도한 강조와 명확한 수학적 정당성 부족으로 인해 수학을 견고한 기초로 이전할 수 없었습니다.
그러나 1930년대에 엄격한 알고리즘 개념이 등장한 후 직관주의의 지휘봉은 현대 계산 가능성 이론에 상당한 공헌을 한 수학적 구성주의에 의해 대체되었습니다. 또한 1970년대와 1980년대에는 직관주의자들의 일부 아이디어(이전에는 터무니없게 보였던 아이디어도 포함)와 토포스의 수학적 이론 사이에 중요한 연관성이 발견되었습니다. 일부 topoi에서 발견되는 수학은 직관주의자들이 만들려고 했던 것과 매우 유사합니다.
결과적으로 다음과 같은 진술을 할 수 있습니다. 위의 역설의 대부분은 자기 소유권이 있는 집합 이론에는 단순히 존재하지 않습니다. 그러한 접근 방식이 결정적인지 여부는 논쟁의 여지가 있지만 이 분야에 대한 추가 작업이 표시될 것입니다.
결론
변증법적-유물론적 분석은 역설이 언어와 사고의 이분법, 심오한 변증법(괴델의 정리는 인지 과정에서 변증법을 발현할 수 있게 만들었다)의 표현, 대상과 주체의 개념과 관련된 인식론적 어려움의 결과임을 보여준다. 형식 논리의 영역, 논리 및 집합 이론의 집합(클래스), 과학 등에서 추상 객체를 정의하는 방법을 사용하여 새로운(추상) 객체(무한대)를 도입할 수 있는 추상화 원칙을 사용합니다. 따라서, 모든 역설을 제거하는 보편적인 방법은 주어질 수 없습니다.수학의 세 번째 위기가 끝났는지 여부 (역설과의 인과 관계에 있었기 때문에 이제 역설은 필수적인 부분입니다)-공식적으로 알려진 역설은 1907 년에 제거되었지만 여기에서는 의견이 다릅니다. 그러나 이제 수학에서는 위기 또는 위기를 예고하는 것으로 간주될 수 있는 다른 상황이 있습니다(예: 경로 적분에 대한 엄격한 정당화의 부재).
역설에 관해서는 잘 알려진 거짓말 쟁이 역설이 수학에서 매우 중요한 역할을했으며, 기초의 위기를 초래 한 소위 순진한 (선행 공리) 집합 이론의 일련의 역설 (이러한 역설 중 하나는 H. Frege의 삶에서 치명적인 역할) . 그러나 아마도 역설적이면서도 위기라고 할 수 있는 현대 수학에서 가장 과소평가된 현상 중 하나는 1963년 힐베르트의 첫 번째 문제에 대한 폴 코헨(Paul Cohen)의 해결책일 것입니다. 보다 정확하게는 결정의 사실이 아니라이 결정의 본질입니다.
문학
- 게오르그 칸토어. Beiträge zur begründung der transfiniten mengenlehre. Mathematische Annalen, 46:481-512, 1895.
- 안에. 부로바. 집합론과 변증법의 역설. 과학, 1976.
- MD 도공. 집합론과 그 철학: 비판적 입문서. 옥스포드 대학 출판부, 통합, 2004.
- Zhukov N.I. 수학의 철학적 기초. 민스크: Universitetskoe, 1990.
- Feynman R.F., S. Ilyin. 물론, 당신은 농담하고 있습니다, Mr. Feynman!: 그가 R. Layton에게 말한 놀라운 남자의 모험. 벌새, 2008.
- O. M. Mizhevich. G. Kantor의 집합론에서 역설을 극복하는 두 가지 방법. 논리 및 철학 연구, (3):279--299, 2005.
- S. I. Masalova. 직관주의 수학의 철학. DSTU 게시판, (4), 2006.
- Chechulin V.L. 자체 소유권이 있는 집합 이론(기초 및 일부 응용 프로그램). 파마. 상태 un-t. – 페름, 2012.
- S. N. 트로닌. ""수학 철학"" 분야에 대한 간략한 강의 요약. 카잔, 2012.
- Grishin V.N., Bochvar D.A. 집합론과 비고전적 논리에 관한 연구. 과학, 1976.
- Hofstadter D. Gödel, Escher, Bach: 이 끝없는 화환. Bahrakh-M, 2001.
- Kabakov F.A., Mendelson E. 수학적 논리 소개. 출판사 "Nauka", 1976.
- 예. Bochvar. 수학적 논리와 집합 이론의 역설에 대한 질문. Mathematical Collection, 57(3):369--384, 1944.
I. 집합론의 기본 개념과 공리
수천 년의 존재 기간 동안 수와 도형에 대한 가장 단순한 아이디어에서 수학은 많은 새로운 개념과 방법의 형성에 이르렀습니다. 그것은 자연 연구를 위한 강력한 도구이자 유연한 실천 도구가 되었습니다. 20세기는 수학에 새로운 아이디어와 이론을 도입했고 그 적용 범위가 확대되었습니다. 수학은 과학 체계에서 특별한 위치를 차지합니다. 수학은 인문학이나 자연 과학에 속할 수 없습니다. 그러나 그녀는 그것들에 사용되는 기본 개념을 소개했습니다. 그러한 개념이 수학에서 처음 생겨나 지금은 일반 과학이 된 "집합"의 개념입니다.
집합론의 초안은 Bernard Bolzano(무한의 역설, 1850)에 의해 작성되었습니다. 본 연구에서는 임의의(숫자) 집합을 고려하고 이들의 비교를 위해 일대일 대응의 개념을 정의한다.
19세기 말 독일의 수학자이자 집합론의 창시자인 게오르그 칸토어는 "집합"의 개념을 다음과 같이 직관적으로 정의했습니다. "많은 것은 전체적으로 많은 생각이다". 이러한 집합의 정의에는 도입이 필요했습니다. 세 글자.
첫 번째그들 중 다수는 "하나", 즉 다수를 대표하라. 이러한 기호로 모든 알파벳의 대문자를 사용하는 것이 일반적입니다. 예를 들어 라틴 알파벳 A, B, ..., X 또는 기타 합의의 대문자로 집합을 지정합니다.
두번째기호는 "다"를 나타내야 합니다. 즉, 집합의 요소로 간주되어야 합니다. 이 기호는 같은 알파벳의 소문자를 사용하는 것이 일반적입니다: a, b, ..., z.
제삼기호는 요소를 집합에 명확하게 연결해야 합니다. 기호는 해당 기호로 정의되며 그리스어 단어(to be)의 첫 글자에서 나옵니다. 항목은 관계를 정의합니다. x는 X의 요소입니다. x가 X의 요소가 아님을 나타내려면 를 씁니다.
집합 개념의 이러한 정의는 소위 역설이라는 이론의 여러 내부 모순으로 이어진다는 점에 유의해야 합니다.
예를 들어 러셀의 역설을 생각해 보십시오. 미용사
(요소 x) 자신을 면도하지 않는 어떤 마을에 살고 있는 사람(X는 해당 마을에서 스스로 면도하지 않는 모든 사람의 집합이라고 하자). 이발사는 스스로 면도합니까? 즉, 아니면? 질문에 대답하는 것은 불가능합니다. 예를 들어 , 우리는 즉시 모순에 도달합니다.
학교 수학 과정에서 학생들은 집합의 개념을 정의할 수 없는 개념으로 간주하며, 이는 하나의 전체로 생각되는 우리 주변 현실의 객체 집합으로 이해됩니다. 그리고 이 컬렉션의 각 객체는 이 세트의 요소.
현재 집합 이론의 몇 가지 공리 시스템이 있습니다.
체르멜로의 공리 체계. 이 공리 체계는 종종 선택 공리로 보완되며 선택 공리(ZFC)가 있는 체르멜로-프랭켈 시스템이라고 합니다.
NBG 이론의 공리. von Neumann이 제안한 이 공리 체계는 나중에 Robinson, Bernays 및 Gödel에 의해 수정되고 단순화되었습니다.
체르멜로 시스템(Z-시스템)은 7개의 공리로 구성됩니다. 학교 수학 과정에서 사용되는 틀 내에서 이러한 공리를 설명하겠습니다.
볼륨 공리(Z1).집합 A의 모든 요소가 집합 B에 속하고 집합 B의 모든 요소도 집합 A에 속하면 A=B입니다.
이 공리를 명확히 하기 위해 "부분 집합"이라는 용어를 사용해야 합니다. 집합 A의 각 요소가 집합 Z의 요소이면 A는 부분 집합지, 쓰기 . 기호는 "on"이라고 합니다. Z=A일 가능성이 배제되지 않는다면, 여기에 집중하기 위해 글을 쓴다.
"하위 집합"이라는 용어를 소개하면서 공리 1을 기호 형식으로 공식화합니다. .
쌍공리(Z2).임의의 a와 b에 대해 요소가 (a,b)뿐인 집합이 있습니다.
이 공리는 집합의 데카르트 곱을 설명하는 데 사용되며, 여기서 초기 개념은 "순서가 있는 쌍"입니다. 아래에 순서쌍두 요소의 총체를 이해하고, 각 요소는 기록에서 특정 위치를 차지합니다. 순서쌍은 다음과 같이 표시됩니다: (a, b).
합계 공리(Z3).임의의 세트 A와 B의 경우, 요소가 세트 A의 모든 요소와 세트 B의 모든 요소이고 더 이상 다른 요소를 포함하지 않는 고유한 세트 C가 있습니다.
기호 형식에서 공리 Z3은 다음과 같이 쓸 수 있습니다. . 이 공리와 그에 따른 정리를 기반으로 집합 연산의 속성이 표시되며 이에 대한 설명은 섹션 3에서 제공됩니다. 공리 Z1 및 Z2를 통해 합집합, 교집합, 추가 연산의 개념을 소개할 수 있습니다. , 집합의 차이.
정도의 공리(Z4).모든 집합 X에 대해 모든 부분 집합 P(X)의 집합이 있습니다.
무한의 공리 (Z6).최소한 하나의 무한 집합(자연 수열)이 있습니다.
선택의 공리(Z7). 비어 있지 않은 세트의 모든 패밀리에 대해 이 세트의 요소 중 하나를 패밀리의 각 세트와 연관시키는 기능이 있습니다. 함수가 호출됩니다. 선택 기능주어진 가족을 위해.
해당 공리의 중요성에 주목할 가치가 있습니다. 그 이유는 공리 사이의 집합과 관계가 모든 수학적 분야의 연구 대상이기 때문입니다.
우리는 집합 이론에서 또 다른 중요한 발견인 시각적 표현을 위한 부분 집합 간의 관계 이미지를 지적합니다. 이 방법을 처음 사용한 사람 중 한 사람은 독일의 뛰어난 수학자이자 철학자인 Gottfried Wilhelm Leibniz였습니다. 그런 다음이 방법은 Leonhard Euler에 의해 완전히 개발되었습니다. 오일러 이후 체코의 수학자 베르나르드 볼차노(Bernard Bolzano)가 같은 방법을 개발했습니다. 단, 오일러와 달리 그는 원형이 아니라 직사각형 다이어그램을 그렸습니다. 오일러 원 방법은 독일 수학자 어네스트 슈뢰더도 사용했습니다. 그러나 도식적 방법은 영국의 논리학자 존 벤의 글에서 가장 번성했습니다. 벤을 기리기 위해 오일러 원 대신 해당 수치를 벤 다이어그램이라고 부르며 일부 책에서는 오일러-벤 다이어그램이라고도 합니다. 오일러-벤 다이어그램은 수학과 논리뿐만 아니라 관리 및 기타 응용 분야에서도 사용됩니다.
II. 집합 간의 관계와 집합을 정의하는 방법
따라서 세트는 하나의 전체로 생각할 수 있는 모든 객체의 세트로 이해됩니다. 세트는 성격이 매우 다른 객체로 구성될 수 있습니다. 그 요소는 문자, 원자, 숫자, 방정식, 점, 각도 등이 될 수 있습니다. 이것은 집합론의 극단적인 범위와 가장 다양한 지식 분야(수학, 물리학, 경제학, 언어학 등)에 대한 집합론의 적용을 설명합니다.
세트는 그 요소에 의해 정의된다고 믿어집니다. 즉, 어떤 객체가 이 세트에 속한다고 말할 수 있는지 여부에 따라 세트가 제공됩니다. 집합을 지정하는 방법에는 두 가지가 있습니다.
- 요소 열거.
예를 들어 집합 A가 요소 a, b, c로 구성된 경우 A = (a, b, c)라고 씁니다.
요소 열거를 사용하여 모든 세트를 지정할 수 있는 것은 아닙니다. 모든 요소를 열거할 수 있는 집합을 유한이라고 합니다. 요소를 모두 열거할 수 없는 세트를 무한대라고 합니다. 요소 열거를 사용하여 지정할 수 없습니다. 예외는 이전 요소를 기반으로 각 다음 요소의 형성 순서가 명확한 무한 집합입니다. 예를 들어, 자연수의 집합은 무한 집합입니다. 그러나 두 번째부터 시작하여 각 다음 숫자는 이전 숫자보다 1 더 많은 것으로 알려져 있습니다. 따라서 다음과 같이 N = (1, 2, 3, 4, ...)로 설정할 수 있습니다.
- 집합은 다음을 사용하여 지정할 수 있습니다. 특성 속성 표시.
특성주어진 집합의 는 이 집합의 모든 요소가 가지고 있고 여기에 속하지 않은 요소는 가지고 있지 않은 속성입니다. 이것은 다음과 같이 표시됩니다. A = (x|…), 여기서 수직 막대 뒤에 이 집합 요소의 특성 속성이 기록됩니다.
예를 들어, B=(1,2,3)입니다. 집합 B의 각 요소가 4보다 작은 자연수임을 쉽게 알 수 있습니다. 집합 B의 요소의 이러한 특성이 특징입니다. 이 경우 그들은 다음과 같이 쓰고 읽습니다. "집합 B는 x가 자연수 집합에 속하고 x가 4보다 작은 요소 x로 구성됩니다." 다른 방법으로 지정될 수도 있습니다: 또는 등.
또한 요소가 집합의 특성을 따르지 않으면 이 집합에 속하지 않습니다. 특성 속성(예: )을 지정해야만 지정할 수 있는 집합이 있습니다.
학교 수학 과정에서 특히 중요한 것은 다음과 같습니다. 숫자 세트, 즉. 원소가 숫자인 집합. 수학에서 숫자 집합의 이름에는 특별한 표기법이 허용됩니다.
N = (1, 2, 3, 4, …) - 자연수 집합;
Z = (...,-4, -3, -2, -1, 0, 1, 2, 3, 4, ...) - 정수 집합(모든 자연수와 그 반대를 포함함);
Q = (x | x=p/q, 여기서 p∈Z, q∈N) - 유리수 집합(일반 분수로 나타낼 수 있는 숫자로 구성됨)
J - 비합리적인 숫자의 집합(무한 십진수 비주기적 분수로 구성된 집합, 예: 1,23456342 …; 등)
R = (-∞; +∞) - 실수 집합.
원을 사용하여 묘사된 모든 실수 L. Euler의 집합입니다. (그림 1)

숫자 간격을 사용하여 모든 숫자 집합을 지정할 수 있습니다. (그림 2)
숫자 범위의 유형

위에서 설명한 집합 C는 숫자 집합이며 숫자 간격을 사용하여 지정할 수 있습니다(그림 3).

그림 3 - 숫자 간격
숫자 집합을 지정하는 데 중요한 규칙을 하나 더 지적해 보겠습니다. 유한 숫자 집합은 실제 선에 별도의 점으로 표시됩니다.
수학에서는 때때로 하나의 요소만 포함하는 집합과 단일 요소가 없는 집합을 고려해야 합니다. 어떤 원소도 포함하지 않는 집합을 호출 비어 있는. 기호 ∅로 표시됩니다. 예를 들어 집합 A=(x|x∈N∧-2
둘 이상의 세트에 관해서는 그들 사이에 어떤 관계가 있을 수도 있고 없을 수도 있다는 점은 주목할 가치가 있습니다. 세트가 관계에 있으면 관계에 대해 이야기하고 있습니다. 평등또는 관계 포함.
세트 A 켜다집합 A의 각 요소가 집합 B에 속하는 경우 집합 B로. 이 관계는 다음과 같이 표시됩니다. A⊂B. 또는 다른 방식으로 그들은 집합 A가 집합 B의 부분집합이라고 말합니다.
집합 A와 B를 호출합니다. 동일한, 세트 A의 각 요소가 세트 B에 속하고 동시에 세트 B의 각 요소가 세트 A에 속하는 경우에만. 이 관계는 다음과 같이 표시됩니다. A \u003d B
예를 들어:
1) A=(a,b,c,d) 및 B=(b,d), 이러한 세트는 포함 B⊂A와 관련이 있습니다. 집합 B의 모든 요소는 집합 A에 속합니다.
2) M=(x|x∈R∧x<6}=(-∞;6) и K{x|x∈R∧x≤8}=(-∞;8], эти множества находятся в отношении включения M⊂K, т.к. каждый элемент множества M принадлежит множеству K (Рис. 4)

그림 4 - 숫자 간격
3) A=(x|x∈N∧x:2)=(2,4,6,8,10,...) 및 B=(x|x∈N∧x:3)=(3,6 ,9,12,...), 집합 A에는 집합 B에 속하지 않는 요소 2가 있으므로 이 두 집합은 A⊄B 관계에 있지 않습니다.
및 B⊄A, 왜냐하면 세트 B에는 세트 A에 속하지 않는 요소 3이 있습니다.
따라서 이러한 집합은 어떤 관계도 없습니다.
III. 집합에 대한 연산 및 연산 속성
데프.1. 횡단 세트 A와 B는 연산이며, 그 결과는 동시에 A와 B 모두에 속하는 요소로만 구성된 세트입니다.
A∩B=(x|x∈A∧x∈B)
데프.2.협회세트 A 및 B는 연산이며, 그 결과는 세트 A 또는 세트 B(즉, 이들 세트 중 적어도 하나)에 속하는 요소로만 구성된 세트입니다.
A∪B=(x|x∈A∨x∈B)
데프.3. 차이점세트 A와 B를 연산이라고 하며, 그 결과는 A에 속하고 동시에 B에 속하지 않는 요소로만 구성된 세트입니다.
A\ B =(x∈A∧x∉B)
데프.4. 집합 A를 보편 집합으로 보완집합을 집합이라고 하며 각 요소는 보편에 속하고 A에는 속하지 않습니다.
표현식 설정
세트에서 작업 표시 및 아마도 괄호, 표현식을 형성할 수 있습니다. 예를 들어, A∩B\C.
이러한 식의 작업 순서를 알고 읽을 수 있어야 합니다.
작업 순서
괄호가 없으면 먼저 단순 집합의 범용 집합에 추가한 다음 교집합과 합집합(서로 같음), 마지막으로 차이를 수행합니다.
식에 괄호가 포함되어 있으면 먼저 단락 1)에 지정된 순서대로 괄호 안의 작업을 수행한 다음 괄호 밖의 모든 작업을 수행합니다.
예를 들어, a) A∩B\C; b) A∩(B\C); c) A∩(B\C)" .
식 읽기는 마지막 작업의 결과부터 시작됩니다. 예를 들어 식 a)는 다음과 같이 읽습니다. 두 세트의 차이, 첫 번째는 세트 A와 B의 교집합이고 두 번째는 세트 C입니다.
오일러 서클
집합에 대한 작업과 집합 간의 관계는 오일러 원을 사용하여 나타낼 수 있습니다. 일반 세트는 원으로, 일반 세트는 직사각형으로 표시되는 특수 도면입니다.

일. 오일러 원을 사용하여 세트 (A∪B)"∩C를 그립니다.

해결책. 이 표현식에서 작업 실행 순서를 정렬해 보겠습니다. (A∪B) "∩C. 실행 순서에 따라 작업 결과를 음영 처리합니다.

작업 속성 설정(그림 5)
속성 I - 8 및 1 0 - 8 0은 소위 이중성 원리에 의해 상호 연결됩니다.
속성의 두 열 중 하나에서 기호 ∩→∪, ∪→∩, ∅→U, U→∅가 반전되면 다른 속성 열을 얻을 수 있습니다.

IV. 집합을 클래스로 분할
다음 조건이 충족되면 집합 X가 쌍으로 분리된 하위 집합 또는 클래스로 나누어지는 것으로 간주됩니다.
1) 임의의 두 하위 집합의 교집합이 비어 있습니다.
2) 모든 부분 집합의 합집합은 집합 X와 일치합니다.
집합을 클래스로 나누는 것을 분류라고 합니다.
V. 집합의 데카르트 곱
집합 A와 B의 데카르트 곱은 쌍의 집합이며, 각각의 첫 번째 구성 요소는 집합 A에 속하고 두 번째 구성 요소는 집합 B에 속합니다. 집합 A와 B의 데카르트 곱은 A x B로 표시됩니다. 따라서, A×B=((x,y)|x ∈A˄y∈B). 집합 A와 B의 데카르트 곱을 찾는 작업을 이러한 집합의 데카르트 곱셈이라고 합니다. A와 B가 숫자 집합인 경우 이러한 집합의 데카르트 곱의 요소는 순서가 지정된 숫자 쌍입니다.
VI. 합계 및 제품 규칙
n(A)로 유한 집합 A의 요소 수를 나타냅니다. 집합 A와 B가 교차하지 않으면 n(AUB)= n(A) + n(B)입니다. 집합 A와 B가 교차하면 n(A U B) = n (A) + n (B) - n (A ∩ B)입니다.
세트 A와 B의 데카르트 곱의 요소 수는 n (A X B) = n (A) 공식으로 계산됩니다. 엔(비).
조합론에서 분리된 유한 집합의 합집합의 요소 수를 세는 규칙을 합계 규칙이라고 합니다. 만약 요소 x가 k개의 방법으로 선택될 수 있고 요소 y가 m개의 방법으로 선택될 수 있고, 요소 x가 요소 y를 선택하는 방식과 일치하면 "x 또는 y" 선택은 k + m 방식으로 수행될 수 있습니다.
조합론에서 유한 집합의 데카르트 곱의 요소 수를 계산하는 규칙을 곱 규칙이라고 합니다. 요소 x를 k 방식으로 선택할 수 있고 요소 y를 m 방식으로 선택할 수 있으면 쌍(x, y) km 방식으로 선택할 수 있습니다.
VII. 사용된 소스 목록
Aseev G.G. Abramov O.M., Sitnikov D.E. 이산 수학: 교과서. - Rostov n / a: "Phoenix", Kharkov: "Torsing", 2003, -144s.
Vilenkin N.Ya 대수학. IX를 위한 교과서 - 수학적 전문화가 있는 중등 학교의 X 등급, 1968
Vilenkin N.Ya. 이야기를 설정합니다. M.: 출판사 "Science". - 1965. - 128초
오일러 다이어그램 - Venn.URL: http://studopedia.net/1_5573_diagrammi-eylera-venna.html
Kireenko S.G., Grinshpon I.E. 집합 이론의 요소(교과서). - Tomsk, 2003. - 42p.
Kuratovsky K., Mostovsky A. 집합 이론. - M.: Mir, 1970, - 416s.