La loi de distribution d'une variable aléatoire discrète. Exemples de résolution de problèmes
Définition 3. X a loi de distribution normale (loi gaussienne), si sa densité de distribution est de la forme :
où m = M(X), σ 2=D(X), σ > 0 .
La courbe de distribution normale est appelée courbe normale ou gaussienne(Fig. 6.7).
Une courbe normale est symétrique par rapport à une droite x = m, a un maximum au point x = m, égal.
La fonction de distribution d'une variable aléatoire X, distribuée selon la loi normale, s'exprime en fonction de la fonction de Laplace Ф( X) selon la formule :
F( X) est la fonction de Laplace.
Commenter. Fonction F( X) est impaire (Ф(- X) = -Ф( X)), en outre, lorsque X> 5 peut être considéré comme F( X) ≈ 1/2.
Tableau des valeurs de la fonction Ф( X) est donnée en annexe (tableau P 2.2).
Tracé de la fonction de distribution F(X) est illustré à la Fig. 6.8.
La probabilité qu'une variable aléatoire X prenne des valeurs appartenant à l'intervalle ( un B) sont calculés par la formule :
R(une< X < b ) = .
La probabilité que la valeur absolue de l'écart d'une variable aléatoire par rapport à son espérance mathématique soit inférieure à un nombre positif δ est calculée par la formule :
P(| X -m| .
En particulier, lorsque m=0 l'égalité est vraie :
P(| X | .
"Règle des trois sigma"
Si la variable aléatoire X a une loi de distribution normale avec des paramètres m et σ, alors il est presque certain que ses valeurs sont contenues dans l'intervalle ( m 3σ ; m+ 3σ), puisque P(| X -m| = 0,9973.
Problème 6.3. Valeur aléatoire X distribué normalement avec une moyenne de 32 et une variance de 16. Trouver : a) densité de distribution de probabilité F(X); X prendra une valeur de l'intervalle (28;38).
Solution: Par condition m= 32, σ 2 = 16, donc, σ= 4, alors
une)
b) Utilisons la formule :
R(une< X )= .
Remplacer une= 28, b= 38, m= 32, σ= 4, on obtient
R(28< X < 38)= F(1.5) F(1)
Selon le tableau des valeurs de la fonction Ф( X) on trouve Ф(1.5) = 0.4332, Ф(1) = 0.3413.
La probabilité recherchée est donc :
P(28 Tâches 6.1.
Valeur aléatoire X uniformément réparti dans l'intervalle (-3;5). Trouver: a) densité de distribution F(X);
b) fonctions de répartition F(X);
c) caractéristiques numériques ; d) probabilité R(4<X<6). 6.2.
Valeur aléatoire X uniformément répartis sur le segment. Trouver: a) densité de distribution F(X);
b) fonction de répartition F(X);
c) caractéristiques numériques ; d) probabilité R(3≤X≤6). 6.3.
Un feu de circulation automatique est installé sur l'autoroute, dans lequel le feu vert est allumé pendant 2 minutes, jaune pendant 3 secondes et rouge pendant 30 secondes, etc. Une voiture roule sur l'autoroute à un moment aléatoire. Trouvez la probabilité que la voiture passe le feu sans s'arrêter. 6.4.
Les rames de métro circulent régulièrement à des intervalles de 2 minutes. Le passager entre sur le quai à un moment aléatoire. Quelle est la probabilité que le passager doive attendre plus de 50 secondes pour le train ? Trouver l'espérance mathématique d'une variable aléatoire X- le temps d'attente des trains. 6.5.
Trouvez la variance et l'écart type de la distribution exponentielle donnée par la fonction de distribution : 6.6.
Variable aléatoire continue X donnée par la densité de distribution de probabilité : a) Nommez la loi de distribution de la variable aléatoire considérée. b) Trouver la fonction de distribution F(X) et les caractéristiques numériques de la variable aléatoire X. 6.7.
Valeur aléatoire X distribuée selon la loi exponentielle, donnée par la densité de distribution de probabilité : X prendra une valeur de l'intervalle (2.5;5). 6.8.
Variable aléatoire continue X distribué selon la loi exponentielle donnée par la fonction de distribution : Trouver la probabilité qu'à la suite du test X prendra la valeur de l'intervalle . 6.9.
L'espérance mathématique et l'écart type d'une variable aléatoire normalement distribuée sont respectivement 8 et 2. a) densité distribution f(X); b) la probabilité qu'à la suite du test X prendra une valeur de l'intervalle (10;14). 6.10.
Valeur aléatoire X normalement distribué avec une moyenne de 3,5 et une variance de 0,04. Trouver: a) densité de distribution F(X); b) la probabilité qu'à la suite du test X prendra la valeur de l'intervalle . 6.11.
Valeur aléatoire X distribué normalement avec M(X) =
0 et ré(X)=
1. Lequel des événements : | X|≤0,6 ou | X|≥0,6 a une forte probabilité ? 6.12.
Valeur aléatoire X distribué normalement avec M(X) =
0 et ré(X)=
1. À partir de quel intervalle (-0,5 ; -0,1) ou (1 ; 2) dans un test prendra-t-il une valeur avec une plus grande probabilité ? 6.13.
Le prix actuel par action peut être modélisé en utilisant la distribution normale avec M(X)=
10 jours unités et σ( X) = 0,3 den. unités Trouver: a) la probabilité que le cours actuel de l'action soit de 9,8 den. unités jusqu'à 10,4 deniers. unités; b) en utilisant la "règle de trois sigma" pour trouver les limites dans lesquelles se situera le prix actuel de l'action. 6.14.
La substance est pesée sans erreurs systématiques. Les erreurs de pesée aléatoires sont soumises à la loi normale avec l'écart type σ= 5r. Trouver la probabilité que dans quatre expériences indépendantes l'erreur dans trois pesées ne dépasse pas 3 g en valeur absolue. 6.15.
Valeur aléatoire X distribué normalement avec M(X)= 12.6. La probabilité qu'une variable aléatoire tombe dans l'intervalle (11,4 ; 13,8) est de 0,6826. Trouvez l'écart type σ. 6.16.
Valeur aléatoire X distribué normalement avec M(X) = 12 et ré(X) = 36. Trouvez l'intervalle dans lequel, avec une probabilité de 0,9973, la variable aléatoire tombera à la suite du test X. 6.17.
Une pièce produite par une machine automatique est considérée comme défectueuse si l'écart X son paramètre contrôlé de la valeur nominale dépasse de modulo 2 unités de mesure. On suppose que la variable aléatoire X distribué normalement avec M(X) = 0 et σ( X) = 0,7. Quel pourcentage de pièces défectueuses la machine donne-t-elle ? 3.18.
Paramètre X les pièces sont normalement distribuées avec une espérance mathématique de 2 égale à la valeur nominale et un écart type de 0,014. Trouver la probabilité que l'écart X du modulo de la valeur faciale ne dépassera pas 1 % de la valeur faciale. Réponses v) M(X)=1, ré(X)=16/3, σ( X)= 4/ , d)1/8. v) M(X)=4,5, ré(X) =2 , σ ( X)= , d)3/5. 6.3.
40/51. 6.4.
7/12, M(X)=1. 6.5.
ré(X) = 1/64, σ ( X)=1/8 6.6.
M(X)=1 , ré(X) =2 , σ ( X)= 1 . 6.7.
P(2.5<X<5)=e -1 e -2 ≈0,2325 6.8.
Ð(2≤ X≤5)=0,252. b) R(10 < X < 14) ≈ 0,1574. b) R(3,1 ≤ X ≤ 3,7) ≈ 0,8185. 6.11.
|X|≥0,6. 6.12.
(-0,5; -0,1). 6.13.
a) Ð(9,8 ≤ å ≤ 10,4) ≈ 0,6562 6.14.
0,111. b) (9.1 ; 10.9). 6.15.
σ = 1,2. 6.16.
(-6; 30). 6.17.
0,4 %. - le nombre de garçons parmi 10 nouveau-nés. Il est bien clair que ce nombre n'est pas connu à l'avance, et dans les dix prochains enfants nés, il peut y avoir: Ou les garçons - seul et l'unique des options listées. Et, pour garder la forme, un peu d'éducation physique : - distance de saut en longueur (dans certaines unités). Même le maître du sport n'est pas capable de le prévoir :) Cependant, quelles sont vos hypothèses ? 2) Variable aléatoire continue - prend tout valeurs numériques d'une plage finie ou infinie. Noter
: les abréviations DSV et NSV sont populaires dans la littérature éducative D'abord, analysons une variable aléatoire discrète, puis - continu. - ce conformité entre les valeurs possibles de cette grandeur et leurs probabilités. Le plus souvent, la loi est écrite dans un tableau : Et maintenant point très important: puisque la variable aléatoire nécessairement va accepter une des valeurs, puis la forme des événements correspondants groupe complet et la somme des probabilités de leur occurrence est égale à un : ou, s'il est écrit plié : Ainsi, par exemple, la loi de la distribution des probabilités des points sur un dé a la forme suivante : Sans commentaire. Vous pouvez avoir l'impression qu'une variable aléatoire discrète ne peut prendre que de "bonnes" valeurs entières. Dissipons l'illusion - ils peuvent être n'importe quoi : Exemple 1 Certains jeux ont la loi de distribution des gains suivante : … vous rêvez probablement de telles tâches depuis longtemps :) Laissez-moi vous dire un secret - moi aussi. Surtout après avoir terminé le travail sur théorie des champs. Solution: comme une variable aléatoire ne peut prendre qu'une valeur sur trois, les événements correspondants forment groupe complet, ce qui signifie que la somme de leurs probabilités est égale à un : Nous exposons le "partisan": Contrôle : ce dont vous avez besoin pour vous assurer. Réponse: Il n'est pas rare que la loi de distribution doive être compilée indépendamment. Pour ce faire, utilisez définition classique de la probabilité, théorèmes de multiplication / addition pour les probabilités d'événements et autres jetons tervera: Exemple 2 Il y a 50 billets de loterie dans la boîte, dont 12 gagnants, et 2 d'entre eux gagnent 1000 roubles chacun, et le reste - 100 roubles chacun. Élaborez une loi de distribution d'une variable aléatoire - la taille des gains, si un ticket est tiré au hasard dans la boîte. Solution: comme vous l'avez remarqué, il est d'usage de placer les valeurs d'une variable aléatoire dans ordre croissant. Par conséquent, nous commençons par les plus petits gains, à savoir les roubles. Au total, il y a 50 - 12 = 38 de ces tickets, et selon définition classique: Le reste des cas sont simples. La probabilité de gagner des roubles est de : Vérification : - et c'est un moment particulièrement agréable de telles tâches ! Réponse: la loi de distribution des gains requise : La tâche suivante pour une décision indépendante : Exemple 3 La probabilité que le tireur atteigne la cible est . Faites une loi de distribution pour une variable aléatoire - le nombre de coups après 2 coups. ... Je savais qu'il te manquait :) On s'en souvient théorèmes de multiplication et d'addition. Solution et réponse à la fin de la leçon. La loi de distribution décrit complètement une variable aléatoire, mais en pratique il est utile (et parfois plus utile) de n'en connaître qu'une partie. caractéristiques numériques
. En termes simples, cela valeur moyenne attendue avec des tests répétés. Laisser une variable aléatoire prendre des valeurs avec des probabilités ou sous forme pliée : Calculons, par exemple, l'espérance mathématique d'une variable aléatoire - le nombre de points lâchés sur un dé : Rappelons maintenant notre jeu hypothétique : La question se pose : est-ce même rentable de jouer à ce jeu ? ... qui a des impressions ? Donc, vous ne pouvez pas dire « désinvolte » ! Mais cette question peut être facilement résolue en calculant l'espérance mathématique, essentiellement - moyenne pondérée probabilités de gagner : Ainsi, l'espérance mathématique de ce jeu perdant. Ne vous fiez pas aux impressions - faites confiance aux chiffres ! Oui, ici, vous pouvez gagner 10 ou même 20 à 30 fois de suite, mais à long terme, nous serons inévitablement ruinés. Et je ne vous conseillerais pas de jouer à de tels jeux :) Eh bien, peut-être seulement pour s'amuser. De tout ce qui précède, il s'ensuit que l'espérance mathématique n'est PAS une valeur ALÉATOIRE. Tâche créative pour la recherche indépendante : Exemple 4 Monsieur X joue à la roulette européenne selon le système suivant : il mise constamment 100 roubles sur le rouge. Composez la loi de distribution d'une variable aléatoire - son gain. Calculez l'espérance mathématique des gains et arrondissez-la à kopecks. combien moyenne le joueur perd-il pour chaque pari de cent ? référence
: La roulette européenne contient 18 secteurs rouges, 18 noirs et 1 vert ("zéro"). En cas de chute "rouge", le joueur est payé un pari double, sinon il va au revenu du casino Il existe de nombreux autres systèmes de roulette pour lesquels vous pouvez créer vos propres tables de probabilités. Mais c'est le cas lorsque nous n'avons pas besoin de lois et de tables de distribution, car il est établi avec certitude que l'espérance mathématique du joueur sera exactement la même. Seuls les changements d'un système à l'autre 1.2.4. Variables aléatoires et leurs distributions Distributions de variables aléatoires et fonctions de distribution. La distribution d'une variable aléatoire numérique est une fonction qui détermine de manière unique la probabilité qu'une variable aléatoire prenne une valeur donnée ou appartienne à un intervalle donné. La première est si la variable aléatoire prend un nombre fini de valeurs. Alors la distribution est donnée par la fonction P(X = x), donnant chaque valeur possible X Variable aléatoire X la probabilité que X = x. La seconde est si la variable aléatoire prend une infinité de valeurs. Ceci n'est possible que lorsque l'espace de probabilité sur lequel la variable aléatoire est définie est constitué d'un nombre infini d'événements élémentaires. Alors la distribution est donnée par l'ensemble des probabilités Pennsylvanie <
X Pennsylvanie <
X Cette relation montre que, tout comme la distribution peut être calculée à partir de la fonction de distribution, inversement, la fonction de distribution peut être calculée à partir de la distribution. Les fonctions de distribution utilisées dans les méthodes de prise de décision probabiliste-statistique et dans d'autres recherches appliquées sont soit discrètes, soit continues, ou des combinaisons de celles-ci. Les fonctions de distribution discrètes correspondent à des variables aléatoires discrètes qui prennent un nombre fini de valeurs ou de valeurs d'un ensemble dont les éléments peuvent être renumérotés par des nombres naturels (de tels ensembles sont appelés dénombrables en mathématiques). Leur graphique ressemble à un escabeau (Fig. 1). Exemple 1 Nombre X d'articles défectueux du lot prend la valeur 0 avec une probabilité de 0,3, la valeur 1 avec une probabilité de 0,4, la valeur 2 avec une probabilité de 0,2 et la valeur 3 avec une probabilité de 0,1. Graphique de la fonction de distribution d'une variable aléatoire X illustré à la Fig.1. Fig. 1. Graphique de la fonction de distribution du nombre de produits défectueux. Les fonctions de distribution continue n'ont pas de sauts. Ils augmentent de manière monotone à mesure que l'argument augmente, de 0 pour à 1 pour . Les variables aléatoires avec des fonctions de distribution continues sont dites continues. Les fonctions de distribution continue utilisées dans les méthodes de prise de décision probabiliste-statistique ont des dérivées. Dérivée première f(x) fonctions de répartition F (x) s'appelle la densité de probabilité, La fonction de distribution peut être déterminée à partir de la densité de probabilité : Pour toute fonction de distribution Les propriétés énumérées des fonctions de distribution sont constamment utilisées dans les méthodes de prise de décision probabiliste-statistique. En particulier, la dernière égalité implique une forme spécifique des constantes dans les formules des densités de probabilité considérées ci-dessous. Exemple 2 La fonction de distribution suivante est souvent utilisée : où une et b- quelques chiffres une . Trouvons la densité de probabilité de cette fonction de distribution : (aux points X = un et x = b fonction dérivée F (x) n'existe pas). Une variable aléatoire de fonction de distribution (1) est dite "uniformément distribuée sur l'intervalle [ une; b]». Les fonctions de distribution mixtes se produisent, en particulier, lorsque les observations s'arrêtent à un moment donné. Par exemple, lors de l'analyse de données statistiques obtenues à l'aide de plans de test de fiabilité qui prévoient la fin des tests après une certaine période de temps. Ou lors de l'analyse de données sur des produits techniques nécessitant des réparations sous garantie. Exemple 3 Soit, par exemple, la durée de vie d'une ampoule électrique une variable aléatoire avec une fonction de distribution F(t), et l'essai est effectué jusqu'à ce que l'ampoule tombe en panne, si cela se produit moins de 100 heures après le début de l'essai, ou jusqu'au moment t0= 100 heures. Laisser G(t)- fonction de distribution du temps de fonctionnement de la lampe en bon état dans cet essai. Puis Une fonction G(t) a un saut à un point t0, puisque la variable aléatoire correspondante prend la valeur t0 avec probabilité 1- F(t0)> 0.
Caractéristiques des variables aléatoires. Dans les méthodes de prise de décision probabiliste-statistique, un certain nombre de caractéristiques de variables aléatoires sont utilisées, exprimées par des fonctions de distribution et une densité de probabilité. Lors de la description de la différenciation des revenus, lors de la recherche de limites de confiance pour les paramètres de distributions de variables aléatoires, et dans de nombreux autres cas, un concept tel que «quantile d'ordre» est utilisé. R", où 0< p < 1 (обозначается x p). Quantile de commande R est la valeur d'une variable aléatoire dont la fonction de distribution prend la valeur R ou il y a un "saut" à partir d'une valeur inférieure à R jusqu'à une valeur supérieure R(fig. 2). Il peut arriver que cette condition soit satisfaite pour toutes les valeurs de x appartenant à cet intervalle (c'est-à-dire que la fonction de répartition est constante sur cet intervalle et vaut R). Alors chacune de ces valeurs est appelée un "quantile de l'ordre R". Pour les fonctions de distribution continues, en règle générale, il existe un seul quantile x p ordre R(Fig. 2), et F(x p) = p. (2) Fig.2. Définition d'un quantile x p ordre R. Exemple 4 Trouvons le quantile x p ordre R pour la fonction de distribution F (x)À partir de 1). À 0< p <
1 квантиль x p se trouve à partir de l'équation celles. x p
= a + p(b – a) = a( 1- p)+pb. À p= 0 quelconque X <
une est le quantile d'ordre p= 0. Quantile de commande p= 1 est n'importe quel nombre X >
b. Pour les distributions discrètes, en règle générale, il n'y a pas x p satisfaisant l'équation (2). Plus précisément, si la distribution d'une variable aléatoire est donnée dans le tableau 1, où x1< x 2 < … < x k
, puis l'égalité (2), considérée comme une équation par rapport à x p, n'a de solutions que pour k valeurs p, à savoir, p \u003d p 1, p \u003d p 1 + p 2, p \u003d p 1 + p 2 + p 3, p \u003d p 1 + p 2 + ...+
pm, 3 <
m <
k,
p =
p 1
+
p 2
+ … +
paquet.
Tableau 1. Distribution d'une variable aléatoire discrète Pour la liste k valeurs de probabilité p Solution x p l'équation (2) n'est pas unique, à savoir, F (x) = p 1 + p 2 + ... + p m pour tous X tel que x m< x <
xm+1 . Celles. xp- n'importe quel nombre de la plage (x m ; x m+1 ]. Pour tout le monde Rà partir de l'intervalle (0;1) non inclus dans la liste (3), il y a un "saut" d'une valeur inférieure à R jusqu'à une valeur supérieure R. A savoir, si p 1 + p 2 + … + p m ensuite x p \u003d x m + 1. La propriété considérée des distributions discrètes crée des difficultés importantes dans la tabulation et l'utilisation de ces distributions, car il est impossible de maintenir avec précision les valeurs numériques typiques des caractéristiques de distribution. C'est notamment le cas pour les valeurs critiques et les niveaux de signification des tests statistiques non paramétriques (voir ci-dessous), puisque les distributions des statistiques de ces tests sont discrètes. Le quantile d'ordre est d'une grande importance en statistique. R= ½. On l'appelle la médiane (variable aléatoire X ou sa fonction de distribution F(x)) et noté Moi(X). En géométrie, il existe le concept de "médiane" - une ligne droite passant par le sommet d'un triangle et divisant son côté opposé en deux. En statistique mathématique, la médiane ne coupe pas en deux le côté du triangle, mais la distribution d'une variable aléatoire : l'égalité F(x0.5)= 0,5 signifie que la probabilité d'aller à gauche x0.5 et la probabilité de réussir x0.5(ou directement à x0.5) sont égaux entre eux et égaux à ½, c'est-à-dire P(X < X 0,5) = P(X >
X 0,5) = ½. La médiane indique le "centre" de la distribution. Du point de vue de l'un des concepts modernes - la théorie des procédures statistiques stables - la médiane est une meilleure caractéristique d'une variable aléatoire que l'espérance mathématique. Lors du traitement des résultats de mesure dans une échelle ordinale (voir le chapitre sur la théorie de la mesure), la médiane peut être utilisée, mais pas l'espérance mathématique. Une telle caractéristique d'une variable aléatoire en tant que mode a une signification claire - la valeur (ou les valeurs) d'une variable aléatoire correspondant à un maximum local de la densité de probabilité pour une variable aléatoire continue ou à un maximum local de la probabilité pour une variable aléatoire discrète variable. Si x0 est le mode d'une variable aléatoire de densité f (x), puis, comme le sait le calcul différentiel, . Une variable aléatoire peut avoir plusieurs modes. Ainsi, pour une distribution uniforme (1) chaque point X tel que une< x < b
, c'est la mode. Cependant, ceci est une exception. La plupart des variables aléatoires utilisées dans les méthodes de prise de décision probabilistes-statistiques et d'autres recherches appliquées ont un mode. Les variables aléatoires, les densités, les distributions qui ont un mode sont appelées unimodales. L'espérance mathématique pour les variables aléatoires discrètes avec un nombre fini de valeurs est considérée dans le chapitre "Evénements et probabilités". Pour une variable aléatoire continue X valeur attendue M(X) satisfait l'égalité qui est un analogue de la formule (5) de l'énoncé 2 du chapitre "Evénements et probabilités". Exemple 5 Espérance mathématique pour une variable aléatoire uniformément distribuée Xéquivaut à Pour les variables aléatoires considérées dans ce chapitre, toutes les propriétés des espérances mathématiques et des variances qui ont été considérées précédemment pour les variables aléatoires discrètes avec un nombre fini de valeurs sont vraies. Cependant, nous ne fournissons pas de preuves de ces propriétés, car elles nécessitent un approfondissement des subtilités mathématiques, ce qui n'est pas nécessaire pour la compréhension et l'application qualifiée des méthodes d'aide à la décision probabiliste-statistique. Commenter. Dans ce manuel, les subtilités mathématiques sont délibérément évitées, liées notamment aux notions d'ensembles mesurables et de fonctions mesurables, à l'algèbre des événements, etc. Ceux qui souhaitent maîtriser ces concepts doivent se référer à la littérature spécialisée, en particulier à l'encyclopédie. Chacune des trois caractéristiques - espérance mathématique, médiane, mode - décrit le "centre" de la distribution de probabilité. Le concept de "centre" peut être défini de différentes manières - d'où les trois caractéristiques différentes. Cependant, pour une classe importante de distributions - unimodale symétrique - les trois caractéristiques coïncident. Densité de distribution f(x) est la densité de la distribution symétrique, s'il existe un nombre x 0 tel que L'égalité (3) signifie que le graphe de la fonction y = f(x) symétrique par rapport à une verticale passant par le centre de symétrie X = X 0 . De (3) il s'ensuit que la fonction de distribution symétrique satisfait la relation Pour une distribution symétrique avec un mode, la moyenne, la médiane et le mode sont identiques et égaux x 0. Le cas le plus important est la symétrie par rapport à 0, c'est-à-dire x 0= 0. Alors (3) et (4) deviennent des égalités respectivement. Les relations ci-dessus montrent qu'il n'est pas nécessaire de tabuler des distributions symétriques pour tous X, il suffit d'avoir des tables pour X >
x0. Nous notons une autre propriété des distributions symétriques, qui est constamment utilisée dans les méthodes de prise de décision probabiliste-statistique et dans d'autres recherches appliquées. Pour une fonction de distribution continue P(|X| <
a) = P(-a <
X <
a) = F(a) – F(-a), où F est la fonction de distribution de la variable aléatoire X. Si la fonction de distribution F est symétrique par rapport à 0, c'est-à-dire la formule (6) est valable pour lui, alors P(|X| <
a) = 2F(a) – 1.
Une autre formulation de l'énoncé considéré est souvent utilisée : si Si et sont des quantiles d'ordre et, respectivement (voir (2)) d'une fonction de répartition symétrique par rapport à 0, alors il résulte de (6) que A partir des caractéristiques de la position - l'espérance mathématique, la médiane, le mode - passons aux caractéristiques de la propagation d'une variable aléatoire X: variance , écart type et coefficient de variation v. La définition et les propriétés de la variance pour les variables aléatoires discrètes ont été examinées dans le chapitre précédent. Pour les variables aléatoires continues L'écart type est la valeur non négative de la racine carrée de la variance : Le coefficient de variation est le rapport de l'écart type à l'espérance mathématique : Le coefficient de variation est appliqué lorsque M(X)> 0. Il mesure la propagation en unités relatives, tandis que l'écart type est en unités absolues. Exemple 6 Pour une variable aléatoire uniformément distribuée X trouver la variance, l'écart-type et le coefficient de variation. La dispersion est : La substitution de variable permet d'écrire : où c = (b –
une)/
2. Par conséquent, l'écart type est égal à et le coefficient de variation est : Pour chaque variable aléatoire X déterminer trois autres quantités - centrées Oui, normalisé V et donné tu. Variable aléatoire centrée Oui est la différence entre la variable aléatoire donnée X et son espérance mathématique M(X), celles. Oui = X - M(X). Espérance mathématique d'une variable aléatoire centrée Oui est égal à 0, et la variance est la variance de la variable aléatoire donnée : M(Oui)
= 0, ré(Oui) =
ré(X).
fonction de répartition F Y(X)
variable aléatoire centrée Oui lié à la fonction de distribution F(X)
variable aléatoire initiale X rapport: F Y(X) =
F(X +
M(X)).
Pour les densités de ces variables aléatoires, l'égalité fY(X) =
F(X +
M(X)).
Variable aléatoire normalisée V est le rapport de cette variable aléatoire Xà son écart-type, c'est-à-dire . Espérance mathématique et variance d'une variable aléatoire normalisée V exprimé par des caractéristiques X Alors: où v est le coefficient de variation de la variable aléatoire d'origine X. Pour la fonction de distribution FV(X)
et densité fV(X)
variable aléatoire normalisée V on a: où F(X)
est la fonction de distribution de la variable aléatoire d'origine X, une F(X)
est sa densité de probabilité. Variable aléatoire réduite tu est une variable aléatoire centrée et normalisée : Pour une variable aléatoire réduite Les variables aléatoires normalisées, centrées et réduites sont constamment utilisées tant dans la recherche théorique que dans les algorithmes, les produits logiciels, la documentation réglementaire et technique et pédagogique et méthodologique. En particulier, parce que les égalités Des transformations de variables aléatoires et de plan plus général sont utilisées. Donc si Oui = hache + b, où une et b sont des nombres, alors Exemple 7 Si donc Oui est la variable aléatoire réduite, et les formules (8) sont transformées en formules (7). Avec chaque variable aléatoire X vous pouvez connecter beaucoup de variables aléatoires Oui donnée par la formule Oui = hache + bà divers une>
0 et b.
Cet ensemble est appelé famille à changement d'échelle, généré par une variable aléatoire X. Fonctions de répartition F Y(X)
constituent une famille de distributions à décalage d'échelle générée par la fonction de distribution F(X).
À la place de Oui = hache + b notation fréquemment utilisée Nombre Avec est appelé le paramètre de décalage, et le nombre ré- paramètre d'échelle. La formule (9) montre que X- le résultat de la mesure d'une certaine quantité - entre dans À- le résultat de la mesure de la même valeur, si le début de la mesure est déplacé au point Avec, puis utilisez la nouvelle unité de mesure, dans ré fois supérieur à l'ancien. Pour la famille à décalage d'échelle (9), la distribution X est dite standard. Dans les méthodes de prise de décision probabiliste-statistique et d'autres recherches appliquées, la distribution normale standard, la distribution standard de Weibull-Gnedenko, la distribution gamma standard, etc. sont utilisées (voir ci-dessous). D'autres transformations de variables aléatoires sont également utilisées. Par exemple, pour une variable aléatoire positive X envisagent Oui= journal X, où lg X est le logarithme décimal du nombre X. Chaîne d'égalités F Y (x) = P( lg X< x) = P(X
< 10x) = F( 10X) relie les fonctions de distribution X et Oui. Lors du traitement des données, de telles caractéristiques d'une variable aléatoire sont utilisées X comme des moments d'ordre q, c'est à dire. attentes mathématiques d'une variable aléatoire Xq, q= 1, 2, … Ainsi, l'espérance mathématique elle-même est un moment d'ordre 1. Pour une variable aléatoire discrète, le moment d'ordre q peut être calculé comme Pour une variable aléatoire continue Moments de commande q aussi appelé les instants initiaux de l'ordre q,
contrairement aux caractéristiques connexes - les moments centraux de l'ordre q,
donnée par la formule Ainsi, la dispersion est un moment central d'ordre 2. Distribution normale et théorème central limite. Dans les méthodes décisionnelles probabilistes-statistiques, on parle souvent de distribution normale. Parfois, ils essaient de l'utiliser pour modéliser la distribution des données initiales (ces tentatives ne sont pas toujours justifiées - voir ci-dessous). Plus important encore, de nombreuses méthodes de traitement des données reposent sur le fait que les valeurs calculées ont des distributions proches de la normale. Laisser X 1
,
X 2
,…,
X n M(X je) =
m et dispersions ré(X je)
= , je
= 1, 2,…, n,… Comme il ressort des résultats du chapitre précédent, Considérons la variable aléatoire réduite U n pour la somme Comme il ressort des formules (7), M(U n)
= 0, ré(U n)
= 1. (pour des termes identiquement distribués). Laisser X 1
,
X 2
,…,
X n, … sont des variables aléatoires indépendantes distribuées de manière identique avec des attentes mathématiques M(X je) =
m et dispersions ré(X je)
= , je
= 1, 2,…, n,… Alors pour tout x il y a une limite où F(x) est la fonction de distribution normale standard. En savoir plus sur la fonction F(x) - ci-dessous (il lit "fi de x", parce que F- lettre majuscule grecque "phi"). Le théorème central limite (CLT) tire son nom du fait qu'il s'agit du résultat mathématique central le plus fréquemment utilisé de la théorie des probabilités et des statistiques mathématiques. L'histoire du CLT dure environ 200 ans - de 1730, lorsque le mathématicien anglais A. De Moivre (1667-1754) publia le premier résultat lié au CLT (voir ci-dessous à propos du théorème de Moivre-Laplace), jusqu'aux années vingt - trente du XXe siècle, lorsque Finn J.W. Lindeberg, le français Paul Levy (1886-1971), le yougoslave V. Feller (1906-1970), le russe A.Ya. Khinchin (1894-1959) et d'autres scientifiques ont obtenu les conditions nécessaires et suffisantes pour la validité du théorème central limite classique. Le développement du sujet considéré ne s'est pas du tout arrêté là - ils ont étudié des variables aléatoires qui n'ont pas de dispersion, c'est-à-dire ceux pour qui (académicien B.V. Gnedenko et autres), la situation où des variables aléatoires (plus précisément, des éléments aléatoires) de nature plus complexe que les nombres sont additionnées (universitaires Yu.V. Prokhorov, A.A. Borovkov et leurs associés), etc. .d. fonction de répartition F(x) est donnée par l'égalité où est la densité de la distribution normale standard, qui a une expression assez compliquée : Ici \u003d 3,1415925 ... est un nombre connu en géométrie, égal au rapport de la circonférence au diamètre, e
\u003d 2,718281828 ... - la base des logarithmes naturels (pour retenir ce nombre, notez que 1828 est l'année de naissance de l'écrivain Léon Tolstoï). Comme le sait l'analyse mathématique, Lors du traitement des résultats des observations, la fonction de distribution normale n'est pas calculée selon les formules ci-dessus, mais est trouvée à l'aide de tableaux spéciaux ou de programmes informatiques. Les meilleurs «tableaux de statistiques mathématiques» russes ont été compilés par les membres correspondants de l'Académie des sciences de l'URSS L.N. Bolchev et N.V. Smirnov. La forme de la densité de la distribution normale standard découle de la théorie mathématique, que nous ne pouvons pas considérer ici, ainsi que de la preuve du CLT. A titre d'illustration, nous présentons des petits tableaux de la fonction de distribution F(x)(tableau 2) et ses quantiles (tableau 3). Une fonction F(x) est symétrique par rapport à 0, ce qui est reflété dans les tableaux 2-3. Tableau 2. Fonction de la distribution normale standard. Si la variable aléatoire X a une fonction de distribution F(x), ensuite M(X) = 0, ré(X)
= 1. Cette affirmation est prouvée dans la théorie des probabilités basée sur la forme de la densité de probabilité . Il est d'accord avec une déclaration similaire pour les caractéristiques de la variable aléatoire réduite U n, ce qui est tout à fait naturel, puisque la CLT stipule qu'avec une augmentation infinie du nombre de termes, la fonction de distribution U n tend vers la fonction de distribution normale standard F(x), et pour tout X. Tableau 3 Quantiles de la distribution normale standard. Quantile de commande R Quantile de commande R Introduisons le concept de famille de distributions normales. Par définition, une distribution normale est la distribution d'une variable aléatoire X, pour laquelle la distribution de la variable aléatoire réduite est F(x). Comme il ressort des propriétés générales des familles de distributions à décalage d'échelle (voir ci-dessus), la distribution normale est la distribution d'une variable aléatoire où X est une variable aléatoire de distribution F(X), de plus m =
M(Oui),
= ré(Oui).
Distribution normale avec paramètres de décalage m et l'échelle est généralement notée N(m, )
(parfois la notation N(m, )
). Comme il ressort de (8), la densité de probabilité de la distribution normale N(m, )
il y a Les distributions normales forment une famille à décalage d'échelle. Dans ce cas, le paramètre d'échelle est ré= 1/ , et le paramètre de décalage c = -
m/ . Pour les moments centraux du troisième et du quatrième ordre de la distribution normale, les égalités sont vraies Ces égalités sous-tendent les méthodes classiques de vérification que les résultats des observations suivent une distribution normale. À l'heure actuelle, il est généralement recommandé de vérifier la normalité par le critère O Shapiro - Wilka. Le problème de contrôle de normalité est discuté ci-dessous. Si variables aléatoires X 1 et X2 ont des fonctions de distribution N(m 1
, 1)
et N(m 2
, 2)
respectivement, alors X 1+ X2 a une répartition a une répartition N(m, )
. Ces propriétés de la distribution normale sont constamment utilisées dans diverses méthodes de prise de décision probabiliste-statistique, en particulier dans le contrôle statistique des processus technologiques et dans le contrôle d'acceptation statistique par un attribut quantitatif. La distribution normale définit trois distributions qui sont maintenant couramment utilisées dans le traitement statistique des données. Distribution (chi - carré) - distribution d'une variable aléatoire où les variables aléatoires X 1
,
X 2
,…,
X n sont indépendants et ont la même distribution N(0,1). Dans ce cas, le nombre de termes, c'est-à-dire n, est appelé le "nombre de degrés de liberté" de la distribution du chi carré. Distribution t Student est la distribution d'une variable aléatoire où les variables aléatoires tu et X indépendant, tu a une distribution normale standard N(0,1) et X– chi de distribution – carré avec
n degrés de liberté. Où n est appelé le "nombre de degrés de liberté" de la distribution de Student. Cette distribution a été introduite en 1908 par le statisticien anglais W. Gosset, qui travaillait dans une fabrique de bière. Des méthodes probabilistes-statistiques ont été utilisées pour prendre des décisions économiques et techniques dans cette usine, de sorte que sa direction a interdit à V. Gosset de publier des articles scientifiques sous son propre nom. De cette manière, un secret commercial était protégé, le "savoir-faire" sous la forme de méthodes probabilistes-statistiques développées par W. Gosset. Cependant, il a pu publier sous le pseudonyme "Student". L'histoire de Gosset - Student montre que pendant encore cent ans la grande efficacité économique des méthodes de décision probabilistes-statistiques était évidente pour les managers britanniques. La distribution de Fisher est la distribution d'une variable aléatoire où les variables aléatoires X 1 et X2 sont indépendants et ont des distributions de chi - le carré avec le nombre de degrés de liberté k 1
et k 2
respectivement. Au même moment, un couple (k 1
,
k 2
)
est une paire de "nombres de degrés de liberté" de la distribution de Fisher, à savoir, k 1
est le nombre de degrés de liberté du numérateur, et k 2
est le nombre de degrés de liberté du dénominateur. La distribution de la variable aléatoire F porte le nom du grand statisticien anglais R. Fisher (1890-1962), qui l'utilisa activement dans ses travaux. Des expressions pour les fonctions de distribution de chi - carré, Student et Fisher, leurs densités et caractéristiques, ainsi que des tableaux peuvent être trouvés dans la littérature spécialisée (voir, par exemple,). Comme déjà noté, les distributions normales sont actuellement souvent utilisées dans les modèles probabilistes dans divers domaines appliqués. Pourquoi cette famille de distributions à deux paramètres est-elle si répandue ? Elle est explicitée par le théorème suivant. Théorème central limite(pour des termes distribués différemment). Laisser X 1
,
X 2
,…,
X n,… sont des variables aléatoires indépendantes avec des attentes mathématiques M(X 1
), M(X 2
),…, M(X n), … et les dispersions ré(X 1
),
ré(X 2
),…,
ré(X n), … respectivement. Laisser Ensuite, sous la validité de certaines conditions qui assurent la modicité de la contribution de l'un des termes à U n, pour tout le monde X. Les conditions en question ne seront pas formulées ici. Ils peuvent être trouvés dans la littérature spécialisée (voir, par exemple,). "Clarifier les conditions dans lesquelles le CPT fonctionne est le mérite des éminents scientifiques russes A.A. Markov (1857-1922) et, en particulier, A.M. Lyapunov (1857-1918)". Le théorème central limite montre que dans le cas où le résultat de la mesure (observation) est formé sous l'influence de nombreuses raisons, chacune d'elles n'apportant qu'une petite contribution, et le résultat cumulé est déterminé par additivement, c'est à dire. par addition, alors la distribution du résultat de la mesure (observation) est proche de la normale. On pense parfois que pour que la distribution soit normale, il suffit que le résultat de la mesure (observation) X formé sous l'influence de nombreuses causes, dont chacune a un petit effet. Ce n'est pas vrai. Ce qui compte, c'est comment ces causes agissent. Si additif, alors X a une distribution approximativement normale. Si multiplicativement(c'est-à-dire que les actions des causes individuelles sont multipliées et non ajoutées), alors la distribution X pas proche de la normale, mais de la soi-disant. logarithmiquement normal, c'est-à-dire ne pas X, et lg X a une distribution approximativement normale. S'il n'y a aucune raison de croire que l'un de ces deux mécanismes de formation du résultat final (ou un autre mécanisme bien défini) fonctionne, alors à propos de la distribution X rien de précis ne peut être dit. De ce qui a été dit, il s'ensuit que dans un problème appliqué spécifique, la normalité des résultats des mesures (observations), en règle générale, ne peut pas être établie à partir de considérations générales, elle doit être vérifiée à l'aide de critères statistiques. Ou utiliser des méthodes statistiques non paramétriques qui ne reposent pas sur des hypothèses sur les fonctions de distribution des résultats de mesure (observations) appartenant à l'une ou l'autre famille paramétrique. Distributions continues utilisées dans les méthodes de prise de décision probabilistes-statistiques. En plus de la famille des distributions normales à décalage d'échelle, un certain nombre d'autres familles de distribution sont largement utilisées - distributions logarithmiquement normales, exponentielles, Weibull-Gnedenko, gamma. Jetons un coup d'œil à ces familles. Valeur aléatoire X a une distribution log-normale si la variable aléatoire Oui= journal X a une distribution normale. Puis Z=ln X = 2,3026…Oui a aussi une distribution normale
N(une 1
,σ 1), où ln X- un algorithme naturel X. La densité de la distribution log-normale est : Il résulte du théorème central limite que le produit X =
X 1
X 2
…
X n variables aléatoires positives indépendantes X je,
je = 1, 2,…, n, en gros n
peut être approximée par une distribution log-normale. En particulier, le modèle multiplicatif de formation des salaires ou des revenus conduit à recommander d'approximer les distributions des salaires et des revenus par des lois logarithmiquement normales. Pour la Russie, cette recommandation s'est avérée justifiée - les statistiques le confirment. Il existe d'autres modèles probabilistes qui conduisent à la loi log-normale. Un exemple classique d'un tel modèle est donné par A.N. les broyeurs à boulets ont une distribution log-normale. Passons à une autre famille de distributions, largement utilisée dans diverses méthodes de prise de décision probabiliste-statistique et autres recherches appliquées, la famille des distributions exponentielles. Commençons par un modèle probabiliste qui conduit à de telles distributions. Pour ce faire, considérons le "flux d'événements", c'est-à-dire une séquence d'événements se produisant les uns après les autres à un moment donné. Exemples : flux d'appels au central téléphonique ; le flux de pannes d'équipements dans la chaîne technologique ; flux de défaillances de produits lors des tests de produits ; le flux des demandes des clients vers l'agence bancaire ; le flux d'acheteurs demandant des biens et des services, etc. Dans la théorie des flux d'événements, un théorème similaire au théorème central limite est valide, mais il ne traite pas de la sommation de variables aléatoires, mais de la sommation des flux d'événements. On considère un flux total composé d'un grand nombre de flux indépendants, dont aucun n'a d'effet prédominant sur le flux total. Par exemple, le flux d'appels arrivant au central téléphonique est composé d'un grand nombre de flux d'appels indépendants provenant d'abonnés individuels. Il est prouvé que dans le cas où les caractéristiques des flux ne dépendent pas du temps, le flux total est complètement décrit par un nombre - l'intensité du flux. Pour le débit total, considérons une variable aléatoire X- la longueur de l'intervalle de temps entre les événements successifs. Sa fonction de distribution a la forme Cette distribution est appelée distribution exponentielle car la formule (10) implique la fonction exponentielle e -λ
X. La valeur 1/λ est un paramètre d'échelle. Parfois, un paramètre de décalage est également introduit Avec, exponentielle est la distribution d'une variable aléatoire X + c, où la distribution X est donnée par la formule (10). Les distributions exponentielles sont un cas particulier de ce qu'on appelle. Distributions de Weibull-Gnedenko. Ils portent le nom de l'ingénieur W. Weibull, qui a introduit ces distributions dans la pratique de l'analyse des résultats des tests de fatigue, et du mathématicien BV Gnedenko (1912-1995), qui a reçu des distributions telles que limitantes lors de l'étude du maximum du test. résultats. Laisser X- une variable aléatoire qui caractérise la durée de fonctionnement d'un produit, système complexe, élément (ie ressource, temps de fonctionnement à l'état limite, etc.), la durée de fonctionnement d'une entreprise ou la vie d'un être vivant, etc. Le taux d'échec joue un rôle important où F(X)
et F(X)
- fonction de distribution et densité d'une variable aléatoire X. Décrivons le comportement typique du taux d'échec. L'intervalle de temps entier peut être divisé en trois périodes. Sur le premier d'entre eux, la fonction λ(x) a des valeurs élevées et une nette tendance à diminuer (le plus souvent, il diminue de manière monotone). Ceci peut s'expliquer par la présence dans le lot considéré d'unités de produits présentant des défauts apparents et cachés, qui conduisent à une défaillance relativement rapide de ces unités de produits. La première période est appelée la période de « rodage » (ou « rodage »). Ceci est généralement couvert par la période de garantie. Vient ensuite la période de fonctionnement normal, caractérisée par un taux de panne approximativement constant et relativement faible. La nature des pannes pendant cette période est de nature brutale (accidents, fautes d'opérateurs, etc.) et ne dépend pas de la durée de fonctionnement d'une unité de produit. Enfin, la dernière période de fonctionnement est la période de vieillissement et d'usure. La nature des défaillances au cours de cette période se traduit par des modifications physiques, mécaniques et chimiques irréversibles des matériaux, conduisant à une détérioration progressive de la qualité d'une unité de production et à sa défaillance finale. Chaque période a son propre type de fonction λ(x). Considérez la classe des dépendances de puissance λ(х) = λ0bxb -1
,
(12) où λ 0 >
0 et b> 0 - certains paramètres numériques. Valeurs b < 1, b= 0 et b> 1 correspond au type de taux de défaillance pendant les périodes de rodage, de fonctionnement normal et de vieillissement, respectivement. Relation (11) pour un taux de défaillance donné λ(x)- équation différentielle par rapport à la fonction F(X).
Il découle de la théorie des équations différentielles que En substituant (12) à (13), on obtient que La distribution donnée par la formule (14) est appelée distribution de Weibull - Gnedenko. Dans la mesure où alors il résulte de la formule (14) que la quantité une, donné par la formule (15), est un paramètre d'échelle. Parfois, un paramètre de décalage est également introduit, c'est-à-dire Les fonctions de distribution de Weibull - Gnedenko sont appelées F(X - c), où F(X) est donnée par la formule (14) pour certains λ 0 et b. La densité de la distribution de Weibull - Gnedenko a la forme où une> 0 - paramètre d'échelle, b> 0 - paramètre de formulaire, Avec- paramètre de décalage. Dans ce cas, le paramètre une de la formule (16) est lié au paramètre λ
0 de la formule (14) par le rapport indiqué dans la formule (15). La distribution exponentielle est un cas très particulier de la distribution de Weibull - Gnedenko, correspondant à la valeur du paramètre de forme b = 1. La distribution de Weibull - Gnedenko est également utilisée dans la construction de modèles probabilistes de situations dans lesquelles le comportement d'un objet est déterminé par le "maillon le plus faible". Une analogie avec une chaîne est implicite, dont la sécurité est déterminée par le maillon qui a la plus faible résistance. En d'autres termes, laissez X 1
,
X 2
,…,
X n sont des variables aléatoires indépendantes identiquement distribuées, X(1)=min( X 1 , X 2 ,…, X n), X(n)=maxi( X 1 , X 2 ,…, X n). Dans un certain nombre de problèmes appliqués, un rôle important est joué par X(1)
et X(n)
, en particulier, lors de l'étude des valeurs maximales possibles ("records") de certaines valeurs, par exemple, les paiements d'assurance ou les pertes dues aux risques commerciaux, lors de l'étude des limites d'élasticité et d'endurance de l'acier, un certain nombre de caractéristiques de fiabilité, etc. On montre que pour n grand les distributions X(1)
et X(n)
, en règle générale, sont bien décrites par les distributions de Weibull-Gnedenko. Contributions fondamentales à l'étude des distributions X(1)
et X(n)
a été introduit par le mathématicien soviétique B.V. Gnedenko. Les travaux de V. Weibull, E. Gumbel, V.B. Nevzorova, E.M. Kudlaev et de nombreux autres spécialistes. Passons à la famille des distributions gamma. Ils sont largement utilisés en économie et en gestion, en théorie et en pratique de la fiabilité et des essais, dans divers domaines de la technologie, de la météorologie, etc. En particulier, dans de nombreuses situations, la distribution gamma est soumise à des grandeurs telles que la durée de vie totale du produit, la longueur de la chaîne de particules de poussière conductrices, le temps nécessaire au produit pour atteindre l'état limite lors de la corrosion, la durée de fonctionnement temps jusqu'à kème refus, k= 1, 2, …, etc... L'espérance de vie des patients atteints de maladies chroniques, le temps nécessaire pour obtenir un certain effet dans le traitement ont dans certains cas une distribution gamma. Cette distribution est la plus adéquate pour décrire la demande dans les modèles économiques et mathématiques de gestion des stocks (logistique). La densité de la distribution gamma a la forme La densité de probabilité dans la formule (17) est déterminée par trois paramètres une,
b,
c, où une>0, b>0. Où une est un paramètre de formulaire, b- paramètre d'échelle et Avec- paramètre de décalage. Facteur 1/Γ(a) est une normalisation, elle est introduite afin de Ici Γ(a)- une des fonctions spéciales utilisées en mathématiques, dite "fonction gamma", par laquelle la distribution donnée par la formule (17) est également nommée, A un fixe une la formule (17) définit une famille de distributions à décalage d'échelle générée par une distribution de densité La distribution de la forme (18) est appelée distribution gamma standard. Il est obtenu à partir de la formule (17) avec b= 1 et Avec= 0. Un cas particulier de distributions gamma à une= 1 sont des distributions exponentielles (avec λ = 1/b). Au naturel une et Avec=0 les distributions gamma sont appelées distributions d'Erlang. D'après les travaux du scientifique danois K.A. Erlang (1878-1929), employé de la compagnie de téléphone de Copenhague, qui a étudié en 1908-1922. le fonctionnement des réseaux téléphoniques, le développement de la théorie des files d'attente a commencé. Cette théorie est engagée dans la modélisation probabiliste-statistique de systèmes dans lesquels le flux de requêtes est desservi afin de prendre des décisions optimales. Les distributions Erlang sont utilisées dans les mêmes domaines d'application que les distributions exponentielles. Ceci est basé sur le fait mathématique suivant : la somme de k variables aléatoires indépendantes distribuées exponentiellement avec les mêmes paramètres λ et Avec, a une distribution gamma avec paramètre de forme un =k, paramètre d'échelle b= 1/λ et le paramètre de décalage cc. À Avec= 0 on obtient la distribution d'Erlang. Si la variable aléatoire X a une distribution gamma avec paramètre de forme une tel que ré = 2
une- un nombre entier, b= 1 et Avec= 0, puis 2 X a une distribution du chi carré avec ré degrés de liberté. Valeur aléatoire X avec gvmma-distribution a les caractéristiques suivantes : Valeur attendue M(X) =un B +
c, dispersion ré(X) =
σ
2
=
un B 2
, Le coefficient de variation asymétrie Excès La distribution normale est un cas extrême de la distribution gamma. Plus précisément, soit Z une variable aléatoire avec une distribution gamma standard donnée par la formule (18). Puis pour tout nombre réel X, où F(x)- fonction de distribution normale standard N(0,1). En recherche appliquée, d'autres familles paramétriques de distributions sont également utilisées, dont le système de courbes de Pearson, les séries d'Edgeworth et de Charlier sont les plus connues. Ils ne sont pas considérés ici. Discret distributions utilisées dans les méthodes probabilistes-statistiques de prise de décision. Le plus souvent, trois familles de distributions discrètes sont utilisées - binomiales, hypergéométriques et de Poisson, ainsi que quelques autres familles - géométriques, binomiales négatives, multinomiales, hypergéométriques négatives, etc. Comme déjà mentionné, la distribution binomiale a lieu dans des essais indépendants, dans chacun desquels avec une probabilité R l'événement apparaît UNE. Si le nombre total d'essais n donné, alors le nombre d'essais Oui, dans lequel l'événement est apparu UNE, a une distribution binomiale. Pour une distribution binomiale, la probabilité d'être accepté comme variable aléatoire Oui valeurs y est défini par la formule Nombre de combinaisons de néléments par y connu de la combinatoire. Pour tous y, sauf pour 0, 1, 2, …, n, on a P(Oui=
y)=
0. Distribution binomiale avec une taille d'échantillon fixe n est fixé par le paramètre p, c'est à dire. les distributions binomiales forment une famille à un paramètre. Ils sont utilisés dans l'analyse d'échantillons de données de recherche, en particulier dans l'étude des préférences des consommateurs, le contrôle sélectif de la qualité des produits selon des plans de contrôle en une étape, lors de tests sur des populations d'individus en démographie, sociologie, médecine, biologie, etc. Si Oui 1
et Oui 2
- variables aléatoires binomiales indépendantes avec le même paramètre p 0
déterminé par des échantillons avec des volumes n 1
et n 2
respectivement, alors Oui 1
+ Oui 2
- variable aléatoire binomiale de distribution (19) avec R = p 0
et n
= n 1
+ n 2
. Cette remarque élargit l'applicabilité de la distribution binomiale, permettant de combiner les résultats de plusieurs groupes de tests, lorsqu'il y a lieu de croire qu'un même paramètre correspond à tous ces groupes. Les caractéristiques de la distribution binomiale ont été calculées précédemment : M(Oui) =
np,
ré(Oui) =
np( 1-
p).
Dans la section "Evénements et probabilités" pour une variable aléatoire binomiale, la loi des grands nombres est démontrée : pour tout le monde . A l'aide du théorème central limite, la loi des grands nombres peut être affinée en indiquant comment Oui/
n diffère de R. Théorème de Moivre-Laplace. Pour tous les nombres a et
b, une<
b, on a où F(X) est une fonction de distribution normale standard avec une moyenne de 0 et une variance de 1. Pour le prouver, il suffit d'utiliser la représentation Oui comme une somme de variables aléatoires indépendantes correspondant aux résultats d'essais individuels, des formules pour M(Oui)
et ré(Oui)
et le théorème central limite. Ce théorème est pour le cas R= ½ a été prouvé par le mathématicien anglais A. Moivre (1667-1754) en 1730. Dans la formulation ci-dessus, il a été prouvé en 1810 par le mathématicien français Pierre Simon Laplace (1749-1827). La distribution hypergéométrique a lieu lors du contrôle sélectif d'un ensemble fini d'objets de volume N selon un attribut alternatif. Chaque objet contrôlé est classé soit comme ayant l'attribut UNE, ou comme ne possédant pas cette fonctionnalité. La distribution hypergéométrique a une variable aléatoire Oui, égal au nombre d'objets ayant l'attribut UNE dans un échantillon aléatoire de volume n, où n<
N. Par exemple, le nombre Oui unités défectueuses de produits dans un échantillon aléatoire de volume nà partir du volume du lot N a une distribution hypergéométrique si n<
N.
Un autre exemple est la loterie. Laissez le signe UNE un ticket est un signe « d'être gagnant ». Laissez tous les billets N,
et une personne a acquis n d'eux. Alors le nombre de tickets gagnants pour cette personne a une distribution hypergéométrique. Pour une distribution hypergéométrique, la probabilité qu'une variable aléatoire Y prenne la valeur y a la forme où ré est le nombre d'objets qui ont l'attribut UNE, dans l'ensemble de volume considéré N. Où y prend des valeurs de max(0, n - (N -
ré)) à min( n,
ré), avec d'autre y la probabilité dans la formule (20) est égale à 0. Ainsi, la distribution hypergéométrique est déterminée par trois paramètres - le volume de la population générale N,
nombre d'objets ré en lui, possédant la caractéristique considérée UNE, et la taille de l'échantillon n.
Échantillonnage aléatoire simple n du volume total N est appelé un échantillon obtenu à la suite d'une sélection aléatoire, dans lequel l'un des ensembles de n objets ont la même probabilité d'être sélectionnés. Les méthodes de sélection aléatoire d'échantillons de répondants (personnes interrogées) ou d'unités de produits à la pièce sont examinées dans les documents instructifs-méthodiques et normatifs-techniques. L'une des méthodes de sélection est la suivante : les objets sont sélectionnés les uns parmi les autres, et à chaque étape chacun des objets restant dans l'ensemble a la même chance d'être sélectionné. Dans la littérature, pour le type d'échantillons considérés, les termes « échantillon aléatoire », « échantillon aléatoire sans remise » sont également utilisés. Puisque les volumes de la population générale (lots) N et échantillons n sont communément connus, alors le paramètre de distribution hypergéométrique à estimer est ré. Dans les méthodes statistiques de gestion de la qualité des produits ré- généralement le nombre d'unités défectueuses dans le lot. La caractéristique de la distribution est également intéressante. ré/
N- niveau de défaut. Pour la distribution hypergéométrique Le dernier facteur dans l'expression de la variance est proche de 1 si N>10
n. Si, en même temps, on fait la substitution p =
ré/
N,
alors les expressions de l'espérance mathématique et de la variance de la distribution hypergéométrique se transformeront en expressions de l'espérance mathématique et de la variance de la distribution binomiale. Ce n'est pas un hasard. On peut montrer que à N>10
n,
où p =
ré/
N.
Le rapport limite est valable et cette relation limite peut être utilisée pour N>10
n.
La troisième distribution discrète largement utilisée est la distribution de Poisson. Une variable aléatoire Y a une distribution de Poisson si où λ est le paramètre de distribution de Poisson, et P(Oui=
y)=
0 pour tous les autres y(pour y=0, 0!=1 est noté). Pour la distribution de Poisson M(Oui)
= λ, ré(Oui)
= λ. Cette distribution porte le nom du mathématicien français C.D. Poisson (1781-1840), qui l'a dérivée pour la première fois en 1837. La distribution de Poisson est un cas extrême de la distribution binomiale, où la probabilité R la mise en œuvre de l'événement est faible, mais le nombre d'essais n Superbe et np= λ. Plus précisément, la relation limite Par conséquent, la distribution de Poisson (dans l'ancienne terminologie "loi de distribution") est souvent aussi appelée la "loi des événements rares". La distribution de Poisson apparaît dans la théorie des flux d'événements (voir ci-dessus). Il est prouvé que pour le flux le plus simple d'intensité constante Λ, le nombre d'événements (appels) survenus pendant le temps t, a une loi de Poisson de paramètre λ = Λ t. Par conséquent, la probabilité qu'avec le temps t aucun événement ne se produira e -
Λ t, c'est à dire. la fonction de distribution de la longueur de l'intervalle entre les événements est exponentielle. La distribution de Poisson est utilisée dans l'analyse des résultats d'enquêtes marketing sélectives auprès des consommateurs, le calcul des caractéristiques opérationnelles des plans de contrôle d'acceptation statistique dans le cas de petites valeurs du niveau d'acceptation de la défectuosité, pour décrire le nombre de pannes d'un processus technologique contrôlé statistiquement par unité de temps, le nombre de "besoins de service" arrivant par unité de temps dans le système de file d'attente, les modèles statistiques d'accidents et de maladies rares, etc. La description d'autres familles paramétriques de distributions discrètes et la possibilité de leur utilisation pratique sont envisagées dans la littérature. Dans certains cas, par exemple, lors de l'étude des prix, des volumes de production ou du temps total entre les défaillances dans les problèmes de fiabilité, les fonctions de distribution sont constantes sur certains intervalles dans lesquels les valeurs des variables aléatoires étudiées ne peuvent pas tomber. Des exemples de variables aléatoires distribuées selon la loi normale sont la taille d'une personne, la masse des poissons pêchés de la même espèce. La distribution normale signifie ce qui suit
: il existe des valeurs de taille humaine, la masse de poissons de la même espèce, qui sont perçues intuitivement comme "normales" (et en fait - moyennes), et elles sont beaucoup plus courantes dans un échantillon suffisamment grand que celles qui diffèrent vers le haut ou vers le bas. La distribution de probabilité normale d'une variable aléatoire continue (parfois la distribution gaussienne) peut être appelée en forme de cloche en raison du fait que la fonction de densité de cette distribution, qui est symétrique par rapport à la moyenne, est très similaire à la coupe d'une cloche ( courbe rouge dans la figure ci-dessus). La probabilité de rencontrer certaines valeurs dans l'échantillon est égale à l'aire du chiffre sous la courbe, et dans le cas d'une distribution normale, on voit que sous le haut de la "cloche" , qui correspond à des valeurs tendant vers la moyenne, la surface, et donc la probabilité, est plus grande que sous les bords. Ainsi, on obtient la même chose qui a déjà été dite : la probabilité de rencontrer une personne de taille "normale", d'attraper un poisson de poids "normal" est plus élevée que pour des valeurs qui diffèrent à la hausse ou à la baisse. Dans de très nombreux cas de pratique, les erreurs de mesure sont réparties selon une loi proche de la normale. Arrêtons-nous à nouveau sur la figure du début de la leçon, qui montre la fonction de densité de la distribution normale. Le graphique de cette fonction a été obtenu en calculant un échantillon de données dans le progiciel STATISTIQUES. Sur celui-ci, les colonnes de l'histogramme représentent des intervalles de valeurs d'échantillon dont la distribution est proche (ou, comme on dit dans les statistiques, ne diffère pas significativement) du graphique de la fonction de densité de distribution normale lui-même, qui est une courbe rouge. Le graphique montre que cette courbe est bien en forme de cloche. La distribution normale est précieuse à bien des égards, car connaissant uniquement la moyenne d'une variable aléatoire continue et l'écart type, vous pouvez calculer toute probabilité associée à cette variable. La distribution normale a l'avantage supplémentaire d'être l'une des plus faciles à utiliser critères statistiques utilisés pour tester des hypothèses statistiques - test t de Student- ne peut être utilisé que dans le cas où les données de l'échantillon obéissent à la loi de distribution normale. La fonction de densité de la distribution normale d'une variable aléatoire continue peut être trouvé à l'aide de la formule : où X- valeur de la variable, - valeur moyenne, - écart-type, e\u003d 2,71828 ... - la base du logarithme naturel, \u003d 3,1416 ... Propriétés de la fonction de densité de distribution normale Les changements de moyenne déplacent la courbe en cloche dans la direction de l'axe Bœuf. Si elle augmente, la courbe se déplace vers la droite, si elle diminue, puis vers la gauche. Si l'écart type change, la hauteur du sommet de la courbe change. Lorsque l'écart-type augmente, le sommet de la courbe est plus haut, lorsqu'il diminue, il est plus bas. Déjà dans ce paragraphe, nous commencerons à résoudre des problèmes pratiques, dont la signification est indiquée dans le titre. Analysons les possibilités que la théorie offre pour résoudre les problèmes. Le concept de départ pour calculer la probabilité qu'une variable aléatoire normalement distribuée tombe dans un intervalle donné est la fonction intégrale de la distribution normale. Fonction de distribution normale intégrale: Cependant, il est difficile d'obtenir des tableaux pour chaque combinaison possible de moyenne et d'écart type. Par conséquent, l'un des moyens simples de calculer la probabilité qu'une variable aléatoire distribuée normalement tombe dans un intervalle donné consiste à utiliser des tables de probabilité pour une distribution normale standardisée. Une distribution normale est appelée distribution standardisée ou normalisée., dont la valeur moyenne est , et l'écart type est . Fonction de densité de la distribution normale standardisée: Fonction cumulative de la distribution normale standardisée: La figure ci-dessous montre la fonction intégrale de la distribution normale standardisée, dont le graphique a été obtenu en calculant un échantillon de données dans le progiciel STATISTIQUES. Le graphique lui-même est une courbe rouge et les valeurs de l'échantillon s'en approchent. Pour agrandir l'image, vous pouvez cliquer dessus avec le bouton gauche de la souris. Standardiser une variable aléatoire signifie passer des unités d'origine utilisées dans la tâche aux unités standardisées. La normalisation est effectuée selon la formule En pratique, toutes les valeurs possibles d'une variable aléatoire ne sont souvent pas connues, de sorte que les valeurs de la moyenne et de l'écart type ne peuvent pas être déterminées avec précision. Ils sont remplacés par la moyenne arithmétique des observations et l'écart type s. La magnitude z exprime les écarts des valeurs d'une variable aléatoire par rapport à la moyenne arithmétique lors de la mesure des écarts-types. La table de probabilité pour la distribution normale standardisée, qui est disponible dans presque tous les livres de statistiques, contient les probabilités qu'une variable aléatoire ayant une distribution normale standard Z prend une valeur inférieure à un certain nombre z. Autrement dit, il tombera dans l'intervalle ouvert de moins l'infini à z. Par exemple, la probabilité que la valeur Z moins de 1,5 est égal à 0,93319. Exemple 1 L'entreprise fabrique des pièces qui ont une durée de vie normalement distribuée avec une moyenne de 1000 et un écart type de 200 heures. Pour une pièce choisie au hasard, calculez la probabilité que sa durée de vie soit d'au moins 900 heures. Solution. Introduisons la première notation : La probabilité souhaitée. Les valeurs de la variable aléatoire sont dans l'intervalle ouvert. Mais on peut calculer la probabilité qu'une variable aléatoire prenne une valeur inférieure à une valeur donnée, et selon l'état du problème, il faut trouver une valeur égale ou supérieure à une valeur donnée. C'est l'autre partie de l'espace sous la courbe en cloche. Par conséquent, afin de trouver la probabilité souhaitée, il est nécessaire de soustraire de l'un la probabilité mentionnée que la variable aléatoire prendra une valeur inférieure au 900 spécifié : Maintenant, la variable aléatoire doit être normalisée. On continue en introduisant la notation : z = (X ≤ 900)
; X= 900 - valeur donnée d'une variable aléatoire ; μ
= 1000 - valeur moyenne ; σ
= 200 - écart type. A partir de ces données, on obtient les conditions du problème : Selon les tables d'une variable aléatoire standardisée (limite d'intervalle) z= −0,5 correspond à la probabilité 0,30854. Soustrayez-le de l'unité et obtenez ce qui est requis dans l'état du problème : Ainsi, la probabilité que la durée de vie de la pièce soit d'au moins 900 heures est de 69 %. Cette probabilité peut être obtenue à l'aide de la fonction MS Excel NORM.DIST (la valeur de la valeur intégrale est 1) : P(X≥900) = 1 - P(X≤900) = 1 - LOI.NORMALE(900; 1000; 200; 1) = 1 - 0,3085 = 0,6915. À propos des calculs dans MS Excel - dans l'un des paragraphes suivants de cette leçon. Exemple 2 Dans certaines villes, le revenu familial annuel moyen est une variable aléatoire normalement distribuée avec une valeur moyenne de 300 000 et un écart type de 50 000. On sait que le revenu de 40 % des familles est inférieur à la valeur UNE. Trouver de la valeur UNE. Solution. Dans ce problème, 40 % n'est rien de plus que la probabilité qu'une variable aléatoire prenne une valeur dans un intervalle ouvert inférieure à une certaine valeur, indiquée par la lettre UNE. Pour trouver la valeur UNE, on compose d'abord la fonction intégrale : Selon la tâche μ
= 300000 - valeur moyenne ; σ
= 50000 - écart type ; X = UNE est la valeur à trouver. Faire l'égalité D'après les tableaux statistiques, on trouve que la probabilité de 0,40 correspond à la valeur de la limite de l'intervalle z = −0,25
. On fait donc l'égalité et trouver sa solution : UNE = 287300
. Réponse : le revenu de 40 % des familles est inférieur à 287 300. Dans de nombreux problèmes, il est nécessaire de trouver la probabilité qu'une variable aléatoire normalement distribuée prenne une valeur dans l'intervalle de z 1 à z 2. C'est-à-dire qu'il tombera dans l'intervalle fermé. Pour résoudre de tels problèmes, il est nécessaire de trouver dans le tableau les probabilités correspondant aux bornes de l'intervalle, puis de trouver la différence entre ces probabilités. Cela nécessite de soustraire la plus petite valeur de la plus grande. Des exemples pour résoudre ces problèmes courants sont les suivants, et il est proposé de les résoudre vous-même, puis vous pourrez voir les bonnes solutions et réponses. Exemple 3 Le bénéfice d'une entreprise pour une certaine période est une variable aléatoire soumise à la loi de distribution normale avec une valeur moyenne de 0,5 million d'u.m. et un écart type de 0,354. Déterminez, avec une précision de deux décimales, la probabilité que le profit de l'entreprise soit de 0,4 à 0,6 u.m. Exemple 4 La longueur de la pièce fabriquée est une variable aléatoire distribuée selon la loi normale avec des paramètres μ
=10 et σ
=0,071 . Trouvez, avec une précision de deux décimales, la probabilité de mariage si les dimensions admissibles de la pièce devaient être de 10 ± 0,05. Indice : dans ce problème, en plus de trouver la probabilité qu'une variable aléatoire tombe dans un intervalle fermé (la probabilité d'obtenir une pièce non défectueuse), une action supplémentaire est requise. permet de déterminer la probabilité que la valeur normalisée Z pas moins -z et pas plus +z, où z- une valeur choisie arbitrairement d'une variable aléatoire normalisée. Une méthode approximative pour vérifier la normalité de la distribution des valeurs d'échantillon est basée sur ce qui suit propriété d'une distribution normale : asymétrie β
1
et coefficient d'aplatissement β
2
zéro. Coefficient d'asymétrie β
1
caractérise numériquement la symétrie de la distribution empirique par rapport à la moyenne. Si l'asymétrie est égale à zéro, alors la moyenne arithmétique, la médiane et le mode sont égaux : et la courbe de densité de distribution est symétrique par rapport à la moyenne. Si le coefficient d'asymétrie est inférieur à zéro (β
1
< 0
), alors la moyenne arithmétique est inférieure à la médiane, et la médiane, à son tour, est inférieure au mode () et la courbe est décalée vers la droite (par rapport à la distribution normale). Si le coefficient d'asymétrie est supérieur à zéro (β
1
> 0
), alors la moyenne arithmétique est supérieure à la médiane, et la médiane, à son tour, est supérieure au mode () et la courbe est décalée vers la gauche (par rapport à la distribution normale). Coefficient d'aplatissement β
2
caractérise la concentration de la distribution empirique autour de la moyenne arithmétique dans la direction de l'axe Oy et le degré de crête de la courbe de densité de distribution. Si le coefficient d'aplatissement est supérieur à zéro, alors la courbe est plus allongée (par rapport à la distribution normale) le long de l'axe Oy(le graphique est plus pointu). Si le coefficient d'aplatissement est inférieur à zéro, alors la courbe est plus aplatie (par rapport à une distribution normale) le long de l'axe Oy(le graphique est plus obtus). Le coefficient d'asymétrie peut être calculé à l'aide de la fonction MS Excel SKRS. Si vous vérifiez un tableau de données, vous devez entrer une plage de données dans une case "Nombre". Le coefficient d'aplatissement peut être calculé à l'aide de la fonction d'aplatissement de MS Excel. Lors de la vérification d'un tableau de données, il suffit également d'entrer la plage de données dans une case "Numéro". Ainsi, comme nous le savons déjà, avec une distribution normale, les coefficients d'asymétrie et d'aplatissement sont égaux à zéro. Mais que se passe-t-il si nous obtenons des coefficients d'asymétrie égaux à -0,14, 0,22, 0,43 et des coefficients d'aplatissement égaux à 0,17, -0,31, 0,55 ? La question est tout à fait juste, car dans la pratique, nous ne traitons que des valeurs approximatives et sélectives d'asymétrie et d'aplatissement, qui sont soumises à une dispersion inévitable et incontrôlable. Il est donc impossible d'exiger une égalité stricte de ces coefficients à zéro, ils doivent seulement être suffisamment proches de zéro. Mais que signifie assez ? Il est nécessaire de comparer les valeurs empiriques reçues avec les valeurs admissibles. Pour ce faire, vous devez vérifier les inégalités suivantes (comparer les valeurs des coefficients modulo avec les valeurs critiques - les limites de la zone de test d'hypothèse). Pour le coefficient d'asymétrie β
1
.Loi de distribution d'une variable aléatoire discrète

Le terme est assez courant ligne
Distribution, mais dans certaines situations, cela semble ambigu, et donc j'adhérerai à la "loi".

![]()
![]()
– ainsi, la probabilité de gagner des unités conventionnelles est de 0,4.
est la probabilité qu'un ticket tiré au sort ne gagne pas.![]()
Espérance mathématique d'une variable aléatoire discrète
![]() respectivement. Alors l'espérance mathématique de cette variable aléatoire est égale à somme des travaux toutes ses valeurs par les probabilités correspondantes :
respectivement. Alors l'espérance mathématique de cette variable aléatoire est égale à somme des travaux toutes ses valeurs par les probabilités correspondantes :![]()

![]()
 (1)
(1)


![]()
![]() . (3)
. (3)![]() (4)
(4)![]() (6)
(6)![]() .
.
![]() ,
,![]() .
.![]() permettent de simplifier la justification des méthodes, les formulations de théorèmes et les formules de calcul.
permettent de simplifier la justification des méthodes, les formulations de théorèmes et les formules de calcul.![]()
![]()
![]()
![]() , à savoir,
, à savoir,![]()
![]()
![]()
![]() ,
,![]() .
.![]()

![]()
![]() Ainsi, si les variables aléatoires X 1
,
X 2
,…,
X n N(m, )
, alors leur moyenne arithmétique
Ainsi, si les variables aléatoires X 1
,
X 2
,…,
X n N(m, )
, alors leur moyenne arithmétique![]()
![]()

 (10)
(10)![]() (11)
(11) (13)
(13) (14)
(14) (16)
(16) (17)
(17)![]()

 (18)
(18)![]()
![]()
![]()
![]()
![]()

 (20)
(20)
![]() ,
,Précédent
 ,
,![]()
La probabilité que la valeur d'une variable aléatoire normalement distribuée tombe dans un intervalle donné
 .
.![]() .
.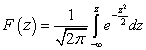 .
.
Intervalle ouvert
![]() .
.![]()
![]() .
.![]()
Intervalle fermé

Une méthode approximative pour vérifier la normalité d'une distribution