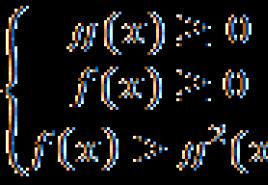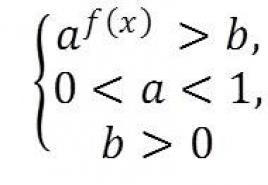Online linear inequality solution with detailed solution. Linear inequalities

The diagram in Figure 5:

And next example: Solve inequality 0.6 2x - 3< 0,36 .

Following the scheme in Figure 5, we obtain
2x - 3> log 0.6 0.36,
2x - 3> 2,
2x> 5,
x> 2.5

Answer: (2,5; +∞) .

Consider the last scheme for solving an inequality of the form and f (x)< b , at a> 0 and b<0 shown in Figure 6:

For example, let's solve the inequality:

We note that no matter what number we substitute for x, the left side of the inequality is always greater than zero, and our expression is less than -8, i.e. and zero, then there are no solutions.

Answer: no solutions.

Knowing how the simplest exponential inequalities are solved, one can proceed to solving exponential inequalities.

Example 1.

Find the largest integer value x satisfying the inequality

Since 6 x is greater than zero (for any x the denominator does not vanish), we multiply both sides of the inequality by 6 x, we get:

440 - 2 6 2x> 8, then
- 2 6 2x> 8 - 440,
- 2 6 2x> - 332,
6 2x< 216,
2x< 3,

x< 1,5. Наибольшее целое число из помежутка (–∞; 1,5) это число 1.

Answer: 1.

Example 2.

Solve inequality 2 2 x - 3 2 x + 2 ≤ 0

We denote 2 x through y, we obtain the inequality y 2 - 3y + 2 ≤ 0, we solve this square inequality.

y 2 - 3y +2 = 0,
y 1 = 1 and y 2 = 2.

The branches of the parabola are directed upwards, we will depict the graph:

Then the solution to the inequality is the inequality 1< у < 2, вернемся к нашей переменной х и получим неравенство 1< 2 х < 2, решая которое и найдем ответ 0 < x < 1.

Answer: (0; 1) .

Example 3... Solve inequality 5 x +1 - 3 x +2< 2·5 x – 2·3 x –1
Let's collect expressions with the same bases in one part of the inequality

5 x +1 - 2.5 x< 3 x +2 – 2·3 x –1

We take out 5 x on the left side of the inequality, and 3 х on the right side of the inequality, and we obtain the inequality

5 x (5 - 2)< 3 х (9 – 2/3),
3 5 x< (25/3)·3 х

We divide both sides of the inequality by the expression 3 3 x, the inequality sign does not change, since 3 3 x is a positive number, we get the inequality:

x< 2 (так как 5/3 > 1).

Answer: (–∞; 2) .

If you have any questions about solving exponential inequalities or want to practice solving similar examples, sign up for my lessons. Tutor Valentina Galinevskaya.

site, with full or partial copying of the material, a link to the source is required.

Solving inequalities online

Before solving inequalities, it is necessary to understand well how the equations are solved.

It does not matter whether the inequality is strict () or non-strict (≤, ≥), the first step is to solve the equation, replacing the inequality sign with equality (=).

Let us explain what it means to solve inequality?

After studying the equations in the student's head, the following picture develops: you need to find such values ​​of the variable at which both sides of the equation take on the same values. In other words, find all the points where equality holds. That's right!

When we talk about inequalities, we mean finding the intervals (segments) on which the inequality holds. If there are two variables in the inequality, then the solution will no longer be intervals, but some areas on the plane. Guess what will be the solution to the inequality in three variables?

How to deal with inequalities?

A universal method for solving inequalities is considered the method of intervals (aka the method of intervals), which consists in determining all intervals within which the specified inequality will be satisfied.

Without going into the type of inequality, in this case it is not the essence, it is required to solve the corresponding equation and determine its roots, followed by the designation of these solutions on the number axis.

How to write down the solution to an inequality correctly?

When you have determined the intervals of solutions to an inequality, you need to correctly write out the solution itself. There is an important nuance - are the boundaries of the intervals included in the solution?

Everything is simple here. If the solution of the equation satisfies the GDV and the inequality is not strict, then the boundary of the interval is included in the solution of the inequality. Otherwise, no.

Considering each interval, the solution to the inequality can be the interval itself, or a half-interval (when one of its boundaries satisfies the inequality), or a segment - an interval together with its boundaries.

An important point

Do not think that only intervals, half-intervals and line segments can be a solution to an inequality. No, the solution may include individual points.

For example, the inequality | x | ≤0 has only one solution - this is the point 0.

And the inequality | x |

What is the inequality calculator for?

The inequality calculator gives the correct final answer. In this case, in most cases, an illustration of a numerical axis or plane is given. It can be seen whether the boundaries of the intervals are included in the solution or not - the points are displayed as filled or punctured.

Thanks to the online inequality calculator, you can check if you found the roots of the equation correctly, marked them on the number axis and checked the inequality condition on the intervals (and boundaries)?

If your answer differs from the answer of the calculator, then you definitely need to double-check your decision and identify the mistake.

Inequality is a numerical ratio that illustrates the magnitude of numbers relative to each other. Inequalities are widely used when searching for quantities in applied sciences. Our calculator will help you deal with such a difficult topic as solving linear inequalities.

What is inequality

Unequal relationships in real life relate to the constant comparison of various objects: higher or lower, further or closer, heavier or lighter. Intuitively or visually, we can understand that one object is larger, higher or heavier than the other, but in fact, we are always talking about comparing numbers that characterize the corresponding values. You can compare objects by any criterion, and in any case, we can compose a numerical inequality.

If the unknown quantities under specific conditions are equal, then for their numerical determination we compose an equation. If not, then instead of the "equal" sign, we can indicate any other ratio between these values. Two numbers or mathematical objects can be greater than ">", less than "<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.

Inequality signs in their modern form were invented by the British mathematician Thomas Garriot, who published a book on unequal ratios in 1631. Signs greater than ">" and less than "<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.

Solving inequalities

Inequalities, like equations, are of different types. Linear, square, logarithmic or exponential unequal relationships are decoupled by various methods. However, regardless of the method, any inequality must first be reduced to a standard form. For this, identical transformations are used, which are identical to the modifications of the equalities.

Identical transformations of inequalities

Such transformations of expressions are very similar to the ghost of equations, but they have nuances that are important to consider when decoupling inequalities.

The first identical transformation is identical to the analogous operation with equalities. To both sides of an unequal ratio, you can add or subtract the same number or expression with an unknown x, while the inequality sign will remain the same. Most often, this method is used in a simplified form as the transfer of the terms of an expression through the inequality sign with a change in the sign of the number to the opposite. This means a change in the sign of the term itself, that is, + R when transferred through any sign of inequality will change to - R and vice versa.

The second transformation has two points:

1. Both sides of an unequal ratio are allowed to be multiplied or divided by the same positive number. In this case, the sign of the inequality itself will not change.
2. Both sides of the inequality are allowed to be divided or multiplied by the same negative number. The sign of the inequality itself will be reversed.

The second identical transformation of inequalities has serious differences with the modification of equations. First, when multiplying / dividing by a negative number, the sign of an unequal expression is always reversed. Second, dividing or multiplying parts of a relation is only allowed by a number, and not by any expression containing an unknown. The fact is that we cannot know for sure whether a number greater or less than zero is hidden behind the unknown, so the second identical transformation is applied to inequalities exclusively with numbers. Let's look at these rules with examples.

Examples of unleashing inequalities

Algebra assignments contain a wide variety of inequality assignments. Let us be given the expression:

6x - 3 (4x + 1)> 6.

First, let's open the brackets and move all unknowns to the left, and all numbers to the right.

6x - 12x> 6 + 3

We need to divide both sides of the expression by −6, so when the unknown x is found, the inequality sign will change to the opposite.

When solving this inequality, we used both identical transformations: transferred all numbers to the right of the sign and divided both sides of the ratio by a negative number.

Our program is a calculator for solving numerical inequalities that do not contain unknowns. The program contains the following theorems for the ratios of three numbers:

• if A< B то A–C< B–C;
• if A> B, then A – C> B – C.

Instead of subtracting members A – C, you can specify any arithmetic operation: addition, multiplication, or division. Thus, the calculator will automatically represent inequalities of sums, differences, products or fractions.

Conclusion

In real life, inequalities are as common as equations. Naturally, in everyday life, knowledge about the resolution of inequalities may not be needed. However, inequalities and their systems are widely used in applied sciences. For example, various studies of the problems of the global economy are reduced to the compilation and unleashing of systems of linear or square inequalities, and some unequal relations serve as an unambiguous way of proving the existence of certain objects. Use our programs to solve linear inequalities or check your own calculations.

Spacing method- a simple way to solve fractional-rational inequalities. This is the name of inequalities containing rational (or fractional-rational) expressions that depend on a variable.

1. Consider, for example, such an inequality

The interval method allows you to solve it in a couple of minutes.

On the left side of this inequality is a fractional rational function. Rational, because it contains no roots, no sines, no logarithms - only rational expressions. On the right is zero.

The interval method is based on the following property of a fractional rational function.

A fractional rational function can change sign only at those points at which it is equal to zero or does not exist.

Let us recall how the square trinomial is decomposed into factors, that is, an expression of the form.

Where and are the roots of the quadratic equation.

Draw the axis and place the points at which the numerator and denominator vanish.

The zeros of the denominator and are punctured points, since at these points the function on the left side of the inequality is undefined (you cannot divide by zero). Numerator zeros and - are filled, as inequality is not strict. For and, our inequality is satisfied, since both of its sides are equal to zero.

These points divide the axis into intervals.

Let us define the sign of the fractional-rational function on the left-hand side of our inequality on each of these intervals. We remember that a fractional rational function can change sign only at those points at which it is equal to zero or does not exist. This means that at each of the intervals between the points where the numerator or denominator vanish, the sign of the expression on the left side of the inequality will be constant - either "plus" or "minus".

And therefore, to determine the sign of the function at each such interval, we take any point belonging to this interval. The one that is convenient for us.
... Take, for example, and check the sign of the expression on the left side of the inequality. Each of the "brackets" is negative. The left side has a sign.

Next span:. Let us check the sign for. We get that the left side has changed the sign to.

Let's take. When the expression is positive, therefore, it is positive throughout the entire interval from to.

For, the left side of the inequality is negative.

Finally, class = "tex" alt = "(! LANG: x> 7"> . Подставим и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .!}

We found at what intervals the expression is positive. It remains to write down the answer:

Answer:.

Please note that the characters in the spaces alternate. This happened because when passing through each point, exactly one of the linear factors changed sign, and the rest kept it unchanged.

We can see that the spacing method is very simple. To solve the fractional-rational inequality by the interval method, we bring it to the form:

Or class = "tex" alt = "(! LANG: \ genfrac () () () (0) (\ displaystyle P \ left (x \ right)) (\ displaystyle Q \ left (x \ right))> 0"> !}, or or .

(on the left - a fractional rational function, on the right - zero).

Then - we mark on the number line the points at which the numerator or denominator vanish.
These points divide the entire number line into intervals, on each of which the fractional rational function preserves its sign.
It remains only to find out its sign at each interval.
We do this by checking the sign of the expression at any point belonging to the given interval. After that, we write down the answer. That's all.

But the question arises: do the signs always alternate? No not always! One must be careful not to place signs mechanically and thoughtlessly.

2. Let's consider one more inequality.

Class = "tex" alt = "(! LANG: \ genfrac () () () (0) (\ displaystyle \ left (x-2 \ right) ^ 2) (\ displaystyle \ left (x-1 \ right) \ left (x-3 \ right))> 0"> !}

Place the points on the axis again. The dots and are punched out because they are the zeros of the denominator. The point is also punctured, since the inequality is strict.

When the numerator is positive, both factors in the denominator are negative. It is easy to check by taking any number from the given interval, for example,. The left side has a sign:

When the numerator is positive; the first factor in the denominator is positive, the second factor is negative. The left side has a sign:

The situation is the same! The numerator is positive, the first factor in the denominator is positive, the second is negative. The left side has a sign:

Finally, with class = "tex" alt = "(! LANG: x> 3"> все множители положительны, и левая часть имеет знак :!}

Answer:.

Why was the alternation of signs broken? Because when passing through a point, the factor "responsible" for it is did not change sign... Consequently, the entire left side of our inequality has not changed its sign either.

Output: if the linear factor is in an even power (for example, in a square), then when passing through the point, the sign of the expression on the left side does not change... In the case of an odd degree, the sign, of course, changes.

3. Let's consider a more complicated case. It differs from the previous one in that the inequality is not strict:

The left side is the same as in the previous task. The picture of signs will be the same:

Maybe the answer will be the same? Not! A solution is added This is because for both the left and right sides of the inequality are equal to zero - therefore, this point is a solution.

Answer:.

In the problem for the exam in mathematics, this situation is often encountered. This is where applicants fall into the trap and lose points. Be careful!

4. What if the numerator or denominator cannot be linearized? Consider this inequality:

The square trinomial cannot be factorized: the discriminant is negative, there are no roots. But this is good! This means that the sign of the expression is the same for all, and specifically, it is positive. You can read more about this in the article on the properties of a quadratic function.

And now we can divide both sides of our inequality by a value that is positive for all. Let's arrive at an equivalent inequality:

Which is easily solved by the method of intervals.

Please note - we divided both sides of the inequality by the amount that we knew for sure that it was positive. Of course, in the general case, it is not worth multiplying or dividing the inequality by a variable whose sign is unknown.

5 ... Consider another inequality, seemingly quite simple:

I just want to multiply it by. But we are already smart, and we will not do this. After all, it can be both positive and negative. And we know that if both sides of the inequality are multiplied by a negative value, the inequality sign changes.

We will do it differently - we will collect everything in one part and bring it to a common denominator. Zero will remain on the right side:

Class = "tex" alt = "(! LANG: \ genfrac () () () (0) (\ displaystyle x-2) (\ displaystyle x)> 0"> !}

And after that - we will apply interval method.

In the article we will consider solution of inequalities... We will tell you in an accessible way about how to construct a solution to inequalities, with clear examples!

Before considering the solution of inequalities using examples, let's understand the basic concepts.

General information about inequalities

Inequality is called an expression in which functions are connected by relation signs>,. Inequalities are both numerical and alphabetic.
Inequalities with two signs of the relationship are called double, with three - triple, etc. For example:
a (x)> b (x),
a (x) a (x) b (x),
a (x) b (x).
a (x) Inequalities containing the sign> or or are not strict.
Solving inequality is any value of the change at which this inequality is true.
"Solve inequality"means that it is necessary to find many of all its solutions. There are various methods for solving inequalities... For solutions to inequality use the number line, which is infinite. For example, solution of inequality x> 3 is an interval from 3 to +, and the number 3 is not included in this interval, therefore a point on a straight line is indicated by an empty circle, since the inequality is strict.
+
The answer will be: x (3; +).
The value x = 3 is not included in the solution set, so the parenthesis is round. The infinity sign is always surrounded by a parenthesis. The sign means "belonging".
Let's consider how to solve inequalities using another signed example:
x 2
-+
The value x = 2 is included in the set of solutions, therefore the square bracket and a point on the line is indicated by a filled circle.
The answer will be: x)