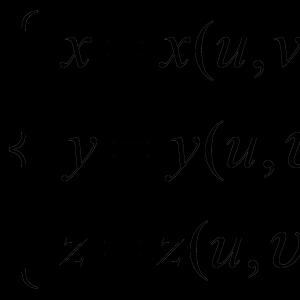Die Gleichung einer geraden Strecke in Segmenten hat die Form. Gleichung einer geraden Linie in Segmenten - Beschreibung, Beispiele, Problemlösung

Wir studieren weiterhin den Abschnitt „Die Gleichung einer geraden Linie in einer Ebene“ und analysieren in diesem Artikel das Thema „Die Gleichung einer geraden Linie in Segmenten“. Wir betrachten nacheinander die Form der Geradengleichung in Strecken, die Konstruktion einer Geraden, die durch diese Gleichung gegeben ist, den Übergang von der allgemeinen Geradengleichung zur Streckengleichung. All dies wird von Beispielen und Analysen zur Problemlösung begleitet.

Auf der Ebene befinde sich ein rechtwinkliges Koordinatensystem O x y.

Eine gerade Linie auf einer Ebene im kartesischen Koordinatensystem O xy ist durch eine Gleichung der Form xa + yb = 1 gegeben, wobei a und b einige reelle Zahlen ungleich Null sind, deren Werte gleich den Längen der Segmente sind abgeschnitten durch die gerade Linie auf den Achsen O x und O y . Die Längen der Segmente werden vom Koordinatenursprung aus betrachtet.

Wie wir wissen, erfüllen die Koordinaten aller Punkte, die zu einer geraden Linie gehören, die durch die Gleichung einer geraden Linie gegeben ist, die Gleichung dieser geraden Linie. Die Punkte a , 0 und 0 , b gehören zu dieser Geraden, da a a + 0 b = 1 ⇔ 1 ≡ 1 und 0 a + b b = 1 ⇔ 1 ≡ 1 . Die Punkte a, 0 und b, 0 befinden sich auf den Koordinatenachsen O x und O y und sind vom Ursprung um a- und b-Einheiten entfernt. Die Richtung, in die Sie die Länge des Segments verschieben möchten, wird durch das Zeichen bestimmt, das vor den Zahlen a und b steht. Das Zeichen „-“ bedeutet, dass die Länge des Segments in negativer Richtung der Koordinatenachse aufgetragen werden muss.

Lassen Sie uns all dies erklären, indem wir die Linien relativ zu einem festen kartesischen Koordinatensystem O x y in einer schematischen Zeichnung platzieren. Aus der Geradengleichung in den Strecken x a + y b = 1 wird eine Gerade im kartesischen Koordinatensystem O x y konstruiert. Dazu müssen wir die Punkte a, 0 und b, 0 auf den Achsen markieren und diese Punkte dann mit einem Lineal mit einer Linie verbinden.

Die Zeichnung zeigt Fälle, in denen die Zahlen a und b unterschiedliche Vorzeichen haben und daher die Längen der Segmente in unterschiedlichen Richtungen der Koordinatenachsen aufgetragen sind.

Betrachten Sie ein Beispiel.

Beispiel 1

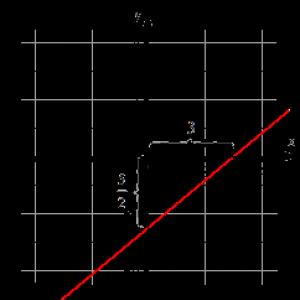
Die Gerade ist durch die Geradengleichung in Segmenten der Form x 3 + y - 5 2 = 1 gegeben. Diese Linie muss in der Ebene im kartesischen Koordinatensystem O x y aufgebaut werden.

Lösung

Mit der Segmentgleichung einer Geraden bestimmen wir die Punkte, durch die die Gerade verläuft. Es ist 3 0 0 - 5 2 . Lassen Sie uns sie markieren und eine Linie ziehen.

Reduktion der allgemeinen Geradengleichung auf die Geradengleichung in Segmenten

Der Übergang von der gegebenen Geradengleichung zur Streckengleichung erleichtert uns die Lösung verschiedener Aufgabenstellungen. Wenn wir die vollständige allgemeine Gleichung einer geraden Linie haben, können wir die Gleichung einer geraden Linie in Segmenten erhalten.

Die vollständige allgemeine Gleichung einer Geraden in der Ebene hat die Form A x + B y + C = 0, wobei A, B und C ungleich Null sind. Wir übertragen die Zahl C auf die rechte Seite der Gleichheit, dividieren beide Teile der resultierenden Gleichheit durch - C. Gleichzeitig senden wir die Koeffizienten für x und y an die Nenner:

A x + B y + C = 0 ⇔ A x + B y = - C ⇔ ⇔ A - C x + B - C y = 1 ⇔ x - C A + y - C B = 1

Um den letzten Übergang zu implementieren, haben wir die Gleichheit p q = 1 q p , p ≠ 0 , q ≠ 0 verwendet.

Damit haben wir den Übergang von der allgemeinen Geradengleichung A x + B y + C = 0 zur Geradengleichung in den Segmenten xa + yb = 1 mit a = - CA , b = vollzogen -CB.

Betrachten wir das folgende Beispiel.

Beispiel 2

Machen wir den Übergang zur Geradengleichung in Segmenten mit der allgemeinen Geradengleichung x - 7 y + 1 2 = 0 .

Lösung

Wir übertragen eine Sekunde auf die rechte Seite der Gleichung x - 7 y + 1 2 = 0 ⇔ x - 7 y = - 1 2 .

Teilen Sie beide Seiten der Gleichung durch - 1 2: x - 7 y = - 1 2 ⇔ 1 - 1 2 x - 7 - 1 2 y = 1 .

Lassen Sie uns die resultierende Gleichheit in die gewünschte Form umwandeln: 1 - 1 2 x - 7 - 1 2 y = 1 ⇔ x - 1 2 + y 1 14 = 1 .

Wir haben die Gleichung einer geraden Linie in Segmenten erhalten.

Antworten: x - 1 2 + y 1 14 = 1

In Fällen, in denen eine gerade Linie durch eine kanonische oder parametrische Gleichung einer geraden Linie in einer Ebene gegeben ist, gehen wir zuerst zur allgemeinen Gleichung einer geraden Linie und dann zur Gleichung einer geraden Linie in Segmenten über.

Es ist einfach, von der Gleichung einer geraden Linie in Segmenten und der allgemeinen Gleichung einer geraden Linie auszugehen: Wir übertragen die Einheit von der rechten Seite der Gleichung einer geraden Linie in Segmenten der Form xa + yb \u003d 1 nach links Seite mit entgegengesetztem Vorzeichen wählen wir die Koeffizienten vor den Unbekannten x und y.

x a + y b = 1 ⇔ x a + y b - 1 = 0 ⇔ 1 a x + 1 b y - 1 = 0

Wir erhalten die allgemeine Geradengleichung, von der wir zu jeder anderen Form der Geradengleichung in einer Ebene übergehen können. Den Übergangsprozess haben wir ausführlich im Thema „Reduzierung der allgemeinen Geradengleichung auf andere Arten von Geradengleichungen“ analysiert.

Beispiel 3

Die Segmentgleichung einer Geraden hat die Form x 2 3 + y - 12 = 1. Es ist notwendig, die allgemeine Gleichung einer geraden Linie in einer Ebene zu schreiben.

Lösung

Es arbeitet nach einem zuvor beschriebenen Algorithmus:

x 2 3 + y - 12 = 1 ⇔ 1 2 3 x + 1 - 12 y - 1 = 0 ⇔ ⇔ 3 2 x - 1 12 y - 1 = 0

Antwort: 3 2 x - 1 12 y - 1 = 0

Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Enter

Geradengleichung , wobei ein und B einige andere reelle Zahlen als Null genannt Gleichung einer Geraden in Segmenten. Dieser Name ist kein Zufall, da die absoluten Werte von Zahlen ein und B gleich den Längen der Segmente, die die Gerade auf den Koordinatenachsen schneidet Ochse und Ey(Segmente werden vom Ursprung aus gezählt). Die Gleichung einer geraden Linie in Segmenten macht es also einfach, diese gerade Linie in einer Zeichnung zu erstellen. Markieren Sie dazu Punkte mit Koordinaten und in einem rechtwinkligen Koordinatensystem in der Ebene und verbinden Sie diese mit einem Lineal mit einer Geraden.

Lassen Sie uns zum Beispiel eine gerade Linie, die durch eine Gleichung gegeben ist, in Segmenten der Form erstellen. Markiere die Punkte und verbinde sie.

Ausführliche Informationen zu dieser Art von Geradengleichung in der Ebene erhalten Sie im Artikel Geradengleichung in Segmenten.

Seitenanfang

Feierabend -

Dieses Thema gehört zu:

Algebra und analytische Geometrie. Das Konzept einer Matrix, Operationen auf Matrizen und ihre Eigenschaften

Das Konzept der Matrixoperationen an Matrizen und ihren Eigenschaften. Eine Matrix ist eine rechteckige Tabelle, die aus Zahlen besteht, die nicht sein können. Die Matrixaddition ist eine elementweise Operation.

Wenn Sie zu diesem Thema weiteres Material benötigen oder nicht fündig geworden sind, empfehlen wir Ihnen die Suche in unserer Werkdatenbank:

Was machen wir mit dem erhaltenen Material:

Wenn sich dieses Material für Sie als nützlich erwiesen hat, können Sie es auf Ihrer Seite in sozialen Netzwerken speichern:

twittern

Alle Themen in diesem Abschnitt:

Definition von Differenzierbarkeit
Die Operation, die Ableitung zu finden, wird Differentiation einer Funktion genannt. Eine Funktion heißt irgendwann differenzierbar, wenn sie an dieser Stelle eine endliche Ableitung hat, und

Differenzierungsregel
Korollar 1. Der konstante Faktor kann aus dem Vorzeichen der Ableitung herausgenommen werden:

Die geometrische Bedeutung der Ableitung. Tangentengleichung
Der Neigungswinkel der Geraden y \u003d kx + b ist der von der Position gemessene Winkel

Die geometrische Bedeutung der Ableitung einer Funktion an einem Punkt
Betrachten Sie die Sekante AB des Graphen der Funktion y = f(x), so dass die Punkte A und B jeweils Koordinaten haben

Lösung
Die Funktion ist für alle reellen Zahlen definiert. Da (-1; -3) also der Kontaktpunkt ist

Notwendige Bedingungen für ein Extremum und hinreichende Bedingungen für ein Extremum
Definition einer steigenden Funktion. Die Funktion y = f(x) wächst auf dem Intervall X, wenn überhaupt

Hinreichende Kriterien für das Extremum einer Funktion
Um die Maxima und Minima der Funktion zu finden, können Sie jedes der drei hinreichenden Zeichen eines Extremums verwenden. Obwohl die erste von ihnen die häufigste und bequemste ist.

Grundlegende Eigenschaften eines bestimmten Integrals. Eigenschaft 1. Die Ableitung eines bestimmten Integrals nach der Obergrenze ist gleich dem Integranden, in den anstelle einer Variablen integriert wird

Newton-Leibniz-Formel (mit Beweis)
Newton-Leibniz-Formel. Sei die Funktion y = f(x) auf einer Strecke stetig und F(x) eine der Stammfunktionen der Funktion auf dieser Strecke

Gegeben sei ein affines Koordinatensystem OXY.

Satz 2.1. Jede gerade l Koordinatensystem OX ist durch eine lineare Gleichung der Form gegeben

EIN x+B j+ C = O, (1)

wobei A, B, C R und A 2 + B 2 0. Umgekehrt definiert jede Gleichung der Form (1) eine gerade Linie.

Gleichung der Form (1) - allgemeine Geradengleichung .

In Gleichung (1) seien alle Koeffizienten A, B und C nicht Null. Dann

Ah-By=-C und .

Lassen Sie uns -C/A=a, -C/B=b bezeichnen. Werden

-Liniensegmentgleichung .

Tatsächlich sind die Zahlen |a| und |b| Geben Sie die Größe der durch eine gerade Linie abgeschnittenen Segmente an l auf der OX- bzw. OY-Achse.

Lassen Sie die Linie l ist durch die allgemeine Gleichung (1) in einem rechtwinkligen Koordinatensystem gegeben und lasse die Punkte M 1 (x 1, y 1) und M 2 (x 2, y 2) gehören l. Dann

EIN x 1 + B beim 1 + C = A x 2 + B beim 2 + C, also A( x 1 -x 2) + B( beim 1 -beim 2) = 0.

Die letzte Gleichheit bedeutet, dass der Vektor \u003d (A, B) orthogonal zum Vektor \u003d (x 1 - x 2, y 1 - y 2) ist. jene. Der Vektor (A, B) wird aufgerufen Normalenvektor der Linie l.

Betrachten Sie den Vektor = (-B, A). Dann

A(-B)+BA=0. jene. ^ .

Daher ist der Vektor \u003d (-B, A) der Richtungsvektor des Scharfen l.

Parametrische und kanonische Gleichungen einer Geraden

Gleichung einer Geraden, die durch zwei gegebene Punkte geht

Gegeben sei die Gerade im affinen Koordinatensystem (0, X, Y) l, sein Richtungsvektor = (m,n) und der Punkt M 0 ( x 0 ,j 0) im Besitz l. Dann gilt für einen beliebigen Punkt M ( x,beim) dieser Linie haben wir

und seitdem .

Wenn wir und bezeichnen

Die Radiusvektoren der Punkte M bzw. M 0

- Gleichung einer Geraden in Vektorform.

Weil =( x,beim), =(x 0 ,beim 0), dann

x= x 0 + mt,

j= j 0 + NT

- Parametergleichung einer Geraden .

Daraus folgt das

- kanonische geradengleichung .

Schließlich, wenn auf einer geraden Linie l zwei Punkte M 1 ( x 1 ,beim 1) und

M2( x 2 ,beim 2), dann ist der Vektor =( x 2 -x 1 ,j 2 -beim 1) ist führen gerader Linienvektor l. Dann

- Gleichung einer Geraden, die durch zwei gegebene Punkte geht.

Gegenseitige Anordnung zweier Geraden.

Geradeaus lassen l 1 und l 2 sind durch ihre allgemeinen Gleichungen gegeben

l 1: Ein 1 x+ Im 1 beim+ С 1 = 0, (1)

l 2: A2 x+B2 beim+ C2 = 0.

Satz. Geradeaus lassen l 1 und l 2 sind durch die Gleichungen (1) gegeben. Dann und nur dann:

1) Linien schneiden sich, wenn es keine Zahl λ gibt, so dass

A 1 = λA 2 , B 1 = λB 2 ;

2) die Linien fallen zusammen, wenn es eine Zahl λ gibt, so dass

A 1 = λA 2 , B 1 = λB 2 , C 1 = λC 2 ;

3) Linien sind verschieden und parallel, wenn es eine Zahl λ gibt, so dass

A 1 \u003d λA 2, B 1 \u003d λB 2, C 1 λC 2.

Bündel von geraden Linien

Ein Haufen gerader Linien ist die Sammlung aller Linien in der Ebene, die durch einen bestimmten Punkt gehen Center Strahl.

Zur Angabe der Balkengleichung genügt es, zwei beliebige Geraden zu kennen l 1 und l 2, die durch die Mitte des Balkens gehen.

Lassen Sie die Linien im affinen Koordinatensystem l 1 und l 2 sind durch die Gleichungen gegeben

l 1:A1 x+B1 j+ C1 = 0,

l 2:A2 x+ B2 j+ C2 = 0.

Die gleichung:

Ein 1 x+B1 j+ С + λ (A 2 x+B2 j+ C) = 0

- die Gleichung eines Linienbündels, definiert durch die Gleichungen l 1 und l 2.

Unter dem Koordinatensystem wird im Folgenden das rechtwinklige Koordinatensystem verstanden .

Bedingungen für Parallelität und Rechtwinkligkeit zweier Geraden

Lassen Sie die Linien l 1 und l 2. mit ihren allgemeinen Gleichungen; = (A 1 ,B 1), = (A 2 ,B 2) sind die Normalenvektoren dieser Geraden; k 1 = tanα 1 , k 2 = tgα 2 – Neigungskoeffizienten; =( m 1 ,n 1), (m 2 ,n 2) sind Richtungsvektoren. Dann direkt l 1 und l 2 sind genau dann parallel, wenn eine der folgenden Bedingungen zutrifft:

oder auch k 1 =k 2 oder .

Lass es jetzt gerade sein l 1 und l 2 sind senkrecht. Dann ist offensichtlich , also A 1 A 2 + B 1 B 2 = 0.

Wenn gerade l 1 und l 2 sind jeweils durch die Gleichungen gegeben

l 1: beim=k 1 x+ B 1 ,

l 2: beim=k 2 x+ B 2 ,

dann ist tgα 2 = tg(90º+α) = .

Daraus folgt das

Schließlich, wenn und die Richtungsvektoren der Linien sind, dann ^ , d.h.

m 1 m 2 + n 1 n 2 = 0

Die letzte Beziehung drückt die notwendige und hinreichende Bedingung aus, dass zwei Ebenen senkrecht zueinander stehen.

Winkel zwischen zwei Geraden

In einem Winkel φ zwischen zwei Linien l 1 und l 2 verstehen wir den kleinsten Winkel, um den eine Linie gedreht werden muss, damit sie parallel zu einer anderen Linie wird oder mit ihr zusammenfällt, also 0 £ φ £

Die Linien seien durch allgemeine Gleichungen gegeben. Es ist klar, dass

cosφ=

Lass es jetzt gerade sein l 1 und l 2 ist durch Gleichungen mit Steigungskoeffizienten gegeben k 1 in k 2 bzw. Dann

Offensichtlich ist das ( x-x 0) + B( beim-beim 0) + C( z-z 0) = 0

Lassen Sie uns die Klammern öffnen und D \u003d -A bezeichnen x 0 - B beim 0 - C z 0 . Werden

EIN x+B j+C z+ D = 0 (*)

- allgemeine Ebenengleichung oder allgemeine Ebenengleichung.

Satz 3.1 Die lineare Gleichung (*) (A 2 + B 2 + C 2 ≠ 0) ist die Gleichung der Ebene und umgekehrt ist jede Gleichung der Ebene linear.

1) D = 0, dann geht die Ebene durch den Ursprung.

2) A \u003d 0, dann ist die Ebene parallel zur OX-Achse

3) A \u003d 0, B \u003d 0, dann ist die Ebene parallel zur OXY-Ebene.

Alle Koeffizienten in der Gleichung seien ungleich Null.

- Gleichung einer Ebene in Segmenten. Die Zahlen |a|, |b|, |c| Geben Sie die Größe der Segmente an, die von der Ebene auf den Koordinatenachsen abgeschnitten werden.

Gleichung einer Geraden in Segmenten

Gegeben sei die allgemeine Geradengleichung:

Die Gleichung einer geraden Linie in Segmenten, wobei die Segmente sind, die die gerade Linie auf den entsprechenden Koordinatenachsen schneidet.

Konstruieren Sie eine Gerade, die durch die allgemeine Gleichung gegeben ist:

Daraus können Sie die Gleichung dieser Geraden in Segmenten aufbauen:

Gegenseitige Anordnung von Geraden in einer Ebene.

Aussage 1.

In der Reihenfolge für die Linien und gegeben durch die Gleichungen:

Zufällig, notwendig und hinreichend, dass:

Beweis: und stimmen überein, ihre Richtungsvektoren und sind kollinear, d.h.:

Nehmen wir den Punkt M 0 mit diesen Geraden, dann gilt:

Multipliziert man die erste Gleichung mit und addiert zur zweiten, erhält man aufgrund von (2):

Somit sind die Formeln (2), (3) und (4) äquivalent. Es gilt (2), dann sind die Gleichungen des Systems (*) äquivalent, die entsprechenden Geraden fallen zusammen.

Aussage 2.

Die durch die Gleichungen (*) gegebenen Linien und sind parallel und fallen genau dann nicht zusammen, wenn:

Nachweisen:

Lassen Sie sie nicht übereinstimmen:

Inkonsistent, d. h. nach dem Satz von Kronecker-Capelli:

Dies ist nur möglich, wenn:

Das heißt, unter Bedingung (5).

Wenn die erste Gleichheit (5) erfüllt ist, - die Nichterfüllung der zweiten Gleichheit ergibt die Inkonsistenz des Systems (*), die Linien sind parallel und fallen nicht zusammen.

Bemerkung 1.

Polarkoordinatensystem.

Wir legen einen Punkt auf der Ebene fest und nennen ihn Pol. Der vom Pol ausgehende Strahl wird Polachse genannt.

Wir wählen eine Skala zum Messen der Längen von Segmenten und einigen uns darauf, dass die Drehung gegen den Uhrzeigersinn um m als positiv betrachtet wird. Betrachten Sie einen beliebigen Punkt auf einer gegebenen Ebene, bezeichnen Sie ihn mit seinem Abstand zum Pol und nennen Sie ihn den Polarradius. Der Winkel, um den die Polarachse gedreht werden muss, damit sie mit zusammenfällt, wird mit bezeichnet und als Polarwinkel bezeichnet.

Bestimmung 3.

Die Polarkoordinaten eines Punktes sind sein Polarradius und sein Polarwinkel:

Bemerkung 2. am Pol. Der Wert für andere Punkte als einen Punkt wird bis zu einer Laufzeit bestimmt.

Stellen Sie sich ein kartesisches rechtwinkliges Koordinatensystem vor: Der Pol fällt mit dem Ursprung zusammen, und die Polachse fällt mit der positiven Halbachse zusammen. Hier. Dann:

Welche Beziehung besteht zwischen rechteckigen kartesischen und polaren Koordinatensystemen?

Bernoullis Lemniskatengleichung. Schreibe es in Polarkoordinaten auf.

Normalengleichung einer Geraden in einer Ebene. Lassen Sie die Polarachse zusammenfallen mit - der Achse, die durch den Ursprung verläuft. Lassen:

Lassen Sie dann:

Bedingung (**) für einen Punkt:

Gleichung einer Geraden im Polarkoordinatensystem.

Hier - die vom Ursprung bis zur Geraden gezogene Länge, - der Neigungswinkel der Normalen zur Achse.

Gleichung (7) kann umgeschrieben werden:

Normalengleichung einer Geraden in einer Ebene.

Eigenschaften einer Geraden in der euklidischen Geometrie.

Es gibt unendlich viele Linien, die durch jeden Punkt gezogen werden können.

Durch zwei beliebige Punkte, die nicht zusammenfallen, gibt es nur eine Gerade.

Zwei nicht zusammenfallende Linien in der Ebene schneiden sich entweder in einem einzigen Punkt oder sind es

parallel (folgt aus dem vorherigen).

Im dreidimensionalen Raum gibt es drei Möglichkeiten für die relative Position zweier Linien:

• Linien schneiden sich;

• gerade Linien sind parallel;

• Geraden schneiden sich.

Gerade Linie- algebraische Kurve erster Ordnung: im kartesischen Koordinatensystem eine Gerade

ist in der Ebene durch eine Gleichung ersten Grades (lineare Gleichung) gegeben.

Allgemeine Geradengleichung.

Definition. Jede Linie in der Ebene kann durch eine Gleichung erster Ordnung gegeben werden

Ah + Wu + C = 0,

und konstant A, B gleichzeitig nicht gleich Null. Diese Gleichung erster Ordnung wird aufgerufen Allgemeines

Gerade Gleichung. Abhängig von den Werten der Konstanten A, B und MIT Folgende Sonderfälle sind möglich:

. C = 0, A ≠ 0, B ≠ 0- Die Linie geht durch den Ursprung

. A = 0, B ≠0, C ≠0 ( By + C = 0)- Gerade parallel zur Achse Oh

. B = 0, A ≠ 0, C ≠ 0 ( Ax + C = 0)- Gerade parallel zur Achse OU

. B = C = 0, A ≠ 0- Die Linie fällt mit der Achse zusammen OU

. A = C = 0, B ≠ 0- Die Linie fällt mit der Achse zusammen Oh

Die Geradengleichung kann je nach Vorgabe in verschiedenen Formen dargestellt werden

Anfangsbedingungen.

Gleichung einer Geraden durch einen Punkt und einen Normalenvektor.

Definition. In einem kartesischen rechtwinkligen Koordinatensystem ein Vektor mit den Komponenten (A, B)

senkrecht zu der durch die Gleichung gegebenen Linie

Ah + Wu + C = 0.

Beispiel. Finden Sie die Gleichung einer geraden Linie, die durch einen Punkt geht A(1, 2) senkrecht zum Vektor (3, -1).

Lösung. Lassen Sie uns bei A \u003d 3 und B \u003d -1 die Gleichung der geraden Linie zusammenstellen: 3x - y + C \u003d 0. Um den Koeffizienten C zu finden

wir setzen die Koordinaten des gegebenen Punktes A in den resultierenden Ausdruck ein und erhalten somit: 3 - 2 + C = 0

C = -1. Gesamt: die gewünschte Gleichung: 3x - y - 1 \u003d 0.

Gleichung einer Geraden, die durch zwei Punkte geht.

Gegeben seien zwei Punkte im Raum M 1 (x 1 , y 1 , z 1) und M2 (x 2, y 2 , z 2), dann Gerade Gleichung,

diese Punkte durchlaufen:

Wenn einer der Nenner gleich Null ist, sollte der entsprechende Zähler gleich Null gesetzt werden. Auf der

Ebene wird die oben geschriebene Geradengleichung vereinfacht:

wenn x1 ≠ x2 und x = x 1, wenn x1 = x2 .

Fraktion = k namens Neigungsfaktor gerade.

Beispiel. Finden Sie die Gleichung einer geraden Linie, die durch die Punkte A(1, 2) und B(3, 4) verläuft.

Lösung. Wenden wir die obige Formel an, erhalten wir:

Gleichung einer Geraden durch einen Punkt und eine Steigung.

Wenn die allgemeine Gleichung einer geraden Linie Ah + Wu + C = 0 ins Formular bringen:

und benennen , dann wird die resultierende Gleichung aufgerufen

Gleichung einer Geraden mit Steigung k.

Die Gleichung einer Geraden auf einem Punkt und einem Richtungsvektor.

Analog zum Punkt, der die Gleichung einer Geraden durch den Normalenvektor betrachtet, können Sie die Aufgabe eingeben

eine Gerade durch einen Punkt und einen Richtungsvektor einer Geraden.

Definition. Jeder Nicht-Null-Vektor (α 1 , α 2), deren Komponenten die Bedingung erfüllen

Aα 1 + Bα 2 = 0 namens Richtungsvektor der Geraden.

Ah + Wu + C = 0.

Beispiel. Finden Sie die Gleichung einer geraden Linie mit Richtungsvektor (1, -1) und durch den Punkt A(1, 2) verlaufend.

Lösung. Wir suchen die Gleichung der gewünschten Geraden in der Form: Ax + By + C = 0. Laut Definition ist

Koeffizienten müssen die Bedingungen erfüllen:

1 * A + (-1) * B = 0, d.h. A = B.

Dann hat die Geradengleichung die Form: Ax + Ay + C = 0, oder x + y + C / A = 0.

beim x=1, y=2 wir bekommen C/A = -3, d.h. Gewünschte Gleichung:

x + y - 3 = 0

Gleichung einer Geraden in Segmenten.

Wenn in der allgemeinen Gleichung der geraden Linie Ah + Wu + C = 0 C≠0, dann erhalten wir durch Teilen durch -C:

oder wo

Die geometrische Bedeutung der Koeffizienten ist, dass der Koeffizient a die Koordinate des Schnittpunkts ist

gerade mit Achse Oh, ein B- die Koordinate des Schnittpunkts der Linie mit der Achse OU.

Beispiel. Die allgemeine Geradengleichung ist gegeben x - y + 1 = 0. Finden Sie die Gleichung dieser geraden Linie in Segmenten.

C \u003d 1, , a \u003d -1, b \u003d 1.

Normalgleichung einer Geraden.

Wenn beide Seiten der Gleichung Ah + Wu + C = 0 durch Zahl dividieren , welches heisst

normalisierender Faktor, dann bekommen wir

xcosφ + ysinφ - p = 0 -Normalgleichung einer Geraden.

Das Vorzeichen ± des Normierungsfaktors muss so gewählt werden, dass μ * C< 0.

R- die Länge der vom Ursprung zur Linie fallenden Senkrechten,

ein φ - der Winkel, den diese Senkrechte mit der positiven Richtung der Achse bildet Oh.

Beispiel. Gegeben sei die allgemeine Geradengleichung 12x - 5y - 65 = 0. Erforderlich, um verschiedene Arten von Gleichungen zu schreiben

diese Gerade.

Die Gleichung dieser Geraden in Segmenten:

Die Gleichung dieser Geraden mit Steigung: (durch 5 teilen)

Gleichung einer geraden Linie:

cos φ = 12/13; sin φ= -5/13; p=5.

Zu beachten ist, dass nicht jede Gerade durch eine Segmentgleichung dargestellt werden kann, z. B. Geraden,

parallel zu den Achsen oder durch den Ursprung gehend.

Winkel zwischen Linien in einer Ebene.

Definition. Wenn zwei Zeilen angegeben sind y \u003d k 1 x + b 1, y \u003d k 2 x + b 2, dann der spitze Winkel zwischen diesen Linien

wird definiert als

Zwei Geraden sind parallel, wenn k1 = k2. Zwei Geraden sind senkrecht

wenn k1 \u003d -1 / k2 .

Satz.

Direkte Ah + Wu + C = 0 und A 1 x + B 1 y + C 1 \u003d 0 sind parallel, wenn die Koeffizienten proportional sind

A 1 \u003d λA, B 1 \u003d λB. Wenn auch С 1 \u003d λС, dann fallen die Linien zusammen. Koordinaten des Schnittpunktes zweier Geraden

werden als Lösung des Gleichungssystems dieser Geraden gefunden.

Die Gleichung einer Geraden, die durch einen gegebenen Punkt verläuft, steht senkrecht auf einer gegebenen Geraden.

Definition. Eine Linie, die durch einen Punkt verläuft M 1 (x 1, y 1) und senkrecht zur Linie y = kx + b

dargestellt durch die Gleichung:

Der Abstand von einem Punkt zu einer Linie.

Satz. Wenn ein Punkt vergeben wird M(x 0, y 0), dann die Entfernung zur Linie Ah + Wu + C = 0 definiert als:

Nachweisen. Lassen Sie den Punkt M 1 (x 1, y 1)- Die Basis der Senkrechten fällt vom Punkt ab m für ein gegebenes

Direkte. Dann der Abstand zwischen den Punkten m und M 1:

(1)

Koordinaten x 1 und 1 kann als Lösung des Gleichungssystems gefunden werden:

Die zweite Gleichung des Systems ist die Gleichung einer geraden Linie, die senkrecht durch einen gegebenen Punkt M 0 verläuft

gegebene Zeile. Wenn wir die erste Gleichung des Systems in die Form umwandeln:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

dann erhalten wir beim Lösen:

Setzen wir diese Ausdrücke in Gleichung (1) ein, finden wir:

Der Satz ist bewiesen.