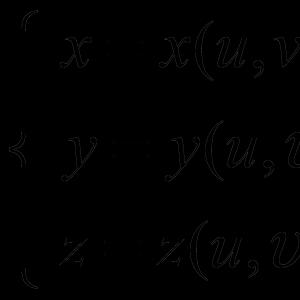Tangentenebene und Flächennormale. Ebene tangential zur Oberfläche Normale und tangentiale Ebenen zur Oberfläche

Download von Depositfiles

4. THEORIE DER OBERFLÄCHEN.

4.1 GLEICHUNGEN VON OBERFLÄCHEN.

Eine Oberfläche im 3D-Raum kann definiert werden:

1) implizit: F ( x , j , z ) =0 (4.1)

2) ausdrücklich: z = F ( x , j ) (4.2)

3) parametrisch: (4.3)

oder:
(4.3’)

wo sind skalare argumente
manchmal auch als krummlinige Koordinaten bezeichnet. Zum Beispiel eine Kugel
Es ist bequem, in sphärischen Koordinaten anzugeben:
.

4.2 TANGENTEBENE UND NORMAL ZUR OBERFLÄCHE.

Liegt die Gerade auf der Fläche (4.1), so erfüllen die Koordinaten ihrer Punkte die Flächengleichung:

Differenzieren wir diese Identität, erhalten wir:

(4.4)

oder
(4.4 ’ )

an jedem Punkt der Kurve auf der Oberfläche. Damit ist der Gradientenvektor an nicht-singulären Punkten der Fläche (an denen die Funktion (4.5) differenzierbar ist und
) steht senkrecht zu den Tangentenvektoren an beliebige Linien auf der Fläche, kann also als Normalenvektor zur Formulierung der Gleichung der Tangentialebene im Punkt M verwendet werden 0 (x 0 , j 0 , z 0 ) Oberflächen

(4.6)

und als Richtungsvektor in der Normalengleichung:

(4.7)

Bei expliziter (4.2) Zuordnung der Fläche nehmen die Gleichungen der Tangentialebene bzw. der Normalen die Form an:

(4.8)

und
(4.9)

In der parametrischen Darstellung der Fläche (4.3) sind die Vektoren
liegen in der Tangentialebene und die Gleichung der Tangentialebene kann geschrieben werden als:

(4.10)

und ihr Vektorprodukt kann als Richtungsnormalenvektor genommen werden:

und die Normalgleichung kann geschrieben werden als:

(4.11)

wo
- Parameterwerte entsprechend Punkt M 0 .

Wir beschränken uns im Folgenden darauf, nur die Punkte der Fläche zu betrachten, an denen die Vektoren liegen

sind ungleich Null und nicht parallel.

Beispiel 4.1 Stellen Sie die Gleichungen der Tangentialebene und der Normalen im Punkt M auf 0 (1,1,2) auf die Oberfläche des Rotationsparaboloids
.

Lösung: Da die Paraboloidgleichung explizit gegeben ist, müssen wir nach (4.8) und (4.9) finden
am Punkt M 0 :

, und am Punkt M 0
. Dann ist die Gleichung der Tangentialebene im Punkt M 0 nimmt die Form an:

2(x -1)+2(j -1)-(z-2)=0 oder 2 x +2 j -z - 2=0 und die normale Gleichung
.

Beispiel 4.2 Stellen Sie die Gleichungen der Tangentialebene und der Normalen an einem beliebigen Punkt auf der Schraubenlinie auf
, .

Lösung. Hier ,

Tangentenebenengleichung:

oder

Normalgleichungen:

4.3 DIE ERSTE QUADRATISCHE FORM DER OBERFLÄCHE.

Wenn die Oberfläche durch die Gleichung gegeben ist

dann die Kurve
darauf kann durch die Gleichung gegeben werden
(4.12)

Radiusvektor-Differential
entlang der Kurve, die der Verschiebung vom Punkt M entspricht 0 zu einem nahe gelegenen Punkt M, gleich ist

(4.13)

Als
ist das Differential des Kurvenbogens, der derselben Verschiebung entspricht), dann

(4.14)

wo .

Der Ausdruck auf der rechten Seite von (4.14) wird als erste quadratische Form der Fläche bezeichnet und spielt eine große Rolle in der Theorie der Flächen.

Differential integrierenDS von T 0 (entspricht Punkt M 0) bis t (entspricht Punkt M) erhalten wir die Länge des entsprechenden Kurvensegments

(4.15)

Kennt man die erste quadratische Form der Fläche, findet man nicht nur die Längen, sondern auch die Winkel zwischen den Kurven.

Wenn du , dv sind die Differentiale von krummlinigen Koordinaten, die einer infinitesimalen Verschiebung entlang einer Kurve entsprechen, und
— andererseits dann unter Berücksichtigung von (4.13):

(4.16)

Mit der Formel

(4.17)

die erste quadratische Form ermöglicht es, die Fläche einer Region zu berechnen
Oberflächen.

Beispiel 4.3 Finden Sie auf einer Spirale die Länge der Spirale
zwischen zwei Punkten.

Lösung. Denn auf einer Spirale
, dann . An einem Punkt finden
die erste quadratische Form. Bezeichnung undv = T , wir erhalten die Gleichung dieser Helix in der Form . Quadratische Form:

= - die erste quadratische Form.

Hier . In Formel (4.15) in diesem Fall
und Bogenlänge:

4.4 ZWEITE QUADRATISCHE FORM DER OBERFLÄCHE.

Bezeichnen
- Einheitsnormalenvektor zur Oberfläche
:

(4.18) . (4.23)

Eine Linie auf einer Fläche heißt Krümmungslinie, wenn ihre Richtung an jedem Punkt die Hauptrichtung ist.

4.6 DAS KONZEPT DER GODÄTISCHEN LINIEN AUF DER OBERFLÄCHE.

Definition 4.1 . Eine Kurve auf einer Fläche heißt Geodäte, wenn ihre Hauptnormale ist an jedem Punkt, an dem die Krümmung nicht Null ist, mit der Normalen zusammenfällt zu der Oberfläche.

Durch jeden Punkt der Oberfläche in beliebiger Richtung verläuft und nur eine Geodäte. Auf einer Kugel sind beispielsweise Großkreise Geodäten.

Eine Parametrisierung einer Oberfläche wird als semi-geodätisch bezeichnet, wenn eine Familie von Koordinatenlinien aus Geodäten besteht und die andere orthogonal dazu ist. Zum Beispiel auf den Kugelmeridianen (Geodäten) und Parallelkreisen.

Eine Geodäte auf einem ausreichend kleinen Segment ist die kürzeste unter allen Kurven in ihrer Nähe, die dieselben Punkte verbinden.

An einem Punkt und hat kontinuierliche partielle Ableitungen an sich, von denen mindestens eine nicht verschwindet, dann befindet sich in der Nähe dieses Punktes die durch Gleichung (1) gegebene Oberfläche richtige Oberfläche.

Zusätzlich zum oben genannten implizite Art der Einstellung Oberfläche definierbar deutlich, wenn eine der Variablen, z. B. z, durch die anderen ausgedrückt werden kann:

Gibt es auch parametrisch Zuordnungsmethode. In diesem Fall wird die Oberfläche durch das Gleichungssystem bestimmt:

Das Konzept einer einfachen Oberfläche

Genauer, einfache Oberfläche ist das Bild einer homöomorphen Abbildung (d. h. einer Eins-zu-Eins- und gegenseitig kontinuierlichen Abbildung) des Inneren des Einheitsquadrats. Dieser Definition kann ein analytischer Ausdruck gegeben werden.

Gegeben sei ein Quadrat auf einer Ebene mit rechtwinkligem Koordinatensystem u und v , dessen Koordinaten der inneren Punkte die Ungleichungen 0 erfüllen< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

Ein Beispiel einfache Oberfläche ist eine Halbkugel. Das ganze Areal nicht einfache Oberfläche. Dies erfordert eine weitere Verallgemeinerung des Begriffs einer Oberfläche.

Eine Teilmenge des Raums, in der jeder Punkt eine Nachbarschaft hat einfache Oberfläche, wird genannt richtige Oberfläche .

Oberfläche in der Differentialgeometrie

Helikoid

Katenoid

Die Metrik bestimmt nicht eindeutig die Form der Oberfläche. Beispielsweise fallen die Metriken eines Helicoids und eines Katenoids bei geeigneter Parametrisierung zusammen, dh es besteht eine Korrespondenz zwischen ihren Bereichen, die alle Längen erhält (Isometrie). Eigenschaften, die bei isometrischen Transformationen erhalten bleiben, werden aufgerufen innere Geometrie Oberflächen. Die innere Geometrie hängt nicht von der Lage der Oberfläche im Raum ab und ändert sich nicht, wenn sie ohne Zug und Druck gebogen wird (z. B. wenn ein Zylinder zu einem Kegel gebogen wird).

Metrische Koeffizienten bestimmen nicht nur die Längen aller Kurven, sondern allgemein die Ergebnisse aller Messungen innerhalb der Oberfläche (Winkel, Flächen, Krümmung usw.). Daher bezieht sich alles, was nur von der Metrik abhängt, auf die innere Geometrie.

Normaler und normaler Abschnitt

Normalenvektoren an Oberflächenpunkten

Eines der Hauptmerkmale einer Oberfläche ist ihre normal- Einheitsvektor senkrecht zur Tangentialebene an einem gegebenen Punkt:

Das Vorzeichen der Normalen hängt von der Wahl der Koordinaten ab.

Der Schnitt einer Fläche durch eine Ebene, die die Normale enthält (an einem bestimmten Punkt), bildet eine bestimmte Kurve auf der Fläche, die als bezeichnet wird normaler Abschnitt Oberflächen. Die Hauptnormale für einen Normalschnitt fällt mit der Normalen zur Oberfläche (bis auf ein Vorzeichen) zusammen.

Ist die Kurve auf der Fläche kein Normalschnitt, so bildet ihre Hauptnormale mit der Flächennormalen einen Winkel θ. Dann die Krümmung k Die Kurve hängt mit der Krümmung zusammen k n Normalschnitt (mit gleicher Tangente) Formel von Meunier:

Die Koordinaten des Normalenvektors für verschiedene Arten der Flächenangabe sind in der Tabelle angegeben:

	Normalkoordinaten an einem Oberflächenpunkt
implizite Zuweisung
explizite Zuordnung
parametrische Aufgabe

Krümmung

Für unterschiedliche Richtungen an einem bestimmten Punkt auf der Oberfläche wird eine unterschiedliche Krümmung des Normalschnitts erhalten, die als bezeichnet wird normale Krümmung; sie erhält ein Pluszeichen, wenn die Hauptnormale der Kurve in die gleiche Richtung wie die Flächennormale geht, oder ein Minuszeichen, wenn die Richtungen der Normalen entgegengesetzt sind.

Im Allgemeinen gibt es an jedem Punkt der Oberfläche zwei senkrecht zueinander stehende Richtungen e 1 und e 2 , in der die normale Krümmung die minimalen und maximalen Werte annimmt; Diese Richtungen werden aufgerufen hauptsächlich. Eine Ausnahme ist der Fall, wenn die normale Krümmung in allen Richtungen gleich ist (z. B. in der Nähe einer Kugel oder am Ende eines Rotationsellipsoids), dann sind alle Richtungen in einem Punkt Hauptrichtungen.

Flächen mit negativer (links), Null- (Mitte) und positiver (rechts) Krümmung.

Normale Krümmungen in Hauptrichtungen werden genannt Hauptkrümmungen; bezeichnen wir sie mit κ 1 und κ 2 . Größe:

K= κ 1 κ 2

namens Gaußsche Krümmung, volle Krümmung oder einfach Krümmung Oberflächen. Es gibt auch den Begriff Krümmungsskalar, was das Ergebnis der Faltung des Krümmungstensors impliziert; in diesem Fall ist der Krümmungsskalar doppelt so groß wie die Gaußsche Krümmung.

Die Gaußsche Krümmung kann über eine Metrik berechnet werden und ist daher ein Objekt der intrinsischen Geometrie von Oberflächen (beachten Sie, dass die Hauptkrümmungen nicht für die intrinsische Geometrie gelten). Anhand des Krümmungszeichens können Sie die Punkte der Fläche klassifizieren (siehe Abbildung). Die Krümmung der Ebene ist Null. Die Krümmung einer Kugel mit Radius R ist überall gleich . Es gibt auch eine Oberfläche mit konstanter negativer Krümmung - eine Pseudosphäre.

Geodätische Linien, geodätische Krümmung

Die Kurve auf der Oberfläche heißt geodätische Linie, oder einfach geodätisch, wenn an allen Punkten die Hauptnormale zur Kurve mit der Normalen zur Fläche zusammenfällt. Beispiel: In einer Ebene sind Geodäten gerade Linien und Liniensegmente, auf einer Kugel - Großkreise und ihre Segmente.

Äquivalente Definition: Für eine geodätische Linie ist die Projektion ihrer Hauptnormalen auf die angrenzende Ebene der Nullvektor. Wenn die Kurve keine Geodäte ist, ist die angegebene Projektion ungleich Null; seine Länge heißt geodätische Krümmung k g Kurve auf der Oberfläche. Es besteht ein Zusammenhang:

wo k ist die Krümmung dieser Kurve, k n- Krümmung seines normalen Abschnitts mit derselben Tangente.

Geodätische Linien beziehen sich auf die interne Geometrie. Wir listen ihre wichtigsten Eigenschaften auf.

Eine und nur eine Geodäte verläuft durch einen bestimmten Punkt auf der Oberfläche in einer bestimmten Richtung.
Auf einer ausreichend kleinen Fläche der Oberfläche können immer zwei Punkte durch eine Geodäte verbunden werden, und zwar nur einer. Erläuterung: Auf einer Kugel sind gegenüberliegende Pole durch eine unendliche Anzahl von Meridianen verbunden, und zwei nahe Punkte können nicht nur durch ein Segment eines großen Kreises verbunden werden, sondern auch durch dessen Addition zu einem Vollkreis, sodass nur die Eindeutigkeit beobachtet wird in einem kleinen.
Die geodätische ist die kürzeste. Genauer gesagt: Auf einem kleinen Stück der Oberfläche liegt der kürzeste Weg zwischen gegebenen Punkten entlang der Geodäte.

Platz

Ein weiteres wichtiges Attribut der Oberfläche ist ihre Platz, die nach folgender Formel berechnet wird:

Eine Fläche ist definiert als eine Menge von Punkten, deren Koordinaten eine bestimmte Art von Gleichung erfüllen:

F (x , y , z) = 0 (1) (\displaystyle F(x,\,y,\,z)=0\qquad (1))

Wenn die Funktion F (x , y , z) (\displaystyle F(x,\,y,\,z)) an einem Punkt stetig ist und daran stetige partielle Ableitungen hat, von denen mindestens eine nicht verschwindet, dann befindet sich in der Nähe dieses Punktes die durch Gleichung (1) gegebene Fläche richtige Oberfläche.

Zusätzlich zum oben genannten implizite Art der Einstellung, kann die Oberfläche definiert werden deutlich, wenn eine der Variablen, z. B. z, durch die anderen ausgedrückt werden kann:

z = f (x , y) (1 ′) (\displaystyle z=f(x,y)\qquad (1"))

Strenger, einfache Oberfläche ist das Bild einer homöomorphen Abbildung (d. h. einer Eins-zu-Eins- und gegenseitig kontinuierlichen Abbildung) des Inneren des Einheitsquadrats. Dieser Definition kann ein analytischer Ausdruck gegeben werden.

Ein Beispiel einfache Oberfläche ist eine Halbkugel. Das ganze Areal nicht einfache Oberfläche. Dies erfordert eine weitere Verallgemeinerung des Begriffs einer Oberfläche.

Eine Teilmenge des Raums, in der jeder Punkt eine Nachbarschaft hat einfache Oberfläche, wird genannt richtige Oberfläche .

Oberfläche in der Differentialgeometrie

Helikoid

Katenoid

Metrische Koeffizienten E , F , G (\displaystyle E,\F,\G) bestimmen nicht nur die Längen aller Kurven, sondern generell die Ergebnisse aller Messungen innerhalb der Oberfläche (Winkel, Flächen, Krümmung etc.). Daher bezieht sich alles, was nur von der Metrik abhängt, auf die innere Geometrie.

Normaler und normaler Abschnitt

Normalenvektoren an Oberflächenpunkten

Eines der Hauptmerkmale einer Oberfläche ist ihre normal- Einheitsvektor senkrecht zur Tangentialebene an einem gegebenen Punkt:

m = [ r u ' , r v ' ] | [ r u ' , r v ' ] | (\displaystyle \mathbf (m) =(\frac ([\mathbf (r"_(u)) ,\mathbf (r"_(v)) ])(|[\mathbf (r"_(u)) ,\mathbf (r"_(v)) ]|))).

Das Vorzeichen der Normalen hängt von der Wahl der Koordinaten ab.

Der Schnitt der Oberfläche durch eine Ebene, die die Normale der Oberfläche an einem bestimmten Punkt enthält, bildet eine bestimmte Kurve, die als bezeichnet wird normaler Abschnitt Oberflächen. Die Hauptnormale für einen Normalschnitt fällt mit der Normalen zur Oberfläche (bis auf ein Vorzeichen) zusammen.

Ist die Kurve auf der Fläche kein Normalschnitt, so bildet ihre Hauptnormale mit der Flächennormalen einen Winkel θ (\displaystyle\theta). Dann die Krümmung k (\ displaystyle k) Die Kurve hängt mit der Krümmung zusammen k n (\ displaystyle k_ (n)) Normalschnitt (mit gleicher Tangente) Formel von Meunier:

k n = ± k cos θ (\displaystyle k_(n)=\pm k\,\cos \,\theta )

Die Koordinaten des Normalenvektors für verschiedene Arten der Flächenangabe sind in der Tabelle angegeben:

	Normalkoordinaten an einem Oberflächenpunkt
implizite Zuweisung	(∂ F ∂ x ; ∂ F ∂ y ; ∂ F ∂ z) (∂ F ∂ x) 2 + (∂ F ∂ y) 2 + (∂ F ∂ z) 2 (\displaystyle (\frac (\left(( \frac (\partial F)(\partial x));\,(\frac (\partial F)(\partial y));\,(\frac (\partial F)(\partial z))\right) )(\sqrt (\left((\frac (\partial F)(\partial x))\right)^(2)+\left((\frac (\partial F)(\partial y))\right) ^(2)+\left((\frac (\partial F)(\partial z))\right)^(2)))))
explizite Zuordnung	(− ∂ f ∂ x ; − ∂ f ∂ y ; 1) (∂ f ∂ x) 2 + (∂ f ∂ y) 2 + 1 (\displaystyle (\frac (\left(-(\frac (\partial f )(\partial x));\,-(\frac (\partial f)(\partial y));\,1\right))(\sqrt (\left((\frac (\partial f)(\ partiell x))\right)^(2)+\left((\frac (\partial f)(\partial y))\right)^(2)+1))))
parametrische Aufgabe	(D (y , z) D (u , v) ; D (z , x) D (u , v) ; D (x , y) D (u , v)) (D (y , z) D (u , v)) 2 + (D (z , x) D (u , v)) 2 + (D (x , y) D (u , v)) 2 (\displaystyle (\frac (\left((\frac (D(y,z))(D(u,v)));\,(\frac (D(z,x))(D(u,v)));\,(\frac (D(x ,y))(D(u,v)))\right))(\sqrt (\left((\frac (D(y,z))(D(u,v)))\right)^(2 )+\left((\frac (D(z,x))(D(u,v)))\right)^(2)+\left((\frac (D(x,y))(D( u,v)))\right)^(2)))))

Hier D (y, z) D (u, v) = | y u ′ y v ′ z u ′ z v ′ | , D (z , x) D (u , v) = | z u ' z v ' x u ' x v ' | , D (x, y) D (u, v) = | x u ′ x v ′ y u ′ y v ′ | (\displaystyle (\frac (D(y,z))(D(u,v)))=(\begin(vmatrix)y"_(u)&y"_(v)\\z"_(u) &z"_(v)\end(vmatrix)),\quad (\frac (D(z,x))(D(u,v)))=(\begin(vmatrix)z"_(u)&z" _(v)\\x"_(u)&x"_(v)\end(vmatrix)),\quad (\frac (D(x,y))(D(u,v)))=(\ begin(vmatrix)x"_(u)&x"_(v)\\y"_(u)&y"_(v)\end(vmatrix))).

Alle Ableitungen werden an diesem Punkt genommen (x 0 , y 0 , z 0) (\displaystyle (x_(0),y_(0),z_(0))).

Krümmung

Im Allgemeinen gibt es an jedem Punkt der Oberfläche zwei senkrecht zueinander stehende Richtungen e 1 (\displaystyle e_(1)) und e 2 (\displaystyle e_(2)), in der die normale Krümmung die minimalen und maximalen Werte annimmt; Diese Richtungen werden aufgerufen hauptsächlich. Eine Ausnahme ist der Fall, wenn die normale Krümmung in allen Richtungen gleich ist (z. B. in der Nähe einer Kugel oder am Ende eines Rotationsellipsoids), dann sind alle Richtungen in einem Punkt Hauptrichtungen.

Flächen mit negativer (links), Null- (Mitte) und positiver (rechts) Krümmung.

Normale Krümmungen in Hauptrichtungen werden genannt Hauptkrümmungen; Lassen Sie uns sie bezeichnen κ 1 (\displaystyle \kappa_(1)) und κ 2 (\displaystyle \kappa_(2)). Größe:

K = κ 1 κ 2 (\displaystyle K=\kappa _(1)\kappa _(2))

Der Graph einer Funktion von 2 Variablen z = f(x,y) ist eine Fläche, die auf die XOY-Ebene in den Definitionsbereich der Funktion D projiziert wird.
Betrachten Sie die Oberfläche σ , gegeben durch die Gleichung z = f(x,y) , wobei f(x,y) eine differenzierbare Funktion ist und M 0 (x 0 ,y 0 ,z 0) ein Fixpunkt auf der Oberfläche σ sei, d.h. z0 = f(x0,y0). Termin. Der Online-Rechner dient zum Finden Tangentenebenen- und Flächennormalengleichungen. Die Entscheidung wird im Word-Format getroffen. Wenn Sie die Gleichung der Tangente an die Kurve finden müssen (y = f(x)), müssen Sie diesen Dienst verwenden.

Eingaberegeln für Funktionen:

Alle Variablen werden in Form von x,y,z ausgedrückt

Tangentialebene zur Oberfläche σ an ihrem Punkt m 0 ist die Ebene, in der die Tangenten aller auf der Fläche gezeichneten Kurven liegen σ durch einen Punkt m 0 .
Die Gleichung der Tangentialebene an die Oberfläche, gegeben durch die Gleichung z = f(x,y) am Punkt M 0 (x 0 ,y 0 ,z 0) hat die Form:

z - z 0 \u003d f 'x (x 0, y 0) (x - x 0) + f' y (x 0, y 0) (y - y 0)

Der Vektor wird Oberflächennormalenvektor genannt σ am Punkt M 0 . Der Normalenvektor steht senkrecht auf der Tangentialebene.
Normal zur Oberfläche σ am Punkt m 0 ist eine gerade Linie, die durch diesen Punkt verläuft und die Richtung des Vektors N hat.
Die kanonischen Gleichungen der Normalen zur Oberfläche, gegeben durch die Gleichung z = f(x,y) am Punkt M 0 (x 0 ,y 0 ,z 0), wobei z 0 = f(x 0 ,y 0), haben die Form:

Beispiel 1. Die Oberfläche ist durch die Gleichung x 3 +5y gegeben. Finden Sie die Gleichung der Tangentialebene an die Oberfläche am Punkt M 0 (0;1).
Lösung. Schreiben wir die Tangentengleichungen in allgemeiner Form: z - z 0 \u003d f "x (x 0, y 0, z 0) (x - x 0) + f" y (x 0, y 0, z 0) (y - j 0 )
Durch die Bedingung des Problems x 0 = 0, y 0 = 1, dann z 0 = 5
Finde die partiellen Ableitungen der Funktion z = x^3+5*y:
f" x (x, y) = (x 3 +5 y)" x = 3 x 2
f" x (x, y) = (x 3 +5 y)" y = 5
Am Punkt M 0 (0,1) sind die Werte der partiellen Ableitungen:
f"x(0;1) = 0
f" y (0; 1) = 5
Mit der Formel erhalten wir die Gleichung der Tangentialebene an die Oberfläche am Punkt M 0: z - 5 = 0(x - 0) + 5(y - 1) oder -5 y + z = 0

Beispiel #2. Die Oberfläche ist implizit gegeben durch y 2 -1/2*x 3 -8z. Finden Sie die Gleichung der Tangentialebene an die Oberfläche am Punkt M 0 (1;0;1).
Lösung. Wir finden partielle Ableitungen der Funktion. Da die Funktion implizit gegeben ist, suchen wir Ableitungen nach der Formel:

Für unsere Funktion:

Dann:

Am Punkt M 0 (1,0,1) die Werte partieller Ableitungen:
f "x (1; 0; 1) \u003d -3 / 16
f"y(1;0;1) = 0
Unter Verwendung der Formel erhalten wir die Gleichung der Tangentialebene an die Oberfläche am Punkt M 0: z - 1 \u003d -3 / 16 (x - 1) + 0 (y - 0) oder 3 / 16 x + z- 19 / 16 \u003d 0

Beispiel. Oberfläche σ durch die Gleichung gegeben z= y/x + xy – 5x 3 . Finden Sie die Gleichung der Tangentialebene und der Normalen zur Oberfläche σ am Punkt m 0 (x 0 ,j 0 ,z 0) dazu gehörend, wenn x 0 = –1, j 0 = 2.
Finden wir die partiellen Ableitungen der Funktion z= F(x,j) = y/x + xy – 5x 3:
f x '( x,j) = (y/x + xy – 5x 3)' x \u003d - y / x 2 + j – 15x 2 ;
f y' ( x,j) = (y/x + xy – 5x 3)' y = 1/x + x.
Punkt m 0 (x 0 ,j 0 ,z 0) gehört zur Oberfläche σ , damit wir rechnen können z 0 , Ersetzen des Gegebenen x 0 = -1 und j 0 = 2 in die Oberflächengleichung:

z= y/x + xy – 5x 3

z 0 = 2/(-1) + (–1) 2 – 5 (–1) 3 = 1.
Am Punkt m 0 (–1, 2, 1) Werte partieller Ableitungen:
f x '( m 0) = –1/(-1) 2 + 2 – 15(–1) 2 = –15; fy'( m 0) = 1/(-1) – 1 = –2.
Mit Formel (5) erhalten wir die Gleichung der Tangentialebene an die Oberfläche σ am Punkt m 0:
z – 1= –15(x + 1) – 2(j – 2) z – 1= –15x – 15 – 2ja + 4 15x + 2j + z + 10 = 0.
Mit Formel (6) erhalten wir die kanonischen Gleichungen der Flächennormalen σ am Punkt m 0:

.
Antworten: Gleichung der Tangentialebene: 15 x + 2j + z+ 10 = 0; normale Gleichungen:

Beispiel 1. Gegeben sei eine Funktion z \u003d f (x, y) und zwei Punkte A (x 0, y 0) und B (x 1, y 1). Gefordert: 1) berechne den Wert z 1 der Funktion am Punkt B; 2) Berechnen des ungefähren Werts z 1 der Funktion am Punkt B basierend auf dem Wert z 0 der Funktion am Punkt A, Ersetzen des Inkrements der Funktion während des Übergangs von Punkt A zu Punkt B durch ein Differential; 3) erstelle die Gleichung der Tangentialebene an die Oberfläche z = f(x,y) am Punkt C(x 0 ,y 0 ,z 0).
Lösung.
Wir schreiben die Tangensgleichungen in allgemeiner Form:
z - z 0 \u003d f "x (x 0, y 0, z 0) (x - x 0) + f" y (x 0, y 0, z 0) (y - y 0)
Gemäß der Bedingung des Problems ist x 0 = 1, y 0 = 2, dann z 0 = 25
Finde die partiellen Ableitungen der Funktion z = f(x,y)x^2+3*x*y*+y^2:
f "x (x, y) \u003d (x 2 +3 x y + y 2)" x \u003d 2 x + 3 y 3
f "x (x, y) \u003d (x 2 +3 x y + y 2)" y \u003d 9 x y 2
Am Punkt M 0 (1.2) sind die Werte partieller Ableitungen:
f" x (1; 2) = 26
f" y (1; 2) = 36
Mit der Formel erhalten wir die Gleichung der Tangentialebene an die Oberfläche am Punkt M 0:
z - 25 = 26(x - 1) + 36(y - 2)
oder
-26x-36y+z+73 = 0

Beispiel #2. Schreiben Sie die Gleichungen der Tangentialebene und der Normalen des elliptischen Paraboloids z = 2x 2 + y 2 an den Punkt (1;-1;3).

Definition. Ein Punkt, der auf einer Fläche zweiter Ordnung liegt, die durch die allgemeine Gleichung (1) in Bezug auf die ODSC gegeben ist, wird als nicht-singulär bezeichnet, wenn unter den drei Zahlen: es mindestens eine gibt, die nicht gleich Null ist.

Somit ist ein Punkt, der auf einer Fläche zweiter Ordnung liegt, genau dann nicht singulär, wenn er ihr Mittelpunkt ist, ansonsten, wenn die Fläche konisch ist und der Punkt der Scheitelpunkt dieser Fläche ist.

Definition. Eine Tangente an eine Fläche zweiter Ordnung an einem gegebenen nicht singulären Punkt darauf ist eine gerade Linie, die durch diesen Punkt verläuft, die Fläche zweiter Ordnung an einem Doppelpunkt schneidet oder eine geradlinige Erzeugende der Fläche ist.

Satz 3. Die Tangentenlinien zu einer Fläche zweiter Ordnung an einem gegebenen nicht-singulären Punkt darauf liegen in derselben Ebene, die als Tangentialebene zur Fläche an dem betrachteten Punkt bezeichnet wird. Die Tangentialebenengleichung hat

Nachweisen. Seien , , parametrische Gleichungen einer geraden Linie, die durch einen nicht-singulären Punkt der durch Gleichung (1) gegebenen Fläche zweiter Ordnung verläuft. Durch Einsetzen von , , statt , , , in Gleichung (1) erhalten wir:

Da der Punkt auf der Fläche (1) liegt, finden wir auch aus Gleichung (3) (dieser Wert entspricht dem Punkt ). Damit der Schnittpunkt der Geraden mit der Fläche (1) doppelt ist oder die Gerade ganz auf der Fläche liegt, ist es notwendig und hinreichend, dass die Gleichheit erfüllt ist:

Wenn gleichzeitig:

Dann ist der Schnittpunkt der Geraden mit der Fläche (1) doppelt. Und wenn:

Dann liegt die Leitung vollständig auf der Oberfläche (1).

Aus den Beziehungen (4) und , , folgt, dass die Koordinaten , , jedes Punktes, der auf einer beliebigen Tangente an die Fläche (1) liegt, die Gleichung erfüllen:

Wenn umgekehrt die Koordinaten eines anderen Punktes als diese Gleichung erfüllen, dann erfüllen die Koordinaten , , des Vektors die Beziehung (4), was bedeutet, dass die Linie die betrachtete Oberfläche tangiert.

Da der Punkt ein nichtsingulärer Punkt der Fläche (1) ist, gibt es unter den Zahlen , , mindestens eine, die nicht gleich Null ist; also ist Gleichung (5) eine Gleichung ersten Grades bezüglich . Dies ist die Gleichung der Ebene, die die Oberfläche (1) an einem nicht singulären Punkt tangiert, der darauf gegeben ist.

Basierend auf den kanonischen Gleichungen von Oberflächen zweiter Ordnung ist es einfach, die Gleichungen von Tangentialebenen an ein Ellipsoid, Hyperboloid usw. an einem bestimmten Punkt auf ihnen.

eins). Tangentialebene an Ellipsoid:

2). Tangentialebene an ein- und zweiblättrige Hyperboloide:

3). Tangentialebene an elliptische und hyperbolische Paraboloide:

§ 161. Schnitt einer Tangentialebene mit einer Fläche zweiter Ordnung.

Wir nehmen einen nicht-singulären Punkt der Oberfläche zweiter Ordnung als Koordinatenursprung der ODSC, der Achse, und platzieren ihn in der Ebene, die die Oberfläche am Punkt tangiert. Dann ist in der allgemeinen Oberflächengleichung (1) der freie Term gleich Null: , und die Gleichung der Ebene, die die Oberfläche im Ursprung berührt, sollte wie folgt aussehen: .

Aber die Gleichung der Ebene, die durch den Ursprung geht, hat die Form: .

Und da diese Gleichung mit der Gleichung äquivalent sein muss, dann , , .

Im gewählten Koordinatensystem sollte die Oberflächengleichung (1) also folgendermaßen aussehen:

Umgekehrt, wenn , dann ist Gleichung (6) die Gleichung der Oberfläche, die durch den Koordinatenursprung verläuft, und die Ebene ist die Tangentialebene zu dieser Oberfläche am Punkt . Die Gleichung der Linie, entlang der die Tangentialebene an die Oberfläche an einem Punkt die Oberfläche (6) schneidet, hat die Form:

Wenn . Dies ist eine Invariante in der Invariantentheorie für Linien zweiter Ordnung. Gleichung (7)

Dies ist die zweite Zeile. Durch die Form dieser Linie ist die Invariante daher:

Für sind hier zwei imaginäre Schnittlinien.

Wann - zwei echte Schnittlinien.

Wenn , aber mindestens einer der Koeffizienten , , ungleich Null ist, dann ist die Schnittgerade (7) zwei zusammenfallende Geraden.

Endlich, wenn , dann das Flugzeug

ist ein Teil der gegebenen Fläche, und die Fläche selbst zerfällt daher in ein Ebenenpaar

§ 162. Elliptische, hyperbolische oder parabolische Punkte einer Fläche zweiter Ordnung.

1. Die Tangentialebene an die Fläche zweiter Ordnung lasse sie in einem Punkt entlang zweier gedachter sich schneidender Geraden schneiden. In diesem Fall wird der Punkt als elliptischer Punkt der Oberfläche bezeichnet.

2. Die Tangentialebene an die Oberfläche zweiter Ordnung schneide sie in einem Punkt entlang zweier reeller Linien, die sich im Kontaktpunkt schneiden. In diesem Fall wird der Punkt als hyperbolischer Punkt der Fläche bezeichnet.

3. Die Tangentialebene an die Fläche zweiter Ordnung lasse sie in einem Punkt entlang zweier zusammenfallender Geraden schneiden. In diesem Fall wird der Punkt ein parabolischer Punkt der Oberfläche genannt.

Satz 4. Die Fläche zweiter Ordnung in Bezug auf die ODSC sei durch Gleichung (1) gegeben, und diese Gleichung (1) sei die Gleichung einer realen, nicht zerfallenden Fläche zweiter Ordnung. Dann wenn ; dann sind alle Punkte der Fläche elliptisch.

Nachweisen. Lassen Sie uns ein neues Koordinatensystem einführen, indem wir einen beliebigen nicht-singulären Punkt der gegebenen Fläche als Koordinatenursprung wählen und die Achsen und in der Ebene platzieren, die die Fläche am Punkt tangiert. Gleichung (1) im neuen Koordinatensystem wird transformiert in die Form:

Wo . Lassen Sie uns die Invariante für diese Gleichung berechnen.

Da sich das Vorzeichen beim Übergang von einem ODSC zum anderen nicht ändert, sind die Vorzeichen und entgegengesetzt, also if , then ; und wie aus der Klassifizierung folgt (siehe § 161), schneidet die Tangentialebene an die Oberfläche an einem Punkt die Oberfläche entlang zweier imaginärer Schnittlinien, d.h. ist ein elliptischer Punkt.

2) Ein einschaliges Hyperboloid und ein hyperbolisches Paraboloid bestehen aus hyperbolischen Punkten.

3) Der reelle Kegel zweiter Ordnung (der Scheitel ist ausgeschlossen), elliptische (reelle), hyperbolische und parabolische Zylinder bestehen aus Parabelpunkten.

parabolischer Zylinder.

Um die Position eines parabolischen Zylinders zu bestimmen, genügt es zu wissen:

1) eine Symmetrieebene parallel zu den Generatoren des Zylinders;

2) eine Tangentialebene an den Zylinder, senkrecht zu dieser Symmetrieebene;

3) ein Vektor senkrecht zu dieser Tangentenebene und gerichtet auf die Konkavität des Zylinders.

Wenn die allgemeine Gleichung einen parabolischen Zylinder definiert, kann sie umgeschrieben werden als:

Wählen wir aus m damit das Flugzeug

würden senkrecht zueinander stehen:

Mit diesem Wert m Flugzeug

wird eine Symmetrieebene parallel zu den Generatoren des Zylinders sein.

Ebene

wird die Tangentenebene an den Zylinder sein, senkrecht zur angegebenen Symmetrieebene, und der Vektor

senkrecht zur gefundenen Tangentialebene und auf die Konkavität des Zylinders gerichtet.