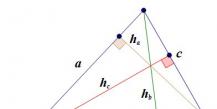
Stranski kot 2 2 osnovna višina. Višina trikotnika

Pri reševanju geometrijskih problemov je koristno slediti takemu algoritmu. Med branjem pogojev naloge

• Naredite risbo. Risba mora čim bolj ustrezati stanju problema, zato je njegova glavna naloga pomagati najti rešitev
• Če želite na risbo postaviti vse podatke iz pogojev naloge
• Zapišite vse geometrijske koncepte, ki se pojavljajo v problemu
• Spomnimo se na vse teoreme, ki se nanašajo na ta koncept.
• Na risbo postavite vsa razmerja med elementi geometrijske figure, ki izhajajo iz teh izrek

Če na primer težava vsebuje besede bisektor kota trikotnika, morate priklicati definicijo in lastnosti bisektorja in na risbi določiti enake ali sorazmerne odseke in kote.

V tem članku boste našli osnovne lastnosti trikotnika, ki jih morate poznati, da uspešno rešite težave.

TRIANGLE.

Območje trikotnika.

1. ,

tukaj je poljubna stran trikotnika, ali je višina spuščena na to stran.

2. ,

tukaj in sta poljubni strani trikotnika, je kot med tema stranima:

3. Formula čaplje:

Tu so dolžine strani trikotnika, je polperimeter trikotnika,

4. ,

tu je polperimeter trikotnika, je polmer vpisanega kroga.

Naj bodo dolžine segmentov tangente.

Nato lahko Heronovo formulo zapišemo na naslednji način:

5.

6. ,

tu so dolžine stranic trikotnika, je polmer opisanega kroga.

Če vzamemo točko na strani trikotnika, ki deli to stran glede na m: n, potem odsek, ki povezuje to točko z vrhom nasprotnega kota, trikotnik deli na dva trikotnika, katerih območja se imenujeta m: n:

Površinsko razmerje takšnih trikotnikov je enako kvadratu koeficienta podobnosti.

Trikotnik Med

To je črta, ki povezuje vrh trikotnika s sredino nasprotne strani.

Trikotnik median  sekajo na eni točki in delijo presečišče v razmerju 2: 1, šteje se od vrha.

Točka preseka mediane pravilnega trikotnika deli mediano na dva segmenta, od katerih je manjši polmer vpisanega kroga, večji pa polmer opisanega kroga.

Polmer opisanega kroga je dvakrat večji od polmera vpisanega kroga: R \u003d 2r

Srednja dolžina  poljuben trikotnik

,

tukaj je mediana, narisana na stran - dolžine strani trikotnika.

Dvokolesnik trikotnika

To je segment bisektorja katerega koli kota trikotnika, ki povezuje vrh tega vogala z nasprotno stranjo.

Dvokolesnik trikotnika  stran razdeli na segmente, sorazmerne s sosednjimi stranmi:

Bisektorji trikotnika  sekajo na eni točki, ki je središče vpisanega kroga.

Vse točke bisektorja kota so enako oddaljene od strani kota.

Višina trikotnika

To je odsek pravokotnika, ki se spusti z vrha trikotnika na nasprotno stran, ali njegovo nadaljevanje. V nejasnem trikotniku je višina, narisana z vrha akutnega kota, zunaj trikotnika.

Višine trikotnika sekajo v eni točki, ki se imenuje ortocenter trikotnika.

Če želite najti višino trikotnikanarisano na stran, morate na poljuben način najti njegovo območje in nato uporabiti formulo:

Središče kroga je bilo okoli trikotnikaleži na presečišču srednjih pravokotnikov, narisanih na stranice trikotnika.

Polmer opisanega kroga trikotnika   je mogoče najti po naslednjih formulah:

Tu so dolžine strani trikotnika, je območje trikotnika.

,

kjer je dolžina strani trikotnika, je nasprotni kot. (Ta formula izhaja iz sinusnega teorema).

Neenakost trikotnika

Vsaka stran trikotnika je manjša od vsote in večja od razlike ostalih dveh.

Vsota dolžin katerih koli dveh strani je vedno večja od dolžine tretje strani:

Nasproti večje strani leži večji kot; nasproti večjega kota leži velika stran:

Če, potem in obratno.

Teorem sinusa:

stranice trikotnika so sorazmerne s sinusi nasprotnih kotov:

Teorem o kosinu:

kvadrat strani trikotnika je vsota kvadratov drugih dveh strani brez dvojnega zmnožaka teh strani s kosinusom kota med njima:

Pravi trikotnik

- gre za trikotnik, katerega eden od kotov je 90 °.

Vsota akutnih kotov desnega trikotnika je 90 °.

Hipotenuza je tista stran, ki leži pod kotom 90 °. Hipotenuza je največja plat.

Pitagorov izrek:

kvadrat hipotenuze je enak vsoti kvadratov nog:

Polmer kroga, vpisanega v pravi trikotnik, je

,

tu - polmer vpisanega kroga, - noge, - hipotenuza:

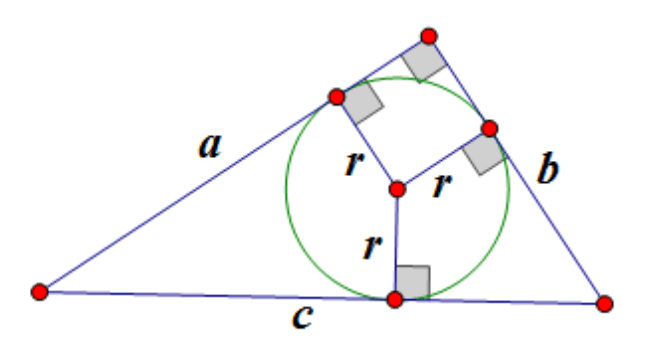
Središče kroga je obrisano blizu pravega trikotnika leži sredi hipotenuze:

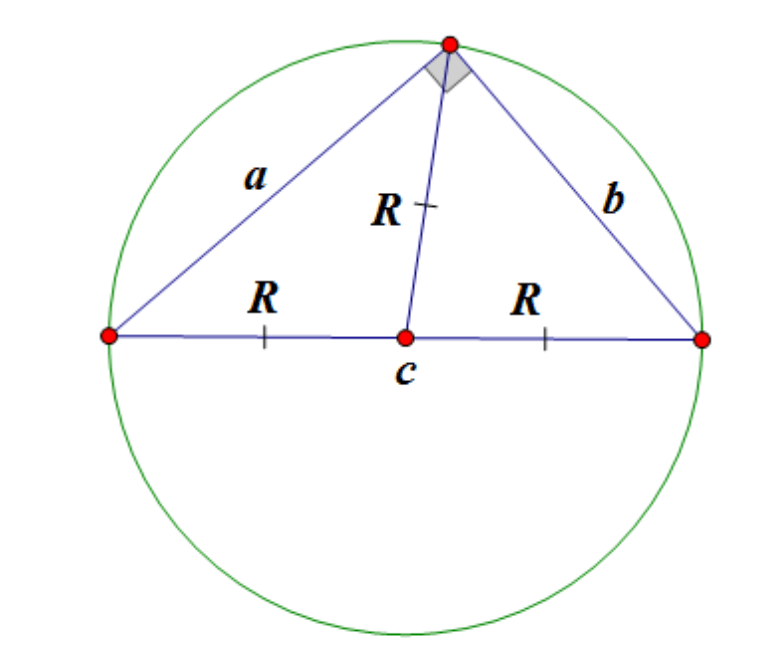
Mediana hipotenuze desnega trikotnikaje enaka polovici hipotenuze.

Opredelitev sinusa, kosinusa, tangenta in kotangenta desnega trikotnika  glej

Razmerje elementov v pravem trikotniku:

Kvadrat višine desnega trikotnika, narisanega od vrha desnega kota, je enak zmnožku štrlečih nog na hipotenuzo:

Kvadrat noge je rezultat hipotenuze na projekciji noge na hipotenuzo:

  Noga, ki leži proti vogalu enako polovici hipotenuze:

Izosceles trikotnik.

Bisektor enakotničnega trikotnika, vlečen na osnovo, sta mediana in višina.

V enakomernem trikotniku so koti na dnu enaki.

Apex kota.

In - strani

In - vogali na dnu.

Višina, bisektor in mediana.

Pozor!   Višina, debelina in srednja črta na strani se ne ujemata.

Pravi trikotnik

(ali enakostranični trikotnik ) je trikotnik, katerega vse strani in koti so enaki drug drugemu.

Območje navadnega trikotnika  je enako

kje je dolžina strani trikotnika.

Središče kroga, vpisanega v navadni trikotnik, sovpada s središčem kroga, ki je obrezan blizu pravilnega trikotnika in leži na presečišču medianov.

Točka presečišča medianih pravilnega trikotnika  srednjo razdeljeno na dva segmenta, od katerih je manjši polmer vpisanega kroga, večji pa polmer opisanega kroga.

Če je eden od kotov enakotničnega trikotnika 60 °, potem je ta trikotnik pravilen.

Srednja črta trikotnika

To je segment, ki povezuje sredino dveh strani.

Na sliki je DE srednja črta trikotnika ABC.

Srednja črta trikotnika je vzporedna s tretjo stranjo in je enaka njeni polovici: DE || AC, AC \u003d 2DE

Zunanji kot trikotnika

To je kot, ki meji na kateri koli vogal trikotnika.

Zunanji kot trikotnika je enak vsoti dveh kotov, ki nista zraven.

Trigonometrične funkcije zunanjega kota:

Znaki enakosti trikotnikov:

1   . Če sta dve strani in kot med njima v enem trikotniku enaki dvema stranema in kot med njimi drugega trikotnika, sta taka trikotnika enaka.

2   . Če sta stran in dva vogala enega trikotnika, ki je poleg nje, enaka strani in dva vogala drugega trikotnika, ki je zraven nje, potem sta taka trikotnika enaka.

3    Če so tri strani enega trikotnika enake trem stranim drugega trikotnika, so takšni trikotniki enaki.

Pomembno:   ker sta v desnem trikotniku očitno enaka dva, za enakost dveh pravih trikotnikov  potrebna je enakost samo dveh elementov: dveh strani ali strani in akutnega kota.

Znaki podobnosti trikotnikov:

1 . Če sta obe strani enega trikotnika sorazmerni z obema stranema drugega trikotnika in koti, zaprti med tema stranema, sta enaki, potem so ti trikotniki podobni.

2   . Če so tri strani enega trikotnika sorazmerne s tremi stranmi drugega trikotnika, potem so ti trikotniki podobni.

3   . Če sta dva kota enega trikotnika enaka dvema kotoma drugega trikotnika, sta si ta trikotnika podobna.

Pomembno:   v podobnih trikotnikov so podobne stranice nasproti enakim kotom.

Menelausov izrek

Naj premica preseka trikotnik, kjer je točka njegovega presečišča s stranjo, točka njegovega presečišča s stranjo in točka njegovega presečišča s nadaljevanjem strani. Potem

Vaša zasebnost nam je pomembna. Zaradi tega smo razvili Pravilnik o zasebnosti, ki opisuje, kako uporabljamo in shranjujemo vaše podatke. Prosimo, preberite našo politiko zasebnosti in nas obvestite, če imate kakršna koli vprašanja.

Zbiranje in uporaba osebnih podatkov

Osebni podatki se nanašajo na podatke, ki jih je mogoče uporabiti za identifikacijo določene osebe ali za vzpostavitev stika z njim.

Od osebnih podatkov vas lahko prosimo, da kadar koli stopite v stik z nami.

Spodaj je nekaj primerov vrst osebnih podatkov, ki jih lahko zbiramo, in kako jih lahko uporabljamo.

Katere osebne podatke zbiramo:

• Ko na spletnem mestu pustite zahtevo, lahko zbiramo različne podatke, vključno z vašim imenom, telefonsko številko, e-poštnim naslovom itd.

Kako uporabljamo vaše osebne podatke:

• Osebni podatki, ki jih zbiramo, nam omogočajo, da vas kontaktiramo in poročamo o edinstvenih ponudbah, promocijah in drugih dogodkih ter prihajajočih dogodkih.
• Občasno bomo lahko uporabili vaše osebne podatke za pošiljanje pomembnih obvestil in sporočil.
• Osebne podatke lahko uporabimo tudi za notranje namene, na primer za izvajanje revizije, analize podatkov in različnih študij, da bi izboljšali storitve, ki jih ponujamo, in vam zagotovili priporočila v zvezi z našimi storitvami.
• Če sodelujete v žrebanju nagrad, tekmovanju ali podobnem promocijskem dogodku, bomo morda uporabili podatke, ki jih posredujete za upravljanje takšnih programov.

Razkritje tretjim osebam

Informacije, ki smo jih prejeli od vas, ne razkrivamo tretjim osebam.

Izjeme:

• Če je potrebno - v skladu z zakonom sodni sistem v sodnih postopkih in / ali na podlagi javnih preiskav ali poizvedovanj državnih organov na ozemlju Ruske federacije - razkrije vaše osebne podatke. Prav tako lahko razkrijemo podatke o vas, če ugotovimo, da je takšno razkritje potrebno ali primerno za varnostne namene, vzdrževanje javnega reda in miru ali druge socialno pomembne primere.
• V primeru reorganizacije, združitve ali prodaje lahko osebne podatke, ki jih zbiramo, prenesemo ustrezni tretji osebi, prejemniku.

Varstvo osebnih podatkov

Sprejemamo varnostne ukrepe - vključno z upravnimi, tehničnimi in fizičnimi - za zaščito vaših osebnih podatkov pred izgubo, tatvino in nepošteno uporabo ter pred nepooblaščenim dostopom, razkritjem, spreminjanjem in uničenjem.

Spoštujte svojo zasebnost na ravni podjetja

Da bi zagotovili, da so vaši osebni podatki varni, svojim zaposlenim sporočamo pravila zaupnosti in varnosti ter strogo spremljamo izvajanje ukrepov za zaupnost.

Danes bomo v lekciji nadaljevali s preučevanjem teme čudovitih točk trikotnika in se seznanili s izrekom o presečišču višin trikotnika.

V preteklih lekcijah smo dokazali, da se bisektorji trikotnika v eni točki sekajo, srednji pravokotniki na straneh trikotnika pa sekajo tudi v eni točki. Pred tem smo tudi dokazali, da se mediani trikotnika v eni točki sekajo. Izkaže se, da imajo višine trikotnika isto lastnost.

Izrek  Višine trikotnika (ali njihovega nadaljevanja) se v eni točki sekajo.

Dokaz.

Razmislite.

Torej je štirikotnik paralelogram.

Točka je sredina segmenta sredina pravokotno .

Točka je sredina segmenta sredina pravokotno .

Točka je sredina segmenta sredina pravokotno .

Torej, višine se sekajo v eni točki, na točki.

Kar je bilo potrebno dokazati.

V katerem koli trikotniku mediji in bisektorji pripadajo samemu trikotniku. Kaj ne moremo reči o višinah trikotnika. Tri višine trikotnika se vedno sekajo v eni točki. Pokliče se točka njihovega presečišča ortocenter trikotnika. V trikotniku z ostrim kotom in pravokotnikom višine pripadajo trikotniku. Njihovo presečišče - pravokotni center - v trikotniku z ostrim kotom je znotraj trikotnika, v pravokotnem trikotniku pod pravim kotom. Toda v nejasnem trikotniku je točka presečišča višin - ortocenter - zunaj trikotnika.

Razmislite o temno. Ima - neumno - višino. Dokažimo, da točka - osnova višine - ne pripada segmentu.

Dokaz.

Naj bo točka.

Kaj ne more biti.

Presečišče nejasnega trikotnika leži zunaj trikotnika.

Torej, z vsakim trikotnikom so povezane štiri točke: srednja točka presečišča presečišče bisektorjev, presečišče srednjih pravokotnikov na straneh trikotnika in presečišče višin (ali njihovih podaljškov).  Te štiri točke so poklicane čudovite trikotne točke.

Iz zgodovine čudovitih točk trikotnika. V četrti knjigi "Začelo"  Euclid reši težavo: "Vnesite krog v dani trikotnik." Iz rešitve izhaja, da v eni točki sekajo trije bisektorji notranjih kotov trikotnika  - središče vpisanega kroga.

Iz rešitve drugega evklidskega problema sledi, da pravokotne črte, obnovljene na straneh trikotnika v njihovih sredinahtudi v eni točki sekajo  - središče opisanega kroga. Začetki tega ne povejo se tri višine trikotnika sekajo v eni točkiimenovan ortocenter.

Četrta singularna točka trikotnika je presečišče medianov. Arhimed je dokazal, da je težišče (barcenter) trikotnika. Posebna pozornost je bila namenjena zgornjim štirim točkam, od 18. stoletja pa so jih poimenovali "čudovito"  ali "poseben"  točke trikotnika.

Preučevanje lastnosti trikotnika, povezanih s temi in drugimi točkami, je služilo kot začetek za nastanek nove veje osnovne matematike - "geometrija trikotnika"  ali "nova geometrija trikotnika", katerega izmed ustanoviteljev je bil Leonard Euler.

Ponovimo glavno:

V tej lekciji smo izvedeli, da se višine trikotnika (ali njihovih podaljškov) sekajo v eni točki. Ta točka se imenuje ortocenterin ona je čudovita točka trikotnika.

EA → ⋅ BC → + EB → ⋅ CA → + EC → ⋅ AB → \u003d 0 (\\ displaystyle (\\ overrightarrow (EA)) \\ cdot (\\ overrightarrow (BC)) + (\\ overrightarrow (EB)) \\ cdot (\\ (Če želite dokazati identiteto, uporabite formule

   AB → \u003d EB → - EA →, BC → \u003d EC → - EB →, CA → \u003d EA → - EC → (\\ displaystyle (\\ overrightarrow (AB)) \u003d (\\ overrightarrow (EB)) - (\\ overrightarrow (EA )), \\, (\\ overrightarrow (BC)) \u003d (\\ overrightarrow (EC)) - (\\ overrightarrow (EB)), \\, (\\ overrightarrow (CA)) \u003d (\\ overrightarrow (EA)) - (\\ overrightarrow (ES)))

{!LANG-da804231b2a9bc2a2337921444273c2a!}

Kot točko E bi morali vzeti presečišče dveh višin trikotnika.)

• Ortocenter  izogonalno do središča obkrožen krog .
• Ortocenter  leži na isti črti s središčem, sredino obkrožen krog  središče kroga devetih točk (glej Eulerjevo črto).
• Ortocenter  akutni kotni trikotnik je središče kroga, vpisanega v njegov pravokotni trikotnik.
• Središče trikotnika, ki ga ortocenter opisuje s točki na sredini strani danega trikotnika. Zadnji trikotnik se imenuje dodatni trikotnik glede na prvi trikotnik.
• Zadnjo lastnost lahko oblikujemo na naslednji način: Središče kroga, ki je opisan okoli trikotnika, služi ortocenter  dodatni trikotnik.
• Simetrične točke ortocenter  trikotnik glede na njegove stranice, leži na začrtanem krogu.
• Simetrične točke ortocenter  trikotnika glede na polovice strani ležijo tudi na opisanem krogu in sovpadajo s točkami, diametralno nasproti ustreznim vozliščem.
• Če Oh  je središče opisanega kroga ΔABC, torej    O H → \u003d O A → + O B → + O C → (\\ displaystyle (\\ overrightarrow (OH)) \u003d (\\ overrightarrow (OA)) + (\\ overrightarrow (OB)) + (\\ overrightarrow (OC))) ,
• Razdalja od vrha trikotnika do ortocentra je dvakrat večja kot razdalja od središča opisanega kroga do nasprotne strani.
• Iz katerega koli odseka ortocenter  do presečišča z obkroženim krogom ga vedno razdeli na dva dela Eulerjev krog. Ortocenter  za ta dva kroga obstaja center za homotetičnost.
• Hamiltonov izrek. Tri segmente črt, ki povezujejo ortocenter z vrhovi trikotnika z ostrim kotom, ga razdelijo na tri trikotnike, ki imajo enak Eulerjev krog (devettočkovni krog) kot prvotni trikotnik z ostrim kotom.
• Posledice Hamiltonovega teorema:
  • Trije odseki črt, ki povezujejo ortocenter z vrhovi ostrokotnega trikotnika, ga delijo na tri hamilton trikotnikz enakimi polmeri opisanih krogov.
  • Polmeri opisanih krogov treh hamiltonski trikotniki  enak polmeru kroga, opisanega v bližini prvotnega trikotnika z ostrim kotom.
• V trikotniku z ostrim kotom leži ortocenter znotraj trikotnika; v obtuse - zunaj trikotnika; v pravokotniku - na vrhu pravega kota.

Lastnosti višin enakokotnega trikotnika

• Če sta dve višini enaki v trikotniku, potem je trikotnik izosceles (Steiner-Lemusov izrek), tretja višina pa je srednja in bisektorija kota, iz katerega izstopa.
• Velja tudi obratno: v enakomernem trikotniku sta dve višini enaki, tretja višina pa je srednja in bisektorska.
• Enakostranski trikotnik ima vse tri višine enake.

Lastnosti višin trikotnika

• Razlogi  višine tvorijo tako imenovani orto-trikotnik, ki ima svoje lastnosti.
• Krog, ki je opisan okoli orto trikotnika, je Eulerjev krog. Na tem krogu ležijo tudi tri vmesne točke strani trikotnika in tri vmesne točke treh segmentov, ki povezujejo ortocenter z vrhovi trikotnika.
• Druga formulacija slednje lastnosti:
  • Eulerjev izrek za krog z devetimi točkami. Razlogi  od treh višine  poljuben trikotnik, sredina njegovih treh strani ( temelje njegovega notranjega  mediani) in sredina treh segmentov, ki povezujejo njegove konice z ortocentrom, vsi ležijo na istem krogu (na krog z devetimi točkami).
• Izrek. V katerem koli trikotniku je črta, ki povezuje razlogov  dva višine  trikotnik, odreže trikotnik, podoben temu.
• Izrek. V trikotniku črta, ki povezuje razlogov  dva višine  trikotniki, ki ležijo na dveh straneh, protiparalno  tretja oseba, s katero nima skupnih točk. Skozi njegova dva konca, pa tudi skozi dva vrhova tretje omenjene strani lahko vedno narišete krog.

Druge lastnosti višin trikotnika

Lastnosti najmanjših višin trikotnika

Najmanjša višina trikotnika ima veliko ekstremnih lastnosti. Na primer:

• Najmanjša pravokotna projekcija trikotnika na črte, ki ležijo v ravnini trikotnika, je dolžina enaka najmanjši od njegovih višin.
• Najmanjši ravni del v ravnini, skozi katero se lahko vleče upogljiva trikotna plošča, mora imeti dolžino, ki je enaka najmanjši višini te plošče.
• S stalnim premikom dveh točk po obodu trikotnika drug proti drugemu največja razdalja med njima med premikom od prvega srečanja na drugo ne more biti manjša od dolžine najmanjše višine trikotnika.
• Najmanjša višina trikotnika vedno prehaja znotraj tega trikotnika.

Glavni odnosi

•    h a \u003d b sin \u2061 γ \u003d c sin \u2061 β, (\\ displaystyle h_ (a) \u003d b \\ sin \\ gama \u003d c \\ sin \\ beta,)
•    h a \u003d 2 S a, (\\ zaslon h_ (a) \u003d (\\ frac (2S) (a)),)  kje    S (\\ prikazni slog S)  je območje trikotnika,    a (\\ displaystyle a)  - dolžina strani trikotnika, s katero se višina spušča.
• ha 2 \u003d 1 2 (b 2 + c 2 - 1 2 (a 2 + (b 2 - c 2) 2 a 2)) (\\ displaystyle h_ (a) ^ (2) \u003d (\\ frac (1) (2 )) (b ^ (2) + c ^ (2) - (\\ frac (1) (2)) (a ^ (2) + (\\ frac ((b ^ (2) -c ^ (2)) ^ (2)) (a ^ (2))))))
•    h a \u003d b c 2 R, (\\ prikazovalnik h_ (a) \u003d (\\ frac (bc) (2R)),)  kje    b c (\\ displaystyle bc)  - izdelek stranic,    R - (\\ zaslon R-)  polmer kroga
•    ha: hb: hc \u003d 1 a: 1 b: 1 c \u003d bc: ac: ab (\\ displaystyle h_ (a): h_ (b): h_ (c) \u003d (\\ frac (1) (a)) :( \\ frac (1) (b)): (\\ frac (1) (c)) \u003d bc: ac: ab)
•    1 ha + 1 hb + 1 hc \u003d 1 r (\\ displaystyle (\\ frac (1) (h_ (a))) + (\\ frac (1) (h_ (b))) + (\\ frac (1) (h_ (c))) \u003d (\\ frac (1) (r)))kje    r (\\ displaystyle r)  - polmer vpisanega kroga.
•    S \u003d 1 (1 ha + 1 hb + 1 hc) ⋅ (1 ha + 1 hb - 1 hc) ⋅ (1 ha + 1 hc - 1 hc) ⋅ (1 hb + 1 hc - 1 ha) (\\ displaystyle S \u003d (\\ frac (1) (\\ sqrt (((\\ frac (1) (h_ (a))) + (\\ frac (1) (h_ (b))) + (\\ frac (1) (h_ (c )))) (\\ cdot) ((\\ frac (1) (h_ (a))) + (\\ frac (1) (h_ (b))) - (\\ frac (1) (h_ (c))) ) (\\ cdot) ((\\ frac (1) (h_ (a))) + (\\ frac (1) (h_ (c))) - (\\ frac (1) (h_ (b)))) (\\ je območje trikotnika.kje    S (\\ prikazni slog S)   a \u003d 2 ha ⋅ (1 ha + 1 hb + 1 hc) ⋅ (1 ha + 1 hb - 1 hc) ⋅ (1 ha + 1 hc - 1 hb) ⋅ (1 hb + 1 hc - 1 ha) (\\ + (\\ frac (1) (h_ (c)))) (\\ cdot) ((\\ frac (1) (h_ (a))) + (\\ frac (1) (h_ (b))) - (\\ ) (h_ (b)))) (\\ cdot) ((\\ frac (1) (h_ (b))) + (\\ frac (1) (h_ (c))) - (\\ frac (1) (h_ (a)))))))))
•   - stran trikotnika, na katero se višina spusti,    a (\\ displaystyle a)   h a (\\ displaystyle h_ (a)) Višina enakotničnega trikotnika, spuščena na osnovo:.
•    h c \u003d 1 2 4 a 2 - c 2, (\\ displaystyle h_ (c) \u003d (\\ frac (1) (2)) (\\ sqrt (4a ^ (2) -c ^ (2))),)    c (\\ displaystyle c)

  kje   - osnova  - stran.    a (\\ displaystyle a) Teorem višine desnega trikotnika

Če je višina v pravem trikotniku

   A B C (\\ prikazni slog ABC)   dolgo   h (\\ prikazni slog h) izvlečen z vrha pravega kota deli hipotenuzo z dolžino  v segmente   - osnova   m (\\ prikazni slog m)   in   n (\\ prikazni slog n) ki ustrezajo nogam   b (\\ prikaz slog b) potem so naslednje enakosti.   n (\\ prikazni slog n)    a (\\ displaystyle a){!LANG-c00d69affff52836d4aa708de69b6aef!}

Za reševanje številnih geometrijskih problemov je potrebno najti višino dane figure. Te naloge so praktičnega pomena. Pri izvajanju gradbenih del določanje višine pomaga izračunati potrebno količino materialov, pa tudi določiti, kako natančno so narejena pobočja in odprtine. Pogosto za izdelavo vzorcev morate imeti predstavo o lastnostih

Veliko ljudi se kljub dobri oceni v šoli pri gradnji navadnih geometrijskih figur postavlja vprašanje, kako najti višino trikotnika ali paralelograma. In je najtežje. To je zato, ker je lahko trikotnik oster, tup, enake ali pravokoten. Vsak od njih ima svoja pravila gradnje in izračuna.

Kako najti višino trikotnika, v kateri so vsi koti ostri, grafično

Če so vsi koti trikotnika ostri (vsak kot v trikotniku je manjši od 90 stopinj), potem za iskanje višine naredite naslednje.

1. Glede na dane parametre konstruiramo trikotnik.
2. Uvedemo notacijo. A, B in C bodo točki figure. Koti, ki ustrezajo vsaki točki, so α, β, γ. Nasproti teh vogalov so a, b, c.
3. Višina je pravokotna, spuščena od vrha kota do nasprotne strani trikotnika. Za iskanje višin trikotnika konstruiramo pravokotnike: od vrha kota α do strani a, od vrha kota β do strani b in tako naprej.
4. Točka presečišča višine in strani a je označena s H1, višina h1 pa sama. Točka preseka višine in strani b bo H2, višina h2. Za stran c bo višina h3 in presečišče H3.

Višina v nejasnem trikotniku

Zdaj razmislite, kako najti višino trikotnika, če je ena (več kot 90 stopinj). V tem primeru bo višina, narisana iz trdega kota, znotraj trikotnika. Drugi dve višini bosta zunaj trikotnika.

Predpostavimo, da sta v našem trikotniku kota α in β ostra, kota γ pa naglušna. Potem je za izgradnjo višin, ki izhajajo iz kotov α in β, potrebno nadaljevati nasprotne strani trikotnika, da narišemo pravokotnike.

Kako najti višino enakomernega trikotnika

Takšna figura ima dve enaki strani in podlago, koti na dnu pa so tudi enaki drug drugemu. Ta enakost strani in kotov olajša gradnjo višin in njihov izračun.

Najprej narišite sam trikotnik. Strani b in c ter koti β, γ sta enaki.

Zdaj narišite višino od vrha kota α in ga označite s h1. Za to višino bo tako bisektor kot mediana.

Za temelje je mogoče narediti samo eno konstrukcijo. Na primer narišite sredino - segment, ki povezuje vrh trikotnika izosceles in nasprotno stran, osnovo, da poiščete višino in dolžino. In za izračun dolžine višine za drugi dve strani lahko zgradite samo eno višino. Tako je za grafično določitev višine trikotnika enakostile dovolj, da poiščemo dva od treh višin.

Kako najti višino pravega trikotnika

Mnogo lažje je določiti višine pravega trikotnika kot druge. To je zato, ker noge same tvorijo pravi kot, kar pomeni, da so višine.

Kot običajno običajno sestavimo pravokotno črto, ki povezuje vrh pravega kota in nasprotno stran. Zaradi tega je za trikotnik v tem primeru potrebna le ena konstrukcija.