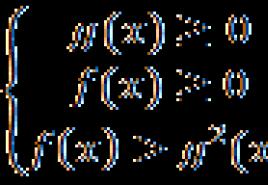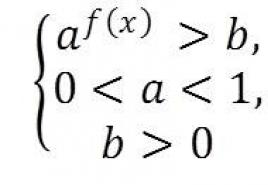Spletna rešitev linearne neenakosti s podrobno rešitvijo. Linearne neenakosti

Diagram na sliki 5:

In naslednji primer: Rešite neenakost 0,6 2x - 3< 0,36 .

Po shemi na sliki 5 dobimo
2x - 3> log 0,6 0,36,
2x - 3> 2,
2x> 5,
x> 2,5

Odgovor: (2,5; +∞) .

Razmislite o zadnji shemi za reševanje neenakosti oblike in f (x)< b , ob a> 0 in b<0 prikazano na sliki 6:

Na primer, rešimo neenakost:

Upoštevamo, da ne glede na to, katero število nadomestimo z x, je leva stran neenakosti vedno večja od nič, naš izraz pa manjši od -8, tj. in nič, potem ni rešitev.

Odgovor: brez rešitev.

Ko vemo, kako so rešene najpreprostejše eksponentne neenakosti, lahko nadaljujemo reševanje eksponentnih neenakosti.

Primer 1.

Poiščite največjo celoštevilčno vrednost x, ki izpolnjuje neenakost

Ker je 6 x večje od nič (za poljuben x imenovalec ne izgine), pomnožimo obe strani neenakosti s 6 x, dobimo:

440 - 2 6 2x> 8, torej
- 2 6 2x> 8 - 440,
- 2 6 2x> - 332,
6 2x< 216,
2x< 3,

x< 1,5. Наибольшее целое число из помежутка (–∞; 1,5) это число 1.

Odgovor: 1.

2. primer.

Rešite neenakost 2 2 x - 3 2 x + 2 ≤ 0

Označujemo 2 x skozi y, dobimo neenakost y 2 - 3y + 2 ≤ 0, rešujemo to kvadratno neenakost.

y 2 - 3y +2 = 0,
y 1 = 1 in y 2 = 2.

Veje parabole so usmerjene navzgor, narišimo graf:

Potem je rešitev neenakosti neenakost 1< у < 2, вернемся к нашей переменной х и получим неравенство 1< 2 х < 2, решая которое и найдем ответ 0 < x < 1.

Odgovor: (0; 1) .

3. primer... Rešite neenakost 5 x +1 - 3 x +2< 2·5 x – 2·3 x –1
Zbirajmo izraze z enakimi osnovami v enem delu neenakosti

5 x +1 - 2,5 x< 3 x +2 – 2·3 x –1

Izvlečemo 5 x na levi strani neenakosti in 3 х na desni strani neenakosti ter dobimo

5 x (5 - 2)< 3 х (9 – 2/3),
3 5 x< (25/3)·3 х

Obe strani neenakosti delimo z izrazom 3 3 x, znak neenakosti se ne spremeni, ker je 3 3 x pozitivno število, dobimo neenakost:

x< 2 (так как 5/3 > 1).

Odgovor: (–∞; 2) .

Če imate kakršna koli vprašanja o reševanju eksponentnih neenakosti ali če želite vaditi reševanje podobnih primerov, se prijavite na moje lekcije. Vaditeljica Valentina Galinevskaya.

spletnem mestu s popolnim ali delnim kopiranjem gradiva potrebna povezava do vira.

Reševanje neenakosti na spletu

Preden rešujemo neenakosti, moramo dobro razumeti, kako se enačbe rešujejo.

Ni pomembno, ali je neenakost stroga () ali nestroga (≤, ≥), prvi korak je rešiti enačbo in nadomestiti znak neenakosti z enakostjo (=).

Pojasnimo, kaj pomeni reševanje neenakosti?

Po preučitvi enačb v glavi učenca se razvije naslednja slika: najti morate take vrednosti spremenljivke, pri katerih obe strani enačbe prevzameta enake vrednosti. Z drugimi besedami, poiščite vse točke, kjer velja enakost. Tako je!

Ko govorimo o neenakostih, mislimo na iskanje intervalov (odsekov), na katerih neenakost velja. Če sta v neenakosti dve spremenljivki, potem rešitev ne bodo več intervali, temveč nekatera območja na ravnini. Ugani, kakšna bo rešitev neenakosti v treh spremenljivkah?

Kako se spoprijeti z neenakostmi?

Univerzalna metoda za reševanje neenakosti se šteje za metodo intervalov (aka metoda intervalov), ki je sestavljena iz določanja vseh intervalov, znotraj katerih bo navedena neenakost izpolnjena.

Ne da bi se spuščali v vrsto neenakosti, v tem primeru to ni bistvo, rešiti je treba ustrezno enačbo in določiti njene korenine, čemur sledi oznaka teh rešitev na osi števila.

Kako pravilno zapisati rešitev neenakosti?

Ko določite intervale rešitev neenakosti, morate pravilno zapisati rešitev. Obstaja pomemben odtenek - ali so meje intervalov vključene v raztopino?

Tu je vse preprosto. Če rešitev enačbe izpolnjuje GDV in neenakost ni stroga, je meja intervala vključena v rešitev neenakosti. V nasprotnem primeru ne.

Ob upoštevanju vsakega intervala je rešitev neenakosti lahko sam interval ali polinterval (kadar ena od njegovih meja izpolnjuje neenakost) ali segment - interval skupaj z njegovimi mejami.

Pomembna točka

Ne mislite, da so lahko samo intervali, pol intervali in odseki črt rešitev za neenakost. Ne, rešitev lahko vključuje posamezne točke.

Na primer, neenakost | x | ≤0 ima samo eno rešitev - to je točka 0.

In neenakost | x |

Čemu služi kalkulator neenakosti?

Kalkulator neenakosti daje pravilen končni odgovor. V tem primeru je v večini primerov podana slika številčne osi ali ravnine. Videti je, ali so meje intervalov vključene v raztopino ali ne - točke so prikazane kot napolnjene ali preluknjane.

Zahvaljujoč spletnemu kalkulatorju neenakosti lahko preverite, ali ste pravilno našli korenine enačbe, jih označili na številčni osi in preverili pogoj neenakosti na intervalih (in mejah)?

Če se vaš odgovor razlikuje od odgovora kalkulatorja, morate vsekakor še enkrat preveriti svojo odločitev in ugotoviti napako.

Neenakost je številčno razmerje, ki ponazarja velikost števil med seboj. Neenakosti se pogosto uporabljajo pri iskanju količin v uporabnih znanostih. Naš kalkulator vam bo pomagal pri soočanju s tako težko temo, kot je reševanje linearnih neenakosti.

Kaj je neenakost

Neenaki odnosi v resničnem življenju se nanašajo na nenehno primerjavo različnih predmetov: višje ali nižje, dlje ali bližje, težje ali lažje. Intuitivno ali vizualno lahko razumemo, da je en predmet večji, višji ali težji od drugega, v resnici pa vedno govorimo o primerjavi števil, ki označujejo ustrezne vrednosti. Predmete lahko primerjate po katerem koli kriteriju, v vsakem primeru pa lahko sestavimo številčno neenakost.

Če so neznane količine pod določenimi pogoji enake, potem za njihovo numerično določitev sestavimo enačbo. V nasprotnem primeru lahko namesto znaka "enako" označimo katero koli drugo razmerje med temi vrednostmi. Dve številki ali matematični predmeti sta lahko večji od ">", manjši od "<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.

Znake neenakosti v sodobni obliki je izumil britanski matematik Thomas Garriot, ki je leta 1631 izdal knjigo o neenakih razmerjih. Znaki večji od ">" in manj "<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.

Reševanje neenakosti

Neenakosti, tako kot enačbe, so različnih vrst. Linearna, kvadratna, logaritemska ali eksponentna neenaka razmerja se ločijo z različnimi metodami. Vendar je treba ne glede na metodo vsako neenakost najprej zmanjšati na standardno obliko. Za to se uporabljajo enake transformacije, ki so enake spremembam enakosti.

Enake transformacije neenakosti

Takšne transformacije izrazov so zelo podobne duhu enačb, vendar imajo nianse, ki jih je treba upoštevati pri ločevanju neenakosti.

Prva enaka transformacija je enaka analogni operaciji z enakostmi. Na obe strani neenakega razmerja lahko dodate ali odštejete isto število ali izraz z neznanim x, medtem ko bo znak neenakosti ostal enak. Najpogosteje se ta metoda uporablja v poenostavljeni obliki kot prenos izrazov izraza skozi znak neenakosti s spremembo predznaka števila v nasprotno. To pomeni spremembo predznaka samega izraza, to pomeni, da se + R ob prenosu skozi kateri koli znak neenakosti spremeni v - R in obratno.

Druga preobrazba ima dve točki:

1. Obe strani neenakega razmerja je dovoljeno pomnožiti ali deliti z enakim pozitivnim številom. V tem primeru se sam znak neenakosti ne bo spremenil.
2. Obe strani neenakosti je dovoljeno deliti ali pomnožiti z enakim negativnim številom. Znak same neenakosti bo obrnjen.

Druga enaka transformacija neenakosti ima resne razlike s spreminjanjem enačb. Prvič, pri množenju / deljenju z negativnim številom je znak neenakega izraza vedno obrnjen. Drugič, delitev ali množenje delov relacije je dovoljeno samo s številom in ne z nobenim izrazom, ki vsebuje neznano. Dejstvo je, da ne moremo zagotovo vedeti, ali se za neznanim skriva število, večje ali manjše od nič, zato se druga enaka transformacija uporablja za neenakosti izključno s števili. Poglejmo ta pravila s primeri.

Primeri sproščanja neenakosti

Naloge algebre vsebujejo najrazličnejše naloge neenakosti. Dajmo nam izraz:

6x - 3 (4x + 1)> 6.

Najprej odpremo oklepaje in vse neznanke premaknemo v levo, vse številke pa v desno.

6x - 12x> 6 + 3

Obe strani izraza moramo razdeliti z −6, tako da se bo, ko bomo našli neznanega x, znak neenakosti spremenil v nasprotno.

Pri reševanju te neenakosti smo uporabili obe enaki transformaciji: vsa števila prenesli desno od znaka in obe strani razmerja razdelili na negativno število.

Naš program je kalkulator za reševanje numeričnih neenakosti, ki ne vsebujejo neznank. Program vsebuje naslednje izreke za razmerja treh števil:

• če< B то A–C< B–C;
• če je A> B, potem A - C> B - C.

Namesto da bi odštevali člane A - C, lahko podate katero koli aritmetično operacijo: seštevanje, množenje ali deljenje. Tako bo kalkulator samodejno prikazal neenakosti vsot, razlik, zmnožkov ali ulomkov.

Zaključek

V resničnem življenju so neenakosti tako pogoste kot enačbe. Seveda v vsakdanjem življenju znanje o reševanju neenakosti morda ne bo potrebno. Vendar se neenakosti in njihovi sistemi pogosto uporabljajo v uporabnih znanostih. Na primer, različne študije problemov svetovnega gospodarstva so omejene na sestavljanje in sproščanje sistemov linearnih ali kvadratnih neenakosti, nekatera neenaka razmerja pa služijo kot nedvoumen način dokazovanja obstoja določenih predmetov. Uporabite naše programe za reševanje linearnih neenakosti ali preverite svoje izračune.

Metoda razmika- preprost način reševanja delno-racionalnih neenakosti. To je ime neenakosti, ki vsebujejo racionalne (ali delno racionalne) izraze, ki so odvisni od spremenljivke.

1. Razmislite na primer o takšni neenakosti

Intervalska metoda vam omogoča, da jo rešite v nekaj minutah.

Na levi strani te neenakosti je delna racionalna funkcija. Racionalno, ker ne vsebuje korenin, sinusov, logaritmov - samo racionalni izrazi. Na desni je nič.

Intervalska metoda temelji na naslednji lastnosti delne racionalne funkcije.

Delna racionalna funkcija lahko spremeni znak samo na tistih točkah, na katerih je enaka nič ali ne obstaja.

Spomnimo se, kako se kvadratni trinom razgradi na faktorje, to je izraz oblike.

Kje in so korenine kvadratne enačbe.

Narišite os in postavite točke, na katerih števec in imenovalec izgineta.

Zero imenovalca in so preluknjane točke, saj na teh točkah funkcija na levi strani neenakosti ni definirana (ne morete deliti z ničlo). Številčne ničle in - so zapolnjene, saj neenakost ni stroga. Za in je naša neenakost zadovoljena, saj sta obe njeni strani enaki nič.

Te točke delijo os na intervale.

Določimo znak delno-racionalne funkcije na levi strani naše neenakosti na vsakem od teh intervalov. Spomnimo se, da lahko delna racionalna funkcija spremeni znak samo na tistih točkah, na katerih je enaka nič ali ne obstaja. To pomeni, da bo v vsakem intervalu med točkami, kjer števec ali imenovalec izgine, znak izraza na levi strani neenakosti konstanten - bodisi "plus" ali "minus".

In zato za določitev predznaka funkcije v vsakem takem intervalu vzamemo katero koli točko, ki pripada temu intervalu. Tista, ki je za nas primerna.
... Vzemimo na primer in preverimo znak izraza na levi strani neenakosti. Vsak od "oklepajev" je negativen. Na levi strani je znak.

Naslednji razpon :. Preverimo znak za. Ugotovimo, da je leva stran spremenila znak v.

Vzemimo. Kadar je izraz pozitiven, je torej pozitiven v celotnem intervalu od do.

Leva stran neenakosti je namreč negativna.

Končno, class = "tex" alt = "(! LANG: x> 7"> . Подставим и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .!}

Ugotovili smo, v kakšnih intervalih je izraz pozitiven. Odgovor je treba še zapisati:

Odgovor :.

Upoštevajte, da se znaki v presledkih izmenjujejo. To se je zgodilo, ker pri prehodu skozi vsako točko je točno eden od linearnih faktorjev spremenil znak, ostali pa so ga ohranili nespremenjenega.

Vidimo, da je metoda razmika zelo preprosta. Za rešitev delno-racionalne neenakosti z intervalno metodo jo privedemo v obliko:

Ali class = "tex" alt = "(! LANG: \ genfrac () () () (0) (\ displaystyle P \ left (x \ right)) (\ displaystyle Q \ left (x \ right))> 0"> !}, ali ali.

(na levi - delna racionalna funkcija, na desni - nič).

Nato - na številski črti označimo točke, na katerih števec ali imenovalec izgine.
Te točke delijo celotno številsko premico na intervale, na katerih vsaka delna racionalna funkcija ohrani svoj znak.
V vsakem intervalu je treba šele ugotoviti njegov znak.
To naredimo tako, da preverimo znak izraza na kateri koli točki, ki pripada danemu intervalu. Po tem zapišemo odgovor. To je vse.

Toda postavlja se vprašanje: ali se znaki vedno izmenjujejo? Ne ne vedno! Paziti je treba, da napisov ne postavljate mehanično in nepremišljeno.

2. Poglejmo še eno neenakost.

Razred = "tex" alt = "(! LANG: \ genfrac () () () (0) (\ displaystyle \ left (x-2 \ right) ^ 2) (\ displaystyle \ left (x-1 \ right) \ levo (x-3 \ desno))> 0"> !}

Ponovno postavite točke na os. Pike in so izsekane, ker so ničli imenovalca. Bistvo je tudi preluknjano, saj je neenakost stroga.

Če je števec pozitiven, sta oba faktorja v imenovalcu negativna. To je enostavno preveriti tako, da na primer vzamete katero koli številko iz danega intervala. Na levi strani je znak:

Ko je števec pozitiven; prvi faktor v imenovalcu je pozitiven, drugi faktor pa negativen. Na levi strani je znak:

Stanje je enako! Števec je pozitiven, prvi faktor v imenovalcu je pozitiven, drugi je negativen. Na levi strani je znak:

Na koncu še z class = "tex" alt = "(! LANG: x> 3"> все множители положительны, и левая часть имеет знак :!}

Odgovor :.

Zakaj je bilo menjavanje znakov prekinjeno? Ker pri prehodu skozi točko je dejavnik, "odgovoren" zanjo ni spremenil znaka... Posledično tudi celotna leva stran naše neenakosti ni spremenila svojega predznaka.

Izhod: če je linearni faktor v enakomerni moči (na primer v kvadratu), se pri prehodu skozi točko znak izraza na levi strani ne spremeni... V primeru nenamerne stopnje se znak seveda spremeni.

3. Poglejmo si bolj zapleten primer. Od prejšnje se razlikuje po tem, da neenakost ni stroga:

Leva stran je enaka prejšnji nalogi. Slika znakov bo enaka:

Mogoče bo odgovor enak? Ne! Dodana je rešitev To je zato, ker sta levi in ​​desni strani neenakosti enaki nič - torej je ta točka rešitev.

Odgovor :.

Pri problemu za izpit iz matematike se pogosto srečujemo s to situacijo. Tu se kandidati ujamejo v past in izgubijo točke. Bodi previden!

4. Kaj pa, če števca ali imenovalca ni mogoče linearizirati? Razmislite o tej neenakosti:

Kvadratnega trinoma ni mogoče razstaviti na faktor: diskriminant je negativen, korenin ni. Ampak to je dobro! To pomeni, da je znak izraza za vse enak, natančneje pozitiven. Več o tem lahko preberete v članku o lastnostih kvadratne funkcije.

In zdaj lahko obe strani naše neenakosti razdelimo na vrednost, ki je pozitivna za vse. Prišli smo do enakovredne neenakosti:

Kar je enostavno rešiti z metodo intervalov.

Upoštevajte - obe strani neenakosti smo razdelili na znesek, za katerega smo zagotovo vedeli, da je pozitiven. Seveda v splošnem primeru ni vredno množiti ali deliti neenakosti s spremenljivko, katere predznak ni znan.

5 ... Razmislite o drugi neenakosti, ki je na videz povsem preprosta:

Želim ga samo pomnožiti z. Toda že smo pametni in tega ne bomo storili. Navsezadnje je lahko pozitiven in negativen. In vemo, da če se obe strani neenakosti pomnožijo z negativno vrednostjo, se znak neenakosti spremeni.

Naredili bomo drugače - vse bomo zbrali v enem delu in pripeljali do skupnega imenovalca. Zero bo ostalo na desni strani:

Razred = "tex" alt = "(! LANG: \ genfrac () () () (0) (\ displaystyle x-2) (\ displaystyle x)> 0"> !}

In po tem - se bomo prijavili intervalna metoda.

V članku bomo razmislili rešitev neenakosti... Na dostopen način vam bomo povedali o kako zgraditi rešitev za neenakosti, z jasnimi primeri!

Preden na primerih razmislimo o rešitvi neenakosti, razumimo osnovne pojme.

Splošne informacije o neenakostih

Neenakost se imenuje izraz, v katerem so funkcije povezane z relacijskimi znaki> ,. Neenakosti so tako številčne kot abecedne.
Neenakosti z dvema znakoma zveze se imenujejo dvojne, s tremi - trojne itd. Na primer:
a (x)> b (x),
a (x) a (x) b (x),
a (x) b (x).
a (x) neenakosti, ki vsebujejo znak> ali pa niso stroge.
Reševanje neenakosti je katera koli vrednost spremembe, pri kateri je ta neenakost resnična.
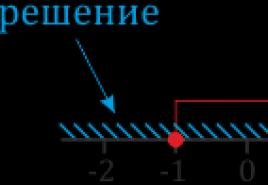
"Rešite neenakost"pomeni, da je treba najti številne njegove rešitve. Obstajajo različne metode za reševanje neenakosti... Za rešitve neenakosti uporabite številčno črto, ki je neskončna. Na primer rešitev neenakosti x> 3 je interval od 3 do +, številka 3 pa ni vključena v ta interval, zato je točka na ravni črti označena s praznim krogom, saj neenakost je stroga.
+
Odgovor bo: x (3; +).
Vrednost x = 3 ni vključena v nabor rešitev, zato je oklepaj okrogla. Znak neskončnosti je vedno obdan z oklepaji. Znak pomeni "pripadnost".
Poglejmo, kako rešiti neenakosti na drugem podpisanem primeru:
x 2
-+
Vrednost x = 2 je vključena v nabor rešitev, zato je oklepaj kvadratni, točka na premici pa označena z zapolnjenim krogom.
Odgovor bo: x)