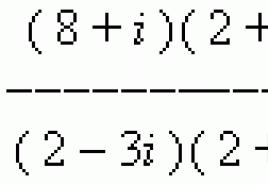Teorija kompleksnih števil in primeri. Kompleksne številke
Kompleksne številke
Imaginarno in kompleksna števila. Abscisa in ordinata
kompleksno število. Konjugirajte kompleksna števila.
Operacije s kompleksnimi števili. Geometrijsko
predstavitev kompleksnih števil. kompleksna ravnina.
Modul in argument kompleksnega števila. trigonometrično
kompleksna oblika števila. Operacije s kompleksom
števila v trigonometrični obliki. Moivre formula.
Osnovne informacije o imaginarno in kompleksna števila so podane v razdelku "Namišljena in kompleksna števila". Potreba po teh številkah novega tipa se je pojavila pri reševanju kvadratnih enačb za primer
D< 0 (здесь Dje diskriminanta kvadratne enačbe). Te številke dolgo niso našle fizične uporabe, zato so jih poimenovali »namišljena« števila. Vendar pa se zdaj zelo pogosto uporabljajo na različnih področjih fizike.in tehnologija: elektrotehnika, hidro- in aerodinamika, teorija elastičnosti itd.
Kompleksne številke so zapisani kot:a+bi. tukaj a in b – realne številke , a jaz – imaginarna enota. e. jaz 2 = –1. Številka a poklical abscisa, a b - ordinatakompleksno številoa + b .Dve kompleksni številkia+bi in a-bi poklical konjugirati kompleksna števila.
Glavni dogovori:
1. Realno število
alahko zapišemo tudi v oblikikompleksno število:a + 0 jaz oz a - 0 jaz. Na primer, vnosi 5 + 0jaz in 5 - 0 jazpomeni isto številko 5 .2. Kompleksno število 0 + bipoklical čisto namišljeno številko. Snemanjebipomeni isto kot 0 + bi.
3. Dve kompleksni številia+bi inc + dise štejejo za enake, čea = c in b = d. sicer kompleksna števila niso enaka.
Dodatek. Vsota kompleksnih števila+bi in c + dise imenuje kompleksno število (a+c ) + (b+d ) jaz .V to smer, ko je dodano kompleksna števila, njihove abscise in ordinate se dodajo ločeno.
Ta definicija sledi pravilom za ravnanje z navadnimi polinomi.
Odštevanje. Razlika med dvema kompleksnima številkamaa+bi(zmanjšano) in c + di(odšteto) se imenuje kompleksno število (a-c ) + (b-d ) jaz .
V to smer, pri odštevanju dveh kompleksnih števil se njune abscise in ordinate odštejejo ločeno.
Množenje. Produkt kompleksnih števila+bi in c + di se imenuje kompleksno število.
(ac-bd ) + (ad+bc ) jaz .Ta opredelitev izhaja iz dveh zahtev:
1) številke a+bi in c + dimnožiti kot algebraično binomi,
2) številka jazima glavno lastnost:jaz 2 = – 1.
PRIMER ( a + bi )(a-bi) = a 2 +b 2 . zato delo
dve konjugirani kompleksni števili je enako realnemu
pozitivno število.
divizije. Delite kompleksno številoa+bi (deljivo) na drugoc + di(delilnik) - pomeni najti tretjo številkoe + fi(klepet), ki se pomnoži z delilnikomc + di, kar ima za posledico dividendea + b .
Če delilec ni nič, je deljenje vedno možno.
PRIMER Najdi (8+jaz ) : (2 – 3 jaz) .
Rešitev Prepišimo to razmerje kot ulomek:
Njegov števec in imenovalec pomnožimo z 2 + 3jaz
IN po izvedbi vseh transformacij dobimo:

Geometrijski prikaz kompleksnih števil. Realna števila so predstavljena s točkami na številski premici:
Tukaj je bistvo Apomeni število -3, pikaB je številka 2 in O- nič. Nasprotno pa so kompleksna števila predstavljena s točkami na koordinatni ravnini. Za to izberemo pravokotne (kartezijanske) koordinate z enakim merilom na obeh oseh. Nato kompleksno številoa+bi bo predstavljena s piko P z absciso a in ordinato b (glej sliko). Ta koordinatni sistem se imenuje kompleksna ravnina .

modul kompleksno število imenujemo dolžina vektorjaOP, ki prikazuje kompleksno število na koordinati ( celovito) letalo. Kompleksni številski modula+bi označeno z | a+bi| ali pismo r
Učni načrt.
1. Organizacijski trenutek.
2. Predstavitev gradiva.
3. Domača naloga.
4. Povzetek lekcije.
Med poukom
I. Organizacijski trenutek.
II. Predstavitev gradiva.
Motivacija.
Razširitev množice realnih števil je v tem, da se realnim številkam dodajo nova števila (namišljena). Uvedba teh številk je povezana z nemožnostjo v množici realnih števil izvleči koren iz negativnega števila.
Uvedba pojma kompleksno število.
Namišljena števila, s katerimi dopolnjujemo realna števila, so zapisana kot bi, kje jaz je imaginarna enota in i 2 = - 1.
Na podlagi tega dobimo naslednjo definicijo kompleksnega števila.
Opredelitev. Kompleksno število je izraz oblike a+bi, kje a in b so resnične številke. V tem primeru so izpolnjeni naslednji pogoji:
a) Dve kompleksni števili a 1 + b 1 i in a 2 + b 2 i enako, če in samo če a 1 = a 2, b1=b2.
b) Seštevanje kompleksnih števil je določeno s pravilom:
(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.
c) Množenje kompleksnih števil je določeno s pravilom:
(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.
Algebraična oblika kompleksnega števila.
Zapis kompleksnega števila v obrazec a+bi se imenuje algebraična oblika kompleksnega števila, kjer a- pravi del bi je imaginarni del in b je realna številka.
Kompleksno število a+bi se šteje za enako nič, če sta njen resnični in imaginarni del enaka nič: a=b=0
Kompleksno število a+bi pri b = 0šteje za pravo število a: a + 0i = a.
Kompleksno število a+bi pri a = 0 se imenuje čisto imaginarna in je označena bi: 0 + bi = bi.
Dve kompleksni številki z = a + bi in = a – bi, ki se razlikujejo le v predznaku imaginarnega dela, se imenujejo konjugati.
Dejanja nad kompleksnimi števili v algebraični obliki.
Naslednje operacije se lahko izvajajo nad kompleksnimi števili v algebraični obliki.
1) Dodatek.
Opredelitev. Vsota kompleksnih števil z 1 = a 1 + b 1 i in z 2 = a 2 + b 2 i imenovano kompleksno število z, katerega realni del je enak vsoti realnih delov z1 in z2, imaginarni del pa je vsota namišljenih delov števil z1 in z2, to je z = (a 1 + a 2) + (b 1 + b 2)i.
Številke z1 in z2 se imenujejo izrazi.
Seštevanje kompleksnih števil ima naslednje lastnosti:
1º. komutativnost: z1 + z2 = z2 + z1.
2º. Asociativnost: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).
3º. Kompleksno število -a -bi se imenuje nasprotje kompleksnega števila z = a + bi. Kompleksno število nasproti kompleksnega števila z, označeno -z. Vsota kompleksnih števil z in -z enako nič: z + (-z) = 0
Primer 1: Dodaj (3 - i) + (-1 + 2i).
(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
2) Odštevanje.
Opredelitev. Odštejte od kompleksnega števila z1 kompleksno število z2 z, kaj z + z 2 = z 1.
Izrek. Razlika kompleksnih števil obstaja in je poleg tega edinstvena.
Primer 2: Odštej (4 - 2i) - (-3 + 2i).
(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 - 4i.
3) Množenje.
Opredelitev. Produkt kompleksnih števil z 1 =a 1 +b 1 i in z 2 \u003d a 2 + b 2 i imenovano kompleksno število z, opredeljeno z enakostjo: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.
Številke z1 in z2 imenujemo dejavniki.
Množenje kompleksnih števil ima naslednje lastnosti:
1º. komutativnost: z 1 z 2 = z 2 z 1.
2º. Asociativnost: (z 1 z 2)z 3 = z 1 (z 2 z 3)
3º. Distributivnost množenja glede na seštevanje:
(z 1 + z 2) z 3 \u003d z 1 z 3 + z 2 z 3.
4º. z \u003d (a + bi) (a - bi) \u003d a 2 + b 2 je realna številka.
V praksi se množenje kompleksnih števil izvaja po pravilu, da se seštevek pomnoži z vsoto in loči realni in namišljeni del.
V naslednjem primeru razmislite o množenju kompleksnih števil na dva načina: s pravilom in z množenjem vsote z vsoto.
Primer 3: Pomnožite (2 + 3i) (5 – 7i).
1 način. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15 )i = 31 + i.
2 način. (2 + 3i) (5 - 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.
4) Oddelek.
Opredelitev. Delite kompleksno število z1 na kompleksno število z2, pomeni najti tako kompleksno število z, kaj z z 2 = z 1.
Izrek. Kvocient kompleksnih števil obstaja in je edinstven, če z2 ≠ 0 + 0i.
V praksi najdemo količnik kompleksnih števil tako, da števec in imenovalec pomnožimo s konjugatom imenovalca.
Pustiti z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, potem



 .
.
V naslednjem primeru izvedemo deljenje s formulo in pravilo množenja s konjugatom imenovalca.
Primer 4. Poiščite količnik  .
.
5) Dvig na pozitivno celo število.
a) Moči imaginarne enote.
Izkoriščanje enakosti i 2 \u003d -1, je enostavno definirati katero koli pozitivno celo število imaginarne enote. Imamo:
i 3 \u003d i 2 i = -i,
i 4 \u003d i 2 i 2 \u003d 1
i 5 \u003d i 4 i \u003d i,
i 6 \u003d i 4 i 2 \u003d -1,
i 7 \u003d i 5 i 2 \u003d -i,
i 8 = i 6 i 2 = 1 itd.
To kaže, da vrednosti stopinj i n, kje n- pozitivno celo število, ki se občasno ponavlja, ko se indikator poveča za 4 .
Zato za dvig števila jaz na pozitivno celo število, eksponent delimo z 4 in pokonci jaz na potenco, katere eksponent je preostanek deljenja.
Primer 5 Izračunaj: (i 36 + i 17) i 23.
i 36 = (i 4) 9 = 1 9 = 1,
i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 i = i.
i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 i 3 = - i.
(i 36 + i 17) i 23 \u003d (1 + i) (- i) \u003d - i + 1 \u003d 1 - i.
b) Dvig kompleksnega števila na pozitivno celo število poteka po pravilu dviga binoma na ustrezno potenco, saj gre za poseben primer množenja enakih kompleksnih faktorjev.
Primer 6 Izračunaj: (4 + 2i) 3
(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.
Kompleksna števila so minimalna razširitev množice nam znanih realnih števil. Njihova temeljna razlika je v tem, da se pojavi element, ki na kvadrat daje -1, t.j. i, ali.
Vsako kompleksno število ima dva dela: resnične in namišljene:
Tako je jasno, da množica realnih števil sovpada z množico kompleksnih števil z nič namišljenim delom.
Najbolj priljubljen model za nabor kompleksnih številk je navadna ravnina. Prva koordinata vsake točke bo njen dejanski del, druga pa namišljena. Potem bodo vloga samih kompleksnih številk vektorji z začetkom v točki (0,0).
Operacije nad kompleksnimi števili.
Dejansko je, če upoštevamo model množice kompleksnih števil, intuitivno jasno, da se seštevanje (odštevanje) in množenje dveh kompleksnih števil izvajata na enak način kot ustrezne operacije na vektorjih. Poleg tega mislimo na navzkrižni produkt vektorjev, ker je rezultat te operacije spet vektor.
1.1 Dodatek.
(Kot vidite, ta operacija natančno ustreza )
1.2 Odštevanje, se podobno izvaja po naslednjem pravilu:
2. Množenje.

3. Oddelek.
Opredeljen je preprosto kot inverzna operacija množenja.

trigonometrična oblika.
Modul kompleksnega števila z je naslednja količina:
 ,
,
očitno je, da je to spet preprosto modul (dolžina) vektorja (a,b).
Najpogosteje je modul kompleksnega števila označen kot ρ.
Izkazalo se je, da
z = ρ(cosφ+isinφ).

Iz trigonometrične oblike zapisovanja kompleksnega števila neposredno sledi naslednje. formule :
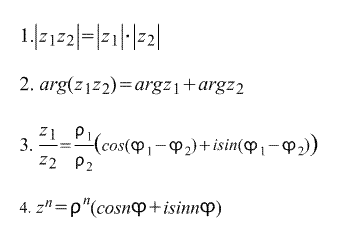
Zadnja formula se imenuje Formula De Moivre. Formula je izpeljana neposredno iz nje. n-ti koren kompleksnega števila:

torej obstaja n n-tih korenov kompleksnega števila z.