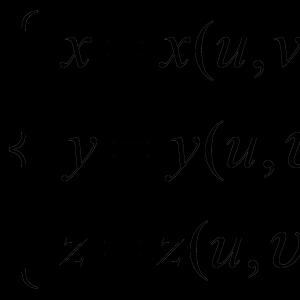Ecuația unei drepte în segmente are forma. Ecuația unei linii drepte în segmente - descriere, exemple, rezolvare de probleme

Continuăm să studiem secțiunea „Ecuația unei drepte pe un plan” și în acest articol vom analiza subiectul „Ecuația unei drepte în segmente”. Vom lua în considerare succesiv forma ecuației unei drepte în segmente, construcția unei drepte, care este dată de această ecuație, trecerea de la ecuația generală a unei drepte la ecuația unei drepte în segmente. Toate acestea vor fi însoțite de exemple și analize de rezolvare a problemelor.

Fie un sistem de coordonate dreptunghiular O x y situat pe plan.

O linie dreaptă pe un plan în sistemul de coordonate carteziene O xy este dată de o ecuație de forma xa + yb = 1 , unde a și b sunt numere reale diferite de zero ale căror valori sunt egale cu lungimile segmentelor tăiate de linia dreaptă pe axele O x și O y . Lungimile segmentelor sunt considerate de la originea coordonatelor.

După cum știm, coordonatele oricăruia dintre punctele aparținând unei drepte date de ecuația unei drepte satisfac ecuația acestei drepte. Punctele a , 0 și 0 , b aparțin acestei drepte, deoarece a a + 0 b = 1 ⇔ 1 ≡ 1 și 0 a + b b = 1 ⇔ 1 ≡ 1 . Punctele a , 0 și b , 0 sunt situate pe axele de coordonate O x și O y și sunt îndepărtate de la origine prin unități a și b. Direcția în care doriți să amânați lungimea segmentului este determinată de semnul care vine înaintea numerelor a și b. Semnul „-” înseamnă că lungimea segmentului trebuie trasată în direcția negativă a axei de coordonate.

Să explicăm toate cele de mai sus plasând liniile relativ la un sistem de coordonate carteziene fix O x y într-un desen schematic. Ecuația unei drepte în segmentele x a + y b = 1 este folosită pentru a construi o dreaptă în sistemul de coordonate carteziene O x y . Pentru a face acest lucru, trebuie să marchem punctele a, 0 și b, 0 pe axe și apoi să conectăm aceste puncte cu o linie folosind o riglă.

Desenul prezintă cazuri în care numerele a și b au semne diferite și, prin urmare, lungimile segmentelor sunt reprezentate în direcții diferite ale axelor de coordonate.

Luați în considerare un exemplu.

Exemplul 1

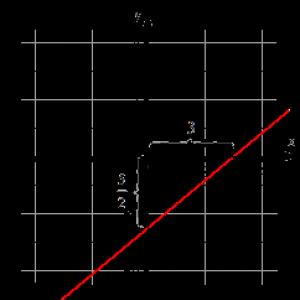
Linia dreaptă este dată de ecuația dreptei în segmente de forma x 3 + y - 5 2 = 1 . Este necesar să se construiască această dreaptă pe planul din sistemul de coordonate carteziene O x y .

Soluţie

Folosind ecuația unei drepte în segmente, determinăm punctele prin care trece linia dreaptă. Este 3 0 0 - 5 2 . Să le marchem și să tragem o linie.

Reducerea ecuației generale a unei drepte la ecuația unei drepte în segmente

Trecerea de la ecuația dată a unei linii drepte la ecuația unei drepte în segmente ne face mai ușor să rezolvăm diverse probleme. Având ecuația generală completă a unei drepte, putem obține ecuația unei drepte în segmente.

Ecuația generală completă a unei drepte în plan are forma A x + B y + C = 0, unde A, B și C nu sunt egale cu zero. Transferăm numărul C în partea dreaptă a egalității, împărțim ambele părți ale egalității rezultate la - C. În același timp, trimitem coeficienții pentru x și y la numitori:

A x + B y + C = 0 ⇔ A x + B y = - C ⇔ ⇔ A - C x + B - C y = 1 ⇔ x - C A + y - C B = 1

Pentru a implementa ultima tranziție, am folosit egalitatea p q = 1 q p , p ≠ 0 , q ≠ 0 .

Ca urmare, am făcut trecerea de la ecuația generală a dreptei A x + B y + C = 0 la ecuația dreptei din segmentele xa + yb = 1 , unde a = - CA , b = - CB.

Să luăm în considerare următorul exemplu.

Exemplul 2

Să facem trecerea la ecuația unei drepte în segmente, având ecuația generală a unei drepte x - 7 y + 1 2 = 0 .

Soluţie

Transferăm o secundă în partea dreaptă a egalității x - 7 y + 1 2 = 0 ⇔ x - 7 y = - 1 2 .

Împărțiți ambele părți ale ecuației la - 1 2: x - 7 y = - 1 2 ⇔ 1 - 1 2 x - 7 - 1 2 y = 1 .

Să transformăm egalitatea rezultată în forma dorită: 1 - 1 2 x - 7 - 1 2 y = 1 ⇔ x - 1 2 + y 1 14 = 1 .

Am obținut ecuația unei drepte în segmente.

Răspuns: x - 1 2 + y 1 14 = 1

În cazurile în care o dreaptă este dată de o ecuație canonică sau parametrică a unei drepte pe un plan, atunci trecem mai întâi la ecuația generală a unei drepte și apoi la ecuația unei drepte în segmente.

Trecerea de la ecuația unei linii drepte în segmente și ecuația generală a unei linii drepte este simplă: transferăm unitatea din partea dreaptă a ecuației unei linii drepte în segmente de forma xa + yb \u003d 1 la stânga partea cu semnul opus, selectăm coeficienții în fața necunoscutelor x și y.

x a + y b = 1 ⇔ x a + y b - 1 = 0 ⇔ 1 a x + 1 b y - 1 = 0

Obținem ecuația generală a unei drepte, din care putem trece la orice altă formă a ecuației unei drepte într-un plan. Am analizat în detaliu procesul de tranziție în subiectul „Reducerea ecuației generale a unei linii drepte la alte tipuri de ecuații a unei linii drepte”.

Exemplul 3

Ecuația unei drepte în segmente are forma x 2 3 + y - 12 = 1. Este necesar să scrieți ecuația generală a unei drepte într-un plan.

Soluţie

Funcționează conform unui algoritm descris anterior:

x 2 3 + y - 12 = 1 ⇔ 1 2 3 x + 1 - 12 y - 1 = 0 ⇔ ⇔ 3 2 x - 1 12 y - 1 = 0

Răspuns: 3 2 x - 1 12 y - 1 = 0

Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Ecuație în linie dreaptă, unde Ași b unele numere reale, altele decât zero, se numesc ecuația unei drepte în segmente. Acest nume nu este întâmplător, deoarece valorile absolute ale numerelor Ași b egală cu lungimile segmentelor pe care linia dreaptă le taie pe axele de coordonate Bouși Oi respectiv (segmentele se numără de la origine). Astfel, ecuația unei linii drepte în segmente facilitează construirea acestei linii drepte într-un desen. Pentru a face acest lucru, marcați punctele cu coordonate și într-un sistem de coordonate dreptunghiular pe plan și utilizați o riglă pentru a le conecta cu o linie dreaptă.

De exemplu, să construim o linie dreaptă dată de o ecuație în segmente de forma . Marcați punctele și conectați-le.

Puteți obține informații detaliate despre acest tip de ecuație a unei linii drepte pe un plan în articolul ecuația unei linii drepte în segmente.

Începutul paginii

Sfârșitul lucrării -

Acest subiect aparține:

Algebră și geometrie analitică. Conceptul de matrice, operații pe matrice și proprietățile acestora

Conceptul de operații cu matrice pe matrice și proprietățile lor .. o matrice este un tabel dreptunghiular format din numere care nu pot fi .. iar adunarea matricei este o operație în funcție de elemente ..

Dacă aveți nevoie de material suplimentar pe această temă, sau nu ați găsit ceea ce căutați, vă recomandăm să utilizați căutarea în baza noastră de date de lucrări:

Ce vom face cu materialul primit:

Dacă acest material s-a dovedit a fi util pentru dvs., îl puteți salva pe pagina dvs. de pe rețelele sociale:

tweet

Toate subiectele din această secțiune:

Definiţia differentiability
Operația de găsire a derivatei se numește diferențiere a unei funcții. Se spune că o funcție este diferențiabilă la un moment dat dacă are o derivată finită în acel punct și

Regula de diferențiere
Corolarul 1. Factorul constant poate fi scos din semnul derivatei:

Sensul geometric al derivatului. Ecuația tangentei
Unghiul de înclinare al dreptei y \u003d kx + b este unghiul măsurat din poziție

Semnificația geometrică a derivatei unei funcții într-un punct
Se consideră secanta AB a graficului funcției y = f(x) astfel încât punctele A și B au coordonate, respectiv

Soluţie
Funcția este definită pentru toate numerele reale. Deoarece (-1; -3) este punctul de contact, atunci

Condiții necesare pentru un extrem și condiții suficiente pentru un extrem
Definiția unei funcții crescătoare. Funcția y = f(x) crește pe intervalul X dacă pentru oricare

Criterii suficiente pentru extremul unei funcții
Pentru a găsi maximele și minimele funcției, puteți utiliza oricare dintre cele trei semne suficiente ale unui extremum. Deși cel mai comun și convenabil este primul dintre ele.

Proprietățile de bază ale unei integrale definite. Proprietatea 1. Derivata unei integrale definite fata de limita superioara este egala cu integrandul in care, in loc de o variabila, este integrata

Formula Newton-Leibniz (cu dovezi)
formula Newton-Leibniz. Fie funcția y = f(x) continuă pe un segment și F(x) una dintre antiderivatele funcției pe acest segment, atunci

Să fie dat un sistem de coordonate afine OXY.

Teorema 2.1. Orice drept l sistemul de coordonate OX este dat de o ecuație liniară de forma

A X+ B y+ C = O, (1)

unde A, B, C R și A 2 + B 2 0. În schimb, orice ecuație de forma (1) definește o dreaptă.

Ecuația formei (1) - ecuația generală a unei drepte .

Fie în ecuația (1) toți coeficienții A, B și C nenuli. Atunci

Ah-By=-C și .

Să notăm -C/A=a, -C/B=b. obține

-ecuația segmentului drept .

Într-adevăr, numerele |a| și |b| indicați dimensiunea segmentelor tăiate printr-o linie dreaptă l pe axele OX și, respectiv, OY.

Lasă linia l este dat de ecuația generală (1) într-un sistem de coordonate dreptunghiular și fie punctele M 1 (x 1, y 1) și M 2 (x 2, y 2) să aparțină l. Atunci

A X 1 + B la 1 + C = A X 2 + B la 2 + C, adică A( X 1 -X 2) + B( la 1 -la 2) = 0.

Ultima egalitate înseamnă că vectorul \u003d (A, B) este ortogonal cu vectorul \u003d (x 1 -x 2, y 1 -y 2). acestea. Se numește vectorul (A, B). vector normal al dreptei l.

Se consideră vectorul = (-B, A). Atunci

A(-B)+BA=0. acestea. ^ .

Prin urmare, vectorul \u003d (-B, A) este vectorul de direcție al picantului l.

Ecuații parametrice și canonice ale unei drepte

Ecuația unei drepte care trece prin două puncte date

Fie dată linia dreaptă în sistemul de coordonate afine (0, X, Y) l, vectorul său de direcție = (m,n) și punctul M 0 ( X 0 ,y 0) deținut l. Atunci pentru un punct arbitrar M ( X,la) din această linie avem

iar de atunci .

Dacă desemnăm şi

Vectorii rază ai punctelor M și respectiv M 0 , atunci

- ecuația unei drepte sub formă vectorială.

Pentru ca =( X,la), =(X 0 ,la 0), atunci

X= X 0 + mt,

y= y 0 + nt

- ecuația parametrică a unei linii drepte .

De aici rezultă că

- ecuația canonică a unei linii drepte .

În cele din urmă, dacă pe o linie dreaptă l două puncte M 1 ( X 1 ,la 1) și

M2( X 2 ,la 2), atunci vectorul =( X 2 -X 1 ,y 2 -la 1) este îndrumător vector linie dreaptă l. Atunci

- ecuația unei drepte care trece prin două puncte date.

Dispunerea reciprocă a două linii drepte.

Lasă drept l 1 și l 2 sunt date de ecuațiile lor generale

l 1: A 1 X+ În 1 la+ С 1 = 0, (1)

l 2: A 2 X+ B 2 la+ C2 = 0.

Teorema. Lasă drept l 1 și l 2 sunt date de ecuațiile (1). Atunci și numai atunci:

1) liniile se intersectează când nu există un număr λ astfel încât

A1 =λA2, B1 =λB2;

2) liniile coincid când există un număr λ astfel încât

A1 =λA2, B1 =λB2, C1 =λC2;

3) dreptele sunt distincte și paralele când există un număr λ astfel încât

A 1 \u003d λA 2, B 1 \u003d λB 2, C 1 λC 2.

mănunchi de linii drepte

O grămadă de linii drepte este colecția tuturor liniilor din plan care trec printr-un punct numit centru grindă.

Pentru a specifica ecuația fasciculului, este suficient să cunoașteți oricare două linii drepte l 1 și l 2 trecând prin centrul grinzii.

Lăsați liniile din sistemul de coordonate afine l 1 și l 2 sunt date de ecuații

l 1:A1 X+B1 y+ C1 = 0,

l 2:A2 X+ B2 y+ C2 = 0.

Ecuația:

A 1 X+B1 y+ С + λ (A 2 X+ B 2 y+ C) = 0

- ecuația unui creion de linii definite de ecuațiile l 1 și l 2.

În cele ce urmează, prin sistem de coordonate înțelegem sistemul de coordonate dreptunghiular .

Condiții de paralelism și perpendicularitate a două drepte

Lasă liniile l 1 și l 2. cu ecuațiile lor generale; = (A 1 ,B 1), = (A 2 ,B 2) sunt vectorii normali ai acestor drepte; k 1 = tanα 1 , k 2 = tgα 2 – coeficienți de pantă; =( m 1 ,n 1), (m 2 ,n 2) sunt vectori de direcție. Apoi, direct l 1 și l 2 sunt paralele dacă și numai dacă una dintre următoarele condiții este adevărată:

sau oricare k 1 =k 2 sau .

Să fie drept acum l 1 și l 2 sunt perpendiculare. Atunci, evident, , adică A 1 A 2 + B 1 B 2 = 0.

Dacă drept l 1 și l 2 sunt date respectiv de ecuații

l 1: la=k 1 X+ b 1 ,

l 2: la=k 2 X+ b 2 ,

atunci tgα 2 = tg(90º+α) = .

De aici rezultă că

În cele din urmă, dacă și sunt vectorii de direcție ai liniilor, atunci ^ , i.e.

m 1 m 2 + n 1 n 2 = 0

Ultima relație exprimă condiția necesară și suficientă pentru ca două plane să fie perpendiculare.

Unghiul dintre două linii

La un unghi φ între două drepte l 1 și l 2 vom înțelege cel mai mic unghi prin care trebuie rotită o dreaptă astfel încât să devină paralelă cu o altă dreaptă sau să coincidă cu ea, adică 0 £ φ £

Fie dreptele date prin ecuații generale. Este evident că

cosφ=

Să fie drept acum l 1 și l 2 este dat de ecuații cu coeficienți de pantă k 1 in k 2 respectiv. Atunci

Evident, adică ( X-X 0) + B( la-la 0) + C( z-z 0) = 0

Să deschidem parantezele și să notăm D \u003d -A X 0 - B la 0 - C z 0 . obține

A X+ B y+ C z+ D = 0 (*)

- ecuația planului general sau ecuația planului general.

Teorema 3.1 Ecuația liniară (*) (A 2 +B 2 +C 2 ≠ 0) este ecuația planului și invers, orice ecuație a planului este liniară.

1) D = 0, atunci planul trece prin origine.

2) A \u003d 0, atunci planul este paralel cu axa OX

3) A \u003d 0, B \u003d 0, atunci planul este paralel cu planul OXY.

Fie toți coeficienții din ecuație să fie nenuli.

- ecuația unui plan în segmente. Numerele |a|, |b|, |c| indicați dimensiunea segmentelor tăiate de plan pe axele de coordonate.

Ecuația unei drepte în segmente

Să fie dată ecuația generală a unei drepte:

Ecuația unei linii drepte în segmente, unde sunt segmentele pe care linia dreaptă le taie pe axele de coordonate corespunzătoare.

Construiți o dreaptă dată de ecuația generală:

Din care, puteți construi ecuația acestei linii drepte în segmente:

Dispunerea reciprocă a liniilor drepte pe un plan.

Afirmația 1.

Pentru drepte și date de ecuații:

Coincident, necesar și suficient că:

Dovada: și coincid, vectorii lor de direcție și sunt coliniari, adică:

Să luăm punctul M 0 cu aceste drepte, atunci:

Înmulțind prima ecuație cu și adunând la a doua, datorită (2) obținem:

Deci, formulele (2), (3) și (4) sunt echivalente. Fie (2), atunci ecuațiile sistemului (*) sunt echivalente; liniile corespunzătoare coincid.

Afirmația 2.

Dreptele și date de ecuațiile (*) sunt paralele și nu coincid dacă și numai dacă:

Dovada:

Lasă-le să nu se potrivească:

Inconsecvent, adică conform teoremei Kronecker-Capelli:

Acest lucru este posibil numai dacă:

Adică sub condiția (5).

Când prima egalitate (5) este îndeplinită, - neîndeplinirea celei de-a doua egalități dă inconsecvența sistemului (*) liniile sunt paralele și nu coincid.

Observație 1.

Sistemul de coordonate polare.

Fixăm un punct din avion și îl numim stâlp. Raza care emană de la pol se numește axă polară.

Alegem o scară pentru măsurarea lungimii segmentelor și suntem de acord că rotația în sens invers acelor de ceasornic în jurul lui m va fi considerată pozitivă. Luați în considerare orice punct dintr-un plan dat, notați-l prin distanța sa până la pol și numiți-l raza polară. Unghiul cu care axa polară trebuie rotită astfel încât să coincidă cu este notat cu și va fi numit unghi polar.

Definiția 3.

Coordonatele polare ale unui punct sunt raza polară și unghiul polar:

Observaţia 2. la stâlp. Valoarea pentru alte puncte decât un punct este determinată până la un termen.

Să considerăm un sistem de coordonate dreptunghiular cartezian: polul coincide cu originea, iar axa polară coincide cu semiaxa pozitivă. Aici. Atunci:

Care este relația dintre sistemele de coordonate carteziene dreptunghiulare și cele polare.

Ecuația lemniscatei lui Bernoulli. Notează-l în coordonate polare.

Ecuația normală a unei drepte într-un plan. Fie ca axa polară să coincidă cu, - axa care trece prin origine. Lăsa:

Lasă atunci:

Condiție (**) pentru un punct:

Ecuația unei drepte în sistemul de coordonate polare.

Aici - lungimea trasată de la origine la linie dreaptă, - unghiul de înclinare a normalei față de axă.

Ecuația (7) poate fi rescrisă:

Ecuația normală a unei drepte într-un plan.

Proprietățile unei drepte în geometria euclidiană.

Există infinit de linii care pot fi trase prin orice punct.

Prin oricare două puncte care nu coincid, există o singură linie dreaptă.

Două drepte non-coincidente în plan fie se intersectează într-un singur punct, fie sunt

paralel (urmează din precedentul).

În spațiul tridimensional, există trei opțiuni pentru poziția relativă a două linii:

• liniile se intersectează;

• liniile drepte sunt paralele;

• linii drepte se intersectează.

Drept linia- curba algebrică de ordinul întâi: în sistemul de coordonate carteziene, o dreaptă

este dat pe plan de o ecuație de gradul I (ecuație liniară).

Ecuația generală a unei drepte.

Definiție. Orice dreaptă din plan poate fi dată printr-o ecuație de ordinul întâi

Ah + Wu + C = 0,

și constantă A, B nu este egal cu zero în același timp. Această ecuație de ordinul întâi se numește general

ecuație în linie dreaptă.În funcție de valorile constantelor A, Bși CU Sunt posibile următoarele cazuri speciale:

. C = 0, A ≠ 0, B ≠ 0- linia trece prin origine

. A = 0, B ≠0, C ≠0 ( Prin + C = 0)- linie dreaptă paralelă cu axa Oh

. B = 0, A ≠ 0, C ≠ 0 ( Ax + C = 0)- linie dreaptă paralelă cu axa OU

. B = C = 0, A ≠ 0- linia coincide cu axa OU

. A = C = 0, B ≠ 0- linia coincide cu axa Oh

Ecuația unei linii drepte poate fi reprezentată în diferite forme în funcție de orice dat

condiții inițiale.

Ecuația unei drepte printr-un punct și un vector normal.

Definiție. Într-un sistem de coordonate dreptunghiular cartezian, un vector cu componente (A, B)

perpendicular pe dreapta dată de ecuație

Ah + Wu + C = 0.

Exemplu. Aflați ecuația unei drepte care trece printr-un punct A(1, 2) perpendicular pe vector (3, -1).

Soluţie. Să compunem la A \u003d 3 și B \u003d -1 ecuația dreptei: 3x - y + C \u003d 0. Pentru a găsi coeficientul C

substituim coordonatele punctului dat A in expresia rezultata, obtinem: 3 - 2 + C = 0, deci

C = -1. Total: ecuația dorită: 3x - y - 1 \u003d 0.

Ecuația unei drepte care trece prin două puncte.

Să fie date două puncte în spațiu M 1 (x 1 , y 1 , z 1)și M2 (x 2, y 2 , z 2), atunci ecuație în linie dreaptă,

trecând prin aceste puncte:

Dacă oricare dintre numitori este egal cu zero, numărătorul corespunzător trebuie setat egal cu zero. Pe

plan, ecuația unei drepte scrisă mai sus este simplificată:

dacă x 1 ≠ x 2și x = x 1, dacă x 1 = x 2 .

Fracțiune = k numit factor de pantă Drept.

Exemplu. Aflați ecuația unei drepte care trece prin punctele A(1, 2) și B(3, 4).

Soluţie. Aplicând formula de mai sus, obținem:

Ecuația unei drepte după un punct și o pantă.

Dacă ecuația generală a unei drepte Ah + Wu + C = 0 aduce la forma:

și desemnează , atunci ecuația rezultată se numește

ecuația unei drepte cu panta k.

Ecuația unei drepte pe un punct și un vector de direcție.

Prin analogie cu punctul care are în vedere ecuația unei linii drepte prin vectorul normal, puteți intra în sarcină

o dreaptă printr-un punct și un vector de direcție al unei drepte.

Definiție. Fiecare vector diferit de zero (α 1 , α 2), ale căror componente satisfac condiția

Aα 1 + Bα 2 = 0 numit vector de direcție al dreptei.

Ah + Wu + C = 0.

Exemplu. Aflați ecuația unei drepte cu vector de direcție (1, -1) și care trece prin punctul A(1, 2).

Soluţie. Vom căuta ecuația dreptei dorite sub forma: Ax + By + C = 0. Conform definiției,

coeficienții trebuie să îndeplinească condițiile:

1 * A + (-1) * B = 0, adică A = B.

Atunci ecuația unei drepte are forma: Ax + Ay + C = 0, sau x + y + C / A = 0.

la x=1, y=2 primim C/ A = -3, adică ecuația dorită:

x + y - 3 = 0

Ecuația unei drepte în segmente.

Dacă în ecuația generală a dreptei Ah + Wu + C = 0 C≠0, atunci, împărțind la -C, obținem:

sau unde

Sensul geometric al coeficienților este că coeficientul a este coordonata punctului de intersecție

drept cu ax Oh, A b- coordonata punctului de intersecție a dreptei cu axa OU.

Exemplu. Este dată ecuația generală a unei drepte x - y + 1 = 0. Găsiți ecuația acestei drepte în segmente.

C \u003d 1, , a \u003d -1, b \u003d 1.

Ecuația normală a unei linii drepte.

Dacă ambele părți ale ecuației Ah + Wu + C = 0împărțiți la număr , Care e numit

factor de normalizare, apoi primim

xcosφ + ysinφ - p = 0 -ecuația normală a unei linii drepte.

Semnul ± al factorului de normalizare trebuie ales astfel încât μ * C< 0.

R- lungimea perpendicularei coborâte de la origine la linie,

A φ - unghiul format de aceasta perpendiculara cu directia pozitiva a axei Oh.

Exemplu. Având în vedere ecuația generală a unei drepte 12x - 5y - 65 = 0. Necesar pentru a scrie diferite tipuri de ecuații

această linie dreaptă.

Ecuația acestei drepte în segmente:

Ecuația acestei drepte cu panta: (împarte la 5)

Ecuația unei linii drepte:

cos φ = 12/13; sin φ= -5/13; p=5.

Trebuie remarcat faptul că nu orice linie dreaptă poate fi reprezentată printr-o ecuație în segmente, de exemplu, linii drepte,

paralel cu axele sau trecând prin origine.

Unghiul dintre liniile unui plan.

Definiție. Dacă sunt date două rânduri y \u003d k 1 x + b 1, y \u003d k 2 x + b 2, apoi unghiul ascuțit dintre aceste linii

va fi definit ca

Două drepte sunt paralele dacă k 1 = k 2. Două drepte sunt perpendiculare

dacă k 1 \u003d -1 / k 2 .

Teorema.

Direct Ah + Wu + C = 0și A 1 x + B 1 y + C 1 \u003d 0 sunt paralele când coeficienții sunt proporționali

A 1 \u003d λA, B 1 \u003d λB. Dacă de asemenea С 1 \u003d λС, apoi liniile coincid. Coordonatele punctului de intersecție a două drepte

se găsesc ca soluție a sistemului de ecuații ale acestor drepte.

Ecuația unei drepte care trece printr-un punct dat este perpendiculară pe o dreaptă dată.

Definiție. Linie care trece printr-un punct M 1 (x 1, y 1)și perpendicular pe linie y = kx + b

reprezentată de ecuația:

Distanța de la un punct la o linie.

Teorema. Dacă se acordă un punct M(x 0, y 0), apoi distanța până la linie Ah + Wu + C = 0 definit ca:

Dovada. Lasă punctul M 1 (x 1, y 1)- baza perpendicularei coborâtă din punct M pentru un dat

direct. Apoi distanța dintre puncte Mși M 1:

(1)

Coordonatele x 1și 1 poate fi găsită ca soluție a sistemului de ecuații:

A doua ecuație a sistemului este ecuația unei drepte care trece perpendicular printr-un punct dat M 0

linie dată. Dacă transformăm prima ecuație a sistemului în forma:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

apoi, rezolvand, obtinem:

Înlocuind aceste expresii în ecuația (1), găsim:

Teorema a fost demonstrată.