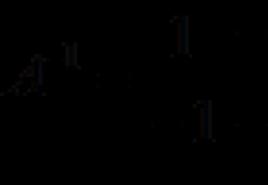Regulārs piecstūris ar kompasiem. Apli sadalot vienādās daļās un uzrakstot regulārus daudzstūrus

Grūtības pakāpe: viegli

1. solis

Vispirms izvēlieties, kur novietot apļa centru. Tur jums jāievieto sākuma punkts, ļaujiet tam saukties O. Ar kompasa palīdzību ap to noformē noteikta diametra vai rādiusa apli.

2. solis

Tad mēs izvelk divas asis caur punktu O, apļa centru, vienu horizontāli, otru 90 grādu leņķī attiecībā pret to - vertikāli. Krustojuma punkti horizontāli tiks izsaukti no kreisās puses uz labo A un B, vertikāli, no augšas uz leju - M un N. Radiuss, kas atrodas uz jebkuras ass, piemēram, uz horizontāles labajā pusē, ir sadalīts uz pusēm. To var izdarīt šādi: ar galu horizontālās ass un apļa krustojumā tiek noteikts kompass ar mums zināma apļa rādiusu - B, mēs norobežojam krustojumus ar apli, iegūtie punkti tiek attiecīgi saukti no augšas uz leju - C un P, mēs tos savienojam ar segmentu, kas šķērsos OB asi, krustojuma punktu sauc par K.

3. solis

Mēs savienojam punktus K un M un iegūstam segmentu KM, punktā M uzstādām kompasu, uz tā uzstādām attālumu līdz punktam K un izklāsta zīmes uz rādiusu OA, mēs saucam šo punktu E, pēc tam zīmējam kompasu, līdz tas krustojas ar apļa OM augšējo kreiso daļu. Šo krustošanās punktu sauc par F. Attālums, kas vienāds ar segmentu ME, ir vienādmalu piecstūra vēlamā puse. Šajā gadījumā punkts M būs viena piecstūra virsotne, kas iestrādāts aplī, un punkts F būs cits.

4. solis

Tālāk no iegūtajiem punktiem visā aplī mēs ar kompasu zīmējam attālumus, kas vienādi ar ME segmentu, kopējam punktu skaitam jābūt 5. Visus punktus savienojam ar segmentiem - iegūstam apli ierakstītu piecstūri.

• Zīmējot, esiet uzmanīgs, mērot attālumus, nepieļaujiet kļūdas, lai piecstūris tiešām izrādītos vienādmalu

Izveido regulāru sešstūri, kas ierakstīts aplī.

Sešstūra konstrukcija balstās uz faktu, ka tā mala ir vienāda ar apvilktās apļa rādiusu. Tāpēc būvniecībai pietiek ar apļa sadalīšanu sešās vienādās daļās un atrasto punktu savienošanu ar otru.

Regulāru sešstūri var uzbūvēt, izmantojot sliedi un 30X60 ° kvadrātu. Lai veiktu šo konstrukciju, par 1. un 4. leņķa bisektoru mēs ņemam apļa horizontālo diametru, izveidojam 1 - 6, 4 - 3, 4 - 5 un 7 - 2 malas un pēc tam uzzīmējam malas 5 - 6 un 3 - 2.

Šāda trīsstūra virsotnes var veidot, izmantojot kompasu un kvadrātu ar 30 un 60 ° leņķi vai tikai vienu kompasu. Apsveriet divus veidus, kā veidot vienādmalu trīsstūri, kas ierakstīts aplī.

Pirmais ceļš (61. att., A) ir balstīts uz faktu, ka visi trīs trīsstūra 7, 2, 3 leņķi satur 60 °, un vertikālā līnija, kas novilkta caur punktu 7, ir gan leņķa 1 augstums, gan bisektors. Tā kā leņķis 0 - 1 - 2 ir vienāds ar 30 °, tad, lai atrastu sānu 1 - 2, pietiek ar 30 ° leņķa izveidošanu 1. punktā un sānu 0–1. Lai to izdarītu, uzstādiet sacīkšu trasi un kvadrātu, kā parādīts attēlā, uzzīmējiet līniju 1 - 2, kas būs viena no vēlamā trīsstūra malām. Lai izveidotu 2. – 3. Malu, novietojiet sacīkšu ceļu pozīcijā, ko norāda ar pārtrauktām līnijām, un caur punktu 2 novelciet taisnu līniju, kas noteiks trīsstūra trešo virsotni.

Otrais ceļš balstās uz faktu, ka, izveidojot regulāru sešstūri, kas ierakstīts aplī, un pēc tam savienojot tā virsotnes caur vienu, jūs iegūstat vienādmalu trīsstūri.

Lai izveidotu trīsstūri, atzīmējiet punktu 1 uz virsotnes diametru un uzzīmējiet diametrālu līniju 1 - 4. Tālāk no 4. punkta ar rādiusu D / 2 mēs aprakstām loka līdz krustojumam ar apli punktos 3 un 2. Rezultātā iegūtie punkti būs vēl divi vēlamā trīsstūra virsotnes.

Šo konstrukciju var veikt, izmantojot kvadrātu un kompasu.

Pirmais ceļš pamatojoties uz to, ka kvadrāta diagonāles krustojas apzīmētā apļa centrā un ir slīpi pret tā asīm 45 ° leņķī. Balstoties uz to, mēs uzstādām lidojuma riepu un kvadrātu ar 45 ° leņķi, kā parādīts 1. attēlā. 62, a, un atzīmējiet 1. un 3. punktu. Tālāk caur šiem punktiem ar lidojuma riepas palīdzību mēs zīmējam kvadrāta horizontālās malas 4 - 1 un 3 -2. Tad ar sacīkšu palīdzību gar laukuma kāju mēs uzzīmējam kvadrāta vertikālās malas 1 - 2 un 4 - 3.

Otrais ceļš balstās uz faktu, ka kvadrāta virsotnes šķērso apļveida loka, kas ir slēgtas starp diametra galiem. Mēs atzīmējam divu savstarpēji perpendikulāru diametru punktu A, B un C galos un no tiem ar rādiusu y aprakstam lokus līdz to savstarpējam krustojumam.

Pēc tam caur loku krustošanās punktiem uzzīmējiet taisnas palīglīnijas, kas uz figūras ir marķētas ar cietām līnijām. Viņu krustošanās punkti ar apli nosaka 1. un 3. virsotni; 4 un 2. Šādi iegūtās vajadzīgā kvadrāta virsotnes ir savstarpēji savienotas virknē.

Regulāra piecstūra izveidošana, kas ierakstīts aplī.

Lai aplī iestiprinātu parasto piecstūri, mēs izgatavojam šādas konstrukcijas. Mēs atzīmējam 1. punktu uz apļa un uztveram to kā vienu no piecstūra virsotnēm. Sadaliet AO segmentu uz pusēm. Lai to izdarītu, ar rādiusu AO no punkta A mēs aprakstām loka līdz krustojumam ar apli punktos M un B. Savienojot šos punktus ar taisnu līniju, mēs iegūstam punktu K, kuru mēs pēc tam savienojam ar punktu 1. Ar rādiusu, kas vienāds ar segmentu A7, mēs aprakstām loka no punkta K līdz krustojumam ar diametru. līnija AO punktā H. Savienojot punktu 1 ar punktu H, mēs iegūstam piecstūra pusi. Tad ar kompasa risinājumu, kas vienāds ar segmentu 1H, aprakstot loku no 1. virsotnes līdz krustojumam ar apli, mēs atrodam 2. un 5. virsotni. Izgatavojot to pašu kompasa risinājumu iecirtumiem no 2. un 5. virsotnes, iegūstam atlikušās virsotnes 3 un 4. Atrasti punkti tiek secīgi savienoti viens ar otru.

Izveido regulāru piecstūri pa doto pusi.

Lai konstruētu regulāru piecstūri gar tā doto pusi (64. att.), Mēs sadalām segmentu AB sešās vienādās daļās. No punktiem A un B ar rādiusu AB mēs aprakstām lokus, kuru krustojums sniegs punktu K. Caur šo punktu un dalījumu 3 ar taisnu līniju AB novelciet vertikālu līniju. Tālāk no K punkta uz šīs taisnās līnijas mēs atdalām segmentu, kas vienāds ar 4/6 AB. Mēs iegūstam 1. punktu - piecstūra augšdaļu. Tad ar rādiusu, kas vienāds ar AB, no 1. punkta mēs aprakstām loka, līdz tā krustojas ar lokiem, kas iepriekš novilkti no punktiem A un B. Loku krustošanās punkti nosaka 2. un 5. piecstūra virsotnes. Mēs atrastās virsotnes savienojam virknē viena ar otru.

Regulāra sešstūra uzbūve aplī.

Dod apli ar diametru D; tajā jāiekļauj parasts sešstūris (65. att.). Apļa vertikālo diametru mēs sadalām septiņās vienādās daļās. Sākot no 7. punkta ar rādiusu, kas vienāds ar apļa D diametru, mēs aprakstām loka līdz krustojumam ar horizontālā diametra turpinājumu punktā F. Punktu F sauksim par daudzstūra polu. Ņemot VII punktu kā vienu no heptagona virsotnēm, no staba F novelciet starus pa vienmērīgiem vertikālā diametra dalījumiem, kuru krustošanās ar apli noteiks heptagona VI, V un IV virsotnes. Lai iegūtu virsotnes / - // - /// no punktiem IV, V un VI, krustojumam ar apli zīmējiet horizontālas līnijas. Mēs savienojam atrastās virsotnes virknē viens ar otru. Heptagonu var izveidot, velkot starus no F pola un pa nepāra vertikālā diametra dalījumiem.

Dotā metode ir piemērota regulāru daudzstūru veidošanai ar jebkuru malu skaitu.

Apļa sadalījumu jebkurā vienādās daļās var veikt arī, izmantojot tabulas 1 datus. 2, kas parāda koeficientus, kas ļauj noteikt parasto uzrakstu daudzstūru sānu izmērus.

Regulāri ierakstītu daudzstūru sānu garums.

Šīs tabulas pirmajā kolonnā parādīts parastā daudzstūra malu skaits, bet otrajā - koeficienti. Dotā daudzstūra malas garumu iegūst, reizinot dotā apļa rādiusu ar koeficientu, kas atbilst šī daudzstūra malu skaitam.

2011. gada 8. jūnijs

Pirmais ceļš - šajā pusē S, izmantojot proraktoru.

Mēs uzzīmē taisnu līniju un uzliek AB \u003d S; mēs šo līniju uztveram kā rādiusu un ar šo rādiusu aprakstam lokus no punktiem A un B: tad, izmantojot prožektoru, šajos punktos veidojam 108 ° leņķus, kuru malas krustojas ar lokiem punktos C un D; no šiem punktiem ar rādiusu AB \u003d 5 mēs aprakstam lokus, kas krustojas E, un ar taisnām līnijām mēs savienojam punktus L, C, E, D, B.

Iegūtais piecstūris - vēlamais.

Otrais ceļš. Uzzīmēsim apli ar rādiusu r. No punkta A ar kompasu novelciet loka rādiusu AM līdz krustojumam punktos B un C ar apli. Savienojiet B un C ar līniju, kas šķērso horizontālo asi E punktā.

Tad no punkta E mēs uzzīmējam loku, kas krustojas ar horizontālo līniju punktā O. Visbeidzot, no punkta F mēs aprakstām loku, kas krusto apli punktos H un K. Piecas reizes liekot attālumu FO \u003d FH \u003d FK un apdalot dalīšanas punktus ar līnijām, mēs iegūstam regulāru piecstūri.

Trešais ceļš. Šajā aplī ierakstiet parasto piecstūri. Mēs uzzīmējam divus savstarpēji perpendikulārus diametrus AB un MC. AO rādiusu daliet ar punktu E uz pusēm. No punkta E, tāpat kā no centra, mēs uzzīmējam apļa rādiusa EM loka un atzīmējam to ar diametru AB punktā F. Segments MF ir vienāds ar vajadzīgā regulārā piecstūra malu. Ar kompasu, kas vienāds ar MF, mēs izveidojam serifus N 1, P 1, Q 1, K 1 un savienojam tos ar taisnām līnijām.

Attēlā ir parādīts sešstūris šajā pusē.

Taisna līnija AB \u003d 5 kā rādiuss no punktiem A un B apraksta loka, kas krustojas C; no šī brīža ar tādu pašu rādiusu mēs aprakstām loku, uz kuru pusi A B tiks novietots 6 reizes.

Sešstūris ADEFGB- vēlamais.

"Istabu rotāšana renovācijas laikā",
N. P. Krasnovs

Pirmais veids, kā veidot. Mēs uzzīmējam horizontālās (AB) un vertikālās (CD) asis un no to krustošanās punkta M mēs novietojam pusass attiecīgajā skalā. Mēs uzzīmējam daļēji mazo asi no punkta M uz galvenās ass līdz punktam E. Elipse, pirmā konstruēšanas metode Sadaliet BE divās daļās un vienu no galvenās ass M no punkta M uzklājiet (uz F vai H) ...

Gleznas pamatā ir pilnībā pabeigta sienu, griestu un citu konstrukciju virsmas krāsošana; krāsošana tiek veikta, izmantojot augstas kvalitātes līmi un eļļas krāsas, kas izgatavotas apgriešanai vai flutēšanai. Sākot izstrādāt apdares skici, kapteinim skaidri jāiedomājas viss skaņdarbs sadzīviskā vidē un skaidri jāsaprot radošais nodoms. Tikai tad, ja šis pamatnosacījums ir izpildīts, ir iespējams pareizi ...

Veiktā darba mērījumus, izņemot īpaši noteiktus gadījumus, veic atbilstoši faktiski apstrādājamās virsmas laukumam, ņemot vērā tā reljefu un mīnus neapstrādātas vietas. Lai noteiktu patiešām apstrādātas virsmas krāsošanas laikā, izmantojiet tabulās norādītos pārrēķina koeficientus. A. Koka logu ierīces (mērījumus veic atbilstoši atveru laukumam gar kastu ārējo kontūru) Ierīču nosaukums Koeficients pie ...

Parasts piecstūris ir ģeometriska forma, ko veido piecu taisnu līniju krustojums, kas veido piecus vienādus stūrus. Šādu skaitli sauc par Pentagonu. Mākslinieku darbi ir cieši saistīti ar piecstūri - viņu zīmējumi balstās uz regulārām ģeometriskām formām. Lai to izdarītu, jums jāzina, kā ātri izveidot piecstūri.

Kas ir interesants par šo skaitli? Ēkai ir piecstūra forma Amerikas Savienoto Valstu Aizsardzības departaments... To var redzēt fotogrāfijās, kas uzņemtas no lidojuma augstuma. Dabā nav kristālu un akmeņu, kuru forma atgādinātu piecstūri. Tikai šajā attēlā seju skaits sakrīt ar diagonāļu skaitu.

Regulāras piecstūra iespējas

Taisnstūra piecstūrim, tāpat kā katrai formai ģeometrijā, ir savi parametri. Zinot nepieciešamās formulas, jūs varat aprēķināt šos parametrus, kas atvieglos piecstūra veidošanas procesu. Aprēķina metodes un formulas:

• visu leņķu summa daudzstūros ir 360 grādi. Parastā piecstūrī visi leņķi ir vienādi, attiecīgi centrālais leņķis tiek noteikts: 360/5 \u003d 72 grādi;
• iekšējais leņķis tiek atrasts šādā veidā: 180 * (n -2) / n \u003d 180 * (5-2) / 5 \u003d 108 grādi. Visu iekšējo leņķu summa: 108 * 5 \u003d 540 grādi.

Piecstūra puse ir atrasta, izmantojot parametrus, kas jau ir norādīti problēmas paziņojumā:

• ja ap piecstūri ir aprakstīts aplis un ir zināms tā rādiuss, malu atrod pēc šādas formulas: a \u003d 2 * R * sin (α / 2) \u003d 2 * R * sin (72/2) \u003d 1,1756 * R.
• Ja ir zināms piecstūrī ierakstītā apļa rādiuss, tad daudzstūra malas aprēķināšanas formula: 2 * r * tg (α / 2) \u003d 2 * r * tg (α / 2) \u003d 1,453 * r.
• Ar zināmu piecstūra diagonāles vērtību tā malu aprēķina šādi: a \u003d D / 1,618.

Piecstūra laukums ir vienāds, tāpat kā tā puse, ir atkarīgs no jau atrastajiem parametriem:

• izmantojot zināmo uzrakstītā apļa rādiusu, laukumu nosaka šādi: S \u003d (n * a * r) / 2 \u003d 2,5 * a * r.
• ap piecstūri apzīmētais aplis ļauj atrast apgabalu pēc šādas formulas: S \u003d (n * R2 * sin α) / 2 \u003d 2,33776 * R2.
• atkarībā no piecstūra malas: S \u003d (5 * a2 * iedegums 54 °) / 4 \u003d 1,7205 * a2.

Piecstūra veidošana

Izmantojot lineālu un kompasu, jūs varat izveidot regulāru piecstūri, balstoties uz apli, kas uzrakstīts tajā vai vienā no sāniem.

Kā uzzīmēt piecstūri, pamatojoties uz uzrakstītu apli? Lai to izdarītu, jums jāuzkrāj kompass un lineāls un jāveic šādas darbības:

1. Pirmkārt, jums jāzīmē aplis ar centru O, pēc tam izvēlieties punktu uz tā, A - piecstūra augšdaļa. No centra uz augšu tiek uzzīmēts segments.
2. Tad tiek izveidots līnijas segments, kas ir perpendikulārs līnijai OA, kas iet arī caur O - apļa centru. Tās krustojumu ar apli norāda ar punktu B. Segments O. V. ir sadalīts uz pusēm ar punktu C.
3. C punkts kļūs par jauna apļa centru, kas iet caur A punktu. D punkts ir tā krustojums ar līniju OB pirmā attēla robežās.
4. Pēc tam caur D tiek novilkts trešais aplis, kura centrs ir punkts A. Tas divos punktos krustojas ar pirmo figūru, tie jāapzīmē ar burtiem E un F.
5. Nākamajam lokam ir centrs punktā E un tas iet caur A, un tā krustojums ar oriģinālu atrodas jaunā punktā G.
6. Pēdējais aplis šajā attēlā ir novilkts caur punktu A ar centru F. Punkts H tiek novietots tā krustojumā ar sākotnējo.
7. Pirmajā aplī pēc visiem veiktajiem soļiem parādījās pieci punkti, kuriem jābūt savienotiem ar segmentiem. Tādējādi parasts piecstūris AE G H F.

Kā savādāk izveidot parasto piecstūri? Ar lineālu un kompasu piecstūri var uzbūvēt nedaudz ātrāk. Tam nepieciešams:

1. Pirmkārt, jums ir jāizzīmē aplis, izmantojot kompasu, kura centrā ir punkts O.
2. Tiek novilkts rādiuss OA - segments, kas noteikts uz apļa. To dala uz pusi ar punktu B.
3. Segments OS ir novilkts perpendikulāri rādiusam OA, punkti B un C ir savienoti ar taisnu līniju.
4. Nākamais solis ir iezīmēt BC segmenta garumu, izmantojot kompasu uz centra līnijas. Punkts D parādās perpendikulāri līnijai OA. Punkti B un D ir savienoti, veidojot jaunu līniju.
5. Lai iegūtu piecstūra malas izmēru, ir nepieciešams savienot punktus C un D.
6. D tiek pārsūtīts uz apli ar kompasa palīdzību un tiek apzīmēts ar punktu E. Savienojot E un C, jūs varat iegūt regulārā piecstūra pirmo pusi. Izpildot šo instrukciju, jūs varat uzzināt, kā ātri izveidot piecstūri ar vienādām pusēm, turpinot veidot pārējās tā malas tāpat kā pirmās.

Piecstūrī ar vienādām pusēm diagonāles ir vienādas un veido piecstaru zvaigzni, ko sauc par pentagrammu. Zelta attiecība ir diagonāles un piecstūra malas attiecība.

Pentagons nav piemērots pilnīgai lidmašīnas piepildīšanai. Jebkura materiāla izmantošana šādā formā rada nepilnības vai pārklāšanos. Kaut arī dabiski šādas formas kristāli dabā neeksistē, kad uz gludu vara izstrādājumu virsmas veidojas ledus, parādās piecstūra formas molekulas, kuras ir savienotas ķēdēs.

Vienkāršākais veids, kā no papīra sloksnes iegūt regulāru piecstūri, ir to sasiet mezglā un nedaudz nospiest. Šī metode ir noderīga pirmsskolas vecuma bērnu vecākiem, kuri vēlas iemācīt mazajiem atpazīt ģeometriskās formas.

Video

Uzziniet, kā jūs varat ātri uzzīmēt piecstūri.

5.3. Zelta Pentagons; Eiklida būve.

Brīnišķīgs "zelta attiecības" piemērs ir parasts piecstūris - izliekts un zvaigznes formas (5. att.).

Lai izveidotu pentagrammu, jums jāveido parasts piecstūris.

Ļaujiet O apļa centram, A ir apļa punkts un E segmenta OA viduspunktam. Perpendikulārs rādiuss OA, kas atjaunots punktā O, krustojas ar apli punktā D. Izmantojot kompasu, mēs atlikām segmentu CE \u003d ED uz diametru. Lokā ierakstīta regulāra piecstūra sānu garums ir DC. Mēs noliekam malā segmentus DC uz apļa un iegūstam piecus punktus parastā piecstūra zīmēšanai. Mēs savienojam piecstūra stūrus caur vienu diagonāli un iegūstam pentagrammu. Visas piecstūra diagonāles sadala viena otrai daiviņās, kuras savieno zelta proporcija.

Katrs piecstūra zvaigznes gals ir zelta trīsstūris. Tās malas virsotnē veido 36 ° leņķi, un sānos atstātā pamatne to sadala proporcionāli zelta attiecībai.

Ir arī zelta kuboids - tas ir taisnstūra paralēlskaldnis ar malām, kuru garums ir 1,618, 1 un 0,618.

Tagad apsveriet Eiklida piedāvāto pierādījumu sadaļā "Elementi".

Tagad redzēsim, kā Eiklidads izmanto zelta attiecību, lai izveidotu 72 grādu leņķi - tieši šajā leņķī ir redzama regulārā piecstūra puse.

no aprakstāmā apļa centra. Sāksim ar

segments ABE, sadalīts vidēji un

Tātad, ļaujiet AC \u003d AE. Ar vienlīdzīgu leņķi apzīmēsim EBC un CEB. Tā kā AC \u003d AE, arī ACE leņķis ir vienāds ar a. Teorēma, ka trīsstūra leņķu summa ir 180 grādi, ļauj atrast leņķi VISU: tas ir 180–2a, bet leņķis EAC - 3a –180. Bet tad leņķis ABC ir 180 a. Apkopojot trijstūra ABC leņķus, iegūstam

180 \u003d (3a –180) + (3a – 180) + (180 – a)

No kurienes 5a \u003d 360, tad a \u003d 72.

Tātad katrs no trīsstūra pamatnes leņķiem ir divreiz lielāks par leņķi 36 grādu leņķī. Tāpēc, lai izveidotu regulāru piecstūri, ir jānozīmē tikai jebkurš aplis, kas ir centrā E, krustojot EC punktā X un sānu EB punktā Y: segments XY kalpo kā viena no regulārā piecstūra malām, kas ierakstītas aplī; Apbraucot visu apli, jūs varat atrast visas pārējās puses.

Tagad pierādīsim, ka AC \u003d AE. Pieņemsim, ka virsotni C savieno taisns līnijas segments ar BE segmenta viduspunktu N. Ņemiet vērā, ka, tā kā CB \u003d CE, leņķis СNЕ ir taisns. Pēc Pitagora teorēmas:

CN 2 \u003d a 2 - (a / 2j) 2 \u003d a 2 (1-4j 2)

Tātad mums ir (AC / a) 2 \u003d (1 + 1 / 2j) 2 + (1-1 / 4j 2) \u003d 2 + 1 / j \u003d 1 + j \u003d j 2

Tātad, AC \u003d jа \u003d jAB \u003d AE, kā jāpierāda

5.4 Arhimēdas spirāle.

Secīgi nogriežot kvadrātus no zelta taisnstūriem līdz bezgalībai, katru reizi savienojot pretējos punktus ar ceturtdaļas apli, mēs iegūstam diezgan graciozu līkni. Pirmais, kas viņai pievērsa uzmanību, bija seno grieķu zinātnieks Arhimēds, kura vārdu viņa nes. Viņš to izpētīja un atvasināja šīs spirāles vienādojumu.

Pašlaik Archimedes spirāli plaši izmanto tehnoloģijās.

6. Fibonači skaitļi.

Itāļu matemātiķa Leonardo vārds no Pizas, kurš labāk pazīstams ar savu iesauku Fibonači (Fibonači ir saīsināts filius Bonacci, tas ir, Bonacci dēls), ir netieši saistīts ar zelta attiecību.

1202. gadā. viņš uzrakstīja grāmatu "Liber abacci", tas ir, "Abaka grāmata". "Liber abacci" ir apjomīgs darbs, kas satur gandrīz visu tā laika aritmētisko un algebrisko informāciju, un tam bija nozīmīga loma matemātikas attīstībā Rietumeiropā nākamo vairāku gadsimtu laikā. Proti, caur šo grāmatu eiropieši iepazinās ar hindu (“arābu”) numuriem.

Grāmatā aprakstītais materiāls ir izskaidrots par daudzām problēmām, kas veido nozīmīgu šī traktāta daļu.

Apsveriet vienu no šādām problēmām:

"Cik trušu pāri piedzimst no viena pāra vienā gadā?

Kāds noteiktā vietā ievieto trušu pāri, kas no visām pusēm ir iežogots ar sienu, lai noskaidrotu, cik trušu pāri piedzims šī gada laikā, ja trušu raksturs ir tāds, ka mēnesī trušu pāris atveidos citu, un truši dzemdēs no otrā mēneša pēc viņu piedzimšanas "

Mēneši	1	2	3	4	5	6	7	8	9	10	11	12
Trušu pāris	2	3	5	8	13	21	34	55	89	144	233	377

Pārejam no trušiem uz skaitļiem un apsverim šādu skaitļu secību:

u 1, u 2 ... u n

kurā katrs termins ir vienāds ar iepriekšējo divu summu, t.i. jebkuram n\u003e 2

u n \u003d u n -1 + u n -2.

Šī secība asimptotiski (tuvojas arvien lēnāk) mēdz sasniegt zināmu nemainīgu attiecību. Tomēr šī attiecība ir neracionāla, tas ir, tas ir skaitlis ar bezgalīgu, neparedzamu decimālo ciparu secību frakcionētajā daļā. Precīzi to nav iespējams izteikt.

Ja kāds Fibonači secības loceklis tiek dalīts ar to, kas atrodas pirms tā (piemēram, 13: 8), rezultāts būs vērtība, kas svārstās ap iracionālo vērtību 1,61803398875 ... un dažreiz to pārspēj vai nesasniedz.

Asimptotiska sekvences izturēšanās, slāpējot tās attiecības svārstības ap neracionālu skaitli Ф, var kļūt skaidrāka, ja parādīsim vairāku pirmo sekvences locekļu attiecības. Šis piemērs parāda otrā vārda attiecības ar pirmo, trešo līdz otro, ceturto līdz trešo un tā tālāk:

1: 1 \u003d 1,0000, kas ir par 0,6180 mazāk phi

2: 1 \u003d 2,0000, kas ir par 0,3820 vairāk phi

3: 2 \u003d 1,5000, kas ir par 0,1180 mazāk phi

5: 3 \u003d 1,6667, kas ir par 0,0486 phi vairāk

8: 5 \u003d 1,6000, kas ir par 0,0180 mazāku phi

Virzoties pa Fibonači summēšanas secību, katrs jaunais termins sadalīs nākamo ar lielāku un lielāku tuvinājumu nepieejamajam F.

Cilvēks zemapziņā meklē dievišķo proporciju: tas ir nepieciešams, lai apmierinātu viņa vajadzību pēc ērtībām.

Sadalot jebkuru Fibonači secības locekli ar nākamo, jūs iegūstat tieši pretēju 1,618 vērtībai (1: 1,618 \u003d 0,618). Bet šī ir arī ļoti neparasta, pat ievērojama parādība. Tā kā sākotnējās attiecības ir bezgalīgas, arī šīm attiecībām nevajadzētu būt beigām.

Sadalot katru skaitli ar nākamo pēc tā, mēs iegūstam skaitli 0,382

Šādi izvēloties koeficientus, iegūstam galveno Fibonači koeficientu kopu: 4.235, 2.618, 1.618,0.618,0.382,0.236. Pieminēsim arī 0.5.Visiem no tiem ir īpaša loma dabā un, jo īpaši, tehniskajā analīzē.

Šeit jāpiebilst, ka Fibonači cilvēcei tikai atgādināja par viņa secību, jo senos laikos tas bija pazīstams ar nosaukumu Zelta attiecība.

Zelta attiecība, kā mēs redzējām, rodas saistībā ar parasto piecstūri, tāpēc Fibonači skaitļiem ir nozīme visā, kas ir saistīts ar regulārajiem piecstūriem - izliektiem un zvaigznēm.

Fibonači sērija varētu palikt tikai par matemātisku atgadījumu, ja ne par to, ka visi augu un dzīvnieku pasaules zelta dalījuma pētnieki, nemaz nerunājot par mākslu, vienmēr nonāca šajā sērijā kā zelta dalīšanas likuma aritmētiskā izpausme. Zinātnieki turpināja aktīvi attīstīt Fibonači skaitļu teoriju un zelta attiecību. Yu Matiyasevich, izmantojot Fibonači skaitļus, atrisina Hilberta 10. problēmu (par diopantīna vienādojumu risināšanu). Ir sarežģītas metodes daudzu kibernētisko problēmu risināšanai (meklēšanas teorija, spēles, programmēšana), izmantojot Fibonači skaitļus un zelta attiecību. ASV pat tiek izveidota Mathematical Fibonacci Association, kas kopš 1963. gada izdod īpašu žurnālu.

Viens no sasniegumiem šajā jomā ir vispārinātu Fibonači skaitļu un vispārinātu zelta koeficientu atklāšana. Fibonači sērija (1, 1, 2, 3, 5, 8) un "binārā" skaitļu sērija 1, 2, 4, 8, 16 ... (tas ir, skaitļu virkne līdz n, kur jebkurš dabiskais skaitlis ir mazāks par n var attēlot kā dažu skaitļu summu šajā sērijā), no pirmā acu uzmetiena, ir pilnīgi atšķirīgi. Bet to uzbūves algoritmi ir ļoti līdzīgi viens otram: pirmajā gadījumā katrs skaitlis ir iepriekšējā skaitļa summa ar sevi 2 \u003d 1 + 1; 4 \u003d 2 + 2 ..., otrajā tā ir divu iepriekšējo skaitļu summa 2 \u003d 1 + 1, 3 \u003d 2 + 1, 5 \u003d 3 + 2 .... Vai ir iespējams atrast vispārīgu matemātisko formulu, no kuras un " bināro ”un Fibonači sēriju?

Patiešām, uzstādīsim skaitlisku parametru S, kam var būt jebkuras vērtības: 0, 1, 2, 3, 4, 5 ... Apsveriet skaitlisku sēriju, kuras pirmo nosacījumu S + 1 ir vieni, un katrs nākamais ir vienāds ar iepriekšējā un divu nosacījumu summu. attālums no iepriekšējā pa S pakāpieniem. Ja mēs apzīmējam šīs sērijas n-to termiņu ar S (n), tad iegūstam vispārīgo formulu S (n) \u003d S (n - 1) + S (n - S - 1).

Acīmredzami, ka S \u003d 0 no šīs formulas mēs iegūstam "bināro" sēriju, S \u003d 1 - Fibonači sēriju ar S \u003d 2, 3, 4. jaunas skaitļu sērijas, kuras sauc par S-Fibonači skaitļiem.

Kopumā zeltainā S proporcija ir zelta S koeficienta vienādojuma x S + 1 - x S - 1 \u003d 0 pozitīvā sakne.

Ir viegli parādīt, ka tad, kad S \u003d 0, segments tiek sadalīts uz pusēm un kad S \u003d 1, pazīstamā klasiskā zelta attiecība.

Blakusesošo Fibonači S skaitļu attiecības sakrīt ar absolūto matemātisko precizitāti, kas robežojas ar zelta S proporcijām! Tas ir, zelta S koeficienti ir Fibonači S skaitļu skaitliskie invarianti.

7.Zelta attiecība mākslā.

7.1. Zelta attiecība glezniecībā.

Pārejot pie "zelta attiecības" piemēriem glezniecībā, nevar pievērst uzmanību Leonardo da Vinči darbam. Viņa personība ir viena no vēstures noslēpumiem. Pats Leonardo da Vinči sacīja: "Lai neviens, nebūdams matemātiķis, neuzdrošināsies lasīt manus darbus."

Nav šaubu, ka Leonardo da Vinči bija lielisks mākslinieks, un to jau atzina viņa laikabiedri, taču viņa personība un aktivitātes paliks noslēpumā noslēptas, jo viņš atstāja pēcnācējus nevis saskaņotu savu ideju izklāstu, bet tikai neskaitāmas ar roku rakstītas skices, piezīmes, kas saka “par” viss pasaulē. "

Monnas Lizas (La Gioconda) portrets daudzus gadus ir piesaistījis pētnieku uzmanību, kuri atklāja, ka zīmējuma kompozīcija ir balstīta uz zelta trīsstūriem, kas ir regulāra zvaigžņu formas piecstūra daļas ..

Arī Šiškina gleznā parādās zelta proporcijas proporcija. Šajā slavenajā I.I.Šiškina gleznā skaidri redzami zelta sekcijas motīvi. Priedes koks, ko spoži apgaismo saule (priekšplānā), gleznas garumu sadala pa zelta proporciju. Priedes labajā pusē atrodas saules apspīdēts paugurs. Attēla labo pusi viņš horizontāli sadala pa zelta proporciju.

Rafaēla gleznā "Zīdaiņu sišana" ir redzams vēl viens zelta proporcijas elements - zelta spirāle. Uz Rafaela sagatavojošās skices no kompozīcijas semantiskā centra tiek novilktas sarkanas līnijas - vietas, kur karavīra pirksti aizvērās ap bērna potīti - gar bērna figūrām, sieviete tur viņu tuvu, karotājs ar novilktu zobenu un pēc tam gar tās pašas grupas figūrām skices labajā pusē. ... Nav zināms, vai Rafaels uzcēla vai sajuta zelta spirāli.

T. Kuks izmantoja zelta sadaļu Sandro Botičeli gleznas "Venēras dzimšana" analīzē.

7.2. Zelta proporcijas piramīdas.

Piramīdu medicīniskās īpašības, īpaši zelta attiecība, ir plaši zināmas. Saskaņā ar dažiem visizplatītākajiem viedokļiem telpa, kurā atrodas šāda piramīda, šķiet lielāka, un gaiss ir caurspīdīgāks. Sapņi labāk paliek atmiņā. Ir arī zināms, ka zelta attiecība tika plaši izmantota arhitektūrā un tēlniecībā. Tā piemērs bija Panteons un Partenons Grieķijā, arhitektu Bažeņova un Malēviča ēkas

8. Secinājums.

Jāsaka, ka zelta attiecībai ir liela nozīme mūsu dzīvē.

Ir pierādīts, ka cilvēka ķermenis tiek sadalīts zelta proporcijā ar jostas līniju.

Nautilus apvalks ir savīti kā zelta spirāle.

Pateicoties zelta attiecībai, starp Marsu un Jupiteru tika atklāta asteroīda josta - atbilstoši proporcijai vajadzētu būt citai planētai.

Virknes ierosināšana vietā, kas to sadala attiecībā pret zelta sadalījumu, neradīs virknes vibrāciju, tas ir, tas ir kompensācijas punkts.

Lidmašīnās ar elektromagnētiskiem enerģijas avotiem tiek izveidotas taisnstūrveida šūnas ar zeltainu attiecību.

La Gioconda ir veidota uz zelta trīsstūriem, zelta spirāle atrodas Rafaela gleznā "Zīdaiņu sišana".

Proporcija, kas atrasta Sandro Botticelli gleznā "Venēras dzimšana"

Ir daudz arhitektūras pieminekļu, kas būvēti, izmantojot zelta proporciju, ieskaitot Panteonu un Partenonu Atēnās, arhitektu Bažeņova un Malēviča ēkas.

Džons Keplers, kurš dzīvoja pirms pieciem gadsimtiem, sacīja: "Ģeometrijai ir divi lieliski dārgumi. Pirmais ir Pitagora teorēma, otrais ir segmenta sadalījums galējā un vidējā attiecībās."

Atsauču saraksts

1.D Pidvova. Ģeometrija un māksla. - M .: Mir, 1979. gads.

2. Žurnāls "Science and Technology"

3. Žurnāls "Kvant", 1973, 8. nr.

4. Žurnāls "Matemātika skolā", 1994, Nr. 2; 3. numurs.

5. Kovaļevs F.V. Zelta attiecība glezniecībā. K .: Vyscha skola, 1989. gads.

6. Stakhov A. Zelta koeficienta kodi.

7.Vorobjovs N.N. "Fibonači skaitļi" - Maskava: Zinātne 1964

8. "Matemātika - enciklopēdija bērniem" M .: Avanta +, 1998

9. Informācija no interneta.

Fibonači matricas un tā saucamās "zelta" matricas, jauna datora aritmētika, jauna kodēšanas teorija un jauna kriptogrāfijas teorija. Jaunās zinātnes būtība pārskatīšanā no visas matemātikas zelta attiecības viedokļa, sākot ar Pitagorsu, kas, protams, teorijā radīs jaunus un, iespējams, ļoti interesantus matemātiskos rezultātus. Praktiski - "zelta" datorizācija. Un tā kā ...

Neietekmēs šo rezultātu. Zelta koeficienta pamatā ir 4. un 6. rekursīvo attiecību invariants. Tā ir zelta proporcijas “stabilitāte”, kas ir viens no dzīvo matēriju organizācijas principiem. Arī zelta proporcijas pamatā ir divu eksotisku rekursīvu secību risinājums (4. att.) 4 rekursīvas Fibonači secības ...

Auss ir j5, un attālums no auss līdz vainagam ir j6. Tādējādi šajā statujā mēs redzam ģeometrisko progresiju ar saucēju j: 1, j, j2, j3, j4, j5, j6. (9. att.). Tādējādi zelta attiecība ir viens no senās Grieķijas mākslas pamatprincipiem. Sirds un smadzeņu ritmi. Cilvēka sirds pukst vienmērīgi - miera stāvoklī apmēram 60 sitieni minūtē. Sirds saspiež kā virzulis ...