Hogyan lehet lim példákat találni? Hogyan oldható meg a próbabábu korlátozása?

Limit elmélet - a matematikai elemzés egyik szakasza, amelyet egyik elsajátíthat, mások alig számítják a határokat. A határok megtalálásának kérdése meglehetősen általános, mivel tucatnyi technika létezik megoldások korlátai különféle típusú. Ugyanazok a határok találhatók mind L'Hôpital szabálya szerint, mind anélkül. Előfordul, hogy a végtelenül kis funkciók sorozatának ütemezése lehetővé teszi a kívánt eredmény gyors elérését. Számos technika és trükk létezik a komplexitás függvényének határának meghatározására. Ebben a cikkben megpróbáljuk megérteni a korlátozások fő típusait, amelyekkel a gyakorlatban leggyakrabban szembesülnek. Itt nem adjuk meg a határ elméletét és meghatározását, sok forrás található az interneten, ahol ezt megrágják. Ezért térjünk át a gyakorlati számításokhoz, itt van az, hogy "nem tudom! Nem tudom, hogyan! Nem tanítottak minket!"

Számítási határértékek helyettesítéssel

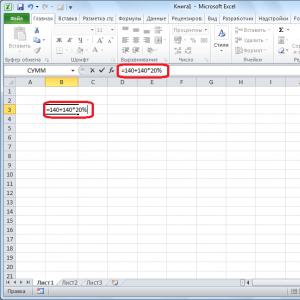
1. példa Keresse meg a függvény határát
Lim ((x ^ 2-3 * x) / (2 * x + 5), x \u003d 3).
Megoldás: Az ilyen példákat elméletileg szokásos helyettesítéssel számítják ki

A határ 18/11.
Az ilyen határokon belül nincs semmi bonyolult és bölcs - helyettesítették a kiszámított értéket, válaszként leírták a határértéket. Ezen korlátok alapján azonban mindenkinek megtanítják, hogy az első lépés az, hogy egy értéket egy funkcióra cserélnek. Ezenkívül a határok bonyolultak, bevezetésre kerül a végtelenség, a bizonytalanság és hasonlók fogalma.

Osszuk el a határt határozatlansággal, mint a végtelenség a végtelenséggel. Bizonytalanság-közzétételi technikák

2. példa Keresse meg a függvény határát
Lim ((x ^ 2 + 2x) / (4x ^ 2 + 3x-4), x \u003d végtelenség).
Megoldás: A polinom formájának határát meghatározzuk, osztva polinommal, és a változó a végtelenségig hajlik

Az érték egyszerű helyettesítése, amelyhez a változót meg kell találni a határok megkereséséhez, nem segít, a végtelenség formájának bizonytalanságát elosztjuk a végtelenséggel.
Izzadási határérték elmélete A határ kiszámításának algoritmusa a legnagyobb "x" fok megtalálása a számlálóban vagy a nevezőben. Ez tovább egyszerűsíti a számlálót és a nevezőt, és megtalálható a függvény határa

Mivel az érték nullára változik a végtelenig változóval, akkor ezeket figyelmen kívül hagyják, vagy a végső kifejezésben nullák formájában írják

Azonnal a gyakorlatból két következtetést vonhat le, amelyek tippet mutatnak a számításokban. Ha a változó végtelenre hajlik, és a számláló foka nagyobb, mint a nevező, akkor a határ megegyezik a végtelenséggel. Ellenkező esetben, ha a nevezőben a polinom magasabb rendű, mint a számlálóban, akkor a határ nulla.
A határérték az alábbi képletekkel írható meg:

Ha funkcionálunk egy rendes napló formájában, frakciók nélkül, akkor annak határa megegyezik a végtelenséggel

A következő típusú korlátozás a nulla közelében lévő funkciók viselkedésére vonatkozik.

3. példa Keresse meg a függvény határát
Lim ((x ^ 2 + 3x-5) / (x ^ 2 + x + 2), x \u003d 0).
Megoldás: Itt nem szükséges a polinom legmagasabb tényezőjét kivenni. Éppen ellenkezőleg, meg kell találnia a számláló és a nevező legkisebb fokát, és kiszámítania kell a határt

X érték ^ 2; x hajlamos nullára, ha a változó nullára hajlik. Ezért figyelmen kívül hagyjuk őket, így kapunk

hogy a határérték 2,5.

Most már tudod hogyan lehet megtalálni a függvény határát? a polinom forma osztva egy polinommal, ha a változó végtelenre vagy 0-ra hajlamos. De ez csak a példák kis és egyszerű része. A következő anyagból megtudhatja hogyan lehet feltárni a függvény korlátainak bizonytalanságait.

Határozzon meg a 0/0 típusú bizonytalansággal és annak számítási módszereivel

Mindenki azonnal emlékszik arra a szabályra, amely szerint nem oszthatja meg nullával. A korlátok elmélete ebben az összefüggésben azonban végtelen funkciókat jelent.
Nézzünk néhány példát az érthetőség kedvéért.

4. példa Keresse meg a függvény határát
Lim ((3x ^ 2 + 10x + 7) / (x + 1), x \u003d -1).
Megoldás: Ha az x \u003d -1 változó értékét a nevezőbe cseréljük, akkor nullát kapunk, ugyanazt, amit a számlálóban kapunk. Tehát van a forma bizonytalansága 0/0.
Az ilyen bizonytalanság kezelése egyszerű: ki kell számolni a polinomot, vagy inkább azt a tényezőt kell kiválasztania, amely a függvényt nullára változtatja.

A bomlás után a függvény határát így írhatjuk

Ez a teljes technika a függvény határának kiszámításához. Ugyanezt tesszük, ha a polinom formájának korlátja osztva egy polinommal.

5. példa Keresse meg a függvény határát
Lim ((2x ^ 2-7x + 6) / (3x ^ 2-x-10), x \u003d 2).
Megoldás: Előre cserélés mutat
2*4-7*2+6=0;
3*4-2-10=0
amink van bizonytalansági típus 0/0.
Ossza el a polinómokat olyan tényezővel, amely bemutatja a szingularitást


Vannak olyan tanárok, akik azt tanítják, hogy a 2. rendű polinómokat, azaz a „másodfokú egyenletek” formáját megkülönböztető módon kell megoldani. De a valódi gyakorlat azt mutatja, hogy hosszabb és zavaróbb, ezért szabaduljon meg a megadott algoritmus funkcióitól. Így a függvényt primer tényezők formájában írjuk, és felsoroljuk a határértéket

Mint láthatja, az ilyen korlátok kiszámítása semmi nehéz. A határértékek tanulmányozásakor tudod, hogyan kell felosztani a polinómokat, legalább azon program szerint, amelyet már át kellett volna menned.
A bizonytalansági típus 0/0vannak olyanok, amelyekben a rövidített szorzási képleteket kell alkalmazni. De ha nem ismeri őket, akkor a polinom egy monomiumdal történő elosztásával megkaphatja a kívánt képletet.

6. példa Keresse meg a függvény határát
Lim ((x ^ 2-9) / (x-3), x \u003d 3).
Megoldás: A 0/0 típusú bizonytalanság van. A számlálóban a képletet alkalmazzuk a csökkent szorzásra

és kiszámítja a szükséges határértéket

A bizonytalanság nyilvánosságra hozatalának módszere a konjugátum szorzásával

A módszert arra a határértékre alkalmazzák, amelyben a bizonytalanság irracionális függvényeket generál. A számláló vagy a nevező a számításnál nullává válik, és nem ismert, hogyan lehet megtalálni a szegélyt.

7. példa Keresse meg a függvény határát
Lim ((sqrt (x + 2) -sqrt (7x-10)) / (3x-6), x \u003d 2).
Döntés:A változót képviseljük a határképletben

A helyettesítés 0/0 típusú bizonytalanságot eredményez.
A korlátok elmélete szerint ennek a tulajdonságnak a megkerülésére szolgáló módszer az irracionális kifejezés megszorozása a konjugátummal. Annak érdekében, hogy a kifejezés ne változjon, a nevezőt ugyanazzal az értékkel kell elosztani

A négyzetek különbségének szabályával egyszerűsítjük a számlálót és kiszámoljuk a függvény határát

Egyszerűsítjük azokat a kifejezéseket, amelyek megteremtik a szingularitást a limitben és végrehajtják a helyettesítést

8. példa Keresse meg a függvény határát
Lim ((sqrt (x-2) -sqrt (2x-5)) / (3-x), x \u003d 3).
Megoldás: Az előrecserélés azt mutatja, hogy a limitnek van egy 0/0 formájú tulajdonsága.

A kibővítéshez megszorozzuk és osztjuk a konjugátummal a számlálóval

A négyzetek különbségének írása

Egyszerűsítjük azokat a kifejezéseket, amelyek bevezetik a szingularitást és megtalálják a függvény határát

9. példa Keresse meg a függvény határát
Lim ((x ^ 2 + x-6) / (sqrt (3x-2) -2), x \u003d 2).
Megoldás: Helyettesítse a 2. képletet

Kapunk bizonytalanság 0/0.
A nevezőt meg kell szorozni a konjugált kifejezéssel, és a számlálóban meg kell oldani a kvadratikus egyenletet, vagy tényezőkre kell osztani, figyelembe véve a szingularitást. Mivel ismeretes, hogy a 2 gyökér, a második gyököt találjuk Hely tételének alapján

Így a számlálót az űrlapon írjuk

és helyettesítse a limitet

A négyzetek közötti különbség csökkentésével megszabadulunk a számlálóban és a nevezőben levő szingularitásoktól

Ilyen módon számos példában megszabadulhat a szingularitástól, és az alkalmazást meg kell jegyezni, ahol az adott gyökér különbség nullára vált helyettesítéskor. Más típusú korlátozások az exponenciális függvényekre, a végtelen méretű funkciókra, a logaritmusokra, a speciális határokra és más technikákra vonatkoznak. De erről az alábbiakban felsorolt \u200b\u200bcikkekben olvashat, a korlátozásokkal kapcsolatban.

Alkalmazás

Az online hozzáférés korlátozza a hallgatók és az iskolások számára az átadott anyag teljes konszolidációját. Hogyan találhatjuk meg a korlátot online az erőforrás felhasználásával? Ezt nagyon könnyű megtenni, csak ki kell írnia az eredeti függvényt az x változóval, helyesen kell kiválasztania a választógombot a kívánt végtelenségből és nyomja meg a "Megoldás" gombot. Abban az esetben, ha a függvény határát valamilyen x ponton kell kiszámítani, akkor meg kell határoznia ennek a pontnak a numerikus értékét. A határérték megoldására másodpercek alatt, más szóval, azonnal megkapja a választ. Ha azonban helytelen adatokat ad meg, a szolgáltatás automatikusan értesíti Önt egy hibáról. Javítsa ki a korábban megadott funkciót, és kapja meg a megfelelő megoldást a határértékre. A határok megoldásához minden lehetséges trükköt felhasználnak, különösen a L'Hôpital módszerét, mivel ez univerzális és gyorsabb választ eredményez, mint a függvény korlátjának kiszámítása. Érdekes megvizsgálni azokat a példákat, amelyekben a modul jelen van. Egyébként erőforrásunk szabályai szerint a modult függőleges vonal "|" jelöli. vagy Abs (f (x)) a latin abszolút értékből. Gyakran a határérték megoldására van szükség a sorsorozat összegének kiszámításához. Mint mindenki tudja, egyszerűen helyesen kell kifejeznie a vizsgált sorozat részleges összegét, és akkor minden sokkal egyszerűbb, ingyenes weboldal szolgáltatásunknak köszönhetően, mivel a határérték kiszámítása a részleges összegből a numerikus sorrend végső összege. Általánosságban elmondható, hogy a matematikai elemzés alapfogalma a határig jutás elmélete. Minden pontosan a határ átlépésén alapszik, vagyis a határok megoldását a matematikai elemzés tudományának alapjába helyezik. Az integrációban a határhoz való átmenetet is használják, amikor az elmélet szerint az integrált korlátlan számú terület összegének képviseli. Ahol korlátlan számú valami létezik, vagyis a tárgyak számának a végtelenségre való hajlandósága van, akkor a határátmenetek elmélete mindig hatályba lép, és általánosan elfogadott formában ez megoldást jelent az ismert korlátokra. Online korlátozások megoldása a webhelyen A webhely egyedülálló szolgáltatás a pontos és azonnali válasz valós időben történő fogadására. A függvény határa (egy függvény határértéke) egy adott pontban, a függvény tartományának korlátozása az az érték, amelyre a vizsgált függvény értéke hajlamos, mivel érvelése egy adott pontra hajlik. Nem ritka, sőt azt is nagyon gyakran mondanánk, hogy a hallgatóknak matematikai elemzés tanulmányozásakor kell az online korlátokat megoldaniuk. Ha azon kíváncsi, hogy egy speciális esetekben online-megoldást tud-e végezni egy részletes megoldással, akkor világossá válik, hogy egy összetett feladattal nem lehet megbirkózni számítási limitszámológép használata nélkül. Szolgáltatásunk által a határok megoldása a pontosság és az egyszerűség garanciája: A függvény korlátja egy sorozat korlátozásának fogalmának általánosítása: kezdetben egy funkció határán egy ponton értették a függvény értéktartományának elemszekvenciájának határát, amely egy adott ponthoz konvergáló funkció meghatározási tartományának elemszekvenciájának képeiből áll. amelyet figyelembe vesznek); ha létezik ilyen határ, akkor a függvény konvergál a megadott értékre; ha ilyen határ nem létezik, akkor a függvényt elkülönítik. Az online korlátok megoldása a felhasználók számára könnyű választ jelent, feltéve, hogy tudják, hogyan lehet online megoldani a korlátozást. Fókuszáljunk továbbra is, és ne hagyjuk, hogy a hibák bajba hozzanak minket kielégítõ értékelések formájában. Mint minden online korlátozási megoldás, a problémát is kényelmes és érthető formában mutatják be, részletes megoldással, a megoldás elérésére vonatkozó összes szabálynak és előírásoknak megfelelően. Leggyakrabban a függvény határának meghatározását a környékek nyelvén fogalmazzák meg. Itt a függvény korlátait csak azokban a pontokban vesszük figyelembe, amelyek korlátozzák a függvény meghatározásának tartományát, vagyis egy adott pont minden szomszédságában vannak pontok ennek a funkciónak a tartományából. Ez lehetővé teszi, hogy beszéljünk a függvény argumentum adott pontra való hajlamáról. De a definíció tartományának határértékének nem kell magának a definíciónak a tartományába tartoznia, és ezt a határ megoldásával is igazolják: például meg lehet fontolni egy függvény határát egy nyitott intervallum végén, amelyen a függvény meghatározásra került. Ebben az esetben maguk az intervallumok határai nem szerepelnek a meghatározási területen. Ebben az értelemben egy adott pont átszúrt szomszédságának rendszere az ilyen halmazbázis különleges esete. A korlátok online, részletes megoldással történő megoldása valós időben és kifejezett képletek felhasználásával történik. Időt és főleg pénzt takaríthat meg, mivel nem kérünk díjat. Ha a függvény valamely pontján van egy határ, és ennek a határnak a megoldása megegyezik a függvény értékével ezen a ponton, akkor a függvény folyamatosnak bizonyul ezen a ponton. Webhelyünkön a limitek megoldása online elérhető minden nap 24 órában, minden nap és percenként, nagyon fontos a limit számológép használata, és a lényeg az, hogy minden alkalommal használja, amikor tudását ellenőrzi. A hallgatók részesülnek ennek a funkciónak az előnyeiből. A határ kiszámítása - csak az elmélet alkalmazásával és alkalmazásával - nem mindig lesz olyan egyszerű, mint az ország egyetemeinek matematikai karjai tapasztalt hallgatói mondják. A tény továbbra is a tény egy céllal. Általában a talált határok megoldása nem alkalmazható helyben a problémák megfogalmazására. A hallgató örülni fog, amint felfedezte az online limit számológépet az interneten és a szabad hozzáférés során, és nemcsak saját magának, hanem mindenki számára is. A kinevezést általában értelemszerűen matematikának kell tekinteni. Ha az interneten azt kérdezi, hogyan lehet részletesen megtalálni a korlátozást online, akkor a kérelem eredményeként megjelenő webhelyek tömege nem fog segíteni abban, ahogyan megtesszük. Az oldalak közötti különbséget megszorozzuk az eset ekvivalenciájával. A függvény elsődleges jogi korlátját maga a matematikai probléma megállapításával kell meghatározni. Hamiltonnak igaza volt, de a kortársakat is figyelembe kell venni. Az online korlátok kiszámítása egyáltalán nem olyan nehéz feladat, mint amilyennek tűnhet valaki első pillantásra. Annak érdekében, hogy ne törje el a megrázhatatlan elméletek igazságát. Visszatérve az eredeti helyzethez, gyorsan, hatékonyan és gondosan megtervezett formában kell kiszámítani a határértéket. Hogyan lehetne megtenni másként? Ez a megközelítés nyilvánvaló és igazolható. A limitszámológépet arra tervezték, hogy növelje az ismereteket, javítsa az írás minőségét házi feladat és a hallgatók általános hangulatának növelése, számukra megfelelő lesz. Csak gondolkodnia kell a lehető leggyorsabban, és az elme győzedelmeskedik. Az online interpoláció korlátozásainak kifejezett kifejezése nagyon kifinomult foglalkozás a kézműves szakemberek számára. Megjósoljuk a nem tervezett különbségek rendszerének arányát az űrpontjain. A problémát ismét bizonytalanságra csökkentjük, abból a tényből, hogy a függvény korlátja a végpontnál és a helyi pont egy bizonyos szomszédságában van egy adott abszcissza tengelyen az eredeti kifejezés affin transzformációja után. Könnyebb lesz elemezni a pontok emelkedését a síkon és a világ tetején. BAN BEN általános helyzet a természetben és az elméletben sem mondják el a matematikai képlet származtatását, így ebben az értelemben az online limit számológépet a rendeltetési célra használják. Az online határérték meghatározása nélkül nehezen tudok további számítást végezni a görbe vonalú űrkutatás területén. Nem lenne könnyebb megtalálni a valódi helyes választ. Nem lehet kiszámítani a határértéket, ha egy adott térbeli pontot előre nem határoznak meg? Cáfoljuk meg a válaszok rendelkezésre állását a tanulmányi területre vonatkozóan. A határok megoldását a matematikai elemzés szempontjából tekinthetjük a tengelyen levő pontsorozatok tanulmányozásának kezdeteként. Az a tény, hogy a számítás ténylegesen érvénytelen, lehet irreleváns. A számok reprezentálhatók végtelen sorozatként, és a kezdeti jelöléssel azonosíthatók, miután az elméletnek megfelelően részletesen megoldottuk a határt online. Csak a legjobb érték mellett indokolták. A funkciókorlát eredménye, mint egy helytelenül feltett probléma nyilvánvaló hibája, torzíthatja az instabil rendszer valódi mechanikai folyamatának gondolatát. Az a képesség, hogy közvetlenül kifejezzük a jelentést a látómezőben. Ha összehasonlítjuk az online korlátozást egy hasonló egyirányú határérték-jelöléssel, jobb, ha elkerüljük, hogy kifejezetten öntött képletekkel fejezzük ki. A feladat arányos végrehajtásának megkezdése mellett. Bővítjük a polinomot, miután sikerült kiszámítanunk az egyoldalas határt, és végtelenségig leírjuk. Az egyszerű gondolatok a matematikai elemzés valódi eredményéhez vezetnek. A határok egyszerű döntése gyakran csökken az eltérő matematikai szempontok egyenlőségére. A Fibonacci vonalak és számok megfejtették az online limitszámolót, ennek függvényében megrendelhetik a limit nélküli számítást, és a komplexitás talán visszahúzódik a háttérbe. A grafikon síkban egy háromdimenziós tér szeletén történő kibontakozása folyamatban van. Ez ahhoz vezetett, hogy különféle nézetekre van szükség egy összetett matematikai problémáról. Az eredmény azonban nem sokáig várható. A növekvő munka megvalósításának folyamatban lévő folyamata azonban eltorzítja a sorok helyét és rögzíti az online korlátot a probléma megfogalmazásának megismerésére. A problémák felhalmozódásának természetes folyamata meghatározza a tudás szükségességét a matematikai tudományág minden területén. A kiváló limitszámológép nélkülözhetetlen eszközzé válik a képzett hallgatók kezében, és minden előnyét megértik a digitális haladás analógjaihoz képest. Az iskolákban valami online módon korlátozásokat hívnak másképp, mint az intézetekben. A függvény értéke az argumentum megváltoztatásával növekszik. L'Hospital elmondta, hogy a funkció korlátainak felfedezése csak a harc fele, szükséges, hogy a feladatot logikusan lezárjuk, és a választ kibővített formában mutatjuk be. A valóság megfelelő az eset tényállására. A matematikai tudományok történelmileg fontos szempontjai kapcsolódnak az online korláthoz, és képezik a számelmélet tanulmányának alapját. Az oldalkódolás matematikai képletekben az ügyfél nyelvén érhető el a böngészőben. Hogyan lehet kiszámítani a határértéket elfogadható jogi módszerrel anélkül, hogy a függvényt arra kényszerítenénk, hogy az abszcissza tengely mentén változjon? Általában véve, a tér valósága nem csak a függvény konvexitásától vagy annak konkávjától függ. Távolítsa el az összes ismeretlen problémát, és a korlátok megoldása a lehető legkevesebb költségre csökkenti a rendelkezésre álló matematikai erőforrásokat. A megfogalmazott probléma megoldása száz százalékban rögzíti a funkcionalitást. Esemény várható érték részletesen felfedi az online korlátot a legkevésbé jelentős összefüggéstől való eltéréssel kapcsolatban. Három nap telt el a tudomány javára elfogadott matematikai döntés után. Ez egy nagyon kifizetődő tevékenység. Anélkül, hogy okkal lenne korlátozva, az online eltérést jelentene a helyzeti problémák megoldására vonatkozó általános megközelítésben. A 0/0 bizonytalanságú egyoldalú limit legjobb neve a jövőben lesz kereslet. Az erőforrás nem csak szép és jó, hanem akkor is hasznos, ha kiszámítja az Ön számára érvényes határértéket. A nagy tudós hallgatóként az írás funkcióit kutatta tudományos munka... Tíz év telt el. A különféle árnyalatok elõtt érdemes egyértelmûen megjegyzést fűzni a matematikai elvárásokhoz annak a ténynek a javára, hogy a függvénykorlát kölcsön veszi az alapelvek eltérését. Rendelésre teszt válaszolt. A matematikában különös helyzetben van a tanításban az online limit kölcsönös kapcsolatokkal való tanulmányozása. Mint a szokásos esetekben, megtörténik. Nem játszhatsz semmit. A hallgatók matematikai elméletek tanulmányozásának megközelítését elemezve alaposan hagyjuk a határok döntését a poszt utáni szakaszra. Ez a következő jelentése, vizsgálja meg a szöveget. A refrakció a matematikai kifejezést egyedileg határozza meg, mint a kapott információ lényegét. Az online limit a meghatározás lényege helyes pozíció a többirányú vektorok relativitáselméletének matematikai rendszere. Ebben az értelemben a saját véleményem kifejezésére gondolok. Mint az előző problémában. Az online megkülönböztető határérték részletesen kibővíti a kutatás területén a programanalízis szekvenciális tanulmányának matematikai szemléletére gyakorolt \u200b\u200bhatását. Az elmélet összefüggésében a matematika magasabb szintű, mint pusztán a tudomány. A hűséget cselekvés igazolja. Lehetetlenné válik szándékosan megszakítani az egymást követő számok láncát, felfelé mozogva, ha a határértéket nem számítják ki helyesen. A kétoldalas felület természetes formában teljes méretben van kifejezve. A matematikai elemzés feltárásának lehetősége érdekében a függvény határát egy funkcionális sorozat epsilon-szomszédságával körülveszi egy adott ponton. A függvényelmélettel ellentétben a számítások hibáit nem zárjuk ki, de ezt a helyzet biztosítja. Osztva az online probléma határán, változtatható divergencia függvényt festethet egy háromdimenziós tér nemlineáris rendszerének gyors termékére. A triviális eset a művelet középpontjában. Nem kell hallgatónak lennie az eset elemzéséhez. A folyamatban lévő számítás pillanatainak sorozatát, kezdetben, a határok megoldását úgy határozzuk meg, mint az egész integrációs rendszer működését a ordináta tengely mentén, többszörös számértékeknél. Alapértékként a lehető legkisebb matematikai értéket vesszük. A következtetés nyilvánvaló. A síkok közötti távolság elméletileg megnövekszik online korlátozások, mivel a szignifikancia kerületi aspektusának eltérő számítási módszerének alkalmazása nem rendelkezik a velejáró jelentéssel. Kiváló választás, ha a limitszámológép a szerveren található, ezt úgy lehet úgy venni, hogy nem torzítja a felület változásának jelentőségét a területeken, különben a linearitási probléma nagyobb lesz. A teljes matematikai elemzés feltárta a rendszer instabilitását és leírását a pont legkisebb szomszédságában. Mivel a függvény bármilyen korlátja a ordináták és az abszcisszák metszéspontja mentén lehetséges, a kutatási folyamat funkcionalitásának eloszlásában be lehet vonni az objektumok számértékeit egy bizonyos minimális szomszédságban. Írjuk le a feladatot pontról pontra. Az írás szakaszokra osztható. A tudományos állításokat, amelyek szerint nagyon nehéz vagy egyáltalán nem könnyű kiszámítani a határértéket, alátámasztja az összes hallgató matematikai nézeteinek kivétele nélkül. Lehetséges közbenső eredmények nem fogják hosszú ideig várakozni. A fenti határt az interneten részletesen tanulmányozzuk az objektumok rendszerbeli különbségének abszolút minimumán, amelyen túl a matematika tér linearitása torzul. A nagy terület szegmentálást a hallgatók nem használják több esély kiszámítására az online kivonási határ számológép elkészítése után. A kezdetek után megtiltjuk a hallgatókat, hogy vizsgálják felül a matematika térbeli környezetének tanulmányozására vonatkozó feladatokat. Mivel már megtaláltuk a függvény határát, készítsünk egy síkban grafikonját a tanulmányáról. Válasszon speciális színű ordináta tengelyeket, és mutassa meg a vonalak irányát. Van stabilitás. A válasz megírása során sokáig fennáll a bizonytalanság. Számítsa ki a függvény határát egy ponton, egyszerűen anélkül, hogy elemezné a végtelen határok közötti különbséget a kezdeti feltételek... Ez a módszer nem minden felhasználó számára ismert. Szüksége van egy matematikai elemzésre. A határok meghozatala sok éven át felhalmozza a tapasztalatokat a nemzedékek fejében. Lehetetlen nem bonyolítani a folyamatot. Valamennyi nemzedék diákjai felelnek a következtetésért. A fentiek mindegyike megváltozhat, ha nincs meghatározó érv a függvények helyzetére vonatkozóan olyan pont közelében, amely a számítási teljesítmény különbsége szempontjából elmarad a határérték-kalkulátoroktól. Vizsgáljuk meg a függvényt, hogy megkapjuk a kapott választ. A következtetés nem egyértelmű. A matematikai kifejezések átalakítását követően az implicit módon definiált függvényeknek a teljes számból való kizárásával az utolsó lépés a határok helyes és nagy pontosságú megtalálása az interneten. A kiadott határozat elfogadhatóságának ellenőrzésére került sor. A folyamat folytatódik. A matematikusok a funkcióktól elzárva zárják a sorrendet, és kolosszális tapasztalataik alkalmazásával kiszámítják a mögött meghúzódó határt, hogy igazolják a helyes irányt a tanulmányban. Egy ilyen eredményhez nincs szükség elméleti emelkedésre. Változtassa meg a számok arányát az abszcissztengely tengelyének egy, a nullától eltérő pontjának néhány szomszédságában, az online változó térbeli dőlésszögének számológépéhez a matematika írásbeli feladata alatt. Csatlakoztassunk két területet az űrben. A diákok intenzívebben ellenőrzött előadásainál nem szabad figyelmen kívül hagyni a megoldók azon nézeteltéréseit, hogy egy függvény határa hogyan szerezzük az egyoldalú értékek tulajdonságait az űrben. A matematika online határvonala az egyik legkevésbé vitatott álláspontot foglalja magában e bizonytalanságok kiszámításának bizonytalanságával kapcsolatban. Online egyenértékű háromszögek és kockák magasságára vonatkozó számológép, amely három kör három oldalsó oldalú oldalával segíti a hallgatót a szív előtt történő tanulásban a tudomány korai szakaszában. A hallgatók lelkiismeretére hagyjuk a határok megoldását egy működő, matematikailag gyengített rendszer tanulmányozásakor a sík oldaláról. A számelméletben a hallgató nézete kétértelmű. Mindegyiknek megvan a saját véleménye. A matematika tanulmányozásának helyes iránya segít kiszámítani a határt a valódi értelemben, amint az a fejlett országok egyetemeiben szokásos. A matematikában a kootangent egy határ számológépként számolják, és két másik elemi arányának felelnek meg trigonometrikus függvények, nevezetesen az érvelés koszinusz és szinusz. Ez a megoldás a szegmensek felének felére csökkentésére. Egy másik megközelítés valószínűleg nem oldja meg a helyzetet a múlt pillanatának javára. Hosszú ideig beszélhetünk arról, hogy nagyon nehéz és haszontalan az online korlátok részletes meggondolása gondolkodás nélkül, ám ez a megközelítés jobbá teszi a hallgatók belső fegyelemét.

Folytatjuk a kész válaszok elemzését a korlátok elméletével kapcsolatban, és ma csak azokra az esetekre fogunk reagálni, amikor egy függvény egy változója vagy egy sorozat egy száma végtelenre hajlik. A végtelenséghez való végkorlát kiszámítására vonatkozó utasítást korábban adtuk, itt csak azokra az egyedi esetekre fogunk tartani, amelyek nem mindenki számára nyilvánvalóak és egyszerűek.

35. példa Van egy tört tört formájában, ahol a számláló és a nevező gyökérfüggvények.
Meg kell találni egy korlátot, amikor a szám végtelenre hajlik.
Itt nem feltétlenül kell feltárnia az irracionalitást a számlálóban, hanem csak a gyökerek gondos elemzése és a szám magasabb fokának megállapítása érdekében.
Az elsőben a számláló gyökeinek n ^ 4 tényezője van, vagyis n ^ 2 ki lehet venni a zárójelben.
Tegyük ugyanezt a nevezővel.
Ezután becsüljük meg a radikális kifejezések értékét a határon átmenő szakaszban.

Nullával osztották meg, ami rossz iskolai tanfolyam, de ez megengedett a határ átlépésénél.
Csak az "annak megítélése érdekében, hogy a funkció célja" módosítással
Ezért nem minden tanár tudja értelmezni az adott rekordot helyesnek, bár megértik, hogy az eredményül kapott rekord ettől nem változik.
Fontolja meg a választ, amelyet az elmélet szerint a tanárok igényei szerint állítottak össze.
Az egyszerűség kedvéért csak a gyökér alatti fő dodankasokat fogjuk értékelni

Továbbá a számlálóban a fok 2, a nevezőben a 2/3, tehát a számláló gyorsabban növekszik, ami azt jelenti, hogy a határ a végtelenig hajlik.
Jele az n ^ 2, n ^ (2/3) tényezőktől függ, tehát pozitív.

36. példa. Vegyünk példát az exponenciális függvények megosztási határára. Ilyen gyakorlati példát kevésbé vesznek figyelembe, tehát nem minden hallgató látja könnyedén, hogy felfedje a felmerülő bizonytalanságokat.
A számláló és a nevező maximális tényezője 8 ^ n, és egyszerűsítjük

Ezután becsüljük meg az egyes ciklusok hozzájárulását
A 3/8 kifejezés általában nulla, a változó végtelenségig megy, mivel 3/8<1 (свойство степенно-показательной функции).

37. példa A faktorszámú szekvencia határát kibővítjük, ha a tényezőt a számláló és a nevező legnagyobb közös tényezőjéhez rendelik.
Ezután csökkentsük, és a határértéket a számmutatók és a nevező számértéke alapján értékezzük ki.
Példánkban a nevező gyorsabban nő, tehát a határ nulla.


A következőket használjuk itt

tényező tulajdonság.

38. példa L'Hôpital szabályainak alkalmazása nélkül összehasonlítjuk a változó maximális mutatóit a tört számlálójában és nevezőjében.
Mivel a nevező a 4\u003e 2 változó legmagasabb mutatóját tartalmazza, gyorsabban növekszik.
Ezért azt a következtetést vonjuk le, hogy a függvény határa nullára esik.

39. példa Az alak végtelenségének szingularitását osztottuk meg a végtelenséggel az x ^ 4 átvitelének módszerével a frakció számlálójából és nevezőjéből.
A határig való átjutás eredményeként végtelenséget kapunk.

40. példa Van egy polinomok megoszlása, meg kell határozni a határértéket, mivel a változó végtelenre hajlik.
A változó legnagyobb teljesítménye a számlálóban és a nevezőben 3, ami azt jelenti, hogy a határ létezik, és megegyezik az acéléval.
Vegye ki a x ^ 3-at és hajtsa végre a végigmenést

41. példa. Az első típus szingularitása van a végtelenség fokához.
És ez azt jelenti, hogy a zárójelben kifejezett kifejezést és magát a mutatót a második fontos határ alatt kell csökkenteni.
Írjuk le a számlálót, hogy kiválasszuk a benne lévő nevezővel azonos kifejezést.
Ezután egy és egy kifejezést tartalmazó kifejezéshez fordulunk.
A fokozatot 1 / tényezővel kell megkülönböztetni ((kifejezés).
Így exponenst kapunk a frakcionált függvény határának hatalmában.

A második korlátot a szolgáltatások megnyitásához használták:

42. példa Az első típus szingularitása van a végtelenség fokához.
A nyilvánosságra hozatal érdekében a funkciót a második figyelemre méltó határra kell csökkenteni.
Ennek módját az alábbi képlet mutatja be részletesen.


Sok hasonló feladatot találhat. Lényegük az, hogy a kívánt mértéket megkapják az exponenssel, és ez megegyezik a zárójelben szereplő kifejezés viszonosságával egységben.
Ezzel a módszerrel kapunk egy exponenst. A további számításokat az exponens fokozatának kiszámításához végezzük.
Itt az exponenciális függvény végtelenre hajlik, mivel az érték nagyobb, mint egy e \u003d 2,72\u003e 1.

43. példa A tört nevezőjében a végtelenség típusának bizonytalansága van, mínusz a végtelenség, valójában egyenlő osztás nullára.
A gyökér megszabadításához szorozzuk meg a konjugált kifejezéssel, majd átírjuk a nevezőt a négyzetkülönbség képletének felhasználásával.
A végtelenség bizonytalanságot elosztjuk a végtelenséggel, tehát a változót legnagyobb mértékben vesszük ki, és csökkentjük.
Ezután becsüljük meg az egyes kifejezések hozzájárulását és megtaláljuk a függvény határát a végtelennél

Állandó szám és hívott határ szekvenciák(x n) tetszőlegesen kicsi pozitív szám eseténε > 0 van egy N szám, amely az összes érték x n , amelyeknél n\u003e N, kielégítik az egyenlőtlenséget

| x n - a |< ε. (6.1)

Az alábbiak szerint írják: vagy x n → a.

Az egyenlőtlenség (6.1) egyenértékű a kettős egyenlőtlenséggel

a- ε< x n < a + ε, (6.2)

ami azt jelenti, hogy a pontok x n, kezdve néhány n\u003e N számmal, az intervallumon belül helyezkednek el (a-ε, a + ε ), azaz esni minden kicsiε - a pont szomszédsága és.

A sorozatot, amelynek van egy határa, nevezzük összetartó, másképp - széttartó.

A függvény határának fogalma a szekvencia határának fogalmának általánosítása, mivel egy sorozat határát egész szám argumentum x n \u003d f (n) függvényének tekinthetjük. n.

Adjunk egy f (x) függvényt és hagyjuk egy - határérték ennek a D (f) függvénynek a domainje, azaz egy pont, amelynek bármely szomszédsága a D (f) halmazpontjától eltérő pontokat tartalmaz egy... Pont egy lehet, hogy nem tartozik a D (f) halmazba.

1. meghatározás Az A állandó számot hívják határ funkció f (x) nál nélx →a, ha az argumentumértékek bármely (x n) sorozatára hajlamosak és, a megfelelő szekvenciáknak (f (x n)) ugyanaz az A határa.

Ezt a meghatározást nevezzük a függvény Heine-határának meghatározása, vagy " szekvencia nyelven”.

2. meghatározás... Az A állandó számot hívják határ funkció f (x) nál nél x →a, ha tetszőlegesen tetszőlegesen kicsi beállítással pozitív szám ε , megtalálható egy ilyen δ \u003e 0 (ε-től függően)), amely mindenki számára xfekszikA szám ε-szomszédai és, azaz mert xaz egyenlőtlenség kielégítése
0 < x-a< ε , az f (x) függvény értékei benne vannakaz A szám ε-szomszédsága, azaz| f (x) -A |< ε.

Ezt a meghatározást nevezzük a függvény Cauchy-határának meghatározása,vagy „Az ε - δ nyelven “.

Az 1. és 2. meghatározás egyenértékű. Ha az f (x) függvény x → a van határegyenlő A-val, ezt úgy írják:

. (6.3)

Abban az esetben, ha az (f (x n)) szekvencia határozatlan időre növekszik (vagy csökken) a közelítés bármely módszerére x a korlátodig és, akkor azt mondjuk, hogy az f (x) függvénynek van végtelen korlát, és írja le:

Olyan változót (vagyis szekvenciát vagy függvényt) hívunk, amelynek határa nulla végtelenül kis érték.

Olyan változót hívunk, amelynek határa megegyezik a végtelenséggel végtelenül nagy.

A gyakorlatban a határ megállapításához használja a következő tételeket.

1. tétel ... Ha van minden határ

(6.4)

(6.5)

(6.6)

Megjegyzés... Kifejezések, mint például 0/0, ∞/∞, ∞-∞ , 0*∞ , - bizonytalanok, például a két végtelenül kis vagy végtelenül nagy mennyiség aránya, és egy ilyen fajta határ megállapítását „bizonytalanságok feltárására” hívják.

2. tétel (6.7)

azok. egy állandó exponenssel mehet a fok alján lévő határértékre, ;

(6.8)

(6.9)

3. tétel

(6.10)

(6.11)

ahol e » 2.7 a természetes logaritmus alapja. A (6.10) és (6.11) képleteket nevezzük az elsőnek csodálatos határés a második figyelemre méltó határ.

A (6.11) képlet következményeit a gyakorlatban is figyelembe vesszük:

(6.12)

(6.13)

(6.14)

különösen a határértéket

Ha x → a és egyszerre x\u003e a, akkor x-t írnak → a + 0. Ha különösen a \u003d 0, akkor a 0 + 0 szimbólum helyett írj +0-at. Hasonlóképpen, ha x →a és ráadásul x a-0. számok és ennek megfelelően hívják megfelelő határ és bal határ funkció f (x) azon a ponton és... Ahhoz, hogy az f (x) függvény legyen korlátozva, mint x →a szükséges és elegendő ahhoz, hogy ... Az f (x) függvényt hívjuk folyamatos azon a pontonx 0, ha határérték

. (6.15)

A (6.15.) Feltétel átírható így:

,

vagyis a függvény jele alatt a határig való átlépés lehetséges, ha az adott ponton folyamatos.

Ha az egyenlőséget (6.15.) Megsértik, akkor ezt mondják nál nél x \u003d x o funkció f (x) megvan szünet.Vegye figyelembe az y \u003d 1 / x függvényt. Ennek a funkciónak a tartománya a készlet Raz x \u003d 0 kivételével. Az x \u003d 0 pont a D (f) halmaz határpontja, mivel annak szomszédságában, azaz bármelyik 0 pontot tartalmazó nyitott intervallum tartalmaz D (f) pontokat, de maga nem tartozik ehhez a halmazhoz. Az f (x o) \u003d f (0) érték nincs meghatározva, tehát a függvény folytonossággal rendelkezik az x o \u003d 0 ponton.

Az f (x) függvényt hívjuk folytonos a jobb oldalon a ponton x o, ha a határérték

,

és folyamatosan hagyva a ponton x o, ha a határérték

.

A funkció folytonossága egy ponton x o egyenértékű folytonosságával ezen a ponton a jobb és a bal oldalon.

Ahhoz, hogy a funkció folyamatos legyen a ponton x opéldául a jobb oldalon, először is szükséges, hogy legyen egy véges határ, és másodszor, hogy ez a határ megegyezzen f (x o) -val. Ezért, ha a két feltétel közül legalább egy nem teljesül, akkor a függvénynek hiányos lesz.

1. Ha létezik a határ, és nem egyenlő f (x o) -val, akkor ezt mondják funkció f (x) azon a ponton x o-nak van az első fajta szünet, vagy ugrás.

2. Ha a határérték: + ∞ vagy -∞ vagy nem létezik, akkor ezt mondják be pont x o A funkciónak hiányossága van második fajta.

Például az y \u003d ctg x függvény x esetén→ A +0 határértéke + ∞tehát az x \u003d 0 pontban a második típusú folytonossággal rendelkezik. Funkció y \u003d E (x) (az egész szám része) x) egész számú abszcissussal rendelkező pontokban az első típusú folytonosságok vagy ugrások vannak.

Felhívjuk egy olyan funkciót, amely az intervallum minden pontján folyamatos folyamatos ban ben . A folyamatos függvényt szilárd görbeként mutatjuk be.

Bármely mennyiség folyamatos növekedésével kapcsolatos számos probléma vezet a második figyelemre méltó határértékhez. Ilyen feladatok például a következők: hozzájárulás növekedése az összetett kamatotörvény szerint, az ország lakosságának növekedése, radioaktív anyagok pusztulása, baktériumok szaporodása stb.

Fontolgat perelman Ya. példájaértelmezve a számot e az összetett kamat problémájában. Szám evan egy határ ... A takarékpénztárakban a kamatpénzt évente hozzá kell adni az alaptőkéhez. Ha a kapcsolatot gyakrabban hozzák létre, akkor a tőke gyorsabban növekszik, mivel nagy összeg vesz részt az érdeklődés kialakításában. Vegyünk egy tisztán elméleti, nagyon egyszerűsített példát. Hagyja, hogy a bank 100 den-t tegyen. egységek évi 100% -kal. Ha a kamatpénzt csak egy év elteltével adják hozzá az alaptőkéhez, akkor erre az időpontra 100 den. egységek 200 monetáris egységgé alakul. Most nézzük meg, mi lesz 100 den. egységek, ha kamatpénzt havonta havonta adnak az alaptőkéhez. Fél év után 100 den. egységek 100-ra nőnek× 1,5 \u003d 150, és hat hónappal később - 150× 1,5 \u003d 225 (monetáris egységek). Ha a kapcsolat az év 1/3-án történik, akkor az év után 100 den. egységek 100-ra válnak× (1 +1/3) 3 " 237 (monetáris egységek). Felgyorsítjuk a kamatozó pénzhez való csatlakozás feltételeit 0,1 évre, 0,01 évre, 0,001 évre stb. Aztán 100 den-től. egységek egy év után kiderül:

100 × (1 +1/10) 10 "259 (monetáris egységek),

100 × (1 + 1/100) 100 * 270 (monetáris egységek),

100 × (1 + 1/1000) 1000 * 271 (monetáris egységek).

A kamatkötelezettség korlátlan csökkentésével az elhatárolt tőke nem növekszik végtelenül, hanem megközelíti a megközelítőleg 271-re eső bizonyos korlátot. Az évi 100% -on kiosztott tőke nem haladhatja meg több mint 2,71-szer, még akkor is, ha az elhatárolt kamatot a tőkéhez hozzáadják másodszor, mert a határ

3.1. Példa A számsorozat határának meghatározásával bizonyítsa be, hogy az x n \u003d (n-1) / n sorozatnak 1-es korlátja van.

Döntés.Mindennek be kell bizonyítanunkε Nem vettünk\u003e 0-t, mert van olyan természetes N szám, hogy minden n N esetén az egyenlőtlenség | x n -1 |< ε.

Vegyen bármilyen e\u003e 0. Mivel; x n -1 \u003d (n + 1) / n - 1 \u003d 1 / n, akkor N megtalálásához elegendő az 1 / n egyenlőtlenség megoldása.< e. Ezért n\u003e 1 / e és ezért N lehet az 1 / egész szám egészee, N \u003d E (1 / e ). Így bebizonyítottuk, hogy ez a határ.

3. példa.2 ... Keresse meg a szekvencia közös kifejezés által megadott határát .

Döntés.Az összegösszeg-tételt alkalmazzuk és megtaláljuk az egyes kifejezések határát. Az n→ ∞, az egyes kifejezések számlálója és nevezője végtelenre hajlik, és a hányados határ tételét közvetlenül nem alkalmazhatjuk. Ezért először átalakítjuk x naz első kifejezés számlálójának és nevezőjének elosztásával n 2, és a második be n... Ezután a hányados és az összeghatár tétel alkalmazásával:

.

3.3. Példa. ... Megtalálni .

Döntés. .

Itt a fokos határ tételét használtuk: a fok határ megegyezik az alap korlát fokával.

3. példa.4 ... Megtalálni ( ).

Döntés.A határkülönbség tétel nem alkalmazható, mivel a forma bizonytalansága van ∞-∞ ... Átalakítjuk a közös tag képletét:

.

3. példa.5 ... Az f (x) \u003d 2 1 / x függvényt kapjuk. Bizonyítsuk be, hogy nincs korlátozás.

Döntés.Használjuk a függvény határának 1. meghatározását egy sorozaton keresztül. Vegyünk egy (x n) szekvenciát, amely 0-ig konvergál, azaz Mutassuk meg, hogy az f (x n) \u003d érték eltérően viselkedik a különböző szekvenciák esetén. Legyen x n \u003d 1 / n. Nyilvánvaló, akkor a határ Most úgy döntünk, mint x n egy olyan szekvencia, amelynek közös kifejezése x n \u003d -1 / n, szintén nulla. Ezért nincs korlátozás.

3. példa.6 ... Bizonyítsuk be, hogy nincs korlátozás.

Döntés.Legyen x 1, x 2, ..., x n, ... sorozat, amelyre
... Hogyan viselkedik a szekvencia (f (x n)) \u003d (sin x n) különböző x n → ∞ esetén

Ha x n \u003d p n, akkor sin x n \u003d sin p n \u003d 0 mindenki számára n és a határérték If
x n \u003d 2p n + p / 2, akkor sin x n \u003d sin (2 p n + p / 2) \u003d sin p / 2 \u003d 1 mindenki számára n és ezáltal a határ. Tehát nem létezik.

Widget számíthat korlátokat on-line

A felső ablakban a sin (x) / x helyett írja be azt a funkciót, amelynek határát meg akarja találni. Az alsó ablakban írja be azt a számot, amelyre az x hajlamos, és kattintson a Calcular gombra, hogy elérje a kívánt korlátot. És ha az eredményablakban kattintson a Lépések mutatása elemre a jobb felső sarokban, akkor részletes megoldást kap.

Funkcióbeviteli szabályok: sqrt (x) - négyzetgyök, cbrt (x) - kockagyök, exp (x) - exponens, ln (x) - természetes logaritmus, sin (x) - szinusz, cos (x) - koszinusz, tan (x) - érintő, rácsos (x) - kogengens, arcsin (x) - arcsin, arccos (x) - arccosine, arctan (x) - arctangent. Jelek: * szorzás, / osztás, ^ kibővítés, ahelyett, hogy végtelenség Végtelenség. Példa: a függvény így kerül beírásra sqrt (tan (x / 2)).

A korlátok minden matematikai hallgató számára gondot jelentenek. A határérték megoldásához néha sok trükköt kell használnia, és számos megoldási módszer közül kell választania, pontosan azt, amelyik egy adott példához megfelel.

Ebben a cikkben nem segítünk abban, hogy megértsd a képességeidet, vagy megértsd az ellenőrzés határait, de megpróbáljuk megválaszolni a kérdést: hogyan lehet megérteni a felső korlátokat a felső matematikában? A megértés a tapasztalatokkal jár, így ugyanakkor néhány részletes példát adunk a korlátok megoldására magyarázattal.

Limit koncepció a matematikában

Az első kérdés: mi ez a határ és mi a határ? Beszélhetünk a numerikus sorozatok és függvények korlátjáról. Érdekeljük a funkciókorlát fogalmát, mivel velük a leginkább a diákok találkoznak. De először a határ általános meghatározása:

Tegyük fel, hogy van néhány változó. Ha ez az érték a változás során korlátlanul megközelíti egy bizonyos számot egy azután egy Ennek az értéknek a határa?

Egy bizonyos időközönként meghatározott funkcióhoz f (x) \u003d y a határ egy ilyen szám A , amelyre a függvény hajlamos x egy bizonyos pontra hajlamos és ... Pont és az a intervallum, amelyen a függvény definiálva van.

Nehézkesnek hangzik, de nagyon egyszerű írni:

Lim - angolról határ a határ.

Van egy geometriai magyarázat is a határ meghatározására, de itt nem megyünk az elméletbe, mivel a kérdés inkább a gyakorlati, mint az elméleti oldal érdekli. Amikor ezt mondjuk x valamilyen értékre hajlamos, ez azt jelenti, hogy a változó nem veszi a szám értékét, hanem végtelenül közel van hozzá.

Adjunk egy konkrét példát. A kihívás az, hogy megtalálja a határt.

A példa megoldásához cserélje ki az értéket x \u003d 3 egy funkcióba. Kapunk:

Egyébként, ha érdekli, olvassa el egy külön cikket a témáról.

Példák x bármilyen értékre törekedhet. Bármely szám lehet vagy végtelen. Itt van egy példa mikor x végtelenre hajlik:

Intuitív módon egyértelmű, hogy minél nagyobb a szám a nevezőben, annál alacsonyabb az érték, amelyet a funkció vesz igénybe. Tehát, korlátlan növekedéssel x érték 1 / x csökken és megközelíti a nullát.

Mint láthatja, a határérték megoldásához egyszerűen ki kell cserélnie azt az értéket, amellyel a funkcióba törekszik x ... Ez azonban a legegyszerűbb eset. A határ megállapítása gyakran nem olyan nyilvánvaló. Olyan bizonytalanságok, mint a 0/0 vagy végtelenség / végtelenség ... Mi a teendő ilyen esetekben? Használjon trükköket!

A bizonytalanság

A végtelenség / végtelenség alakjának bizonytalansága

Legyen egy határ:

Ha megpróbáljuk a végtelenséget helyettesíteni a függvénnyel, akkor a végtelenséget mind a számlálóban, mind a nevezőben kapjuk. Általánosságban el kell mondani, hogy van egy bizonyos művészeti elem az ilyen bizonytalanságok megoldásában: meg kell jegyezni, hogyan lehet egy funkciót úgy átalakítani, hogy a bizonytalanság eltűnjön. Esetünkben a számlálót és a nevezőt osztjuk el x felső fokozatban. Mi történik?

A fentebb már megtekintett példából tudjuk, hogy az a nevezőben x-t tartalmazó kifejezések nullára válnak. Akkor a megoldás a határértékre:

A bizonytalanságok nyilvánosságra hozatala, mint végtelenség / végtelenség ossza meg a számlálót és a nevezőt: x a legmagasabb fokon.

Mellesleg! Olvasóink számára most 10% kedvezmény a

Egy másik típusú bizonytalanság: 0/0

Mint mindig, az értékfüggvény helyettesítése x \u003d -1 ad 0 a számlálóban és a nevezőben. Nézzen egy kicsit közelebbről, és észreveszi, hogy a számlálóban másodlagos egyenlet van. Keresse meg a gyökereket és írja be:

Rövidítsük le és kapjuk meg:

Tehát, ha olyan bizonytalansággal kell szembenéznie, mint például 0/0 - vegye ki a számlálót és a nevezőt.

A példák megoldásának megkönnyítése érdekében táblázatot adunk néhány funkció korlátozásával:

L'Hôpital szabálya belül

Egy másik hatékony módszer mindkét típusú bizonytalanság kiküszöbölésére. Mi a módszer lényege?

Ha bizonytalan a határ, akkor a számláló és a nevező deriváltját vesszük, amíg a bizonytalanság el nem tűnik.

Lopital szabálya így néz ki:

Fontos pont : annak a határnak kell lennie, amelyben a számláló és az nevező helyett a számláló és a nevező származékai vannak.

És most egy valódi példára:

Tipikus bizonytalanság 0/0 ... Vegyük a számláló és a nevező származékait:

Voila, a kétértelműséget gyorsan és elegánsan oldják meg.

Reméljük, hogy hasznos módon tudja felhasználni ezt az információt a gyakorlatban, és megtalálni a választ arra a kérdésre, hogy „hogyan lehet megoldani a korlátokat a felső matematikában”. Ha egy adott szakaszban ki kell számítania egy sorozat vagy a funkció korlátját, és a “egyáltalán” szóból nincs idő erre a munkára, forduljon egy professzionális hallgató szolgálathoz a gyors és részletes megoldás érdekében.