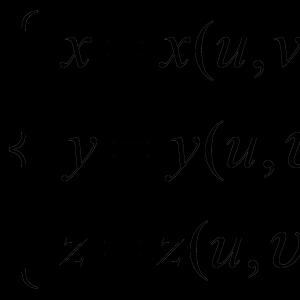L'équation d'une droite en segments a la forme. Équation d'une ligne droite en segments - description, exemples, résolution de problèmes
Nous continuons à étudier la section «L'équation d'une ligne droite sur un plan» et dans cet article, nous analyserons le sujet «L'équation d'une ligne droite en segments». Nous considérerons successivement la forme de l'équation d'une droite en segments, la construction d'une droite, qui est donnée par cette équation, le passage de l'équation générale d'une droite à l'équation d'une droite en segments. Tout cela sera accompagné d'exemples et d'analyses de résolution de problèmes.
Soit un système de coordonnées rectangulaires O x y situé sur le plan.
Une droite sur un plan dans le système de coordonnées cartésien O xy est donnée par une équation de la forme xa + yb = 1 , où a et b sont des nombres réels non nuls dont les valeurs sont égales aux longueurs des segments coupé par une droite sur les axes O x et O y . Les longueurs des segments sont considérées à partir de l'origine des coordonnées.
Comme on le sait, les coordonnées de n'importe lequel des points appartenant à une droite donnée par l'équation d'une droite satisfont l'équation de cette droite. Les points a , 0 et 0 , b appartiennent à cette droite, puisque a a + 0 b = 1 ⇔ 1 ≡ 1 et 0 a + b b = 1 ⇔ 1 ≡ 1 . Les points a , 0 et b , 0 sont situés sur les axes de coordonnées O x et O y et sont éloignés de l'origine par les unités a et b. La direction dans laquelle vous souhaitez reporter la longueur du segment est déterminée par le signe qui précède les nombres a et b. Le signe "-" signifie que la longueur du segment doit être tracée dans le sens négatif de l'axe des coordonnées.
Expliquons tout ce qui précède en plaçant les lignes par rapport à un système de coordonnées cartésien fixe O x y dans un dessin schématique. L'équation d'une droite dans les segments x a + y b = 1 est utilisée pour construire une droite dans le repère cartésien O x y . Pour ce faire, nous devons marquer les points a, 0 et b, 0 sur les axes, puis relier ces points par une ligne à l'aide d'une règle.
Le dessin montre des cas où les nombres a et b ont des signes différents et, par conséquent, les longueurs des segments sont tracées dans différentes directions des axes de coordonnées.
Prenons un exemple.
Exemple 1
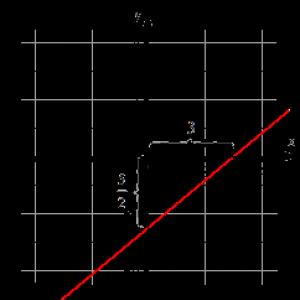
La droite est donnée par l'équation de la droite en segments de la forme x 3 + y - 5 2 = 1 . Il faut construire cette droite sur le plan dans le repère cartésien O x y .
Solution
En utilisant l'équation d'une droite en segments, nous déterminons les points par lesquels passe la droite. C'est 3 0 0 - 5 2 . Marquons-les et traçons une ligne.
Réduction de l'équation générale d'une droite à l'équation d'une droite en segments
Le passage de l'équation donnée d'une ligne droite à l'équation d'une ligne droite en segments nous facilite la résolution de divers problèmes. Ayant l'équation générale complète d'une droite, on peut obtenir l'équation d'une droite en segments.
L'équation générale complète d'une droite dans le plan a la forme A x + B y + C = 0, où A, B et C ne sont pas égaux à zéro. Nous transférons le nombre C sur le côté droit de l'égalité, divisons les deux parties de l'égalité résultante par - C. En même temps, nous envoyons les coefficients pour x et y aux dénominateurs :
UNE X + B y + C = 0 ⇔ UNE X + B y = - C ⇔ ⇔ UNE - C X + B - C y = 1 ⇔ X - C UNE + y - C B = 1
Pour implémenter la dernière transition, nous avons utilisé l'égalité p q = 1 q p , p ≠ 0 , q ≠ 0 .
En conséquence, nous avons fait la transition de l'équation générale de la droite A x + B y + C = 0 à l'équation de la droite dans les segments xa + yb = 1 , où a = - CA , b = -CB.
Considérons l'exemple suivant.
Exemple 2
Faisons la transition vers l'équation d'une droite en segments, ayant l'équation générale d'une droite x - 7 y + 1 2 = 0 .
Solution
On reporte une seconde à droite de l'égalité x - 7 y + 1 2 = 0 ⇔ x - 7 y = - 1 2 .
Divisez les deux membres de l'équation par - 1 2 : x - 7 y = - 1 2 ⇔ 1 - 1 2 x - 7 - 1 2 y = 1 .
Transformons l'égalité résultante à la forme désirée : 1 - 1 2 x - 7 - 1 2 y = 1 ⇔ x - 1 2 + y 1 14 = 1 .
Nous avons obtenu l'équation d'une droite en segments.
Réponse: x - 1 2 + y 1 14 = 1
Dans les cas où une droite est donnée par une équation canonique ou paramétrique d'une droite sur un plan, alors on passe d'abord à l'équation générale d'une droite, puis à l'équation d'une droite en segments.
Passer de l'équation d'une ligne droite en segments et de l'équation générale d'une ligne droite est simple: nous transférons l'unité du côté droit de l'équation d'une ligne droite en segments de la forme xa + yb \u003d 1 vers la gauche côté de signe opposé, on sélectionne les coefficients devant les inconnues x et y.
X une + y b = 1 ⇔ X une + y b - 1 = 0 ⇔ 1 une X + 1 b y - 1 = 0
On obtient l'équation générale d'une droite, à partir de laquelle on peut passer à toute autre forme de l'équation d'une droite dans un plan. Nous avons analysé en détail le processus de transition dans le sujet "Réduction de l'équation générale d'une droite à d'autres types d'équation de droite".
Exemple 3
L'équation d'une droite en segments a la forme x 2 3 + y - 12 = 1. Il faut écrire l'équation générale d'une droite dans un plan.
Solution
Il fonctionne selon un algorithme précédemment décrit :
x 2 3 + y - 12 = 1 ⇔ 1 2 3 x + 1 - 12 y - 1 = 0 ⇔ ⇔ 3 2 x - 1 12 y - 1 = 0
Réponse : 3 2 x - 1 12 y - 1 = 0
Si vous remarquez une erreur dans le texte, veuillez le mettre en surbrillance et appuyer sur Ctrl+Entrée
Équation de ligne droite , où une et b certains nombres réels autres que zéro sont appelés équation d'une droite en segments. Ce nom n'est pas accidentel, puisque les valeurs absolues des nombres une et bégales aux longueurs des segments que la droite coupe sur les axes de coordonnées Bœuf et Oy respectivement (les segments sont comptés à partir de l'origine). Ainsi, l'équation d'une droite en segments permet de construire facilement cette droite dans un dessin. Pour ce faire, marquez des points avec des coordonnées et dans un système de coordonnées rectangulaire sur le plan, et utilisez une règle pour les relier par une ligne droite.
Par exemple, construisons une droite donnée par une équation en segments de la forme . Marquez les points et reliez-les.
Vous pouvez obtenir des informations détaillées sur ce type d'équation d'une droite sur un plan dans l'article équation d'une droite en segments.
Haut de page
Fin du travail -
Ce sujet appartient à :
Algèbre et géométrie analytique. Le concept de matrice, les opérations sur les matrices et leurs propriétés
Le concept d'opérations matricielles sur les matrices et leurs propriétés .. une matrice est un tableau rectangulaire composé de nombres qui ne peuvent pas être .. et l'addition matricielle est une opération par élément ..
Si vous avez besoin de matériel supplémentaire sur ce sujet, ou si vous n'avez pas trouvé ce que vous cherchiez, nous vous recommandons d'utiliser la recherche dans notre base de données d'œuvres :
Que ferons-nous du matériel reçu :
Si ce matériel s'est avéré utile pour vous, vous pouvez l'enregistrer sur votre page sur les réseaux sociaux :
| tweeter |
Tous les sujets de cette section :
Définition de dérivabilité
L'opération de recherche de la dérivée est appelée différenciation d'une fonction. Une fonction est dite dérivable en un point si elle a une dérivée finie en ce point, et
Règle de différenciation
Corollaire 1. Le facteur constant peut être déduit du signe de la dérivée :
La signification géométrique de la dérivée. Équation tangente
L'angle d'inclinaison de la droite y \u003d kx + b est l'angle mesuré à partir de la position
La signification géométrique de la dérivée d'une fonction en un point
Considérons la sécante AB du graphe de la fonction y = f(x) telle que les points A et B aient respectivement des coordonnées
Solution
La fonction est définie pour tous les nombres réels. Puisque (-1; -3) est le point de contact, alors
Conditions nécessaires pour un extremum et conditions suffisantes pour un extremum
Définition d'une fonction croissante. La fonction y = f(x) croît sur l'intervalle X si pour tout
Critères suffisants pour l'extremum d'une fonction
Pour trouver les maxima et les minima de la fonction, vous pouvez utiliser l'un des trois signes suffisants d'un extremum. Bien que le plus courant et le plus pratique soit le premier d'entre eux.
Propriétés de base d'une intégrale définie. Propriété 1. La dérivée d'une intégrale définie par rapport à la limite supérieure est égale à l'intégrale dans laquelle, au lieu d'une variable, est intégrée
Formule de Newton-Leibniz (avec preuve)
Formule de Newton-Leibniz. Soient la fonction y = f(x) continue sur un segment et F(x) une des primitives de la fonction sur ce segment, alors
Soit un système de coordonnées affines OXY donné.
Théorème 2.1. N'importe quelle droite je le système de coordonnées OX est donné par une équation linéaire de la forme
UNE X+B y+ C = O, (1)
où A, B, C R et A 2 + B 2 0. Inversement, toute équation de la forme (1) définit une droite.
Équation de la forme (1) - équation générale d'une droite .
Soit dans l'équation (1) tous les coefficients A, B et C non nuls. Puis
Ah-By=-C, et .
Notons -C/A=a, -C/B=b. Avoir
-équation de segment de droite .
En effet, les nombres |a| et |b| indiquer la taille des segments coupés par une ligne droite je respectivement sur les axes OX et OY.
Laisse la ligne je est donnée par l'équation générale (1) dans un système de coordonnées rectangulaires et laisse les points M 1 (x 1, y 1) et M 2 (x 2, y 2) appartenir je. Puis
UNE X 1 + B à 1 + C = UNE X 2 + B à 2 + C, c'est-à-dire A( X 1 -X 2) + B( à 1 -à 2) = 0.
La dernière égalité signifie que le vecteur \u003d (A, B) est orthogonal au vecteur \u003d (x 1 -x 2, y 1 -y 2). celles. Le vecteur (A, B) est appelé vecteur normal de la droite l.
Considérons le vecteur = (-B, A). Puis
A(-B)+BA=0. celles. ^ .
Par conséquent, le vecteur \u003d (-B, A) est le vecteur de direction de l'épicé je.
Équations paramétriques et canoniques d'une droite
Équation d'une droite passant par deux points donnés
Soit la droite donnée dans le repère affine (0, X, Y) je, son vecteur directeur = (m,n) et le point M 0 ( X 0 ,y 0) possédé je. Alors pour un point quelconque M ( X,à) de cette ligne nous avons
et depuis lors 
.
Si nous désignons et
Les rayons vecteurs des points M et M 0 , respectivement, alors
- équation d'une droite sous forme vectorielle.
Parce que =( X,à), =(X 0 ,à 0), alors
X= X 0 + mt,
y= y 0 + NT
- équation paramétrique d'une droite .
D'où il suit que
- équation canonique d'une droite .
Enfin, si en ligne droite je deux points M 1 ( X 1 ,à 1) et
M2( X 2 ,à 2), alors le vecteur =( X 2 -X 1 ,y 2 -à 1) est guidage vecteur ligne droite je. Puis
- équation d'une droite passant par deux points donnés.
Disposition mutuelle de deux lignes droites.
Laissez tout droit je 1 et je 2 sont donnés par leurs équations générales
je 1 : Un 1 X+ En 1 à+ С 1 = 0, (1)
je 2 : A 2 X+ B 2 à+ C2 = 0.
Théorème. Laissez tout droit je 1 et je 2 sont donnés par les équations (1). Alors et seulement alors :
1) les droites se coupent lorsqu'il n'y a pas de nombre λ tel que
A 1 =λA 2 , B 1 =λB 2 ;
2) les droites coïncident lorsqu'il existe un nombre λ tel que
A 1 =λA 2 , B 1 =λB 2 , C 1 =λC 2 ;
3) les droites sont distinctes et parallèles lorsqu'il existe un nombre λ tel que
A 1 \u003d λA 2, B 1 \u003d λB 2, C 1 λC 2.
faisceau de lignes droites
Un tas de lignes droites est l'ensemble de toutes les droites du plan passant par un point appelé centre rayonner.
Pour spécifier l'équation de la poutre, il suffit de connaître deux droites quelconques je 1 et je 2 passant par le centre du faisceau.
Laissez les lignes dans le système de coordonnées affines je 1 et je 2 sont donnés par les équations
je 1:A1 X+B1 y+ C1 = 0,
je 2:A2 X+ B2 y+ C2 = 0.
L'équation:
Un 1 X+B1 y+ С + λ (A 2 X+ B 2 y+ C) = 0
- l'équation d'un faisceau de droites défini par les équations l 1 et l 2.
Dans ce qui suit, par repère on entend le repère rectangulaire .
Conditions de parallélisme et de perpendicularité de deux droites
Laissez les lignes je 1 et je 2. avec leurs équations générales; = (A 1 ,B 1), = (A 2 ,B 2) sont les vecteurs normaux de ces droites ; k 1 = tanα 1 , k 2 = tgα 2 – coefficients de pente ; =( m 1 ,n 1), (m 2 ,n 2) sont des vecteurs directeurs. Ensuite, directement je 1 et je 2 sont parallèles si et seulement si l'une des conditions suivantes est vraie :
ou soit k 1 =k 2 ou .
Que ce soit droit maintenant je 1 et je 2 sont perpendiculaires. Alors, évidemment, , c'est-à-dire A 1 A 2 + B 1 B 2 = 0.
Si droit je 1 et je 2 sont donnés respectivement par les équations
je 1: à=k 1 X+ b 1 ,
je 2: à=k 2 X+ b 2 ,
alors tgα 2 = tg(90º+α) = 
.
D'où il suit que
Enfin, si et sont les vecteurs directeurs des droites, alors ^ , c'est-à-dire
m 1 m 2 + n 1 n 2 = 0
La dernière relation exprime la condition nécessaire et suffisante pour que deux plans soient perpendiculaires.
Angle entre deux lignes
À un angle φ entre deux lignes je 1 et je 2 nous comprendrons le plus petit angle dont une ligne doit être tournée pour qu'elle devienne parallèle à une autre ligne ou coïncide avec elle, soit 0 £ φ £
Soit les droites données par des équations générales. Il est évident que
cosφ= 
Que ce soit droit maintenant je 1 et je 2 est donné par des équations avec des coefficients de pente k 1 po k 2 respectivement. Puis
Évidemment, c'est ( X-X 0) + B( à-à 0) + C( z-z 0) = 0
Ouvrons les crochets et notons D \u003d -A X 0 - B à 0 - C z 0 . Avoir
UNE X+B y+C z+ D = 0 (*)
- équation générale du plan ou équation générale du plan.
Théorème 3.1 L'équation linéaire (*) (A 2 +B 2 +C 2 ≠ 0) est l'équation du plan et inversement, toute équation du plan est linéaire.
1) D = 0, alors le plan passe par l'origine.
2) A \u003d 0, alors le plan est parallèle à l'axe OX
3) A \u003d 0, B \u003d 0, alors le plan est parallèle au plan OXY.
Soit tous les coefficients de l'équation non nuls.
- équation d'un plan en segments. Les nombres |a|, |b|, |c| indiquent la taille des segments coupés par le plan sur les axes de coordonnées.
Équation d'une droite en segments
Donnons l'équation générale d'une droite :
L'équation d'une droite en segments, où sont les segments que la droite coupe sur les axes de coordonnées correspondants.
Construire une droite donnée par l'équation générale :
A partir de là, vous pouvez construire l'équation de cette droite en segments :
Arrangement mutuel de lignes droites sur un plan.
Déclaration 1.
Dans l'ordre des droites et donné par les équations :
Coïncidant, nécessaire et suffisant que :
Preuve : et coïncident, leurs vecteurs directeurs et sont colinéaires, soit :
Prenons le point M 0 avec ces droites, alors :
En multipliant la première équation par et en ajoutant à la seconde, grâce à (2) on obtient :
Ainsi, les formules (2), (3) et (4) sont équivalentes. Soit (2) ; alors les équations du système (*) sont équivalentes ; les droites correspondantes coïncident.
Déclaration 2.
Les droites et données par les équations (*) sont parallèles et non confondues si et seulement si :
Preuve:
Qu'ils ne correspondent pas :
Inconsistant, c'est-à-dire selon le théorème de Kronecker-Capelli :
Ceci n'est possible que si :
C'est-à-dire sous la condition (5).
Lorsque la première égalité (5) est vérifiée, - la non-réalisation de la deuxième égalité donne l'incohérence du système (*) les droites sont parallèles et ne coïncident pas.
Remarque 1.
Système de coordonnées polaires.
Nous fixons un point sur le plan et l'appelons un pôle. Le rayon issu du pôle s'appelle l'axe polaire.
Nous choisissons une échelle pour mesurer les longueurs des segments et convenons que la rotation dans le sens antihoraire autour de m sera considérée comme positive. Considérez n'importe quel point sur un plan donné, dénotez-le par sa distance au pôle et appelez-le le rayon polaire. L'angle dont l'axe polaire doit être tourné pour qu'il coïncide avec est désigné par et sera appelé l'angle polaire.
Définition 3.
Les coordonnées polaires d'un point sont son rayon polaire et son angle polaire :
Remarque 2. au pôle. La valeur des points autres qu'un point est déterminée jusqu'à un terme.
Considérons un système de coordonnées rectangulaire cartésien : le pôle coïncide avec l'origine et l'axe polaire coïncide avec le demi-axe positif. Ici. Puis:
Quelle est la relation entre les systèmes de coordonnées rectangulaires cartésiennes et polaires.
Équation de la lemniscate de Bernoulli. Écrivez-le en coordonnées polaires.
Équation normale d'une droite dans un plan. Faisons coïncider l'axe polaire avec, - l'axe passant par l'origine. Laisser:
Soit alors :
Condition (**) pour un point :
Équation d'une droite dans le système de coordonnées polaires.
Ici - la longueur tirée de l'origine à la ligne droite, - l'angle d'inclinaison de la normale à l'axe.
L'équation (7) peut être réécrite :
Équation normale d'une droite dans un plan.
Propriétés d'une droite en géométrie euclidienne.
Il y a une infinité de lignes qui peuvent être tracées à travers n'importe quel point.
Par deux points non coïncidents, il n'y a qu'une seule ligne droite.
Deux lignes non coïncidentes dans le plan se coupent en un seul point ou sont
parallèle (succédant de la précédente).
Dans un espace tridimensionnel, il existe trois options pour la position relative de deux lignes :
- les lignes se croisent ;
- les droites sont parallèles ;
- les lignes droites se croisent.
Droit ligne- courbe algébrique du premier ordre : dans le repère cartésien, une droite
est donnée sur le plan par une équation du premier degré (équation linéaire).
Équation générale d'une droite.
Définition. Toute ligne dans le plan peut être donnée par une équation du premier ordre
Ah + Wu + C = 0,
et constante UN B pas égal à zéro en même temps. Cette équation du premier ordre s'appelle général
équation de droite. En fonction des valeurs des constantes UN B et AVEC Les cas particuliers suivants sont possibles :
. C = 0, A ≠ 0, B ≠ 0- la droite passe par l'origine
. A = 0, B ≠0, C ≠0 ( Par + C = 0)- droite parallèle à l'axe Oh
. B = 0, A ≠ 0, C ≠ 0 ( Ax + C = 0)- droite parallèle à l'axe UO
. B = C = 0, A ≠ 0- la ligne coïncide avec l'axe UO
. UNE = C = 0, B ≠ 0- la ligne coïncide avec l'axe Oh
L'équation d'une droite peut être représentée sous différentes formes en fonction de
conditions initiales.
Équation d'une droite par un point et un vecteur normal.
Définition. Dans un système de coordonnées rectangulaires cartésiennes, un vecteur avec des composantes (A, B)
perpendiculaire à la ligne donnée par l'équation
Ah + Wu + C = 0.
Exemple. Trouver l'équation d'une droite passant par un point A(1, 2) perpendiculaire au vecteur (3, -1).
Solution. Composons en A \u003d 3 et B \u003d -1 l'équation de la droite : 3x - y + C \u003d 0. Pour trouver le coefficient C
on substitue dans l'expression résultante les coordonnées du point donné A. On obtient : 3 - 2 + C = 0, donc
C = -1. Total : l'équation souhaitée : 3x - y - 1 \u003d 0.
Équation d'une droite passant par deux points.
Soit deux points donnés dans l'espace M 1 (x 1 , y 1 , z 1) et M2 (x 2, y 2 , z 2), ensuite équation de droite,
passant par ces points :
Si l'un des dénominateurs est égal à zéro, le numérateur correspondant doit être égal à zéro. Sur le
plan, l'équation d'une droite écrite ci-dessus est simplifiée :
si x 1 ≠ x 2 et x = x 1, si x 1 = x 2 .
Fraction = k appelé facteur de pente droit.
Exemple. Trouver l'équation d'une droite passant par les points A(1, 2) et B(3, 4).
Solution. En appliquant la formule ci-dessus, on obtient :
Équation d'une droite par un point et une pente.
Si l'équation générale d'une droite Ah + Wu + C = 0 apporter au formulaire :
et désigner 
, alors l'équation résultante est appelée
équation d'une droite de pente k.
L'équation d'une droite sur un point et un vecteur directeur.
Par analogie avec le point considérant l'équation d'une droite passant par le vecteur normal, vous pouvez saisir la tâche
une droite passant par un point et un vecteur directeur d'une droite.
Définition. Chaque vecteur non nul (α 1 , α 2), dont les composants satisfont la condition
Aα 1 + Bα 2 = 0 appelé vecteur directeur de la droite.
Ah + Wu + C = 0.
Exemple. Trouver l'équation d'une droite de vecteur directeur (1, -1) et passant par le point A(1, 2).
Solution. On va chercher l'équation de la droite recherchée sous la forme : Ax + Par + C = 0. Selon la définition,
les coefficients doivent satisfaire aux conditions :
1 * A + (-1) * B = 0, c'est-à-dire A = B
Alors l'équation d'une droite a la forme : Ax + Ay + C = 0, ou x + y + C / A = 0.
à x=1, y=2 on a C/ A = -3, c'est à dire. équation souhaitée :
x + y - 3 = 0
Équation d'une droite en segments.
Si dans l'équation générale de la droite Ah + Wu + C = 0 C≠0, alors, en divisant par -C, on obtient :
ou où
La signification géométrique des coefficients est que le coefficient a est la coordonnée du point d'intersection
droit avec axe Oh, une b- la coordonnée du point d'intersection de la droite avec l'axe UO.
Exemple. L'équation générale d'une droite est donnée x - y + 1 = 0. Trouver l'équation de cette droite en segments.
C \u003d 1, , un \u003d -1, b \u003d 1.
Équation normale d'une droite.
Si les deux côtés de l'équation Ah + Wu + C = 0 diviser par nombre 
, qui est appelée
facteur de normalisation, alors on obtient
xcosφ + ysinφ - p = 0 -équation normale d'une droite.
Le signe ± du facteur de normalisation doit être choisi de telle sorte que µ * C< 0.
R- la longueur de la perpendiculaire descendue de l'origine à la droite,
une φ - l'angle formé par cette perpendiculaire avec la direction positive de l'axe Oh.
Exemple. Etant donné l'équation générale d'une droite 12x - 5a - 65 = 0. Nécessaire pour écrire divers types d'équations
cette ligne droite.
L'équation de cette droite en segments:
L'équation de cette droite avec la pente: (diviser par 5)
Équation d'une droite:
cosφ = 12/13 ; sin φ= -5/13 ; p=5.
Il convient de noter que toutes les lignes droites ne peuvent pas être représentées par une équation en segments, par exemple des lignes droites,
parallèles aux axes ou passant par l'origine.
Angle entre les droites d'un plan.
Définition. Si deux lignes sont données y \u003d k 1 X + b 1, y \u003d k 2 X + b 2, alors l'angle aigu entre ces lignes
sera défini comme
Deux droites sont parallèles si k 1 = k 2. Deux droites sont perpendiculaires
si k 1 \u003d -1 / k 2 .
Théorème.
Direct Ah + Wu + C = 0 et UNE 1 x + B 1 y + C 1 \u003d 0 sont parallèles lorsque les coefficients sont proportionnels
A 1 \u003d λA, B 1 \u003d λB. Si aussi С 1 \u003d λС, alors les lignes coïncident. Coordonnées du point d'intersection de deux droites
se trouvent comme solution du système d'équations de ces droites.
L'équation d'une droite passant par un point donné est perpendiculaire à une droite donnée.
Définition. Une droite passant par un point M 1 (x 1, y 1) et perpendiculaire à la ligne y = kx + b
représenté par l'équation :
La distance d'un point à une ligne.
Théorème. Si un point est donné M(x 0, y 0), puis la distance à la ligne Ah + Wu + C = 0 défini comme:
Preuve. Laissez le point M 1 (x 1, y 1)- la base de la perpendiculaire descendue du point M pour un donné
direct. Alors la distance entre les points M et M 1:
(1)
Coordonnées x1 et 1 peut être trouvée comme solution du système d'équations :
La deuxième équation du système est l'équation d'une droite passant par un point donné M 0 perpendiculairement
ligne donnée. Si nous transformons la première équation du système sous la forme :
A(x - x 0) + B(y - y 0) + Ax 0 + Par 0 + C = 0,
puis, en résolvant, on obtient :
En remplaçant ces expressions dans l'équation (1), on trouve :
Le théorème a été prouvé.
