Coin côté 2 3 hauteur de base. Hauteur du triangle

Lors de la résolution de problèmes géométriques, il est utile de suivre cet algorithme. Lors de la lecture de l'énoncé de tâche, il est nécessaire

Faites un dessin. Le dessin doit correspondre autant que possible à l'état du problème, sa tâche principale est donc d'aider à trouver la solution
Appliquer toutes les données de la condition de tâche au dessin
Écrivez tous les concepts géométriques qui se produisent dans le problème
Rappelons tous les théorèmes qui se rapportent à ce concept
Mettre sur le dessin toutes les relations entre les éléments d'une figure géométrique qui découlent de ces théorèmes

Par exemple, si la tâche contient les mots bissectrice de l'angle d'un triangle, vous devez vous souvenir de la définition et des propriétés de la bissectrice et désigner des segments et des angles égaux ou proportionnels dans le dessin.

Dans cet article, vous trouverez les propriétés de base d'un triangle que vous devez connaître pour réussir à résoudre des problèmes.

TRIANGLE.

Aire d'un triangle.

1. ,

ici - un côté arbitraire du triangle, - la hauteur abaissée de ce côté.

2. ,

ici et sont des côtés arbitraires du triangle, est l'angle entre ces côtés :

3. Formule Héron :

Ici - les longueurs des côtés du triangle, - le demi-périmètre du triangle,

4. ,

ici - le demi-périmètre du triangle, - le rayon du cercle inscrit.

Soient les longueurs des segments tangents.

La formule de Heron peut alors s'écrire sous la forme suivante :

6. ,

ici - les longueurs des côtés du triangle, - le rayon du cercle circonscrit.

Si un point est pris sur un côté d'un triangle qui divise ce côté dans le rapport m:n, alors le segment reliant ce point au sommet de l'angle opposé divise le triangle en deux triangles dont les aires sont liées par m :n:

Le rapport des aires des triangles semblables est égal au carré du coefficient de similarité.

Médiane triangulaire

Il s'agit d'un segment de droite qui relie le sommet du triangle au milieu du côté opposé.

Médianes des triangles se croisent en un point et partagent le point d'intersection dans un rapport de 2:1, en partant du haut.

Le point d'intersection des médianes d'un triangle régulier divise la médiane en deux segments dont le plus petit est égal au rayon du cercle inscrit et le plus grand est égal au rayon du cercle circonscrit.

Le rayon du cercle circonscrit est le double du rayon du cercle inscrit : R=2r

Longueur médiane triangle arbitraire

ici - la médiane dessinée sur le côté - les longueurs des côtés du triangle.

Bissectrice d'un triangle

C'est un segment de la bissectrice de n'importe quel angle d'un triangle, reliant le sommet de cet angle au côté opposé.

Bissectrice d'un triangle divise le côté en segments proportionnels aux côtés adjacents :

Bissectrices du triangle se coupent en un point, qui est le centre du cercle inscrit.

Tous les points de la bissectrice d'un angle sont équidistants des côtés de l'angle.

Hauteur du triangle

C'est un segment de la perpendiculaire, abaissé du sommet du triangle à le côté opposé, ou sa suite. Dans un triangle obtus, l'altitude tirée du sommet d'un angle aigu se trouve à l'extérieur du triangle.

Les hauteurs d'un triangle se coupent en un point appelé l'orthocentre du triangle.

Pour trouver la hauteur d'un triangle dessiné sur le côté, vous devez trouver son aire de toutes les manières possibles, puis utiliser la formule :

Centre d'un cercle circonscrit à un triangle, se situe au point d'intersection des bissectrices perpendiculaires tracées sur les côtés du triangle.

Le rayon du cercle circonscrit d'un triangle peut être trouvé à l'aide des formules suivantes :

Voici les longueurs des côtés du triangle, aire d'un triangle.

où est la longueur du côté du triangle, est l'angle opposé. (Cette formule découle du théorème des sinus).

inégalité triangulaire

Chaque côté du triangle est inférieur à la somme et supérieur à la différence des deux autres.

La somme des longueurs de deux côtés est toujours supérieure à la longueur du troisième côté :

En face du grand côté se trouve un angle plus grand ; en face de l'angle le plus grand se trouve le côté le plus grand :

Si , alors vice versa.

Théorème des sinus :

Les côtés d'un triangle sont proportionnels aux sinus des angles opposés :

Théorème du cosinus :

le carré d'un côté d'un triangle est égal à la somme des carrés des deux autres côtés sans doubler le produit de ces côtés par le cosinus de l'angle entre eux :

Triangle rectangle

- C'est un triangle dont l'un des angles est égal à 90°.

Somme coins pointus triangle rectangle est égal à 90°.

L'hypoténuse est le côté opposé à l'angle de 90°. L'hypoténuse est le côté le plus long.

Théorème de Pythagore:

le carré de l'hypoténuse est égal à la somme des carrés des jambes:

Le rayon d'un cercle inscrit dans un triangle rectangle est

ici - le rayon du cercle inscrit, - les jambes, - l'hypoténuse :

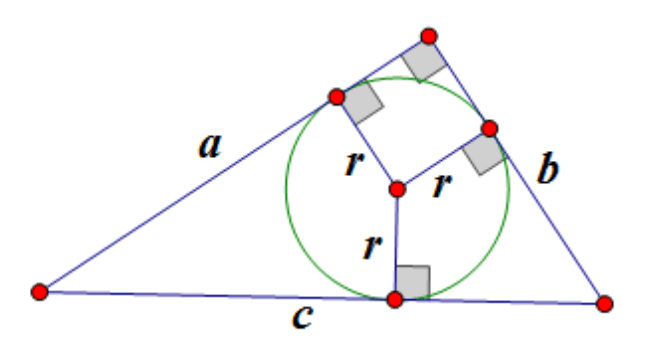
Centre d'un cercle circonscrit à un triangle rectangle se situe au milieu de l'hypoténuse :

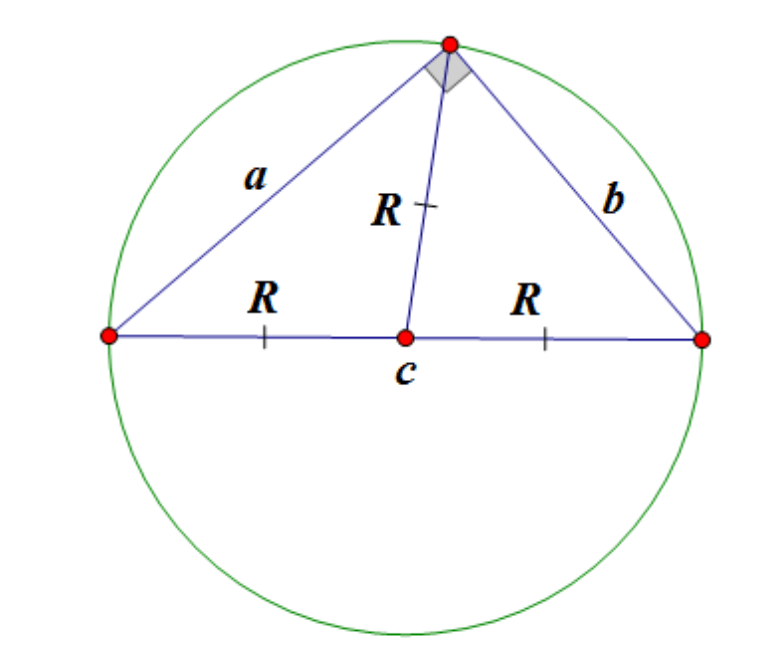
Médiane d'un triangle rectangle tiré vers l'hypoténuseégale à la moitié de l'hypoténuse.

Définition du sinus, du cosinus, de la tangente et de la cotangente d'un triangle rectangle voir

Le rapport des éléments dans un triangle rectangle :

Le carré de la hauteur d'un triangle rectangle tiré d'un sommet angle droit, est égal au produit des projections des jambes sur l'hypoténuse :

Le carré de la jambe est égal au produit de l'hypoténuse et de la projection de la jambe sur l'hypoténuse :

Jambe couchée contre le coin égale à la moitié de l'hypoténuse :

Triangle isocèle.

Bissecteur triangle isocèle tiré à la base est la médiane et la hauteur.

Dans un triangle isocèle, les angles à la base sont égaux.

Angle supérieur.

Je - côtés

Et - angles à la base.

Hauteur, bissectrice et médiane.

Attention! La hauteur, la bissectrice et la médiane dessinées sur le côté latéral ne correspondent pas.

triangle rectangle

(ou triangle équilatéral ) est un triangle dont tous les côtés et angles sont égaux.

Aire d'un triangle équilatéral est égal à

où est la longueur du côté du triangle.

Centre d'un cercle inscrit dans un triangle équilatéral, coïncide avec le centre du cercle circonscrit à un triangle équilatéral et se situe au point d'intersection des médianes.

Point d'intersection des médianes d'un triangle équilatéral divise la médiane en deux segments dont le plus petit est égal au rayon du cercle inscrit et le plus grand est égal au rayon du cercle circonscrit.

Si l'un des angles d'un triangle isocèle mesure 60°, alors le triangle est régulier.

Ligne médiane du triangle

C'est un segment qui relie les milieux de deux côtés.

Dans la figure, DE est la ligne médiane du triangle ABC.

La ligne médiane du triangle est parallèle au troisième côté et égale à la moitié de celui-ci : DE||AC, AC=2DE

Angle externe d'un triangle

C'est l'angle adjacent à n'importe quel angle du triangle.

Un angle extérieur d'un triangle est égal à la somme de deux angles qui ne lui sont pas adjacents.

Fonctions trigonométriques d'un angle externe :

Signes d'égalité des triangles :

1 . Si deux côtés et l'angle entre eux d'un triangle sont respectivement égaux à deux côtés et l'angle entre eux d'un autre triangle, alors ces triangles sont congruents.

2 . Si un côté et deux angles adjacents d'un triangle sont respectivement égaux à un côté et deux angles adjacents d'un autre triangle, alors ces triangles sont congruents.

3 Si trois côtés d'un triangle sont respectivement égaux à trois côtés d'un autre triangle, alors ces triangles sont congruents.

Important: puisque dans un triangle rectangle deux angles sont évidemment égaux, alors pour égalité de deux triangles rectangles seuls deux éléments doivent être égaux : deux côtés, ou un côté et un angle aigu.

Signes de similitude des triangles :

1 . Si deux côtés d'un triangle sont proportionnels à deux côtés d'un autre triangle et que les angles compris entre ces côtés sont égaux, alors ces triangles sont semblables.

2 . Si trois côtés d'un triangle sont proportionnels à trois côtés d'un autre triangle, alors ces triangles sont semblables.

3 . Si deux angles d'un triangle sont égaux à deux angles d'un autre triangle, alors ces triangles sont semblables.

Important: Dans les triangles semblables, les côtés semblables sont opposés à des angles égaux.

Théorème de Ménélas

Soit la droite coupe le triangle , où est le point de son intersection avec le côté , est le point de son intersection avec le côté , et est le point de son intersection avec le prolongement du côté . Alors

Votre vie privée est importante pour nous. Pour cette raison, nous avons développé une politique de confidentialité qui décrit comment nous utilisons et stockons vos informations. Veuillez lire notre politique de confidentialité et faites-nous savoir si vous avez des questions.

Collecte et utilisation des informations personnelles

Les informations personnelles font référence aux données qui peuvent être utilisées pour identifier ou contacter une personne spécifique.

Vous pouvez être invité à fournir vos informations personnelles à tout moment lorsque vous nous contactez.

Voici quelques exemples des types d'informations personnelles que nous pouvons collecter et de la manière dont nous pouvons utiliser ces informations.

Quelles informations personnelles nous collectons :

Lorsque vous soumettez une candidature sur le site, nous pouvons collecter diverses informations, notamment votre nom, votre numéro de téléphone, votre adresse e-mail, etc.

Comment utilisons-nous vos informations personnelles:

Collecté par nos soins informations personnelles nous permet de vous contacter et de vous informer des offres uniques, promotions et autres événements et événements à venir.
De temps à autre, nous pouvons utiliser vos informations personnelles pour vous envoyer des avis et des communications importants.
Nous pouvons également utiliser des informations personnelles à des fins internes, telles que la réalisation d'audits, l'analyse de données et diverses recherches afin d'améliorer les services que nous fournissons et de vous fournir des recommandations concernant nos services.
Si vous participez à un tirage au sort, à un concours ou à une incitation similaire, nous pouvons utiliser les informations que vous fournissez pour administrer ces programmes.

Divulgation à des tiers

Nous ne divulguons pas les informations reçues de votre part à des tiers.

Des exceptions:

Si nécessaire - conformément à la loi, à une ordonnance judiciaire, dans le cadre d'une procédure judiciaire et / ou sur la base de demandes publiques ou de demandes de organismes gouvernementaux sur le territoire de la Fédération de Russie - divulguez vos informations personnelles. Nous pouvons également divulguer des informations vous concernant si nous déterminons qu'une telle divulgation est nécessaire ou appropriée à des fins de sécurité, d'application de la loi ou à d'autres fins d'intérêt public.
En cas de réorganisation, de fusion ou de vente, nous pouvons transférer les informations personnelles que nous collectons au tiers successeur concerné.

Protection des informations personnelles

Nous prenons des précautions - y compris administratives, techniques et physiques - pour protéger vos informations personnelles contre la perte, le vol et l'utilisation abusive, ainsi que contre l'accès, la divulgation, l'altération et la destruction non autorisés.

Maintenir votre vie privée au niveau de l'entreprise

Pour garantir la sécurité de vos informations personnelles, nous communiquons les pratiques de confidentialité et de sécurité à nos employés et appliquons strictement les pratiques de confidentialité.

E UNE → ⋅ B C → + E B → ⋅ C UNE → + E C → ⋅ UNE B → = 0 (\displaystyle (\overrightarrow (EA))\cdot (\overrightarrow (BC))+(\overrightarrow (EB))\cdot (\ overrightarrow (CA))+(\overrightarrow (EC))\cdot (\overrightarrow (AB))=0)

(Pour prouver l'identité, il faut utiliser les formules

UNE B → = E B → − E UNE → , B C → = E C → − E B → , C UNE → = E UNE → − E C → (\displaystyle (\overrightarrow (AB))=(\overrightarrow (EB))-(\overrightarrow (EA )),\,(\overrightarrow (BC))=(\overrightarrow (EC))-(\overrightarrow (EB)),\,(\overrightarrow (CA))=(\overrightarrow (EA))-(\overrightarrow (CE)))

Le point E doit être pris comme l'intersection des deux hauteurs du triangle.)

Orthocentre isogonalement conjugué au centre cercle circonscrit .
Orthocentre se trouve sur la même ligne que le barycentre, le centre cercle circonscrit et le centre du cercle de neuf points (voir la droite d'Euler).
Orthocentre un triangle aigu est le centre d'un cercle inscrit dans son orthotriangle.
Le centre d'un triangle décrit par l'orthocentre avec des sommets au milieu des côtés du triangle donné. Le dernier triangle est appelé triangle supplémentaire par rapport au premier triangle.
La dernière propriété peut être formulée comme suit : Le centre d'un cercle circonscrit à un triangle sert orthocentre triangle supplémentaire.
Pointes, symétriques orthocentre triangle par rapport à ses côtés reposent sur le cercle circonscrit.
Pointes, symétriques orthocentre les triangles par rapport aux milieux des côtés reposent également sur le cercle circonscrit et coïncident avec des points diamétralement opposés aux sommets correspondants.
Si À PROPOS est le centre du cercle circonscrit ΔABC, alors O H → = O UNE → + O B → + O C → (\displaystyle (\overrightarrow (OH))=(\overrightarrow (OA))+(\overrightarrow (OB))+(\overrightarrow (OC))) ,
La distance entre le sommet du triangle et l'orthocentre est le double de la distance entre le centre du cercle circonscrit et le côté opposé.
Tout segment tiré de orthocentre coupe toujours le cercle d'Euler jusqu'à ce qu'il coupe le cercle circonscrit. Orthocentre est le centre de l'homothétie de ces deux cercles.
Théorème de Hamilton. Trois segments de ligne reliant l'orthocentre aux sommets d'un triangle à angle aigu le divisent en trois triangles ayant le même cercle d'Euler (cercle de neuf points) que le triangle à angle aigu d'origine.
Conséquences du théorème de Hamilton:
- Trois segments de droite reliant l'orthocentre aux sommets d'un triangle à angle aigu le divisent en trois Triangle d'Hamilton ayant des rayons égaux de cercles circonscrits.
- Les rayons des cercles circonscrits des trois Triangles d'Hamilton sont égaux au rayon du cercle circonscrit au triangle aigu d'origine.
Dans un triangle aigu, l'orthocentre se trouve à l'intérieur du triangle ; en obtus - à l'extérieur du triangle; dans un rectangle - au sommet d'un angle droit.

Propriétés d'élévation d'un triangle isocèle

Si dans un triangle deux hauteurs sont égales, alors le triangle est isocèle (théorème de Steiner-Lemus), et la troisième hauteur est à la fois la médiane et la bissectrice de l'angle d'où il émerge.
L'inverse est également vrai : dans un triangle isocèle, deux hauteurs sont égales et la troisième hauteur est à la fois une médiane et une bissectrice.
Un triangle équilatéral a les trois hauteurs égales.

Propriétés des bases des hauteurs d'un triangle

Fondations les hauteurs forment ce qu'on appelle l'orthotriangle, qui a ses propres propriétés.
Le cercle décrit près de l'orthotriangle est le cercle d'Euler. Trois milieux des côtés du triangle et trois milieux des trois segments reliant l'orthocentre aux sommets du triangle se trouvent également sur ce cercle.
Une autre formulation de la dernière propriété :
- Théorème d'Euler pour un cercle de neuf points. Fondations trois hauteurs triangle arbitraire, les milieux de ses trois côtés ( fondements de son intérieur médianes) et les milieux des trois segments reliant ses sommets à l'orthocentre, se trouvent tous sur le même cercle (sur cercle à neuf points).
Théorème. Dans tout triangle, le segment de droite reliant terrains deux hauteurs triangle coupe un triangle semblable à celui donné.
Théorème. Dans un triangle, le segment de droite reliant terrains deux hauteurs triangles sur deux côtés antiparallèle un tiers avec lequel il n'a aucun point commun. Par ses deux extrémités, ainsi que par deux sommets du troisième côté mentionné, il est toujours possible de tracer un cercle.

Autres propriétés des hauteurs de triangle

Propriétés de la hauteur minimale d'un triangle

La hauteur minimale d'un triangle a de nombreuses propriétés extrêmes. Par exemple:

La projection orthogonale minimale d'un triangle sur des lignes situées dans le plan du triangle a une longueur égale à la plus petite de ses hauteurs.
La coupe droite minimale dans le plan de passage d'une plaque triangulaire inflexible doit avoir une longueur égale à la plus petite des hauteurs de cette plaque.
Avec un mouvement continu de deux points le long du périmètre du triangle l'un vers l'autre, la distance maximale entre eux lors du mouvement de la première rencontre à la seconde ne peut être inférieure à la longueur de la plus petite des hauteurs du triangle.
La hauteur minimale dans un triangle est toujours à l'intérieur de ce triangle.

Rapports de base

h une = b péché ⁡ γ = c péché ⁡ β , (\displaystyle h_(a)=b\sin \gamma =c\sin \beta ,)
h une = 2 S une , (\displaystyle h_(a)=(\frac (2S)(a)),) Où S (\displaystyle S)- aire d'un triangle, un (\displaystyle un)- la longueur du côté du triangle sur lequel la hauteur est abaissée.
h une 2 = 1 2 (b 2 + c 2 − 1 2 (a 2 + (b 2 − c 2) 2 une 2)) (\displaystyle h_(a)^(2)=(\frac (1)(2 ))(b^(2)+c^(2)-(\frac (1)(2))(a^(2)+(\frac ((b^(2)-c^(2))^ (2))(a^(2))))))
h une = b c 2 R , (\displaystyle h_(a)=(\frac (bc)(2R)),) Où bc (\displaystyle bc)- le produit des faces, R - (\displaystyle R-) rayon du cercle circonscrit
h une : h b : h c = 1 une : 1 b : 1 c = b c : une c : une b (\displaystyle h_(a):h_(b):h_(c)=(\frac (1)(a)):( \frac (1)(b)):(\frac (1)(c))=bc:ac:ab)
1 h une + 1 h b + 1 h c = 1 r (\displaystyle (\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_ (c)))=(\frac (1)(r))), Où r (\ displaystyle r) est le rayon du cercle inscrit.
S = 1 (1 h une + 1 h b + 1 h c) ⋅ (1 h une + 1 h b − 1 h c) ⋅ (1 h une + 1 h c − 1 h b) ⋅ (1 h b + 1 h c − 1 h une) (\displaystyle S =(\frac (1)(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_(c ))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\frac (1)(h_(c))) )(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1)(h_(b))))(\ cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_(a)))))))), Où S (\displaystyle S)- aire d'un triangle.
une = 2 h une ⋅ (1 h une + 1 h b + 1 h c) ⋅ (1 h une + 1 h b − 1 h c) ⋅ (1 h une + 1 h c − 1 h b) ⋅ (1 h b + 1 h c − 1 h une) (\ style d'affichage a=(\frac (2)(h_(a)(\cdot )(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b))) +(\frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\ frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1 )(h_(b))))(\cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_ (un))))))))), un (\displaystyle un)- le côté du triangle auquel tombe la hauteur h une (\displaystyle h_(a)).
La hauteur d'un triangle isocèle abaissé à la base : h c = 1 2 4 une 2 - c 2 , (\displaystyle h_(c)=(\frac (1)(2))(\sqrt (4a^(2)-c^(2))),)

Où c (\ displaystyle c)- base, un (\displaystyle un) - côté.

Théorème sur la hauteur d'un triangle rectangle

Si la hauteur dans un triangle rectangle A B C (\displaystyle ABC) longueur h (\ displaystyle h), tiré du sommet d'un angle droit, divise l'hypoténuse de longueur c (\ displaystyle c) en segments m (\displaystyle m) Et n (\displaystyle n) correspondant aux jambes b (\ displaystyle b) Et un (\displaystyle un), alors les égalités suivantes sont vraies.

Pour résoudre de nombreux problèmes géométriques, vous devez trouver la hauteur d'une figure donnée. Ces tâches ont valeur appliquée. Lors de travaux de construction, la détermination de la hauteur aide à calculer quantité requise matériaux, ainsi que la précision avec laquelle les pentes et les ouvertures sont réalisées. Souvent, pour créer des modèles, vous devez avoir une idée des propriétés

Beaucoup de gens, malgré de bonnes notes à l'école, lors de la construction ordinaire formes géométriques la question se pose de savoir comment trouver la hauteur d'un triangle ou d'un parallélogramme. Et c'est le plus difficile. En effet, un triangle peut être aigu, obtus, isocèle ou droit. Chacun d'eux a ses propres règles de construction et de calcul.

Comment trouver la hauteur d'un triangle dans lequel tous les angles sont aigus, graphiquement

Si tous les angles du triangle sont aigus (chaque angle du triangle est inférieur à 90 degrés), alors pour trouver la hauteur, procédez comme suit.

Selon les paramètres donnés, nous construisons un triangle.
Introduisons la notation. A, B et C seront les sommets de la figure. Les angles correspondant à chaque sommet sont α, β, γ. Les côtés opposés à ces coins sont a, b, c.
La hauteur est la perpendiculaire du sommet de l'angle au côté opposé du triangle. Pour trouver les hauteurs d'un triangle, on construit des perpendiculaires : du sommet de l'angle α au côté a, du sommet de l'angle β au côté b, etc.
Le point d'intersection de la hauteur et du côté a sera noté H1, et la hauteur elle-même sera h1. Le point d'intersection de la hauteur et du côté b sera H2, la hauteur, respectivement, h2. Pour le côté c, la hauteur sera h3 et le point d'intersection H3.

Hauteur dans un triangle avec un angle obtus

Considérons maintenant comment trouver la hauteur d'un triangle s'il y en a une (supérieure à 90 degrés). Dans ce cas, la hauteur tirée d'un angle obtus sera à l'intérieur du triangle. Les deux hauteurs restantes seront à l'extérieur du triangle.

Soit les angles α et β de notre triangle aigus et l'angle γ obtus. Ensuite, pour construire les hauteurs issues des angles α et β, il faut continuer les côtés du triangle qui leur sont opposés afin de tracer des perpendiculaires.

Comment trouver la hauteur d'un triangle isocèle

Ce chiffre a deux côtés égaux et la base, tandis que les angles à la base sont également égaux entre eux. Cette égalité des côtés et des angles facilite la construction des hauteurs et leur calcul.

D'abord, dessinons le triangle lui-même. Soit les côtés b et c, ainsi que les angles β, γ respectivement égaux.

Dessinons maintenant une hauteur à partir du sommet de l'angle α, notons-la h1. Car cette hauteur sera à la fois la bissectrice et la médiane.

Une seule construction peut être réalisée pour la fondation. Par exemple, dessinez une médiane - un segment reliant le sommet d'un triangle isocèle et le côté opposé, la base, pour trouver la hauteur et la bissectrice. Et pour calculer la longueur de la hauteur des deux autres côtés, vous ne pouvez construire qu'une seule hauteur. Ainsi, pour déterminer graphiquement comment calculer la hauteur d'un triangle isocèle, il suffit de trouver deux hauteurs sur trois.

Comment trouver la hauteur d'un triangle rectangle

Il est beaucoup plus facile de déterminer les hauteurs d'un triangle rectangle que d'autres. C'est parce que les jambes elles-mêmes forment un angle droit, ce qui signifie qu'elles sont en hauteur.

Pour construire la troisième hauteur, comme d'habitude, une perpendiculaire est tracée reliant le sommet de l'angle droit et le côté opposé. Par conséquent, pour créer un triangle dans ce cas, une seule construction est nécessaire.