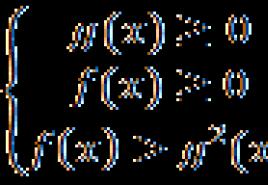Tiešsaistes lineārās nevienlīdzības risinājums ar detalizētu risinājumu. Lineārā nevienlīdzība

Diagramma 5. attēlā:

Un nākamais piemērs: Atrisiniet nevienlīdzību 0,6 2x - 3< 0,36 .

Pēc shēmas 5. attēlā mēs iegūstam
2x - 3> log 0,6 0,36,
2x - 3> 2,
2x> 5,
x> 2,5

Atbilde: (2,5; +∞) .

Apsveriet pēdējo shēmu, kā atrisināt formas nevienlīdzību un f (x)< b , plkst a> 0 un b<0 parādīts 6. attēlā:

Piemēram, atrisināsim nevienlīdzību:

Mēs atzīmējam, ka neatkarīgi no tā, kādu skaitli mēs aizstājam ar x, nevienlīdzības kreisā puse vienmēr ir lielāka par nulli, un mūsu izteiksme ir mazāka par -8, t.i. un nulle, tad risinājumu nav.

Atbilde: risinājumu nav.

Zinot, kā tiek atrisinātas vienkāršākās eksponenciālās nevienlīdzības, var turpināt eksponenciālās nevienlīdzības risināšana.

1. piemērs.

Atrodiet lielāko veselā skaitļa vērtību x, kas atbilst nevienlīdzībai

Tā kā 6 x ir lielāks par nulli (jebkuram x saucējs nepazūd), mēs nevienādības abas puses reizinām ar 6 x, iegūstam:

440 - 2 6 2x> 8, tad
- 2 6 2x> 8 - 440,
- 2 6 2x> - 332,
6 2x< 216,
2x< 3,

x< 1,5. Наибольшее целое число из помежутка (–∞; 1,5) это число 1.

Atbilde: 1.

2. piemērs.

Atrisiniet nevienlīdzību 2 2 x - 3 2 x + 2 ≤ 0

Mēs apzīmējam 2 x caur y, iegūstam nevienlīdzību y 2 - 3y + 2 ≤ 0, mēs atrisinām šo kvadrātveida nevienlīdzību.

y 2 - 3y +2 = 0,
y 1 = 1 un y 2 = 2.

Parabolas zari ir vērsti uz augšu, mēs attēlosim grafiku:

Tad nevienlīdzības risinājums ir nevienlīdzība 1< у < 2, вернемся к нашей переменной х и получим неравенство 1< 2 х < 2, решая которое и найдем ответ 0 < x < 1.

Atbilde: (0; 1) .

3. piemērs... Atrisiniet nevienlīdzību 5 x +1 - 3 x +2< 2·5 x – 2·3 x –1
Apkoposim izteicienus ar vienādiem pamatiem nevienlīdzības vienā daļā

5 x +1 - 2,5 x< 3 x +2 – 2·3 x –1

Mēs izņemam 5 x nevienlīdzības kreisajā pusē un 3 x nevienlīdzības labajā pusē, un mēs iegūstam nevienlīdzību

5 x (5 - 2)< 3 х (9 – 2/3),
3 5 x< (25/3)·3 х

Abas nevienlīdzības puses dalām ar izteiksmi 3 3 x, nevienlīdzības zīme nemainās, jo 3 3 x ir pozitīvs skaitlis, iegūstam nevienlīdzību:

x< 2 (так как 5/3 > 1).

Atbilde: (–∞; 2) .

Ja jums ir kādi jautājumi par eksponenciālu nevienlīdzību risināšanu vai vēlaties praktizēt līdzīgu piemēru risināšanu, reģistrējieties manās nodarbībās. Skolotāja Valentīna Gaļinevskaja.

vietnei, pilnībā vai daļēji nokopējot materiālu, ir nepieciešama saite uz avotu.

Nevienlīdzības risināšana tiešsaistē

Pirms nevienlīdzību risināšanas ir labi jāsaprot, kā tiek atrisināti vienādojumi.

Nav svarīgi, vai nevienlīdzība ir stingra () vai nav stingra (≤, ≥), pirmais solis ir vienādojuma atrisināšana, nevienlīdzības zīmi aizstājot ar vienlīdzību (=).

Paskaidrosim, ko nozīmē novērst nevienlīdzību?

Pēc studenta galvas vienādojumu izpētīšanas izveidojas šāds attēls: jums jāatrod tādas mainīgā vērtības, kurām abas vienādojuma puses ņem vienādas vērtības. Citiem vārdiem sakot, atrodiet visus punktus, kur ir vienlīdzība. Pareizi!

Kad mēs runājam par nevienlīdzību, mēs domājam atrast intervālus (segmentus), kuros pastāv nevienlīdzība. Ja nevienlīdzībā ir divi mainīgie, tad risinājums vairs nebūs intervāli, bet daži apgabali plaknē. Uzminiet, kāds būs trīs mainīgo nevienlīdzības risinājums?

Kā tikt galā ar nevienlīdzību?

Universāla nevienlīdzību risināšanas metode tiek uzskatīta par intervālu metodi (jeb intervālu metodi), kas sastāv no visu intervālu noteikšanas, kuros noteiktā nevienlīdzība tiks apmierināta.

Neiedziļinoties nevienlīdzības tipā, šajā gadījumā tā nav būtība, ir nepieciešams atrisināt atbilstošo vienādojumu un noteikt tā saknes, kam seko šo risinājumu apzīmējums uz skaitļa ass.

Kā pareizi pierakstīt nevienlīdzības risinājumu?

Kad esat noteicis nevienlīdzības risinājumu intervālus, jums pareizi jāizraksta pats risinājums. Ir svarīga nianse - vai intervālā esošās robežas ir iekļautas risinājumā?

Šeit viss ir vienkāršs. Ja vienādojuma risinājums apmierina GDV un nevienlīdzība nav stingra, tad intervāla robeža tiek iekļauta nevienlīdzības risinājumā. Pretējā gadījumā nē.

Ņemot vērā katru intervālu, nevienlīdzības risinājums var būt pats intervāls vai pusintervāls (kad viena no tā robežām apmierina nevienlīdzību), vai segments - intervāls kopā ar tā robežām.

Svarīgs punkts

Nedomājiet, ka tikai intervāli, pus intervāli un līniju segmenti var būt risinājums nevienlīdzībai. Nē, risinājums var ietvert atsevišķus punktus.

Piemēram, nevienādībai | x | ≤0 ir tikai viens risinājums - tas ir punkts 0.

Un nevienlīdzība | x |

Kam domāts nevienlīdzības kalkulators?

Nevienlīdzības kalkulators sniedz pareizo galīgo atbildi. Šajā gadījumā vairumā gadījumu tiek sniegta skaitliskās ass vai plaknes ilustrācija. Var redzēt, vai intervālā esošās robežas ir iekļautas risinājumā vai nav - punkti tiek parādīti kā aizpildīti vai caurdurti.

Pateicoties tiešsaistes nevienlīdzības kalkulatoram, jūs varat pārbaudīt, vai esat pareizi atradis vienādojuma saknes, atzīmējis tos uz skaitļa ass un pārbaudījis nevienlīdzības nosacījumu intervālos (un robežās)?

Ja jūsu atbilde atšķiras no kalkulatora atbildes, jums noteikti vēlreiz jāpārbauda lēmums un jānosaka kļūda.

Nevienlīdzība ir skaitliska attiecība, kas ilustrē skaitļu lielumu attiecībā pret otru. Nevienlīdzības tiek plaši izmantotas, meklējot daudzumus lietišķajās zinātnēs. Mūsu kalkulators palīdzēs jums tikt galā ar tik sarežģītu tēmu kā lineārās nevienlīdzības risināšana.

Kas ir nevienlīdzība

Nevienlīdzīgas attiecības reālajā dzīvē ir saistītas ar pastāvīgu dažādu objektu salīdzināšanu: augstāku vai zemāku, tālāk vai tuvāk, smagāku vai vieglāku. Intuitīvi vai vizuāli mēs varam saprast, ka viens objekts ir lielāks, augstāks vai smagāks par otru, bet patiesībā mēs vienmēr runājam par skaitļu salīdzināšanu, kas raksturo atbilstošās vērtības. Objektus var salīdzināt pēc jebkura kritērija, un jebkurā gadījumā mēs varam sastādīt skaitlisku nevienlīdzību.

Ja nezināmie lielumi īpašos apstākļos ir vienādi, tad to skaitliskai noteikšanai mēs izveidojam vienādojumu. Ja nē, tad "vienādas" zīmes vietā mēs varam norādīt jebkuru citu attiecību starp šīm vērtībām. Divi skaitļi vai matemātiski objekti var būt lielāki par ">", mazāki par "<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.

Nevienlīdzības zīmes to mūsdienu formā izgudroja britu matemātiķis Tomass Garijots, kurš 1631. gadā publicēja grāmatu par nevienlīdzīgām attiecībām. Zīmes, kas lielākas par ">" un mazākas par "<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.

Nevienlīdzību risināšana

Nevienlīdzības, tāpat kā vienādojumi, ir dažāda veida. Lineārās, kvadrātveida, logaritmiskās vai eksponenciālās nevienādās attiecības tiek atdalītas ar dažādām metodēm. Tomēr neatkarīgi no metodes jebkura nevienlīdzība vispirms jāsamazina līdz standarta formai. Tam tiek izmantotas identiskas transformācijas, kas ir vienādas ar vienādību modifikācijām.

Identiskas nevienlīdzības transformācijas

Šādas izteicienu transformācijas ir ļoti līdzīgas vienādojumu spokam, tomēr tām ir nianses, kuras ir svarīgi ņemt vērā, atvienojot nevienlīdzību.

Pirmā identiskā transformācija ir identiska analogajai darbībai ar vienādībām. Abām nevienlīdzīgas attiecības pusēm jūs varat pievienot vai atņemt to pašu skaitli vai izteicienu ar nezināmu x, savukārt nevienlīdzības zīme paliks nemainīga. Visbiežāk šī metode tiek izmantota vienkāršotā formā kā izteiksmes noteikumu pārnešana caur nevienlīdzības zīmi ar skaitļa zīmes izmaiņām pretējā. Tas nozīmē izmaiņas paša termina zīmē, tas ir, + R, pārnesot to caur jebkuru nevienlīdzības pazīmi, mainīsies uz - R un otrādi.

Otrajai transformācijai ir divi punkti:

1. Abas nevienlīdzīgas attiecības puses ir atļauts reizināt vai dalīt ar to pašu pozitīvo skaitli. Šajā gadījumā pati nevienlīdzības pazīme nemainīsies.
2. Abas nevienlīdzības puses ir atļauts sadalīt vai reizināt ar to pašu negatīvo skaitli. Pati nevienlīdzības pazīme tiks mainīta.

Otrajai identiskajai nevienlīdzību transformācijai ir nopietnas atšķirības ar vienādojumu modifikāciju. Pirmkārt, reizinot / dalot ar negatīvu skaitli, nevienlīdzīgas izteiksmes zīme vienmēr tiek apvērsta. Otrkārt, relācijas daļu dalīšana vai reizināšana ir atļauta tikai ar skaitli, nevis ar jebkuru izteiksmi, kas satur nezināmu. Fakts ir tāds, ka mēs nevaram droši zināt, vai aiz nezināmā ir paslēpts skaitlis, kas ir lielāks vai mazāks par nulli, tāpēc otrā identiskā transformācija tiek piemērota nevienādībām tikai ar skaitļiem. Apskatīsim šos noteikumus ar piemēriem.

Nevienlīdzības atraisīšanas piemēri

Algebras uzdevumos ir visdažādākie nevienlīdzības uzdevumi. Ļaujiet mums dot izteicienu:

6x - 3 (4x + 1)> 6.

Vispirms atvērsim iekavas un visus nezināmos pārvietosim pa kreisi un visus skaitļus pa labi.

6x - 12x> 6 + 3

Mums abas izteiksmes puses jāsadala ar −6, ​​tāpēc, atrodot nezināmo x, nevienlīdzības zīme mainīsies pretēji.

Risinot šo nevienlīdzību, mēs izmantojām abas identiskās transformācijas: visus ciparus pārcēlām pa labi no zīmes un abas proporcijas puses dalījām ar negatīvu skaitli.

Mūsu programma ir kalkulators skaitlisko nevienlīdzību risināšanai, kas nesatur nezināmos. Programmā ir šādas teorēmas trīs skaitļu attiecībām:

• ja< B то A–C< B–C;
• ja A> B, tad A - C> B - C.

Tā vietā, lai atņemtu locekļus A - C, varat norādīt jebkuru aritmētisko darbību: saskaitīšanu, reizināšanu vai dalīšanu. Tādējādi kalkulators automātiski parādīs summu, atšķirību, produktu vai frakciju nevienlīdzību.

Secinājums

Reālajā dzīvē nevienlīdzība ir tikpat izplatīta kā vienādojumi. Protams, ikdienas dzīvē zināšanas par nevienlīdzības novēršanu var nebūt vajadzīgas. Tomēr nevienlīdzība un to sistēmas tiek plaši izmantotas lietišķajās zinātnēs. Piemēram, dažādi pasaules ekonomikas problēmu pētījumi tiek reducēti līdz lineāru vai kvadrātveida nevienlīdzību sistēmu apkopošanai un atraisīšanai, un dažas nevienlīdzīgas attiecības kalpo kā nepārprotams veids, kā pierādīt noteiktu objektu esamību. Izmantojiet mūsu programmas, lai atrisinātu lineāro nevienlīdzību vai pārbaudītu savus aprēķinus.

Atstarpes metode- vienkāršs veids, kā atrisināt frakcionāli racionālu nevienlīdzību. Tas ir nevienlīdzības nosaukums, kas satur racionālas (vai daļēji racionālas) izteiksmes, kas ir atkarīgas no mainīgā.

1. Apsveriet, piemēram, šādu nevienlīdzību

Intervāla metode ļauj to atrisināt pāris minūtēs.

Šīs nevienlīdzības kreisajā pusē ir daļēja racionāla funkcija. Racionāli, jo tajā nav sakņu, sinusu, logaritmu - tikai racionālas izteiksmes. Labajā pusē ir nulle.

Intervāla metode ir balstīta uz šādu daļējas racionālas funkcijas īpašību.

Daļēja racionālā funkcija var mainīt zīmi tikai tajos punktos, kur tā ir vienāda ar nulli vai nepastāv.

Atgādināsim, kā kvadrātveida trinoms tiek sadalīts faktoros, tas ir, formas izpausmē.

Kur un kur ir kvadrātvienādojuma saknes.

Uzzīmējiet asi un novietojiet punktus, kuros pazūd skaitītājs un saucējs.

Saucēja nulles un ir caurdurti punkti, jo šajos punktos nevienlīdzības kreisajā pusē esošā funkcija nav definēta (jūs nevarat dalīt ar nulli). Skaitītāju nulles un - ir aizpildītas, jo nevienlīdzība nav stingra. Par un mūsu nevienlīdzība ir apmierināta, jo abas tās puses ir vienādas ar nulli.

Šie punkti sadala asi intervālos.

Katrā no šiem intervāliem definēsim frakcionāli racionālās funkcijas zīmi mūsu nevienlīdzības kreisajā pusē. Mēs atceramies, ka daļēji racionāla funkcija var mainīt zīmi tikai tajos punktos, kur tā ir vienāda ar nulli vai nepastāv. Tas nozīmē, ka katrā no intervāliem starp punktiem, kur skaitītājs vai saucējs pazūd, izteiksmes zīme nevienlīdzības kreisajā pusē būs nemainīga - vai nu "plus", vai "mīnus".

Tāpēc, lai noteiktu funkcijas zīmi katrā šādā intervālā, mēs ņemam jebkuru punktu, kas pieder šim intervālam. Tas, kas mums ir ērts.
... Veikt, piemēram, un pārbaudīt izteiksmes zīmi nevienlīdzības kreisajā pusē. Katra no "iekavām" ir negatīva. Kreisajā pusē ir zīme.

Nākamais posms :. Pārbaudīsim, vai nav zīmes. Mēs saprotam, ka kreisā puse ir nomainījusi zīmi uz.

Paņemsim. Ja izteiksme ir pozitīva, tā ir pozitīva visā intervālā no līdz.

Jo nevienlīdzības kreisā puse ir negatīva.

Visbeidzot, class = "tex" alt = "(! LANG: x> 7"> . Подставим и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .!}

Mēs noskaidrojām, kādos intervālos izteiksme ir pozitīva. Atliek pierakstīt atbildi:

Atbilde :.

Lūdzu, ņemiet vērā, ka atstarpēs rakstzīmes mainās. Tas notika tāpēc, ka ejot cauri katram punktam, precīzi viens no lineārajiem faktoriem mainīja zīmi, bet pārējie to nemainīja.

Mēs redzam, ka atstarpes metode ir ļoti vienkārša. Lai atrisinātu frakcionāli racionālo nevienlīdzību ar intervāla metodi, mēs to novedam pie formas:

Or class = "tex" alt = "(! LANG: \ genfrac () () () () (0) (\ displaystyle P \ left (x \ right)) (\ displaystyle Q \ left (x \ right))> 0"> !} vai.

(pa kreisi - daļēja racionāla funkcija, pa labi - nulle).

Tad - uz ciparu līnijas atzīmējam punktus, kuros pazūd skaitītājs vai saucējs.
Šie punkti sadala visu skaitļu līniju intervālos, uz kuriem katra racionālā funkcija saglabā savu zīmi.
Atliek tikai uzzināt tā zīmi katrā intervālā.
Mēs to darām, pārbaudot izteiksmes zīmi jebkurā punktā, kas pieder dotajam intervālam. Pēc tam mēs pierakstām atbildi. Tas ir viss.

Bet rodas jautājums: vai zīmes vienmēr mainās? Nē ne vienmēr! Jāuzmanās, lai zīmes netiktu izvietotas mehāniski un nepārdomāti.

2. Apsvērsim vēl vienu nevienlīdzību.

Class = "tex" alt = "(! LANG: \ genfrac () () () () (0) (\ displaystyle \ left (x-2 \ right) ^ 2) (\ displaystyle \ left (x-1 \ right) \ pa kreisi (x-3 \ pa labi))> 0"> !}

Atkal novietojiet punktus uz ass. Punkti un tiek izsisti, jo tie ir saucēja nulles. Punkts ir arī caurdurts, jo nevienlīdzība ir stingra.

Ja skaitītājs ir pozitīvs, abi faktori saucējā ir negatīvi. To var viegli pārbaudīt, ņemot, piemēram, jebkuru skaitli no noteiktā intervāla. Kreisajā pusē ir zīme:

Kad skaitītājs ir pozitīvs; pirmais faktors saucējā ir pozitīvs, otrais - negatīvs. Kreisajā pusē ir zīme:

Situācija ir tāda pati! Skaitītājs ir pozitīvs, pirmais faktors saucējā ir pozitīvs, otrais ir negatīvs. Kreisajā pusē ir zīme:

Visbeidzot, ar class = "tex" alt = "(! LANG: x> 3"> все множители положительны, и левая часть имеет знак :!}

Atbilde :.

Kāpēc tika izjaukta zīmju maiņa? Jo, ejot cauri punktam, faktors par to ir "atbildīgs" nemainīja zīmi... Līdz ar to arī visa mūsu nevienlīdzības kreisā puse nav mainījusi savu zīmi.

Izeja: ja lineārais koeficients ir vienmērīgā jaudā (piemēram, kvadrātā), tad, izejot caur punktu, izteiksmes zīme kreisajā pusē nemainās... Nepāra pakāpes gadījumā zīme, protams, mainās.

3. Apsvērsim sarežģītāku gadījumu. Tas atšķiras no iepriekšējā ar to, ka nevienlīdzība nav stingra:

Kreisā puse ir tāda pati kā iepriekšējā uzdevumā. Zīmju attēls būs tāds pats:

Varbūt atbilde būs tāda pati? Nē! Tiek pievienots risinājums. Tas ir tāpēc, ka nevienlīdzības kreisajai un labajai pusei ir vienāda ar nulli - tāpēc šis punkts ir risinājums.

Atbilde :.

Matemātikas eksāmena uzdevumā šī situācija bieži sastopama. Šeit pretendenti nonāk slazdā un zaudē punktus. Esi uzmanīgs!

4. Ko darīt, ja skaitītāju vai saucēju nevar linearizēt? Apsveriet šo nevienlīdzību:

Kvadrātveida trinomu nevar diferencēt: diskriminants ir negatīvs, nav sakņu. Bet tas ir labi! Tas nozīmē, ka izteiksmes zīme visiem ir vienāda un konkrēti tā ir pozitīva. Jūs varat uzzināt vairāk par to rakstā par kvadrātiskās funkcijas īpašībām.

Un tagad mēs varam sadalīt savas nevienlīdzības abas puses ar vērtību, kas ir pozitīva visiem. Mēs nonākam līdzvērtīgā nevienlīdzībā:

Kas ir viegli atrisināms ar intervālu metodi.

Lūdzu, ņemiet vērā - mēs sadalījām abas nevienlīdzības puses ar summu, par kuru mēs droši zinājām, ka tā ir pozitīva. Protams, vispārīgā gadījumā nevienlīdzību nav vērts reizināt vai dalīt ar mainīgo, kura zīme nav zināma.

5 ... Apsveriet vēl vienu, šķietami diezgan vienkāršu nevienlīdzību:

Es tikai gribu to reizināt ar. Bet mēs jau esam gudri, un mēs to nedarīsim. Galu galā tas var būt gan pozitīvs, gan negatīvs. Un mēs zinām, ka, ja abas nevienlīdzības puses tiek reizinātas ar negatīvu vērtību, nevienlīdzības zīme mainās.

Mēs darīsim citādi - visu apkoposim vienā daļā un novedīsim pie kopsaucēja. Nulle paliks labajā pusē:

Class = "tex" alt = "(! LANG: \ genfrac () () () () (0) (\ displaystyle x-2) (\ displaystyle x)> 0"> !}

Un pēc tam - mēs pieteiksimies intervāla metode.

Rakstā mēs to apsvērsim nevienlīdzības risināšana... Mēs jums to pateiksim pieejamā veidā kā izveidot nevienlīdzības risinājumu, ar skaidriem piemēriem!

Pirms izskatīsim nevienlīdzības risinājumu, izmantojot piemērus, sapratīsim pamatjēdzienus.

Vispārīga informācija par nevienlīdzību

Nevienlīdzība sauc par izteicienu, kurā funkcijas ir saistītas ar relācijas zīmēm> ,. Nevienlīdzība ir gan skaitliska, gan alfabētiska.
Nevienlīdzību ar divām attiecību pazīmēm sauc par dubultām, ar trim - par trīskāršām utt. Piemēram:
a (x)> b (x),
a (x) a (x) b (x),
a (x) b (x).
a (x) Nevienlīdzība, kas satur zīmi> vai nav stingra.
Nevienlīdzības risināšana ir jebkura izmaiņu vērtība, pie kuras šī nevienlīdzība ir patiesa.
"Atrisiniet nevienlīdzību"nozīmē, ka ir jāatrod daudzi no visiem tā risinājumiem. Ir dažādi metodes nevienlīdzības risināšanai... Priekš nevienlīdzības risinājumi izmantojiet ciparu līniju, kas ir bezgalīga. Piemēram, nevienlīdzības risinājums x> 3 ir intervāls no 3 līdz +, un skaitlis 3 nav iekļauts šajā intervālā, tāpēc punktu taisnā līnijā apzīmē ar tukšu apli, jo nevienlīdzība ir stingra.
+
Atbilde būs: x (3; +).
Vērtība x = 3 nav iekļauta risinājumu komplektā, tāpēc iekavas ir apaļas. Bezgalības zīmi vienmēr ieskauj iekavas. Zīme nozīmē "piederība".
Apsvērsim, kā novērst nevienlīdzību, izmantojot citu parakstītu piemēru:
x 2
-+
Vērtība x = 2 ir iekļauta risinājumu komplektā, tāpēc kvadrātiekavu un punktu uz līnijas norāda aizpildīts aplis.
Atbilde būs: x)