Théorie des nombres complexes et exemples. Nombres complexes
Nombres complexes
Imaginaire et nombres complexes. Abscisse et ordonnée
nombre complexe. Conjuguer les nombres complexes.
Opérations avec des nombres complexes. Géométrique
représentation des nombres complexes. avion complexe.
Module et argument d'un nombre complexe. trigonométrique
forme de nombre complexe. Opérations complexes
nombres sous forme trigonométrique. Formule Moivre.
Informations de base sur imaginaire et nombres complexes sont donnés dans la section "Nombres imaginaires et complexes". Le besoin de ces nombres d'un nouveau type est apparu lors de la résolution d'équations quadratiques pour le cas
ré< 0 (здесь réest le discriminant de l'équation quadratique). Pendant longtemps, ces nombres n'ont pas trouvé d'utilisation physique, c'est pourquoi ils ont été appelés nombres "imaginaires". Cependant, ils sont maintenant très largement utilisés dans divers domaines de la physique.et technologie : génie électrique, hydro- et aérodynamique, théorie de l'élasticité, etc.
Nombres complexes s'écrivent ainsi :un+bi. Ici un et b – nombres réels , un je – unité imaginaire. e. je 2 = –1. Numéro un appelé abscisse, un b - ordonnéenombre complexeun + b.Deux nombres complexesun+bi et a-bi appelé conjuguer nombres complexes.
Principaux accords :
1. Nombre réel
unpeut aussi s'écrire sous la formenombre complexe:un + 0 je ou alors un - 0 je. Par exemple, les entrées 5 + 0je et 5 - 0 jesignifie le même nombre 5 .2. Nombre complexe 0 + biappelé purement imaginaire Numéro. Enregistrementbisignifie la même chose que 0 + bi.
3. Deux nombres complexesun+bi etc + disont considérés comme égaux siun = c et b = ré. Autrement les nombres complexes ne sont pas égaux.
Une addition. La somme des nombres complexesun+bi et c + diest appelé un nombre complexe (a+c ) + (b+d ) je .Ainsi, une fois ajouté les nombres complexes, leurs abscisses et ordonnées sont additionnées séparément.
Cette définition suit les règles de traitement des polynômes ordinaires.
Soustraction. La différence entre deux nombres complexesun+bi(réduit) et c + di(soustrait) est appelé un nombre complexe (a-c ) + (bd ) je .
Ainsi, lors de la soustraction de deux nombres complexes, leurs abscisses et ordonnées sont soustraites séparément.
Multiplication. Le produit de nombres complexesun+bi et c + di est appelé un nombre complexe.
(ac-bd ) + (ad+bc ) je .Cette définition découle de deux exigences :
1) nombres un+bi et c + didevrait se multiplier comme algébrique binômes,
2) nombre jea pour propriété principale :je 2 = – 1.
EXEMPLE ( un + bi )(a-bi) = un 2 +b 2 . Ainsi, travail
deux nombres complexes conjugués est égal au réel
nombre positif.
Division. Diviser un nombre complexeun+bi (divisible) à un autrec + di(séparateur) - signifie trouver le troisième nombree + fi(chat), qui, multiplié par un diviseurc + di, ce qui donne le dividendeun + b.
Si le diviseur n'est pas nul, la division est toujours possible.
EXEMPLE Trouver (8+je ) : (2 – 3 je) .
Solution Réécrivons ce rapport sous forme de fraction :
Multiplier son numérateur et son dénominateur par 2 + 3je
Et après avoir effectué toutes les transformations, on obtient :

Représentation géométrique des nombres complexes. Les nombres réels sont représentés par des points sur la droite numérique :
Voici le point UNsignifie numéro -3, pointB est le nombre 2, et O- zéro. En revanche, les nombres complexes sont représentés par des points sur le plan de coordonnées. Pour cela, nous choisissons des coordonnées rectangulaires (cartésiennes) avec les mêmes échelles sur les deux axes. Alors le nombre complexeun+bi sera représenté par un point P avec abscisse a et ordonnée b (voir fig.). Ce système de coordonnées est appelé avion complexe .

module le nombre complexe est appelé la longueur du vecteurOP, représentant un nombre complexe sur la coordonnée ( intégré) avion. Module des nombres complexesun+bi désigné par | un+bi| ou lettre r
Plan de cours.
1. Moment organisationnel.
2. Présentation du matériel.
3. Devoirs.
4. Résumer la leçon.
Pendant les cours
I. Moment organisationnel.
II. Présentation du matériel.
Motivation.
L'expansion de l'ensemble des nombres réels consiste dans le fait que de nouveaux nombres (imaginaires) sont ajoutés aux nombres réels. L'introduction de ces nombres est liée à l'impossibilité d'extraire la racine d'un nombre négatif dans l'ensemble des nombres réels.
Introduction de la notion de nombre complexe.
Les nombres imaginaires avec lesquels on complète les nombres réels s'écrivent bi, où je est l'unité imaginaire, et je 2 = - 1.
Sur cette base, nous obtenons la définition suivante d'un nombre complexe.
Définition. Un nombre complexe est une expression de la forme un+bi, où un et b sont des nombres réels. Dans ce cas, les conditions suivantes sont remplies :
a) Deux nombres complexes une 1 + b 1 je et une 2 + b 2 jeégal si et seulement si une 1 = une 2, b1=b2.
b) L'addition des nombres complexes est déterminée par la règle :
(une 1 + b 1 je) + (une 2 + b 2 je) = (une 1 + une 2) + (b 1 + b 2) je.
c) La multiplication des nombres complexes est déterminée par la règle :
(a 1 + b 1 je) (a 2 + b 2 je) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) je.
Forme algébrique d'un nombre complexe.
Écrire un nombre complexe sous la forme un+bi est appelée la forme algébrique d'un nombre complexe, où un- partie réelle bi est la partie imaginaire, et b est un nombre réel.
Nombre complexe un+bi est considéré égal à zéro si ses parties réelle et imaginaire sont égales à zéro : un=b=0
Nombre complexe un+bià b = 0 considéré comme un nombre réel un: un + 0i = un.
Nombre complexe un+bià un = 0 est dit purement imaginaire et est noté bi: 0 + bi = bi.
Deux nombres complexes z = a + bi et = un - bi, qui ne diffèrent que par le signe de la partie imaginaire, sont dits conjugués.
Actions sur les nombres complexes sous forme algébrique.
Les opérations suivantes peuvent être effectuées sur des nombres complexes sous forme algébrique.
1) Ajout.
Définition. La somme des nombres complexes z 1 = une 1 + b 1 je et z 2 = une 2 + b 2 je appelé un nombre complexe z, dont la partie réelle est égale à la somme des parties réelles z1 et z2, et la partie imaginaire est la somme des parties imaginaires des nombres z1 et z2, c'est à dire z = (une 1 + une 2) + (b 1 + b 2)i.
Nombres z1 et z2 sont appelés termes.
L'addition des nombres complexes a les propriétés suivantes :
1º. Commutativité: z1 + z2 = z2 + z1.
2º. Associativité : (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).
3º. Nombre complexe -a -bi est appelé l'opposé d'un nombre complexe z = a + bi. Nombre complexe opposé au nombre complexe z, noté -z. Somme de nombres complexes z et -z est égal à zéro : z + (-z) = 0
Exemple 1 : Ajouter (3 - je) + (-1 + 2i).
(3 - je) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) je = 2 + 1i.
2) Soustraction.
Définition. Soustraire d'un nombre complexe z1 nombre complexe z2 z, quelle z + z 2 = z 1.
Théorème. La différence des nombres complexes existe et, de plus, est unique.
Exemple 2 : soustraire (4 - 2i) - (-3 + 2i).
(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) je = 7 - 4i.
3) Multiplication.
Définition. Le produit de nombres complexes z 1 =a 1 +b 1 je et z 2 \u003d une 2 + b 2 je appelé un nombre complexe z, défini par l'égalité : z = (une 1 une 2 – b 1 b 2) + (une 1 b 2 + une 2 b 1)i.
Nombres z1 et z2 sont appelés facteurs.
La multiplication des nombres complexes a les propriétés suivantes :
1º. Commutativité: z 1 z 2 = z 2 z 1.
2º. Associativité : (z 1 z 2)z 3 = z 1 (z 2 z 3)
3º. Distributivité de la multiplication par rapport à l'addition :
(z 1 + z 2) z 3 \u003d z 1 z 3 + z 2 z 3.
4º. z \u003d (a + bi) (a - bi) \u003d a 2 + b 2 est un nombre réel.
En pratique, la multiplication des nombres complexes s'effectue selon la règle de multiplication de la somme par la somme et de séparation des parties réelle et imaginaire.
Dans l'exemple suivant, considérons la multiplication de nombres complexes de deux manières : par la règle et en multipliant la somme par la somme.
Exemple 3 : multiplier (2 + 3i) (5 – 7i).
1 voie. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15 )je = 31 + je.
2 voies. (2 + 3i) (5 - 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 - 14i + 15i + 21 = 31 + je.
4) Division.
Définition. Diviser un nombre complexe z1à un nombre complexe z2, signifie trouver un tel nombre complexe z, quelle z z 2 = z 1.
Théorème. Le quotient de nombres complexes existe et est unique si z2 ≠ 0 + 0i.
En pratique, le quotient des nombres complexes se trouve en multipliant le numérateur et le dénominateur par le conjugué du dénominateur.
Laisser être z 1 = une 1 + b 1 je, z 2 = une 2 + b 2 je, alors



 .
.
Dans l'exemple suivant, nous effectuons la division par la formule et la règle de multiplication par le conjugué du dénominateur.
Exemple 4. Trouver un quotient  .
.
5) Élever à une puissance entière positive.
a) Pouvoirs de l'unité imaginaire.
Profitant de l'égalité je 2 \u003d -1, il est facile de définir toute puissance entière positive de l'unité imaginaire. Nous avons:
je 3 \u003d je 2 je \u003d -je,
je 4 \u003d je 2 je 2 \u003d 1,
je 5 \u003d je 4 je \u003d je,
je 6 \u003d je 4 je 2 \u003d -1,
je 7 \u003d je 5 je 2 \u003d -je,
je 8 = je 6 je 2 = 1 etc.
Cela montre que les valeurs des degrés dans, où n- un entier positif, répété périodiquement lorsque l'indicateur augmente de 4 .
Par conséquent, pour augmenter le nombre jeà une puissance entière positive, diviser l'exposant par 4 et dressé jeà la puissance dont l'exposant est le reste de la division.
Exemple 5 Calculez : (je 36 + je 17) je 23.
je 36 = (je 4) 9 = 1 9 = 1,
je 17 = je 4 × 4+1 = (je 4) 4 × je = 1 je = je.
je 23 = je 4 × 5+3 = (je 4) 5 × je 3 = 1 je 3 = - je.
(je 36 + je 17) je 23 \u003d (1 + je) (- je) \u003d - je + 1 \u003d 1 - je.
b) L'élévation d'un nombre complexe à une puissance entière positive s'effectue selon la règle d'élévation d'un binôme à la puissance correspondante, puisqu'il s'agit d'un cas particulier de multiplication de facteurs complexes identiques.
Exemple 6 Calculez : (4 + 2i) 3
(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.
Les nombres complexes sont une extension minimale de l'ensemble des nombres réels qui nous sont familiers. Leur différence fondamentale est qu'un élément apparaît qui au carré donne -1, c'est-à-dire je, ou .
Tout nombre complexe a deux parties : réel et imaginaire:
Ainsi, il est clair que l'ensemble des nombres réels coïncide avec l'ensemble des nombres complexes à partie imaginaire nulle.
Le modèle le plus populaire pour l'ensemble des nombres complexes est le plan ordinaire. La première coordonnée de chaque point sera sa partie réelle et la seconde - imaginaire. Ensuite, le rôle des nombres complexes eux-mêmes sera des vecteurs commençant au point (0,0).
Opérations sur les nombres complexes.
En effet, si l'on prend en compte le modèle de l'ensemble des nombres complexes, il est intuitivement clair que l'addition (soustraction) et la multiplication de deux nombres complexes s'effectuent de la même manière que les opérations correspondantes sur les vecteurs. De plus, nous entendons le produit croisé des vecteurs, car le résultat de cette opération est à nouveau un vecteur.
1.1 Ajout.
(Comme vous pouvez le voir, cette opération correspond exactement à )
1.2 Soustraction, de même, s'effectue selon la règle suivante :
2. Multiplication.

3. Division.
Il est défini simplement comme l'opération inverse de la multiplication.

forme trigonométrique.
Le module d'un nombre complexe z est la quantité suivante :
 ,
,
il est évident qu'il s'agit encore une fois simplement du module (longueur) du vecteur (a,b).
Le plus souvent, le module d'un nombre complexe est noté ρ.
Il se trouve que
z = ρ(cosφ+isinφ).

Ce qui suit découle directement de la forme trigonométrique d'écriture d'un nombre complexe. formules :
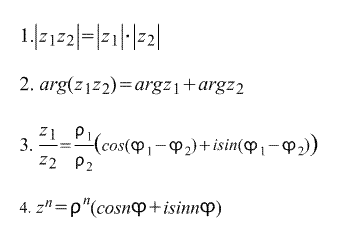
La dernière formule s'appelle Formule De Moivre. La formule en découle directement. nième racine d'un nombre complexe:

ainsi, il y a n nièmes racines du nombre complexe z.