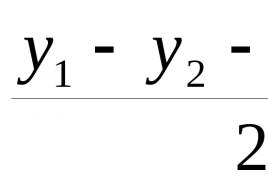Ülejäänud jagamine 45-ga. Ülejäänud täisarvude jagamine, reeglid, näited
Selles artiklis me analüüsime täisarvude jagamine ülejäänuga... Alustame täisarvude jagamise üldpõhimõttest, sõnastame ja tõestame jääkidega täisarvude jagatavuse teoreemi, jälgime seoseid dividendi, jagaja, mittetäieliku jagaja ja ülejäänud vahel. Järgmisena hääletame reegleid, mille järgi tehakse täisarvude jagamine ülejäänuga, ja kaalume näidete lahendamisel nende reeglite rakendamist. Pärast seda õpime, kuidas kontrollida ülejäänud arvude jagamise tulemust.
Lehe navigeerimine.
Täisarvude jaotuse mõistmine ülejäänuga
Arvestame ülejäänud täisarvude jagamist üldise jagunemisega ülejäänud looduslike arvudega. See on tingitud asjaolust, et looduslikud arvud on täisarvude lahutamatu osa.
Alustame kirjelduses kasutatud mõistetest ja nimetustest.
Analoogia põhjal looduslike arvude jagamisega jäägiga eeldame, et kahe täisarvu a ja b (b ei ole nulliga) jäägiga jagamise tulemus on kaks täisarvu c ja d. Numbreid a ja b kutsutakse jagatav ja eraldaja vastavalt arv d - meeldetuletus jagades a b-ga, nimetatakse täisarvu c mittetäielik privaatne (või lihtsalt privaatnekui ülejäänud on null).
Olgem nõus eeldama, et ülejäänud osa on mitte-negatiivne täisarv ja selle väärtus ei ületa b, see tähendab (me kohtasime selliseid ebavõrdsuse ahelaid, kui rääkisime kolme või enama täisarvu võrdlemisest).
Kui arv c on mittetäielik jagatis ja arv d on täisarvu a jagamise täisarvuga b, siis kirjutame selle fakti lühidalt vormi a võrdusena: b \u003d c (ülejäänud d).
Pange tähele, et täisarvu a jagamisel täisarvuga b võib ülejäänud olla null. Sel juhul öeldakse, et a jagub b-ga ilma jääkideta (või täielikult). Seega on täisarvude jagamine ilma jäägita täisarvude jagamise erijuht.
Samuti tasub öelda, et nulli jagamisel mõne täisarvuga tegeleme alati jagamiseta ilma jäägita, kuna sel juhul on jagatis null (vt nulli täisarvuga jagamise teooriat käsitlevat jaotist) ja ka ülejäänud on null.
Oleme otsustanud terminoloogia ja nimetused, nüüd selgitame välja täisarvude jagamise tähenduse jäägiga.
Negatiivse täisarvu a jagamine positiivse täisarvuga b võib samuti olla mõttekas. Selleks pidage negatiivseks täisarvuks võlga. Kujutame ette järgmist olukorda. Võlg, mis on kirjed, peab tasuma b inimest, kes teeb sama sissemakse. Mittetäieliku jagatise c absoluutväärtus määrab antud juhul iga inimese võla suuruse ja ülejäänud d näitab, mitu eset jääb pärast võla tasumist. Toome näite. Oletame, et 2 inimest vajab 7 õuna. Kui eeldame, et kumbki on võlgu 4 õuna, siis pärast võla tasumist on neil 1 õun. See olukord vastab võrdsusele (−7): 2 \u003d −4 (ülejäänud 1).
Me ei anna suvalise täisarvu a ülejäänud osa jagamisele negatiivse täisarvuga mingit tähendust, kuid jätame sellele õiguse eksisteerida.
Ülejäänud täisarvude jagatavuse teoreem
Kui me rääkisime loodusarvude jagamisest ülejäänuga, saime teada, et dividend a, jagaja b, mittetäielik jagatis c ja ülejäänud d on seotud võrdsusega a \u003d b c + d. Täisarvudel a, b, c ja d on sama seos. Selle ühenduse kiidavad heaks järgmised ülejäänud jagatavuse teoreem.
Teoreem.
Mis tahes täisarvu a saab ainulaadselt esitada täis- ja nullarvu b kujul kujul a \u003d b q + r, kus q ja r on mõned täisarvud ja.
Tõendid.
Kõigepealt tõestame a \u003d b q + r esindamise võimalust.
Kui täisarvud a ja b on sellised, et a jagub b-ga ühtlaselt, siis definitsiooni järgi on olemas täisarv q, nii et a \u003d b q. Sel juhul kehtib võrdsus a \u003d b q + r r \u003d 0 korral.
Nüüd eeldame, et b on positiivne täisarv. Valige täisarv q nii, et korrutis b q ei ületaks a ja korrutis b (q + 1) oleks juba suurem kui a. See tähendab, et võtame q nii, et ebavõrdsused b q Jääb tõestada võimalust tähistada a \u003d b q + r negatiivse b korral. Kuna arvu b moodul on antud juhul positiivne arv, siis on olemas kujutis, kus q 1 on mingi täisarv ja r on tingimustele vastav täisarv. Seejärel, võttes q \u003d −q 1, saame negatiivse b jaoks vajaliku esituse a \u003d b q + r. Läheme üle ainulaadsuse tõestusele. Oletame, et lisaks esitusele a \u003d bq + r on q ja r täisarvud ja veel üks esitus a \u003d bq 1 + r 1, kus q 1 ja r 1 on mõned täisarvud ja q 1 ≠ q ja. Pärast esimese võrduse vasaku ja parema külje lahutamist teise võrdsuse vasakust ja paremast küljest saame 0 \u003d b (q - q 1) + r - r 1, mis on võrdne võrdsusega r - r 1 \u003d b (q 1 - q) ... Siis vormi võrdsus Tingimuste põhjal ja võime sellest järeldada. Kuna q ja q 1 on täisarvud ja q ≠ q 1, siis järeldame sellest Võrdsus a \u003d b c + d võimaldab teil leida tundmatu dividendi a, kui teate jagajat b, mittetäielikku jagajat c ja ülejäänud d. Vaatame ühte näidet. Näide. Mis on dividend, kui selle jagamisel täisarvuga −21 saadakse mittetäielik jagatis 5 ja ülejäänud 12? Otsus. Peame arvutama dividendi a, kui teame jagajat b \u003d −21, osalist jagajat c \u003d 5 ja ülejäänud d \u003d 12. Pöördudes võrdsuse a \u003d b c + d juurde, saame a \u003d (- 21) 5 + 12. Vaadeldes korrutame kõigepealt täisarvud −21 ja 5 vastavalt erinevate märkidega täisarvude korrutamise reeglile, mille järel lisame erinevate märkidega täisarvud: (−21) 5 + 12 \u003d −105 + 12 \u003d −93. Vastus: −93
.
Seoseid dividendi, jagaja, mittetäieliku jagaja ja ülejäägi vahel väljendavad ka vormi b \u003d (a - d) võrdused: c, c \u003d (a - d): b ja d \u003d a - b · c. Need võrdused võimaldavad arvutada vastavalt jagajat, osalist jagatist ja ülejäänud osa. Tihti peame leidma täisarvu a jagamise täisarvuga b, kui dividend, jagaja ja osaline jagatis on teada, kasutades valemit d \u003d a - b · c. Lisaküsimuste vältimiseks vaatame ülejäänu arvutamise näidet. Näide. Leidke ülejäänud arv jagades täisarvu −19 täisarvuga 3, kui teate, et osaline jagatis on −7. Otsus. Jaotuse ülejäänud osa arvutamiseks kasutame valemit kujul d \u003d a - b · c. Tingimusest on meil olemas kõik vajalikud andmed a \u003d −19, b \u003d 3, c \u003d −7. Saame d \u003d a - b c \u003d −19−3 (−7) \u003d −19 - (- 21) \u003d - 19 + 21 \u003d 2 (vahe −19 - (- 21), mille arvutame negatiivse täisarvu lahutamise reegliga ). Vastus: Nagu oleme korduvalt märkinud, on positiivsed täisarvud loomulikud arvud. Seetõttu jagatakse ülejäänud positiivsete täisarvudega jagamine vastavalt kõigile jagunemisreeglitele ülejäänud looduslike arvudega. On väga oluline, et jagamist saaks hõlpsalt teostada ülejäänud naturaalsete arvudega, sest just see on aluseks mitte ainult positiivsete täisarvude jagamisele, vaid ka kõigi jagunemisreeglite alusele ülejäänud suvaliste täisarvudega. Meie vaatenurgast on kõige mugavam teostada pikka jagamist, see meetod võimaldab teil saada nii mittetäielikku jagatist (või lihtsalt jagatist) kui ka ülejäänud. Mõelgem jagamise näite ülejäänud positiivsete täisarvudega. Näide. Jagage 14 671 ülejäänud osaga 54-ga. Otsus. Jagame need positiivsed täisarvud veeruga: Osaline jagatis osutus 271 ja ülejäänud on 37. Vastus: 14 671: 54 \u003d 271 (ülejäänud 37). Koostame reegli, mis võimaldab jagamist positiivse täisarvu ülejäänud osaga negatiivse täisarvuga. Mittetäielik jagatis positiivse täisarvu a jagamisel negatiivse täisarvuga b on vastupidine mittetäielikule jagamisele jagatis a b mooduliga ja ülejäänud jagamine a b abil võrdub jagamise ülejäänud osaga. Sellest reeglist järeldub, et mittetäielik jagatis positiivse täisarvu jagamisel negatiivse täisarvuga on mitte-positiivne täisarv. Uuendame väljakuulutatud reegli jagamise algoritmiks ülejäänud positiivse täisarvu negatiivse täisarvuga: Toome näite positiivse täisarvu jagamiseks negatiivse täisarvuga algoritmi kasutamisest. Näide. Jagage positiivne täisarv 17 negatiivse täisarvuga −5. Otsus. Kasutame jagamise algoritmi positiivse täisarvu negatiivse täisarvuga. Jagamine 3 vastand on −3. Seega on soovitud jagamine 17 jagamisel −5-ga −3 ja ülejäänud on 2. Vastus: 17: (- 5) \u003d - 3 (ülejäänud 2). Näide. Jaga 45 kuni -15. Otsus. Dividendi ja jagaja moodulid on vastavalt 45 ja 15. Arv 45 jagub 15-ga ilma jäägita, samas kui jagatis on 3. Seetõttu on positiivne täisarv 45 jagatav negatiivse täisarvuga −15 ilma jäägita ja jagatis on võrdne vastandarvuga 3, see tähendab −3. Tõepoolest, vastavalt erinevate märkidega täisarvude jagamise reeglile meil on. Vastus: 45:(−15)=−3
.
Andkem jagamisreegli sõnastus negatiivse täisarvu positiivse täisarvu ülejäänud osaga. Et saada mittetäielik jagatis c negatiivse täisarvu a jagamisest positiivse täisarvuga b, peate mittetäieliku jagatisega vastandama algarvude moodulite jagamise ja sellest ühe lahutama, seejärel arvutama ülejäänud d valemiga d \u003d a - b c. Sellest jäägiga jagamise reeglist järeldub, et negatiivse täisarvu jagamise positiivse täisarvuga mittetäielik jagatis on negatiivne täisarv. Kõlatud reeglist tuleneb jagamisalgoritm negatiivse täisarvu a positiivse täisarvu b ülejäänud osaga: Analüüsime näite lahendust, milles kasutame ülejäänud jaotusega kirjalikku jagamisalgoritmi. Näide. Leidke mittetäielik jagatis ja negatiivse täisarvu -17 jagatud positiivse täisarvuga 5. Otsus. Dividendi −17 moodul on 17 ja jagaja 5 moodul on 5. Jagamine 17 5-ga saame mittetäieliku jagaja 3 ja ülejäänud 2. 3 vastand on −3. Lahutage üks hulgast −3: −3−1 \u003d −4. Niisiis, nõutav mittetäielik jagatis on −4. Jääb ülejäänu arvutada. Meie näites a \u003d −17, b \u003d 5, c \u003d −4, siis d \u003d a - b c \u003d −17−5 (−4) \u003d −17 - (- 20) \u003d - 17 + 20 \u003d 3 ... Seega on negatiivse täisarvu -17 jagamise positiivse täisarvuga 5 osaline jagatis -4 ja ülejäänud on 3. Vastus: (−17): 5 \u003d −4 (ülejäänud 3). Näide. Jagage negatiivne täisarv -1404 positiivse täisarvuga 26. Otsus. Dividendi moodul on 1 404, jagaja moodul on 26. Jagage 1 404 veeruga 26-ga: Kuna dividendi moodul jagati jagaja mooduliga ilma jäägita, on algsed täisarvud jagatavad ilma jäägita ja soovitud jagatis võrdub arvuga, mis on vastupidine 54-le, see tähendab −54. Vastus: (−1 404):26=−54
.
Koostame jagamisreegli ülejäänud negatiivsete täisarvudega. Mittetäieliku jagatise c saamiseks negatiivse täisarvu a jagamisel täisarvu negatiivse arvuga b peate arvutama mittetäieliku jagatise algarvude moodulite jagamisest ja lisama sellele ühe, seejärel arvutama ülejäänud d valemiga d \u003d a - b c. Sellest reeglist järeldub, et negatiivsete täisarvude jagamise mittetäielik jagatis on positiivne täisarv. Kirjutame määratud reegli negatiivsete täisarvude jagamise algoritmina ümber: Kaaluge näite lahendamisel negatiivsete täisarvude jagamise algoritmi kasutamist. Näide. Leidke negatiivse täisarvu -17 jagamise ja negatiivse täisarvu -5 jagamise osaline jagatis. Otsus. Kasutame sobivat mooduljaotuse algoritmi. Dividendi moodul on 17, jagaja moodul on 5. Jaoskond 17 by 5 annab mittetäieliku jagatise 3 ja ülejäänud 2. Lisage üks mittetäielikule jagatisele 3: 3 + 1 \u003d 4. Seetõttu on nõutav mittetäielik jagatis −17 −5 jagamisel 4. Jääb ülejäänu arvutada. Selles näites a \u003d −17, b \u003d −5, c \u003d 4, siis d \u003d a - b c \u003d −17 - (- 5) 4 \u003d −17 - (- 20) \u003d - 17 + 20 \u003d 3 ... Seega on negatiivse täisarvu -17 jagamise negatiivse täisarvuga -5 mittetäielik jagatis 4 ja ülejäänud 3. Vastus: (−17): (- 5) \u003d 4 (ülejäänud 3). Pärast täisarvude jagamist ülejäänuga on kasulik tulemust kontrollida. Kontroll viiakse läbi kahes etapis. Esimeses etapis kontrollitakse, kas ülejäänud d on mitte-negatiivne arv, ja kontrollitakse ka seisukorda. Kui kõik kontrollimise esimese etapi tingimused on täidetud, võite minna kontrollimise teise etapi juurde, vastasel juhul võib väita, et ülejäänud osas jagamise ajal tehti viga. Teises etapis kontrollitakse võrdsuse a \u003d b c + d kehtivust. Kui see võrdsus on tõsi, siis jagamine ülejäänuga toimus õigesti, vastasel juhul tehti kusagil viga. Vaatleme lahendusi näidetest, kus kontrollitakse ülejäänud arvudega täisarvude jagamise tulemust. Näide. Kui jagate numbri −521 arvuga −12, saate mittetäieliku jagatise 44 ja ülejäänud 7, kontrollige tulemust. Otsus. −2 b \u003d −3 jaoks, c \u003d 7, d \u003d 1. Meil on b c + d \u003d −3 7 + 1 \u003d −21 + 1 \u003d −20... Seega on võrdsus a \u003d b c + d vale (meie näites a \u003d −19). Seetõttu tehti jagamine ülejäänud osas valesti. Numbrite jagatavuse testid- need on reeglid, mis võimaldavad ilma jagamist tegemata suhteliselt kiiresti teada saada, kas see arv jagub antud arvuga ilma ülejäänuteta. See on üks lihtsamaid jagatavuse kriteeriume. See kõlab järgmiselt: kui loodusliku numbri salvestamine lõpeb paarisarvuga, siis on see paariline (jagub kahega ilma jäägita) ja kui numbri salvestamine lõpeb paaritu numbriga, siis on see arv paaritu. Sellel jagamiskriteeriumil on täiesti erinevad reeglid: kui numbri arvude summa jagub 3-ga, siis arv jagub ka 3-ga; kui numbri arvude summa ei ole jagatav 3-ga, siis ei ole ka number 3-ga jagatav. See jagatavuse kriteerium on keerulisem. Kui numbri viimased 2 numbrit moodustavad 4-ga jagatava arvu või on 00, siis number jagub 4-ga, vastasel juhul ei saa see arv jäägita 4-ga jagada. Ja jällegi on meil üsna lihtne jagamismärk: kui loodusliku numbri kirje lõpeb numbriga 0 või 5, siis see arv jagub ilma jäägita 5-ga. Kui numbri kirje lõpeb teise numbriga, siis ei ole see arv jagatav 5-ga ilma jäägita. Meie ees on liitarv 6, mis on arvude 2 ja 3 korrutis. Seetõttu on jagatavus 6-ga ka liitliit: selleks, et arv saaks jagada 6-ga, peab see üheaegselt vastama kahele jagamistunnusele: jagamistunnus 2-ga ja jagamistunnus 3-ga. Samal ajal pange tähele, et sellisel liitarvul nagu 4 on jagamise individuaalne märk, sest see on iseenesest arvu 2 korrutis. Aga tagasi jagatavuse 6 kriteeriumi järgi. See jagamismärk on keerulisem: arv jagub 7-ga, kui selle arvu kümnetest viimase kahekordistatud numbri lahutamise tulemus jagub 7-ga või võrdub 0-ga. Jaguvus 8-ga on järgmine: kui viimased 3 numbrit moodustavad arvu, mis jagub 8-ga või 000-ga, siis antud arv jagub 8-ga. See jagamismärk sarnaneb jagatavuse märgiga 3: kui numbri arvude summa jagub 9-ga, siis arv jagub ka 9-ga; kui numbri arvude summa ei ole jagatav 9-ga, siis ei ole ka arv 9-ga jagatav. Kombineerisin need jagatavuse märgid, kuna neid saab kirjeldada samamoodi: arv jagatakse bitiühikuga, kui arvu lõpus olevate nullide arv on suurem või võrdne antud bittühikus olevate nullide arvuga. Selleks, et teada saada, kas number jagub 11-ga, peate saama selle arvu paaris- ja paaritu numbri summade vahe. Kui see erinevus on võrdne 0 või jagub 11-ga ilma jäägita, siis arv ise jagub 11-ga ilma jäägita. Number 12 on liit. Selle jagamiskriteeriumiks on vastavus jagamiskriteeriumidele korraga 3-ga ja 4-ga. Jagumise 13-ga märk on see, et kui arvu kümnete arv, mis on liidetud selle arvu ühikute korrutamisel 4-ga, on 13 kordne või võrdne 0-ga, siis arv ise jagub 13-ga. Nagu ülaltoodust nähtub, võime eeldada, et mis tahes loodusarvude jaoks saate valida oma individuaalse jagamiskriteeriumi või "komposiit" funktsiooni, kui number on mitme erineva arvu kordne. Kuid nagu näitab praktika, mida suurem on number, seda keerukam on selle märk. Võimalik, et jagamiskriteeriumi kontrollimiseks kulutatud aeg võib olla võrdne või suurem kui jagamine ise. Seetõttu kasutame tavaliselt kõige lihtsamaid jagatavuse kriteeriume. Artiklis käsitletakse ülejäänud arvude jagamise mõistet. Tõestagem teoreem täisarvude jagatavuse ülejäänuga ja uurigem seoseid dividendide ja jagajate, mittetäielike jagajate ja jääkide vahel. Mõelgem reeglitele, kui tehakse täisarvude jagamine jääkidega, olles üksikasjalikult kaalunud näiteid. Lahenduse lõpus kontrollime. Ülejäänud täisarvude jagunemist peetakse üldistatud jagunemiseks ülejäänud looduslike arvudega. Seda tehakse seetõttu, et looduslikud arvud on täisarvude lahutamatud. Jagamine suvalise arvu ülejäänud osaga tähendab, et täisarv a jagub nullist erineva arvuga b. Kui b \u003d 0, siis ülejäänud jaotust ei tehta. Lisaks looduslike arvude jagamisele ülejäänuga tehakse täisarvude a ja b jagamine c ja d abil, kui b erineb nullist. Sel juhul nimetatakse a ja b dividendiks ja jagajaks ning d on jagamise ülejäänud osa, c on täisarv või mittetäielik jagatis. Kui eeldame, et ülejäänud osa on mitte-negatiivne täisarv, siis pole selle väärtus suurem kui arvu b moodul. Kirjutame nii: 0 ≤ d ≤ b. Seda ebavõrdsuse ahelat kasutatakse 3 või enama arvu võrdlemisel. Kui c on mittetäielik jagatis, siis d on täisarvu a jagamine b-ga, võite lühidalt fikseerida: a: b \u003d c (ülejäänud d). Ülejäänud arvude a jagamisel b-ga on võimalik , siis nad ütlevad, et a jagub b-ga täielikult, st ilma jäägita. Ülejäänud jagamist peetakse jagamise erijuhuks. Kui jagame nulli mõne arvuga, saame tulemuseks nulli. Jaotuse ülejäänud osa on samuti null. Selle taga on nullist täisarvuga jagamise teooria. Vaatame nüüd täisarvude jagamise tähendust jäägiga. On teada, et positiivsed täisarvud on loomulikud, siis jäägiga jagamisel saate sama tähenduse nagu jagades loomulikud arvud ülejäänuga. Negatiivse täisarvu a jagamisel positiivse täisarvuga b on mõistlik. Vaatame ühte näidet. Kujutades ette olukorda, kus meil on kaupade võlg summas a, mille peavad tasuma b inimesed. See nõuab kõigilt sama panust. Igaühe võlasumma kindlaksmääramiseks peate pöörama tähelepanu erasektori suurusele p. Ülejäänud d ütleb, et esemete arv on teada pärast võlgade tasumist. Võtame näite õuntega. Kui 2 inimest vajab 7 õuna. Kui arvestate, et kõik peavad tagastama 4 õuna, on pärast täielikku arvutamist 1 õun. Kirjutagem see võrdsuse kujul: (- 7): 2 \u003d - 4 (o punktiga 1). Mis tahes arvu a jagamine täisarvuga ei ole mõistlik, kuid see on võimalik valikuna. Leidsime, et a on dividend, siis b on jagaja, c on mittetäielik jagatis ja d on ülejäänud. Need on omavahel seotud. Näitame seda seost, kasutades võrdsust a \u003d b c + d. Nende omavahelist seost iseloomustab järelejäänud jagatavuse teoreem. Teoreem Iga täisarvu saab esitada ainult täis- ja nullarvu b kaudu sel viisil: a \u003d b q + r, kus q ja r on mõned täisarvud. Siin on meil 0 ≤ r ≤ b. Tõestagem a \u003d b q + r olemasolu olemasolu. Tõendid Kui on kaks numbrit a ja b ja a jagub b-ga ilma jäägita, tähendab definitsioon, et on olemas number q, mis vastab tõele võrdsusega a \u003d b q. Siis võib võrdsust pidada tõeseks: a \u003d b q + r, kui r \u003d 0. Siis on vaja võtta q selline, mille annab ebavõrdsus b q< a < b · (q + 1) было верным. Необходимо вычесть b · q из всех частей выражения. Тогда придем к неравенству такого вида: 0 < a − b · q < b . Meil on see, et avaldise a - b q väärtus on suurem kui null ja mitte suurem kui arvu b väärtus, sellest järeldub, et r \u003d a - b q. Saame, et arvu a saab esitada a \u003d b q + r. Nüüd on vaja kaaluda võimalust tähistada a \u003d b q + r b negatiivsete väärtuste korral. Numbri absoluutväärtus osutub positiivseks, siis saame a \u003d b q 1 + r, kus väärtus q 1 on mingi täisarv, r on täisarv, mis vastab tingimusele 0 ≤ r< b . Принимаем q = − q 1 , получим, что a = b · q + r для отрицательных b . Ainulaadsuse tõendamine Oletame, et a \u003d bq + r, q ja r on täisarvud, mille tegelik tingimus on 0 ≤ r< b , имеется еще одна форма записи в виде a = b · q 1 + r 1 , где q 1 ja r 1 on mõned numbrid, kus q 1 ≠ q , 0 ≤ r 1< b . Kui ebavõrdsus lahutatakse vasakult ja paremalt küljelt, saame 0 \u003d b · (q - q 1) + r - r 1, mis on samaväärne r - r 1 \u003d b · q 1 - q. Kuna kasutatakse moodulit, saame võrdsuse r - r 1 \u003d b q 1 - q. Antud tingimus ütleb, et 0 ≤ r< b и 0 ≤ r 1 < b запишется в виде r - r 1 < b . Имеем, что qja q 1- täisarvud ja q ≠ q 1, siis q 1 - q ≥ 1. Seega on meil b q 1 - q ≥ b. Sellest tulenev ebavõrdsus r - r 1< b и b · q 1 - q ≥ b указывают на то, что такое равенство в виде r - r 1 = b · q 1 - q невозможно в данном случае. Siit järeldub, et arvu a ei saa teisiti kujutada, välja arvatud sellise tähisega a \u003d b q + r. Kasutades võrdsust a \u003d b c + d, võite leida tundmatu dividendi a, kui teate jagajat b mittetäieliku jagatisega c ja ülejäänud d. Näide 1 Määrake dividend, kui jagunemisel saame - 21, mittetäielik jagatis 5 ja ülejäänud 12. Otsus
Tuleb arvutada dividend a teadaoleva jagajaga b \u003d - 21, mittetäielik jagatis c \u003d 5 ja ülejäänud d \u003d 12. Peame pöörduma võrdsuse a \u003d b c + d poole, millest saame a \u003d (- 21) 5 + 12. Vastavalt toimingute teostamise korrale korrutame - 21 5-ga, mille järel saame (- 21) 5 + 12 \u003d - 105 + 12 \u003d - 93. Vastus: - 93 . Jagaja ning mittetäieliku jagaja ja ülejäänud vahelist seost saab väljendada, kasutades võrdusi: b \u003d (a - d): c, c \u003d (a - d): b ja d \u003d a - b c. Nende abiga saame arvutada jagaja, osalise jagatuse ja ülejäänud. See taandub järjepidevuse leidmisele pärast täisarvu a jagamist b-ga tuntud dividendi, jagaja ja mittetäieliku jagatisega. Valem kehtib d \u003d a - b c. Vaatleme lahendust üksikasjalikult. Näide 2 Leidke ülejäänud arv, kui jagate täisarvu - 19 täisarvuga 3, mille teadaolev mittetäielik jagatis on võrdne - 7. Otsus
Jaotuse ülejäänud osa arvutamiseks kasutage valemit nagu d \u003d a - b · c. Tingimuste järgi on kõik andmed saadaval a \u003d - 19, b \u003d 3, c \u003d - 7. Seega saame d \u003d a - b c \u003d - 19 - 3 (- 7) \u003d - 19 - (- 21) \u003d - 19 + 21 \u003d 2 (erinevus on - 19 - (- 21). See näide arvutatakse lahutamise reegli järgi täisarvu negatiivne arv. Vastus: 2 . Kõik positiivsed täisarvud on loomulikud. Sellest järeldub, et jagamine toimub kõigi jagamisreeglite järgi, ülejäänud loomulike arvudega. Jagamise kiirus ülejäänud naturaalsete arvudega on oluline, sest mitte ainult positiivsete jagamine, vaid ka suvaliste täisarvude jagamise reeglid põhinevad sellel. Kõige mugavam jagamismeetod on veerg, kuna mittetäieliku või lihtsalt jagatise saamine jäägiga on lihtsam ja kiirem. Vaatleme lahendust üksikasjalikumalt. Näide 3 Jagage 14671 54-ga. Otsus
See jagamine tuleb teha veerus: See tähendab, et mittetäielik jagatis osutab 271 ja ülejäänud on 37. Vastus: 14 671: 54 \u003d 271. (peatus 37) Jaotamiseks positiivse arvu ülejäänud osaga negatiivse täisarvuga on vaja koostada reegel. 1. määratlus Mittetäielik jagatis positiivse täisarvu a jagamisel negatiivse täisarvuga b saame arvu, mis on vastuolus mittetäieliku jagatisega jagades arvude absoluutväärtused b-ga. Siis on ülejääk võrdne jäägiga, kui a jagatakse b-ga. Seega on see, et täisarvu positiivse arvu jagamise negatiivse täisarvuga mittetäielikku jagatist peetakse mittepositiivseks täisarvuks. Saame algoritmi: Vaatleme positiivse täisarvu jagamise negatiivse täisarvuga algoritmi näidet. Näide 4 Jagage ülejäänud 17-ga jagatuna - 5-ga. Otsus
Rakendame jagamise algoritmi positiivse täisarvu negatiivse täisarvuga. Peate jagama 17 - 5 mooduliga. Siit saame, et mittetäielik jagatis on 3 ja ülejäänud on 2. Vajaliku arvu saame jagades 17 jagamisega - 5 \u003d - 3 ülejäänud 2-ga. Vastus: 17: (- 5) \u003d - 3 (ülejäänud 2). Näide 5 Jagage 45 15-ga. Otsus
Numbrid peate jagama nende absoluutväärtusega Jagage arv 45 15-ga, saame jagatuse 3 ilma jäägita. See tähendab, et arv 45 jagub 15-ga ilma jäägita. Vastuses saame - 3, kuna jagamine viidi läbi modulo. 45: (- 15) = 45: - 15 = - 45: 15 = - 3 Vastus: 45: (− 15) = − 3 . Jagamisreegli sõnastus koos ülejäänud osaga on järgmine. Definitsioon 2 Negatiivse täisarvu a jagamisel positiivsega b mittetäieliku jagatise c saamiseks peate rakendama selle arvu vastandit ja lahutama sellest 1, seejärel arvutatakse ülejäänud d valemiga: d \u003d a - b · c. Reegli põhjal võime järeldada, et jagamisel saame mitte-negatiivse täisarvu. Lahuse täpsuse saamiseks kasutatakse algoritmi a jagamiseks b järgi b-ga: Vaatleme lahendi näidet, kus seda algoritmi rakendatakse. Näide 6 Leidke mittetäielik jagatis ja jagamise ülejäänud osa - 17 5-ga. Otsus
Jagage etteantud arvud modulo. Saame, et jagamisel jagatis on 3 ja ülejäänud on 2. Kuna saime 3, on vastupidine 3. Peate lahutama 1. − 3 − 1 = − 4 . Saame soovitud väärtuse, mis on võrdne - 4. Ülejäänud osa arvutamiseks vajate a \u003d - 17, b \u003d 5, c \u003d - 4, siis d \u003d a - b c \u003d - 17 - 5 (- 4) \u003d - 17 - (- 20) \u003d - 17 + 20 \u003d 3. See tähendab, et jagamise mittetäielik jagatis on arv - 4, ülejäänud on võrdne 3-ga. Vastus: (- 17): 5 \u003d - 4 (ülejäänud 3). Näide 7 Jagage negatiivne täisarv 1404 positiivse 26-ga. Otsus
On vaja jagada veeru ja mulli järgi. Saime arvude absoluutväärtuste jaotuse ilma jäägita. See tähendab, et jagamine toimub ilma jäägita ja soovitud jagatis \u003d - 54. Vastus: (− 1 404) : 26 = − 54 . On vaja sõnastada jagamisreegel ülejäänud negatiivsete täisarvudega. 3. definitsioon Mittetäieliku jagatise c saamiseks täisarvu negatiivse arvu a jagamisel täisarvu negatiivsega b on vaja läbi viia arvutused modulo, seejärel lisada 1, siis saame arvutada valemiga d \u003d a - b · c. Sellest järeldub, et negatiivsete täisarvude jagamise mittetäielik jagatis on positiivne arv. Koostame selle reegli algoritmi kujul: Vaatleme seda algoritmi näite abil. Näide 8 Leidke jagamisel mittetäielik jagatis ja jääk - 17 - 5. Otsus
Lahenduse õigsuse tagamiseks rakendame ülejäänud jaotusega jagamise algoritmi. Esiteks jagage arvud moodul. Siit saame, et mittetäielik jagatis \u003d 3 ja ülejäänud on 2. Reegli kohaselt on vaja lisada mittetäielik jagatis ja 1. Saame, et 3 + 1 \u003d 4. Sellest saame, et antud arvude jagamise mittetäielik jagatis on 4. Ülejäänud osa arvutamiseks kasutame valemit. Hüpoteesi kohaselt on meil a \u003d - 17, b \u003d - 5, c \u003d 4, siis saame valemi abil d \u003d a - b c \u003d - 17 - (- 5) 4 \u003d - 17 - (- 20) \u003d - 17 + 20 \u003d 3. Soovitud vastus, see tähendab, ülejäänud on 3 ja mittetäielik jagatis 4. Vastus: (- 17): (- 5) \u003d 4 (ülejäänud 3). Pärast ülejäänud numbrite jagamist peate kontrollima. See kontroll hõlmab kahte etappi. Kõigepealt kontrollitakse ülejäänud d mitteegatiivsust, olekut 0 ≤ d< b . При их выполнении разрешено выполнять 2 этап. Если 1 этап не выполнился, значит вычисления произведены с ошибками. Второй этап состоит из того, что равенство a = b · c + d должно быть верным. Иначе в вычисления имеется ошибка. Vaatame mõningaid näiteid. Näide 9 Jaotus tehti - 521 poolt - 12. Osakaal on 44, ülejäänud on 7. Kontrollima. Otsus
Kuna ülejäänu on positiivne arv, on selle väärtus väiksem kui jaguri moodul. Jagaja on - 12, mis tähendab, et selle moodul on 12. Võite minna järgmisse kontrollpunkti. Hüpoteesi kohaselt on meil a \u003d - 521, b \u003d - 12, c \u003d 44, d \u003d 7. Siit arvutame b c + d, kus b c + d \u003d - 12 44 + 7 \u003d - 528 + 7 \u003d - 521. Siit järeldub, et võrdsus on tõsi. Kontrollimine õnnestus. Näide 10 Tehke jaotuskontroll (- 17): 5 \u003d - 3 (ülejäänud - 2). Kas võrdsus on tõsi? Otsus
Esimese etapi mõte on see, et on vaja kontrollida ülejäänud arvude jagunemist. Seega on selge, et toiming tehti valesti, kuna ülejäänud osa on võrdne - 2. Ülejäänud osa ei ole negatiivne. Meil on teine \u200b\u200btingimus täidetud, kuid antud juhul ebapiisav. Vastus: mitte. Näide 11 Arv - 19 jagatud - 3-ga. Mittetäielik jagatis on 7 ja ülejäänud on 1. Kontrollige, kas arvutus on õige. Otsus
Ülejäänud 1 antakse. Ta on positiivne. See on väiksem kui jagaja moodul, mis tähendab, et esimene etapp viiakse läbi. Liigume teisele etapile. Arvutame avaldise b c + d väärtuse. Hüpoteesi kohaselt on meil b \u003d - 3, c \u003d 7, d \u003d 1, seega, asendades arvväärtused, saame b c + d \u003d - 3 7 + 1 \u003d - 21 + 1 \u003d - 20. Sellest järeldub, et a \u003d b c + d võrdsus ei kehti, kuna tingimus annab a \u003d - 19. Sellest järeldub, et jagamine tehti veaga. Vastus: mitte. Kui märkate tekstis viga, valige see ja vajutage klahvikombinatsiooni Ctrl + Enter Vaatame lihtsat näidet: Mõnikord ei saa looduslikku arvu täielikult jagada. Mõelge näiteks ülesandele: Otsus: Me teame, et 16 5-ga ei ole jagatav. Lähim väiksem arv, mis jaguneb 5-ga, on 15 ja 1 ülejäänud. Numbri 15 võime kirjutada 5⋅3. Selle tulemusena (16 - dividend, 5 - jagaja, 3 - mittetäielik jagatis, 1 - ülejäänud). Sain valem jagamine ülejäänudmille abil saate teha otsuse kontrollimine. a=
b⋅
c+
d Vastus: iga laps võtab 3 mänguasja ja üks mänguasi jääb alles. Ülejäänud osa peab alati olema väiksem kui jagaja. Kui ülejääk on jagamise ajal , tähendab see, et dividend tuleb jagada täielikult või ülejäänu jaguri kohta puudub. Kui jagamisel on ülejääk suurem kui jagaja, tähendab see, et leitud arv pole kõige suurem. On suurem arv, mis jagab dividendi ja ülejäänu on väiksem kui jagaja. Küsimused teemal "Ülejäänud jagunemine":
Kas ülejäänud osa võib olla võrdne jagajaga? Kuidas leida dividend mittetäieliku jagaja, jagaja ja ülejäänud järgi? Näide 1:
Otsus: 258 - dividend, b) Jagame veeruga: 1873 - dividend, Asendame valemis ja kontrollime, kas lahendasime näite õigesti: Näide 2:
Vastus: Näide 3:
Vastus: Näide 4:
Otsus: b) Lahendame valemi abil: Ülesanne:
Traat 4m. tuleb lõigata tükkideks 13cm. Kui palju neid tükke saate? Otsus: Vastus: välja tuleb 30 tükki ja traati jääb 10 cm.![]() ja arvu mooduli omaduste tõttu võrdsus
ja arvu mooduli omaduste tõttu võrdsus ![]() .
.
![]() ... Saadud ebavõrdsustest ja
... Saadud ebavõrdsustest ja ![]() sellest järeldub, et vormi võrdsus
sellest järeldub, et vormi võrdsus ![]() meie eeldusel võimatu. Seetõttu pole numbri a muud esindust, välja arvatud a \u003d b q + r.
meie eeldusel võimatu. Seetõttu pole numbri a muud esindust, välja arvatud a \u003d b q + r.Seosed dividendi, jagaja, mittetäieliku jagaja ja ülejäänud vahel
Jagamine ülejäänud positiivsete täisarvudega, näited

Jagamisreegel positiivse täisarvu ülejäänud osaga negatiivse täisarvuga, näited
Jagamine negatiivse täisarvu ülejäänud osaga positiivse täisarvuga, näited

Jagamisreegel koos ülejäänud negatiivsete täisarvudega, näited
Täisarvude jagamise tulemuse kontrollimine ülejäänuga
Mõned jagatavuse kriteeriumid üsna lihtne, mõni raskem. Sellelt lehelt leiate nii algarvude jagamiskriteeriumid, nagu näiteks 2, 3, 5, 7, 11, kui ka liitarvude, näiteks 6 või 12, jagamiskriteeriumid.
Loodan, et see teave on teile kasulik.
Head õppimist! Jagatavus 2-ga
Teisisõnu, kui numbri viimane number on 2
, 4
, 6
, 8
või 0
- arv jagub 2-ga, kui mitte, siis see ei ole jagatav
Näiteks numbrid: 23 4
, 8270
, 1276
, 9038
, 502
jagunevad 2-ga, kuna on ühtlased.
Ja numbrid: 23 5
, 137
, 2303
ei ole jagatavad 2-ga, kuna on paarimatud. Jagatavus 3-ga
Niisiis, selleks, et aru saada, kas number jagub 3-ga, tuleb lihtsalt kokku liita numbrid, millest see koosneb.
See näeb välja selline: 3987 ja 141 jaguvad 3-ga, sest esimesel juhul 3 + 9 + 8 + 7 \u003d 27
(27: 3 \u003d 9 - jagatav 3-ga ilma ostakita) ja teises 1 + 4 + 1 \u003d 6
(6: 3 \u003d 2 - jagub 3-ga ka ilma ostakita).
Kuid arvud: 235 ja 566 ei ole jagatavad 3-ga, sest 2 + 3 + 5 \u003d 10
ja 5 + 6 + 6 \u003d 17
(ja me teame, et ei 10 ega 17 ei jagu 3-ga ilma jäägita). Jagatavus 4-ga
Näiteks: 1 00
ja 3 64
jagatakse 4-ga, sest esimesel juhul lõpeb number 00
ja teises edasi 64
, mis omakorda jagub 4-ga ilma jäägita (64: 4 \u003d 16)
Numbrid 3 57
ja 8 86
ei ole jagatavad 4-ga, sest kumbagi 57
ega ka 86
ei ole jagatavad 4-ga, mis tähendab, et need ei vasta antud jagatavuse kriteeriumile. Jagatavus 5-ga
See tähendab, et kõik numbrid, mis lõpevad numbritega 0
ja 5
nt 1235 5
ja 43 0
, jäävad reegli alla ja jaguvad 5-ga.
Ja näiteks 1549 3
ja 56 4
ei lõppe arvuga 5 ega 0, mis tähendab, et neid ei saa ilma jäägita jagada 5-ga. Jagatavus 6-ga
Numbrid 138 ja 474 on paarisarvud ja vastavad jagatavuse kriteeriumidele 3-ga (1 + 3 + 8 \u003d 12, 12: 3 \u003d 4 ja 4 + 7 + 4 \u003d 15, 15: 3 \u003d 5), mis tähendab, et need on jagatavad 6-ga. Kuid 123 ja 447, ehkki need on jagatavad 3-ga (1 + 2 + 3 \u003d 6, 6: 3 \u003d 2 ja 4 + 4 + 7 \u003d 15, 15: 3 \u003d 5), kuid need on paarimatud, mis tähendab, et need ei vasta jagamiskriteeriumile 2, ja seetõttu ei vasta jagatavuse kriteerium 6-ga. Jagatavus 7-ga
Kõlab üsna segaselt, kuid praktikas on see lihtne. Vaadake ise: number 95
9 jagub 7-ga, sest 95
-2 * 9 \u003d 95-18 \u003d 77, 77: 7 \u003d 11 (77 jagub 7-ga ilma jäägita). Veelgi enam, kui teisenduste käigus saadud arvuga tekkis raskusi (selle suuruse tõttu on raske mõista, kas see jagub 7-ga või mitte, siis saab seda protseduuri jätkata nii mitu korda, kui peate vajalikuks).
Näiteks, 45
5 ja 4580
1 on märke jagatavusest 7. Esimesel juhul on kõik üsna lihtne: 45
-2 * 5 \u003d 45-10 \u003d 35, 35: 7 \u003d 5. Teisel juhul teeme seda: 4580
-2 * 1 \u003d 4580-2 \u003d 4578. Meil on raske aru saada, kas 457
8 korda 7, nii et korrake protsessi: 457
-2 * 8 \u003d 457-16 \u003d 441. Ja jälle kasutame jagamiskriteeriumi, kuna meil on endiselt kolmekohaline number 44
1. Niisiis, 44
-2 * 1 \u003d 44-2 \u003d 42, 42: 7 \u003d 6, st. 42 jagub 7-ga ilma jäägita, mis tähendab, et 45801 jagub 7-ga.
Aga numbrid 11
1 ja 34
5 ei ole jagatav 7-ga, kuna 11
-2 * 1 \u003d 11 - 2 \u003d 9 (9 ei ole 7-ga ühtlaselt jagatav) ja 34
-2 * 5 \u003d 34-10 \u003d 24 (24 ei jaga 7-ga ühtlaselt). Jagatavus 8-ga
Numbrid 1 000
või 1 088
jagub 8-ga: esimene lõpeb 000
, teine 88
: 8 \u003d 11 (jagub 8-ga ilma jäägita).
Kuid numbrid 1 100
või 4 757
ei ole 8-ga jagatavad, kuna arvud 100
ja 757
ei jaga 8-ga ühtlaselt. Jagatav 9-ga
Näiteks: 3987 ja 144 jaguvad 9-ga, sest esimesel juhul 3 + 9 + 8 + 7 \u003d 27
(27: 9 \u003d 3 - jagub 9-ga ilma ostakita) ja teises 1 + 4 + 4 \u003d 9
(9: 9 \u003d 1 - jagub ka 9-ga ilma ostakita).
Kuid arvud: 235 ja 141 ei ole jagatavad 9-ga, sest 2 + 3 + 5 \u003d 10
ja 1 + 4 + 1 \u003d 6
(ja me teame, et ei 10 ega 6 pole jagamata 9-ga jagatavad). Jagatavus 10, 100, 1000 ja muude bittiühikutega
Teisisõnu on meil näiteks sellised arvud: 654 0
, 46400
, 867000
, 6450
... millest kõik jagunevad 1-ga 0
; 46400
ja 867 000
jagatakse ka 1-ga 00
; ja ainult üks neist - 867 000
jagub 1-ga 000
.
Numbreid, mille lõpus on vähem nulle kui bitiühikul, ei saa selle bitiühikuga jagada, näiteks 600 30
ja 7 93
pole jagatav 1 00
.Jagatav 11-ga
Selle selgemaks muutmiseks soovitan kaaluda näiteid: 2
35
4 jagub 11-ga, kuna ( 2
+5
)-(3+4)=7-7=0. 29
19
4 jagub ka 11-ga, kuna ( 9
+9
)-(2+1+4)=18-7=11.
Kuid 1 1
1 või 4
35
4 ei ole jagatav 11-ga, kuna esimesel juhul saame (1 + 1) - 1
\u003d 1 ja teises ( 4
+5
)-(3+4)=9-7=2.Jagatav 12-ga
Näiteks 300 ja 636 vastavad jagatavuse märkidele 4-ga (kaks viimast numbrit on nullid või jaguvad 4-ga) ja jagamismärkidega 3-ga (numbrite ja esimese ning kolmekordse arvu summa jagub 3-ga) ja znit jagavad neid 12-ga ilma jäägita.
Kuid 200 või 630 ei ole jagatavad 12-ga, sest esimesel juhul vastab number ainult jagatavuse kriteeriumile 4 ja teisel - ainult jagamiskriteeriumile 3, kuid mitte üheaegselt mõlemale märgile. Jagatavus 13-ga
Võtame näiteks 70
2. Niisiis 70
+ 4 * 2 \u003d 78, 78: 13 \u003d 6 (78 jagub 13-ga ilma jäägita), mis tähendab 70
2 on jagatav 13-ga ilma jäägita. Teine näide on number 114
4. 114
+ 4 * 4 \u003d 130, 130: 13 \u003d 10. Arv 130 jagub 13-ga ilma jäägita, mis tähendab, et määratud arv vastab jagamiskriteeriumile 13-ga.
Kui võtame numbrid 12
5 või 21
2, siis saame 12
+ 4 * 5 \u003d 32 ja 21
+ 4 * 2 \u003d 29 ja 32 ega 29 ei jagu 13-ga ilma jäägita, mis tähendab, et etteantud arvud ei jaga 13-ga ühtlaselt.Numbrite jagatavus
Järelejäänud täisarvude jaotuse mõistmine
Ülejäänud täisarvude jagatavuse teoreem
Seos dividendi, jagaja, mittetäieliku jagaja ja ülejäänud vahel
Jagamisreegel positiivse täisarvu ülejäänud osaga negatiivse täisarvuga, näited

Jagamisreegel koos ülejäänud negatiivsete täisarvudega, näited
Täisarvude jagamise tulemuse kontrollimine ülejäänuga
15:5=3
Selles näites jagatakse looduslik arv 15 täielikult3-ks, ülejäänud pole.
Kapis oli 16 mänguasja. Rühmas oli viis last. Iga laps võttis sama palju mänguasju. Mitu mänguasja on igal lapsel?
Jagage arv 16 veeruga 5-ga ja saate:
a - dividend,
b - jagaja,
c - mittetäielik jagatis,
d Kas ülejäänud osa.Jaotuse ülejäänud osa
Kas ülejäänud osa võib olla suurem kui jagaja?
Vastus on eitav.
Vastus on eitav.
Vastus: mittetäieliku jagaja, jagaja ja ülejäänud väärtused asendatakse valemiga ja leiame dividendi. Valem:
a \u003d b⋅c + d
Tehke jagamine ülejäänuga ja kontrollige: a) 258: 7 b) 1873: 8
a) Jagame veeruga: 
7 - jagaja,
36 - mittetäielik jagatis,
6 on ülejäänud. Ülejäänud vähem kui jagaja 6<7.
7⋅36+6=252+6=258
8 - jagaja,
234 - mittetäielik jagatis,
1 on ülejäänud osa. Ülejäänud vähem kui jagaja 1<8.
8⋅234+1=1872+1=1873
Mis on looduslike arvude jagamisel saadud jäägid: a) 3 b) 8?
a) Ülejäänud on väiksem kui jagaja, seega väiksem kui 3. Meie juhul võib jääk olla 0, 1 või 2.
b) Ülejäänud on väiksem kui jagaja, seega väiksem kui 8. Meie juhul võib jääk olla 0, 1, 2, 3, 4, 5, 6 või 7.
Mis on suurim jääk, mida on võimalik saada loodusarvude jagamisel: a) 9 b) 15?
a) Ülejäänud on väiksem kui jagaja, seega väiksem kui 9. Kuid peame märkima suurima jäägi. See on jagajale lähim arv. See arv on 8.
b) Ülejääk on väiksem kui jagaja, seega väiksem kui 15. Kuid peame märkima suurima jäägi. See on jagajale lähim arv. See arv on 14.
Leidke dividend: a) a: 6 \u003d 3 (ülejäänud 4) b) c: 24 \u003d 4 (ülejäänud 11)
a) Lahendame järgmise valemi abil:
a \u003d b⋅c + d
(a - dividend, b - jagaja, c - osaline jagatis, d - ülejäänud.)
a: 6 \u003d 3 (ülejäänud 4)
(a - dividend, 6 - jagaja, 3 - mittetäielik jagatis, 4 - ülejääk.) Asendage arvud valemis:
a \u003d 6⋅3 + 4 \u003d 22
Vastus: a \u003d 22
a \u003d b⋅c + d
(a - dividend, b - jagaja, c - osaline jagatis, d - ülejäänud.)
alates: 24 \u003d 4 (ülejäänud 11)
(c - dividend, 24 - jagaja, 4 - mittetäielik jagatis, 11 - ülejäänud.) Asendage arvud valemis:
c \u003d 24-4 + 11 \u003d 107
Vastus: c \u003d 107
Esiteks peate teisendama meetrit sentimeetriteks.
4m \u003d 400cm.
Võite jagada selle veeru järgi või saame oma meelest:
400: 13 \u003d 30 (ülejäänud 10)
Kontrollime:
13⋅30+10=390+10=400