Eckseite 2 3 Sockelhöhe. Dreieckshöhe

Bei der Lösung geometrischer Probleme ist es sinnvoll, diesem Algorithmus zu folgen. Beim Lesen der Aufgabenstellung ist es notwendig

Fertige eine Zeichnung an. Die Zeichnung sollte dem Zustand des Problems so gut wie möglich entsprechen, daher besteht ihre Hauptaufgabe darin, bei der Lösungsfindung zu helfen
Wenden Sie alle Daten aus der Aufgabenbedingung auf die Zeichnung an
Schreiben Sie alle geometrischen Konzepte auf, die in der Aufgabe vorkommen
Erinnern Sie sich an alle Theoreme, die sich auf dieses Konzept beziehen
Tragen Sie in der Zeichnung alle Beziehungen zwischen den Elementen einer geometrischen Figur ein, die sich aus diesen Sätzen ergeben

Wenn die Aufgabe beispielsweise die Wörter Winkelhalbierende eines Dreiecks enthält, müssen Sie sich die Definition und Eigenschaften der Winkelhalbierenden merken und in der Zeichnung gleiche oder proportionale Segmente und Winkel bezeichnen.

In diesem Artikel finden Sie die grundlegenden Eigenschaften eines Dreiecks, die Sie kennen müssen, um Probleme erfolgreich zu lösen.

DREIECK.

Fläche eines Dreiecks.

1. ,

hier - eine beliebige Seite des Dreiecks, - die zu dieser Seite abgesenkte Höhe.

2. ,

hier und sind beliebige Seiten des Dreiecks, ist der Winkel zwischen diesen Seiten:

3. Reiherformel:

Hier - die Längen der Seiten des Dreiecks, - der Halbumfang des Dreiecks,

4. ,

hier - der Halbumfang des Dreiecks, - der Radius des eingeschriebenen Kreises.

Seien die Längen der Tangentensegmente.

Dann kann Herons Formel in der folgenden Form geschrieben werden:

6. ,

hier - die Längen der Seiten des Dreiecks, - der Radius des umschriebenen Kreises.

Nimmt man einen Punkt auf einer Seite eines Dreiecks, der diese Seite im Verhältnis m:n teilt, dann teilt die Strecke, die diesen Punkt mit dem Scheitelpunkt des entgegengesetzten Winkels verbindet, das Dreieck in zwei Dreiecke, deren Flächen als m bezeichnet werden :N:

Das Verhältnis der Flächen ähnlicher Dreiecke ist gleich dem Quadrat des Ähnlichkeitskoeffizienten.

Dreieck-Median

Dies ist ein Liniensegment, das den Scheitelpunkt des Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet.

Dreiecksmediane schneiden sich in einem Punkt und teilen sich den Schnittpunkt im Verhältnis 2:1, von oben gezählt.

Der Schnittpunkt der Mediane eines regelmäßigen Dreiecks teilt den Median in zwei Segmente, von denen das kleinere gleich dem Radius des eingeschriebenen Kreises und das größere gleich dem Radius des umschriebenen Kreises ist.

Der Radius des umschriebenen Kreises ist doppelt so groß wie der Radius des eingeschriebenen Kreises: R=2r

Mittlere Länge beliebiges Dreieck

hier - der zur Seite gezogene Median - die Längen der Seiten des Dreiecks.

Winkelhalbierende eines Dreiecks

Dies ist ein Segment der Winkelhalbierenden eines beliebigen Winkels eines Dreiecks, das den Scheitelpunkt dieses Winkels mit der gegenüberliegenden Seite verbindet.

Winkelhalbierende eines Dreiecks teilt die Seite in Segmente proportional zu den angrenzenden Seiten:

Dreieckshalbierende schneiden sich in einem Punkt, dem Mittelpunkt des eingeschriebenen Kreises.

Alle Punkte auf der Winkelhalbierenden haben von den Seiten des Winkels den gleichen Abstand.

Dreieckshöhe

Dies ist ein Abschnitt der Senkrechten, der vom Scheitelpunkt des Dreiecks nach unten abgesenkt wird gegenüberliegende Seite, oder seine Fortsetzung. In einem stumpfen Dreieck liegt die vom Scheitelpunkt eines spitzen Winkels ausgehende Höhe außerhalb des Dreiecks.

Die Höhen eines Dreiecks schneiden sich in einem Punkt, der aufgerufen wird das Orthozentrum des Dreiecks.

Um die Höhe eines Dreiecks zu ermitteln Zur Seite gezogen, müssen Sie seine Fläche auf jede mögliche Weise ermitteln und dann die Formel verwenden:

Mittelpunkt eines um ein Dreieck umschriebenen Kreises, liegt im Schnittpunkt der zu den Seiten des Dreiecks gezogenen Mittelsenkrechten.

Der Radius des umschriebenen Kreises eines Dreiecks kann mit folgenden Formeln ermittelt werden:

Hier sind die Längen der Seiten des Dreiecks: Fläche eines Dreiecks.

wobei die Seitenlänge des Dreiecks der entgegengesetzte Winkel ist. (Diese Formel folgt aus dem Sinussatz).

Dreiecksungleichung

Jede Seite des Dreiecks ist kleiner als die Summe und größer als die Differenz der beiden anderen.

Die Summe der Längen zweier beliebiger Seiten ist immer größer als die Länge der dritten Seite:

Der größeren Seite gegenüber liegt ein größerer Winkel; gegenüber dem größeren Winkel liegt die größere Seite:

Wenn, dann umgekehrt.

Sinussatz:

Die Seiten eines Dreiecks sind proportional zu den Sinuswerten der entgegengesetzten Winkel:

Kosinussatz:

Das Quadrat einer Seite eines Dreiecks ist gleich der Summe der Quadrate der beiden anderen Seiten, ohne das Produkt dieser Seiten durch den Kosinus des Winkels zwischen ihnen zu verdoppeln:

Rechtwinkliges Dreieck

- Es ist ein Dreieck, bei dem einer der Winkel 90° beträgt.

Summe scharfe Kanten rechtwinkliges Dreieck entspricht 90°.

Die Hypotenuse ist die Seite, die dem 90°-Winkel gegenüberliegt. Die Hypotenuse ist die längste Seite.

Satz des Pythagoras:

Das Quadrat der Hypotenuse ist gleich der Summe der Quadrate der Beine:

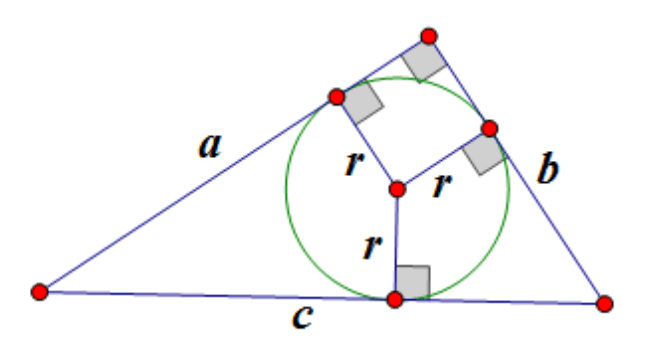
Der Radius eines in ein rechtwinkliges Dreieck eingeschriebenen Kreises beträgt

hier - der Radius des eingeschriebenen Kreises, - die Beine, - die Hypotenuse:

Mittelpunkt eines um ein rechtwinkliges Dreieck umschriebenen Kreises liegt in der Mitte der Hypotenuse:

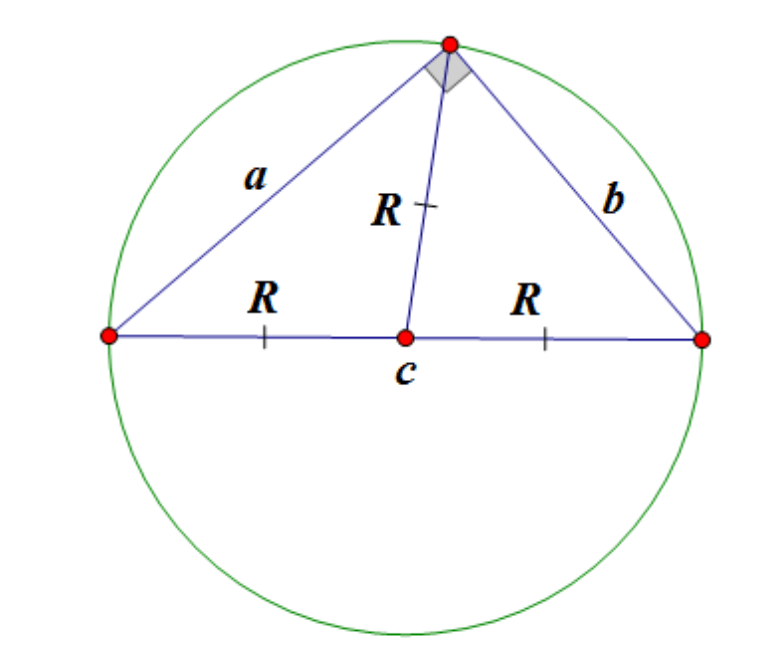
Median eines rechtwinkligen Dreiecks, das zur Hypotenuse gezogen wird gleich der Hälfte der Hypotenuse.

Definition von Sinus, Cosinus, Tangens und Kotangens eines rechtwinkligen Dreiecks sehen

Das Verhältnis der Elemente in einem rechtwinkligen Dreieck:

Das Quadrat der Höhe eines rechtwinkligen Dreiecks, das von einem Scheitelpunkt aus gezeichnet wird rechter Winkel, ist gleich dem Produkt der Projektionen der Beine auf die Hypotenuse:

Das Quadrat des Beins ist gleich dem Produkt aus Hypotenuse und der Projektion des Beins auf die Hypotenuse:

Bein liegt an der Ecke gleich der halben Hypotenuse:

Gleichschenkligen Dreiecks.

Halbierende gleichschenkligen Dreiecks Zur Basis gezeichnet ist der Median und die Höhe.

In einem gleichschenkligen Dreieck sind die Winkel an der Basis gleich.

Oberer Winkel.

Ich - Seiten

Und - Winkel an der Basis.

Höhe, Winkelhalbierende und Median.

Aufmerksamkeit! Die Höhe, die Winkelhalbierende und der zur lateralen Seite gezeichnete Median stimmen nicht überein.

rechtwinkliges Dreieck

(oder gleichseitiges Dreieck ) ist ein Dreieck, dessen Seiten und Winkel einander gleich sind.

Fläche eines gleichseitigen Dreiecks ist gleich

Wo ist die Seitenlänge des Dreiecks?

Mittelpunkt eines Kreises, der in ein gleichseitiges Dreieck eingeschrieben ist, fällt mit dem Mittelpunkt des um ein gleichseitiges Dreieck umschriebenen Kreises zusammen und liegt im Schnittpunkt der Mediane.

Schnittpunkt der Mediane eines gleichseitigen Dreiecks teilt den Median in zwei Segmente, von denen das kleinere gleich dem Radius des eingeschriebenen Kreises und das größere gleich dem Radius des umschriebenen Kreises ist.

Wenn einer der Winkel eines gleichschenkligen Dreiecks 60° beträgt, dann ist das Dreieck regelmäßig.

Mittellinie des Dreiecks

Dies ist ein Segment, das die Mittelpunkte zweier Seiten verbindet.

In der Abbildung ist DE die Mittellinie des Dreiecks ABC.

Die Mittellinie des Dreiecks verläuft parallel zur dritten Seite und entspricht der Hälfte davon: DE||AC, AC=2DE

Äußere Ecke eines Dreiecks

Dies ist der Winkel, der an einen beliebigen Winkel des Dreiecks angrenzt.

Ein Außenwinkel eines Dreiecks ist gleich der Summe zweier Winkel, die nicht an ihn angrenzend sind.

Trigonometrische Funktionen eines Außenwinkels:

Zeichen der Gleichheit von Dreiecken:

1 . Wenn zwei Seiten und der Winkel zwischen ihnen eines Dreiecks jeweils gleich zwei Seiten und der Winkel zwischen ihnen eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent.

2 . Wenn eine Seite und zwei benachbarte Winkel eines Dreiecks jeweils gleich einer Seite und zwei benachbarten Winkeln eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent.

3 Wenn drei Seiten eines Dreiecks jeweils gleich drei Seiten eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent.

Wichtig: da in einem rechtwinkligen Dreieck offensichtlich zwei Winkel gleich sind, dann für Gleichheit zweier rechtwinkliger Dreiecke Es müssen nur zwei Elemente gleich sein: zwei Seiten oder eine Seite und ein spitzer Winkel.

Ähnlichkeitszeichen von Dreiecken:

1 . Wenn zwei Seiten eines Dreiecks proportional zu zwei Seiten eines anderen Dreiecks sind und die zwischen diesen Seiten eingeschlossenen Winkel gleich sind, dann sind diese Dreiecke ähnlich.

2 . Wenn drei Seiten eines Dreiecks proportional zu drei Seiten eines anderen Dreiecks sind, dann sind diese Dreiecke ähnlich.

3 . Wenn zwei Winkel eines Dreiecks gleich zwei Winkeln eines anderen Dreiecks sind, dann sind diese Dreiecke ähnlich.

Wichtig: In ähnlichen Dreiecken liegen ähnliche Seiten gleichen Winkeln gegenüber.

Satz von Menelaos

Die Gerade schneidet das Dreieck, wobei ihr Schnittpunkt mit der Seite, ihr Schnittpunkt mit der Seite und ihr Schnittpunkt mit der Verlängerung der Seite ist. Dann

Ihre Privatsphäre ist uns wichtig. Aus diesem Grund haben wir eine Datenschutzrichtlinie entwickelt, die beschreibt, wie wir Ihre Daten verwenden und speichern. Bitte lesen Sie unsere Datenschutzbestimmungen und teilen Sie uns mit, wenn Sie Fragen haben.

Erhebung und Nutzung personenbezogener Daten

Unter personenbezogenen Daten versteht man Daten, die dazu genutzt werden können, eine bestimmte Person zu identifizieren oder mit ihr in Kontakt zu treten.

Sie können jederzeit um die Angabe Ihrer persönlichen Daten gebeten werden, wenn Sie mit uns Kontakt aufnehmen.

Im Folgenden finden Sie einige Beispiele für die Arten personenbezogener Daten, die wir möglicherweise sammeln, und wie wir diese Informationen verwenden können.

Welche persönlichen Daten wir sammeln:

Wenn Sie auf der Website eine Bewerbung einreichen, erfassen wir möglicherweise verschiedene Informationen, einschließlich Ihres Namens, Ihrer Telefonnummer, Ihrer E-Mail-Adresse usw.

Wie wir Ihre persönlichen Daten verwenden:

Von uns gesammelt Persönliche Angaben ermöglicht es uns, Sie zu kontaktieren und Sie über einzigartige Angebote, Werbeaktionen und andere Veranstaltungen sowie bevorstehende Veranstaltungen zu informieren.
Von Zeit zu Zeit verwenden wir Ihre persönlichen Daten möglicherweise, um Ihnen wichtige Mitteilungen und Nachrichten zu senden.
Wir können personenbezogene Daten auch für interne Zwecke verwenden, beispielsweise zur Durchführung von Audits, Datenanalysen und verschiedenen Forschungsarbeiten, um die von uns bereitgestellten Dienste zu verbessern und Ihnen Empfehlungen zu unseren Diensten zu geben.
Wenn Sie an einer Verlosung, einem Wettbewerb oder einem ähnlichen Anreiz teilnehmen, können wir die von Ihnen bereitgestellten Informationen zur Verwaltung solcher Programme verwenden.

Weitergabe an Dritte

Wir geben die von Ihnen erhaltenen Informationen nicht an Dritte weiter.

Ausnahmen:

Bei Bedarf – in Übereinstimmung mit dem Gesetz, einer gerichtlichen Anordnung, in Gerichtsverfahren und/oder aufgrund öffentlicher Anfragen oder Anfragen von Regierungsbehörden auf dem Territorium der Russischen Föderation - Ihre persönlichen Daten offenlegen. Wir können auch Informationen über Sie offenlegen, wenn wir zu dem Schluss kommen, dass eine solche Offenlegung aus Sicherheits-, Strafverfolgungs- oder anderen Gründen des öffentlichen Interesses notwendig oder angemessen ist.
Im Falle einer Umstrukturierung, Fusion oder eines Verkaufs können wir die von uns erfassten personenbezogenen Daten an den jeweiligen Rechtsnachfolger weitergeben.

Schutz personenbezogener Daten

Wir treffen Vorkehrungen – einschließlich administrativer, technischer und physischer –, um Ihre persönlichen Daten vor Verlust, Diebstahl und Missbrauch sowie vor unbefugtem Zugriff, Offenlegung, Änderung und Zerstörung zu schützen.

Wahrung Ihrer Privatsphäre auf Unternehmensebene

Um sicherzustellen, dass Ihre persönlichen Daten sicher sind, informieren wir unsere Mitarbeiter über Datenschutz- und Sicherheitspraktiken und setzen die Datenschutzpraktiken strikt durch.

E A → ⋅ B C → + E B → ⋅ C A → + E C → ⋅ A B → = 0 (\displaystyle (\overrightarrow (EA))\cdot (\overrightarrow (BC))+(\overrightarrow (EB))\cdot (\ overrightarrow (CA))+(\overrightarrow (EC))\cdot (\overrightarrow (AB))=0)

(Um die Identität zu beweisen, sollte man die Formeln verwenden

A B → = E B → − E A → , B C → = E C → − E B → , C A → = E A → − E C → (\displaystyle (\overrightarrow (AB))=(\overrightarrow (EB))-(\overrightarrow (EA )),\,(\overrightarrow (BC))=(\overrightarrow (EC))-(\overrightarrow (EB)),\,(\overrightarrow (CA))=(\overrightarrow (EA))-(\overrightarrow (EG)))

Der Punkt E sollte als Schnittpunkt der beiden Höhen des Dreiecks angenommen werden.)

Orthozentrum isogonal konjugiert zum Zentrum umschriebener Kreis .
Orthozentrum liegt auf der gleichen Linie wie der Schwerpunkt, der Mittelpunkt umschriebener Kreis und der Mittelpunkt des Kreises aus neun Punkten (siehe die Euler-Linie).
Orthozentrum Ein spitzes Dreieck ist der Mittelpunkt eines Kreises, der in sein Orthodreieck eingeschrieben ist.
Der Mittelpunkt eines Dreiecks, das durch das Orthozentrum beschrieben wird, mit Eckpunkten an den Mittelpunkten der Seiten des gegebenen Dreiecks. Das letzte Dreieck wird in Bezug auf das erste Dreieck als zusätzliches Dreieck bezeichnet.
Die letzte Eigenschaft lässt sich wie folgt formulieren: Der Mittelpunkt eines um ein Dreieck umschriebenen Kreises dient Orthozentrum zusätzliches Dreieck.
Punkte, symmetrisch Orthozentrum Das Dreieck liegt mit seinen Seiten auf dem umschriebenen Kreis.
Punkte, symmetrisch Orthozentrum Dreiecke in Bezug auf die Mittelpunkte der Seiten liegen ebenfalls auf dem umschriebenen Kreis und fallen mit Punkten zusammen, die den entsprechenden Eckpunkten diametral gegenüber liegen.
Wenn UM ist dann der Mittelpunkt des umschriebenen Kreises ΔABC O H → = O A → + O B → + O C → (\displaystyle (\overrightarrow (OH))=(\overrightarrow (OA))+(\overrightarrow (OB))+(\overrightarrow (OC))) ,
Der Abstand vom Scheitelpunkt des Dreiecks zum Orthozentrum ist doppelt so groß wie der Abstand vom Mittelpunkt des umschriebenen Kreises zur gegenüberliegenden Seite.
Jedes Segment, aus dem gezogen wird Orthozentrum halbiert immer den Eulerkreis, bis er den umschriebenen Kreis schneidet. Orthozentrum ist das Zentrum der Homothetie dieser beiden Kreise.
Satz von Hamilton. Drei Liniensegmente, die das Orthozentrum mit den Eckpunkten eines spitzwinkligen Dreiecks verbinden, teilen es in drei Dreiecke mit demselben Eulerkreis (Kreis aus neun Punkten) wie das ursprüngliche spitzwinklige Dreieck.
Konsequenzen des Satzes von Hamilton:
- Drei Liniensegmente, die das Orthozentrum mit den Eckpunkten eines spitzwinkligen Dreiecks verbinden, teilen es in drei Teile Hamilton-Dreieck mit gleichen Radien umschriebener Kreise.
- Die Radien der umschriebenen Kreise der drei Hamilton-Dreiecke sind gleich dem Radius des Kreises, der das ursprüngliche spitzwinklige Dreieck umschreibt.
In einem spitzen Dreieck liegt das Orthozentrum innerhalb des Dreiecks; stumpf - außerhalb des Dreiecks; in einem rechteckigen - am Scheitelpunkt eines rechten Winkels.

Höheneigenschaften eines gleichschenkligen Dreiecks

Wenn in einem Dreieck zwei Höhen gleich sind, dann ist das Dreieck gleichschenklig (Satz von Steiner-Lemus) und die dritte Höhe ist sowohl der Median als auch die Winkelhalbierende des Winkels, aus dem es hervorgeht.
Das Umgekehrte gilt auch: In einem gleichschenkligen Dreieck sind zwei Höhen gleich und die dritte Höhe ist sowohl Mittelwert als auch Winkelhalbierende.
Bei einem gleichseitigen Dreieck sind alle drei Höhen gleich.

Eigenschaften der Basen der Höhen eines Dreiecks

Stiftungen Höhen bilden das sogenannte Orthodreieck, das seine eigenen Eigenschaften hat.
Der in der Nähe des Orthodreiecks beschriebene Kreis ist der Euler-Kreis. Auf diesem Kreis liegen auch drei Mittelpunkte der Seiten des Dreiecks und drei Mittelpunkte der drei Segmente, die das Orthozentrum mit den Eckpunkten des Dreiecks verbinden.
Eine weitere Formulierung der letzten Eigenschaft:
- Satz von Euler für einen Kreis aus neun Punkten. Stiftungen drei Höhen beliebiges Dreieck, die Mittelpunkte seiner drei Seiten ( Grundlagen seines Inneren Mediane) und die Mittelpunkte der drei Segmente, die seine Eckpunkte mit dem Orthozentrum verbinden, liegen alle auf demselben Kreis (auf Neun-Punkte-Kreis).
Satz. In jedem Dreieck ist das Verbindungsliniensegment Gründe zwei Höhen Dreieck schneidet ein Dreieck ab, das dem angegebenen ähnlich ist.
Satz. In einem Dreieck das Verbindungsliniensegment Gründe zwei Höhen Dreiecke auf zwei Seiten antiparallel ein Dritter, mit dem er keine Gemeinsamkeiten hat. Durch seine beiden Enden sowie durch zwei Eckpunkte der dritten Seite ist es immer möglich, einen Kreis zu zeichnen.

Weitere Eigenschaften der Dreieckshöhen

Eigenschaften der Mindesthöhe eines Dreiecks

Die Mindesthöhe eines Dreiecks hat viele extreme Eigenschaften. Zum Beispiel:

Die minimale orthogonale Projektion eines Dreiecks auf Linien, die in der Ebene des Dreiecks liegen, hat eine Länge, die der kleinsten seiner Höhen entspricht.
Der minimale gerade Schnitt in der Ebene, durch den eine unflexible dreieckige Platte gezogen werden kann, muss eine Länge haben, die der kleinsten der Höhen dieser Platte entspricht.
Bei kontinuierlicher Bewegung zweier Punkte entlang des Umfangs des Dreiecks aufeinander zu, darf der maximale Abstand zwischen ihnen während der Bewegung vom ersten zum zweiten Treffen nicht kleiner sein als die Länge der kleinsten der Höhen des Dreiecks.
Die Mindesthöhe in einem Dreieck liegt immer innerhalb dieses Dreiecks.

Grundverhältnisse

h a = b sin ⁡ γ = c sin ⁡ β , (\displaystyle h_(a)=b\sin \gamma =c\sin \beta ,)
h a = 2 S a , (\displaystyle h_(a)=(\frac (2S)(a)),) Wo S (\displaystyle S)- Fläche eines Dreiecks, ein (\displaystyle a)- die Länge der Seite des Dreiecks, auf der die Höhe abgesenkt wird.
h a 2 = 1 2 (b 2 + c 2 − 1 2 (a 2 + (b 2 − c 2) 2 a 2)) (\displaystyle h_(a)^(2)=(\frac (1)(2 ))(b^(2)+c^(2)-(\frac (1)(2))(a^(2)+(\frac ((b^(2)-c^(2))^ (2))(a^(2))))))
h a = b c 2 R , (\displaystyle h_(a)=(\frac (bc)(2R)),) Wo bc (\displaystyle bc)- das Produkt der Seiten, R − (\displaystyle R-) Radius des umschriebenen Kreises
h a: h b: h c = 1 a: 1 b: 1 c = b c: a c: a b (\displaystyle h_(a):h_(b):h_(c)=(\frac (1)(a)):( \frac (1)(b)):(\frac (1)(c))=bc:ac:ab)
1 h a + 1 h b + 1 h c = 1 r (\displaystyle (\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_ (c)))=(\frac (1)(r))), Wo r (\displaystyle r) ist der Radius des eingeschriebenen Kreises.
S = 1 (1 h a + 1 h b + 1 h c) ⋅ (1 h a + 1 h b − 1 h c) ⋅ (1 h a + 1 h c − 1 h b) ⋅ (1 h b + 1 h c − 1 h a) (\displaystyle S =(\frac (1)(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_(c ))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\frac (1)(h_(c))) )(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1)(h_(b))))(\ cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_(a)))))))), Wo S (\displaystyle S)- Fläche eines Dreiecks.
a = 2 h a ⋅ (1 h a + 1 h b + 1 h c) ⋅ (1 h a + 1 h b − 1 h c) ⋅ (1 h a + 1 h c − 1 h b) ⋅ (1 h b + 1 h c − 1 h a) (\ Anzeigestil a=(\frac (2)(h_(a)(\cdot )(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b))) +(\frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\ frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1 )(h_(b))))(\cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_ (A))))))))), ein (\displaystyle a)- die Seite des Dreiecks, auf die die Höhe fällt h ein (\displaystyle h_(a)).
Die Höhe eines gleichschenkligen Dreiecks abgesenkt zur Basis: h c = 1 2 4 a 2 − c 2 , (\displaystyle h_(c)=(\frac (1)(2))(\sqrt (4a^(2)-c^(2))),)

Wo c (\displaystyle c)- Basis, ein (\displaystyle a) - Seite.

Satz über die Höhe eines rechtwinkligen Dreiecks

Wenn die Höhe in einem rechtwinkligen Dreieck A B C (\displaystyle ABC) Länge h (\displaystyle h), vom Scheitelpunkt eines rechten Winkels gezogen, teilt die Hypotenuse durch eine Länge c (\displaystyle c) in Segmente m (\displaystyle m) Und n (\displaystyle n) entsprechend den Beinen b (\displaystyle b) Und ein (\displaystyle a), dann sind die folgenden Gleichungen wahr.

Um viele geometrische Probleme zu lösen, müssen Sie die Höhe einer bestimmten Figur ermitteln. Diese Aufgaben haben angewandter Wert. Bei Bauarbeiten hilft die Höhenbestimmung bei der Berechnung erforderliche Menge Materialien und bestimmen, wie genau Neigungen und Öffnungen hergestellt werden. Um Muster zu erstellen, muss man oft eine Vorstellung von den Eigenschaften haben

Viele Menschen sind trotz guter Schulnoten beim Bauen ganz normal geometrische Formen Es stellt sich die Frage, wie man die Höhe eines Dreiecks oder Parallelogramms ermittelt. Und es ist das Schwierigste. Dies liegt daran, dass ein Dreieck spitz, stumpf, gleichschenklig oder rechtwinklig sein kann. Jeder von ihnen hat seine eigenen Konstruktions- und Berechnungsregeln.

So ermitteln Sie grafisch die Höhe eines Dreiecks, in dem alle Winkel spitz sind

Wenn alle Winkel des Dreiecks spitz sind (jeder Winkel im Dreieck beträgt weniger als 90 Grad), gehen Sie wie folgt vor, um die Höhe zu ermitteln.

Gemäß den angegebenen Parametern konstruieren wir ein Dreieck.
Lassen Sie uns die Notation einführen. A, B und C sind die Eckpunkte der Figur. Die jedem Scheitelpunkt entsprechenden Winkel sind α, β, γ. Die diesen Ecken gegenüberliegenden Seiten sind a, b, c.
Die Höhe ist die Senkrechte vom Scheitelpunkt des Winkels zur gegenüberliegenden Seite des Dreiecks. Um die Höhen eines Dreiecks zu ermitteln, konstruieren wir Senkrechte: vom Scheitelpunkt des Winkels α zur Seite a, vom Scheitelpunkt des Winkels β zur Seite b und so weiter.
Der Schnittpunkt der Höhe und der Seite a wird mit H1 bezeichnet, und die Höhe selbst wird mit h1 bezeichnet. Der Schnittpunkt von Höhe und Seite b ist H2, die Höhe h2. Für Seite c beträgt die Höhe h3 und der Schnittpunkt H3.

Höhe in einem Dreieck mit stumpfem Winkel

Überlegen Sie nun, wie Sie die Höhe eines Dreiecks (größer als 90 Grad) ermitteln können. In diesem Fall liegt die aus einem stumpfen Winkel gezeichnete Höhe innerhalb des Dreiecks. Die verbleibenden zwei Höhen liegen außerhalb des Dreiecks.

Die Winkel α und β in unserem Dreieck seien spitz und der Winkel γ stumpf. Um dann die Höhen zu konstruieren, die sich aus den Winkeln α und β ergeben, ist es notwendig, die ihnen gegenüberliegenden Seiten des Dreiecks fortzusetzen, um Senkrechte zu zeichnen.

So ermitteln Sie die Höhe eines gleichschenkligen Dreiecks

Diese Figur hat zwei gleiche Seiten und der Basis, wobei auch die Winkel an der Basis einander gleich sind. Diese Seiten- und Winkelgleichheit erleichtert die Konstruktion von Höhen und deren Berechnung.

Zeichnen wir zunächst das Dreieck selbst. Die Seiten b und c sowie die Winkel β, γ seien jeweils gleich.

Zeichnen wir nun eine Höhe vom Scheitelpunkt des Winkels α und bezeichnen sie mit h1. Denn diese Höhe ist sowohl die Winkelhalbierende als auch der Median.

Für das Fundament kann nur eine Konstruktion erstellt werden. Zeichnen Sie beispielsweise einen Median – ein Segment, das den Scheitelpunkt eines gleichschenkligen Dreiecks und die gegenüberliegende Seite, die Basis, verbindet, um die Höhe und Winkelhalbierende zu ermitteln. Und um die Länge der Höhe für die anderen beiden Seiten zu berechnen, können Sie nur eine Höhe erstellen. Um also grafisch zu bestimmen, wie die Höhe eines gleichschenkligen Dreiecks berechnet wird, reicht es aus, zwei der drei Höhen zu ermitteln.

So ermitteln Sie die Höhe eines rechtwinkligen Dreiecks

Es ist viel einfacher, die Höhen eines rechtwinkligen Dreiecks zu bestimmen als bei anderen. Dies liegt daran, dass die Beine selbst einen rechten Winkel bilden, also Höhen sind.

Um die dritte Höhe zu bilden, wird wie üblich eine Senkrechte gezeichnet, die den Scheitelpunkt des rechten Winkels und die gegenüberliegende Seite verbindet. Um in diesem Fall ein Dreieck zu bilden, ist daher nur eine Konstruktion erforderlich.